基于角度轨迹和自适应权重的改进MOEA/D算法

蒙毅 魏文红 吴帅

(东莞理工学院 计算机科学与技术学院,广东东莞 523808)

基于分解的多目标进化算法(MOEA/D, Multi-objective Evolutionary Algorithm Based on Decomposition)[1]是广泛使用的多目标优化算法,该算法能将原始多目标问题分解为一组对应不同决策偏好的标量子问题并行优化,最终实现对多目标最优化问题的求解。多目标进化算法在解决NP(Nondeterministic Polynomial)问题中具有求解速度上的优势,在许多领域中被用来解决决策和最优化问题。在工程优化中,多目标进化算法可以用于解决复杂的设计问题,如结构优化、参数优化和排队等问题[2-4]。此外,多目标进化算法还可以应用于金融领域的投资组合优化、交通规划、电力系统调度、医疗决策等领域[5],为各行各业的决策和优化问题提供实用和高效的工具。

传统的MOEA/D算法采用一组均匀的权重向量,在对应目标空间的超平面中均匀分布。理论上,在算法迭代过程中,标量子问题会向超平面收敛,从而形成分布均匀的Pareto最优解[6]。然而,对具有复杂前沿的多目标问题,不同的子问题向Pareto前沿收敛的难度也不同。若计算资源均匀分布,则易搜索区域容易出现资源饱和,Pareto最优解分布密集,而难以解决的区域则会出现资源短缺,Pareto最优解分布稀疏。因此,在存在尖峰、长尾和不连续前沿的情况下,MOEA/D求解得到的近似Pareto前沿往往分布不均匀,解集无法完全覆盖Pareto前沿。如何更快、更全面地搜索高质量种群,仍然是多目标进化算法领域需要进一步研究的问题。

近年来,针对MOEA/D算法在该问题上的缺陷,学者们针对改进权重向量分布做了许多工作。张宁等人针对不连续前沿问题提出了MOEA/D-DE-DC算法[7],该算法使用DBSCAN(Density-Based Spatial Clustering of Applications with Noise)聚类方法,将不连续前沿转化为多个连续前沿子问题。刘庆等人采用模拟退火的局部搜索方法提出了IMOEA/D[2],加强了复杂前沿的搜索能力。Dong等人提出了一种使用链式分段策略的自适应权重向量调整策略的MOEA/D-DE-CS算法[8],该算法从人口分布中导出链式结构以获得适应前沿形状的权重向量分布。此外,还出现了MOEA/D-URAW[9]、MOEA/D-STM[10]、MOEA/D-RWV[11]等调整权重的MOEA/D改进算法,但仍存在求解不稳定和时间开销大等问题。

为解决上述问题,本文提出基于角度自适应调整权重向量的MOEA/D-ATSAW(MOEA/D Based on Angle Trajectory and Self-Adaptive Weight)算法,该算法能够在迭代中判断前沿形状,并自适应地选择不同的权重向量分配策略,以提高Pareto解集的多样性。具体而言,本文提出一种基于角度的聚类方法来准确识别前沿的形状,该方法利用Pareto解的支配关系和分布特性,将欧氏距离计算转化为角度计算,以简化计算方式。为提高聚类结果准确性,采用轨迹聚类的方法,结合点集运动特征,将各个Pareto前沿分段尽可能相互连接,以保证算法求解的稳定性。最后,MOEAD-AAWV算法根据聚类-合并结果采用不同的分布策略来分配子问题计算资源,以提高求解结果的多样性。

1 基于切比雪夫分解的MOEA/D算法

MOEA/D中构造聚合函数的方法有加权求和法[12]、切比雪夫分解法[13]和基于惩罚的边界交叉法[1]等,其中切比雪夫分解法应用最为广泛。在MOEA/D中,将切比雪夫聚合函数值作为需要优化的标量子问题,可以表示为

subject tox∈Ω,

(1)

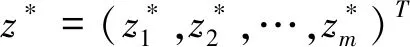
MOEA/D算法流程如下:

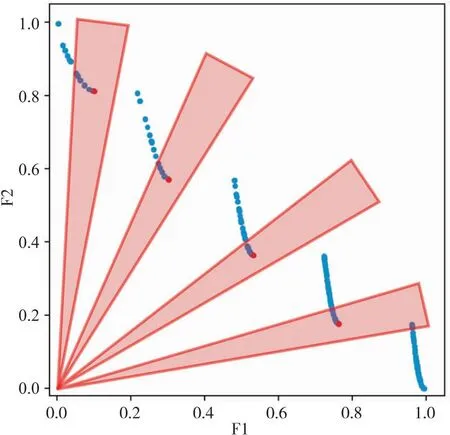
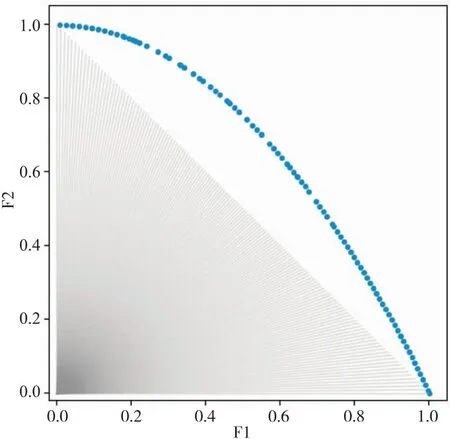
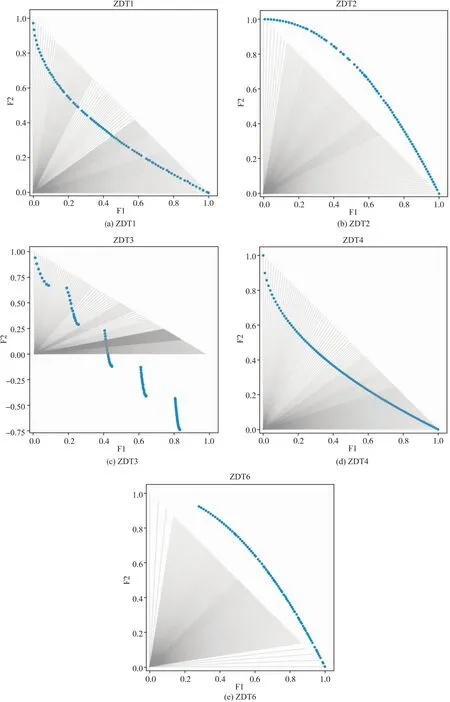
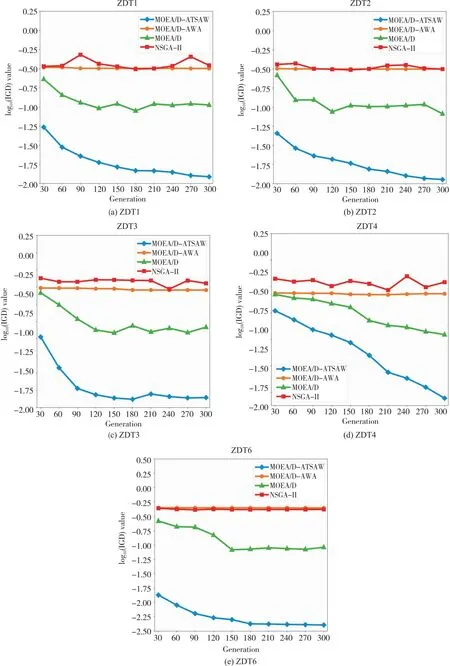
Algorithm1 MOEA/DInput:1. 多目标优化问题MOP;2. 算法停止标准:通常为最大迭代次数MAX gen;3. 种群规模:N;4. 邻居数量:T;5. N个均匀分布的权重向量:λ1,λ2,…,λN。Output: EP(算法运行中得到的非支配解)Step 1. 算法初始化:1.1. EP=Ø;1.2. 对每个i=1,2,…,N,计算所有权重向量两两之间欧氏距离,求出与λi最接近的T个权重向量,得到集合B(i)={i1,i2,…,iT}, 其中i1,2,…,T为种群的下标, λi1,λi2,…,λiT是最接近λi的T个权重向量;1.3. 初始化种群x1,x2,…,xN,并计算相应目标函数值FVi=F(xi);1.4. 计算出当前最优值(近似参考点)z=(z1,z2,…,zm)T。Step 2. 更新种群:对I=1,2,…,N重复以下操作2.1. 繁殖:随机从B(i)中选取两个下标k和l, 通过对xk和xl使用遗传操作产生新解y;2.2. 改良:根据具体问题对y使用修复或启发式,产生y′;2.3. 更新最优值z: 对每个j=1,2,…,m, 若fi(y′)>zj(最大化问题中为zj

2 DBSCAN聚类算法

DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一种基于密度的空间聚类算法,最早由Ester等人于1996年提出[14]。该算法通过指定参数距离阈值Eps和最小邻居minPts,将具有足够密度的样本点划分为一个簇,并递归地对该点邻居进行相同操作,直到所有样本点均被划分或该点邻居不满足最小邻居minPts为止,如图 1所示。该算法的优点是可以处理多种形状的簇,且无需人为指定簇的数量。DBSCAN的这种特性适合将其应用于求解未知前沿的多目标优化问题的算法,其样本点p的邻域可以被表示为

(2)

本文提出一种改进的DBSCAN算法,用于聚类Pareto前沿的带状簇。为应对Pareto前沿近似呈扇形分布的情况,该算法优化了DBSCAN的距离计算方式。如图2所示,使用样本点与坐标轴原点连线与x轴的夹角大小作为样本位置,将样本间的角度差的绝对值作为判断样本点关系的指标,而不采用计算样本点与核心点的欧氏距离的方式。通过该方法,数据维度从二维降至一维,不仅能降低聚类算法的时间复杂度,还能精准地判断前沿是否连续,从而采取相应的权重调整策略。需要注意的是,对于Pareto前沿值域不在[0,1]范围内的函数,该方法失效,因此需要对Pareto集做归一化操作。

图1 DBSCAN聚类示意图

图2 基于角度的DBSCAN聚类示意图

图3 对不连续前沿聚类示意

3 MOEA/D-ATSAW

在传统MOEA/D算法中,采用均匀分布的权重向量来优化多目标问题,每种权重分布对应一个标量优化子问题,并在空间中呈均匀超平面分布。实际上,这种权重向量分布不能很好地适应非凸前沿、尖峰长尾以及不连续前沿等问题,从而导致较差的求解效果。MEOA/D-AAWV算法则通过自适应地调整权重向量分布,以实现对解集分布稀疏区域的资源倾斜,进而优化求解结果。

3.1 前沿划分与合并

当算法第一阶段结束时,算法所求的解集已总体收敛至Pareto前沿区域,但往往解集多样性较差,且部分处于尖峰、长尾或是不连续前沿端点的极端解难以求解,导致解集在这些区域中分布稀疏。对这些区域进行重点优化,并对已知前沿通过改进的DBSCAN方法进行聚类,从当前解集中提取前沿信息,包括前沿的分布范围和区域密度等信息,如图 3所示,根据所得聚类部分数量,判断其前沿形状,对不连续前沿解集进行聚类,得到多个部分的Pareto前沿,可知其不连续,如图4。

图4 对不连续前沿聚类结果

但此方法并不总是可行的,当算法第一阶段所求得解集分布不均匀时,基于密度半径的DBSCAN算法往往会因为样本点间距离过大,样本点分布稀疏而导致一条看似总体连续的前沿被划分为多个部分,这将导致第二阶段中,权重向量被全部分配于这些区域而导致空白区域的“饥饿”现象,且由于这些前沿片段往往长度较小,在其中分布着大量权重向量会导致这些区域的“饱和”现象。

为弥补DBSCAN方法单纯依靠密度距离判断的缺陷,本文引入轨迹聚类方法[15],并结合船舶轨迹聚类思想[16],通过定义每个前沿部分中Pareto解的方向角θ和角速度ω,判断Pareto前沿所划分的每个部分前后是否连续,从而将其稀疏的前沿部分得以相对平滑地连接起来,正确分配权重向量注意力区域。因而在聚类合并中,对划分所得的每个前沿部分维持一个角速度ω=Δθ/Δd,由于只关心每个部分前后能否相连,且只需关心前一部分尾部与后一部分头部夹角关系,夹角通过式(3)计算:

(3)

(4)

前沿划分-合并流程见算法2。

Algorithm2 基于点集运动状态的轨迹合并Input:1. 聚类所得前沿划分:Clusters;2. 角度阈值:Eps。Output:mergedClustersStep1. 对每个Clusteri,i=1,2,…,k执行以下操作1.1 如newCluster为空,则将当前前沿划分加入新聚类中,转至Step 1;1.2 计算newCluster尾部变化率ωj=Δθ/Δd和Clusteri的首部夹角及其变化率ωij=Δθ/Δd;1.3 如newCluster和Clusteri的轨迹平滑,即ωij-ωj≤Eps,则将当前前沿划分加入新聚类列表中,否则将newCluster加入mergedClusters中,并将Clusteri作为新的newCluster,转至Step 1。Step 2.若newCluster不为空,则将newCluster加入mergedClus-ter中,并输出mergedCluster。

3.2 自适应分布权重向量

MOEA/D-ATSAW自适应权重流程如算法3所示,其根据前沿划分结果,将前沿分为三类:凸前沿、非凸前沿和不连续前沿。算法根据运行过程中对前沿分布进行分析,判断前沿类型,从而选择不同的调整策略使权重向量分布适应搜索情况。由于子问题与权重向量一一对应,因而在调整权重向量后,还需对子问题与相邻子问题进行调整[7]。

Algorithm3自适应分布权重向量Input:1. 当前外部人口:EP;2. 聚类参数:Eps, minPts。Output:newVectorsStep 1. 对EP归一化处理Step 2. 根据EP计算前沿数量2.1 对EP进行聚类,其阈值为Eps, 最小邻居为minPts,获得前沿分段EP_clusters;2.2 对EP_clusters执行Algorithm2,合并分段得到merged-Clusters。Step 3. 判断mergedClusters中分段数量,若等于1则为连续前沿,执行Step 4,否则执行Step 5Step 4. 若为连续前沿,执行以下操作4.1 根据凸函数定义判断前沿形状,若为凸函数则采用均匀分布数量权重,若为非凸则采用不均匀分布;4.2 将EP按区域划分,判断各区域数量;4.3 根据各区域Pareto解所占种群比例,乘以数量权重系数得到新的区域分配数量;4.4 重新分配各区域的权重向量,得到newVectors。Step 5. 若为不连续前沿,执行以下操作5.1 计算各前沿分段的长度;5.2 根据各分段所占总长度的比例与Pareto解所占种群比例分配权重向量,得到newVectors。Step 6. 重新调整邻居B(i)={i1,i2,…,iT},i=1,2,…,NStep 7. 重新调整种群,对每个权重向量λ1,λ2,…,λN分配其切比雪夫值最小的个体〛

由于非凸前沿不存在尖峰和长尾，只需维持总体的均匀分布，可在局部稀疏部分做微小调整，如图5所示。而凸前沿由于存在尖峰和长尾现象，这两个区域的子问题分布较少，难以在狭长区域中获得均匀的Pareto分布。因此，需要采用特殊的策略使权重向量的分布由均匀转向两端稠密、中间相对稀疏。在MOEA/D-ATSAW算法中，采用开口朝上的抛物线函数做比例映射实现该策略。该函数具有定义域两端梯度较大、中间部分梯度较小的特性，可以使权重向量较多地集中在尖峰和长尾区域，即搜索区域的高低两侧。分区数为10的情况如图6所示，其中心区域子问题较为稀疏，第一阶段的搜索已使中心区域子问题密集，由于MOEA/D的精英策略，后期改变权重向量分布不会导致Pareto解丢失，而尖峰长尾区域则会因为子问题的增多而分布更密集。

图5 均匀分布权重向量

图6 不均匀分布权重向量

图7 MOEA/D-ATSAW在ZDT测试函数上的近似Pareto前沿及其映射后的权重向量分布

图8 算法迭代过程中IGD数值

对于不连续的Pareto前沿，MOEA/D-ATSAW采用与雷达相似的思想，加上一定误差范围(本文中取Eps)的区域进行加权向量的分配，而不存在Pareto解分布的区域将不会被分配权重向量，这样可以避免子问题资源被浪费在空白区域的无用搜索中，亦能优化已有前沿的分布。而前沿部分±Eps扩大前沿部分的搜索区域，尽可能保证Pareto前沿被完整搜索，即使存在多个不连续前沿仅能搜索到一个Pareto解的极端情况，MOEA/D-ATSAW也可以经过多次调整扩大其搜索范围，有更高的几率搜索到完整前沿，提高搜索性能。此外，对某些搜索难度较大的连续前沿，往往会因初期搜索结果不理想而被误判为不连续前沿，因而使用此方法不断扩大各个部分的搜索范围，结合聚类-合并策略，可以使MOEA/D-ATSAW能在第二阶段搜索中合并成为连续前沿。

4 实验与分析

为验证MOEA/D-ATSAW自适应权重向量对优化尖峰、长尾及不连续前沿优化等问题求解结果的有效性，选取广泛使用的多目标测试函数ZDT1、ZDT2、ZDT3、ZDT4和ZDT6[17]进行实验分析，选择同类改进的自适应权重向量算法MOEA/D-AAWN[18]、MOEA/D-AWA[19]、MOEA/D-M2M[20]与不调整权重向量的基于切比雪夫分解法的多目标优化算法MOEA/D[1]，与最具代表性的基于Pareto支配关系和拥挤距离排序的多目标遗传算法NSGA-II[21]作对比。运用广泛使用的反向世代距离IGD作为性能指标定量分析算法性能。

4.1 性能指标

使用在多目标优化问题研究中应用最为广泛的反向世代距离IGD(Inverted Generational Distance)[22]作为评价指标来评估算法求解结果的收敛性和多样性。假设解集PF*为从真实Pareto前沿均匀采样的一组解，PF为真实Pareto前沿，则反向世代距离IGD可以被表示为

(5)

4.2 参数设置

为排除其他因素对算法求解效果的影响，在参与实验的所有算法中，均采用模拟二进制交叉算子(SBX)[23]和多项式变异算子(PM)[24]产生子代，其中交叉概率为CR=1.0，多项式变异概率为MR=1.0，交叉和变异参数设置为Nc=20，Nm=20。种群规模N=150，相邻子问题数量T=15，最大迭代次数MAXgen=300，其余参数与其原文一致。

4.3 实验结果与分析

实验结果表明，MOEA/D-ATSAW在优化权重向量分布的改进算法中，不论测试函数的前沿分布连续或不连续，相较其他算法均有性能提升，各算法IGD数据如表1所示。从表1的结果可以看出，对测试函数ZDT1、ZDT2、ZDT3、ZDT4和ZDT6，MOEA/D-ATSAW具有最佳性能表现。特别地，对于测试函数ZDT3的不连续前沿，MOEA/D-ATSAW算法体现出其优越性，IGD指标显著降低。相比未调整权重向量分布的算法，该算法在优化多目标问题上具有明显的优势。

表1 各算法IGD指标均值(方差)

MOEA/D-ATSAW在ZDT测试集上所得Pareto前沿及其映射后的权重向量分布如图 7所示，其权重向量取最后一次调整的分布。算法计算EP中各部分前沿的稀疏程度后，为不同密度的前沿分段分配权重向量，在解分布较少的部分权重向量分布相对稠密，而解分布密集的部分减少权重向量的分配，仅留下部分作为优化Pareto解分布之用。

5 结语

针对多目标优化问题中求解难度较高的复杂前沿和不连续前沿问题，提出一种基于MOEA/D算法的新型算法——MOEA/D-ATSAW，增加了一种新的聚类-合并Pareto前沿划分方法，不同于以往计算样本点欧氏距离的做法，本文根据Pareto解的分布特征，采用基于几何角度的方式计算样本点之间的距离，相比较于传统方法，该方法的性能开销更小且更精准。此外，本文结合轨迹聚类中的方法，类似于船舶轨迹聚类，赋予样本点运动学特征，根据Pareto前沿分段的分布特性和平滑特征，使其尽可能地合并为一条总体平滑、连续的Pareto前沿，这种聚类-合并方法所产生的Pareto分段为下一步的权重向量调整策略奠定良好基础。

同时，还提出了新的自适应多策略权重向量调整机制，它根据Pareto前沿划分所得分段，并根据前沿的分段数量、分段长度、分段中解的数量及分布特征判断前沿类型和形状，再自适应地采取不同分配策略，针对各个前沿分段或划分区域，分配不同数量和密度的方向向量，同时根据切比雪夫分解法的几何特性，将其映射到权重向量。通过这种方法倾斜子问题搜索资源以适应不同前沿类型，获得更好的Pareto前沿分布。通过相邻子问题调整和种群重分配，将每个子问题对应到更优的权重向量，即切比雪夫函数值更小的权重向量上，维持算法在调整之后的稳定性。

MOEA/D-ATSAW在ZDT测试函数上的实验结果表明，在相同的参数和遗传操作下，MOEA/D-ATSAW不仅性能和求解效率优于其他算法，且权重向量经过调整后并未造成求解结果的剧烈波动，其性能指标曲线平滑稳定，证明了本文改进的Pareto前沿聚类划分方法和多策略权重向量调整机制的有效性。后续研究计划将MOEA/D-ATSAW算法进一步扩展到高维多目标问题上，利用基于角度的优势降低对高维多目标问题的前沿评估难度，以求更低复杂度地计算前沿信息，为自适应方法提供环境信息，从而更好调整参数，加快算法收敛速度。