一种求解结构组合优化问题的BB型算法

李凯 林彭壮汉 胡子健 程万友

(东莞理工学院 计算机科学与技术学院,广东东莞 523808)

考虑以下无约束优化问题:

(1)

(2)

(3)

近年来压缩感知和稀疏优化不断发展,为了求解问题(3)式,人们提出了不同的求解方法,其中常见迭代阈值算法ISTA[4]算法,因其内存需求低、迭代简单的特点,常用于求解大规模问题。为了加速ISTA[4]算法的收敛速度,Beck和Teboulle[5]提出了快速迭代收缩阈值算法(FISTA)。Wright[6]等人提出了可分离近似的稀疏重构算法(SpaRSA),该方法使用带保障的BB步长和非单调线搜索,算法的数值结果很好,适用于实际问题。此外求解问题(2)和(3)的算法还有乘子交替方向法SALSA[7]、内点法[8]、梯度投影法[9]、近端梯度方法[2]等。

本文第1节将提出一种求解问题(3)的BB型算法,并分析算法的收敛性。在第2节,通过数值实验与一些现有的算法进行比较,证明了所提出算法的有效性。

1 算法描述

在本文中,使用Huang[10]等人提出新的BB步长来求解稀疏优化问题。在一些假设下,证明了所提出算法的全局收敛性。算法的迭代格式如下:

xk+1=xk+βkdk,

其中dk是搜索方向,βk∈(0,1]是步长参数。由于目标函数φ(x)是非光滑的,因此搜索方向不能使用负梯度方向,根据函数φ(x)的近似函数的极小值点来确定如下搜索方向:

dk=Pro(xk)-xk,

(4)

其中Pro(xk)是以下问题的极小值点:

其中(αk)-1I是函数f(x)的Hessian矩阵∇2f(xk)的近似,uk=xk-αk∇f(xk)。显然,函数Q(z,xk)可以看成是函数φ(x)在xk处的二次近似。由于函数Q(z,xk)是强凸函数,因此问题(5)式有唯一最小值点:

αk的选取会直接影响算法的效率,BB型算法以其快速收敛和较低的计算复杂度而受到广泛关注,Barzilai和Borwein[11]提出了以下长和短的步长选择:

其中sk-1=xk-xk-1,yk-1=∇f(xk)-∇f(xk-1)。在所提出的算法中使用了Huang[10]等人提出一种新的步长,其具体表达式如下:

其中

由于自适应步长策略的成功应用[12],使用自适应步长

(6)

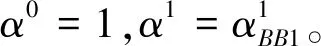
其中γ>1,这种可变设置使得步长策略在一些应用中能够得到显著的性能改进。为了避免步长太小或者太大,结合(6)式,使用带保障的BB步长

(7)

其中0<αmin<αmax<∞,αmin,αmax为固定的参数。

Fletcher在文献[13]中指出,BB方法的一个重要特征是其固有的非单调性,通常采用一些非单调线搜索来获得好的数值性能。因此,采用文献[14]中提出的非单调线搜索策略,若步长βk满足不等式

(8)

则βk是可接受的步长,其中σ∈(0,1),Ck具有以下迭代形式:

(9)

参照文献[14]中的设置,令C0=φ(x0),Q0=1,η∈(0,1)。下面给出求解问题(3)的非单调BB型算法。

算法1非单调BB型算法

2)若满足算法的终止条件,则结束算法。否则,转步骤3)。

3)根据(4)式计算搜索方向dk。

4)计算mk是使得βk=ρmk满足不等式(8)的最小整数,令xk+1=xk+βkdk。

5) 由(9)式计算Ck+1和Qk+1。

6) 由(7)式计算新的步长αk+1。

7) 令k:=k+1,转步骤2)。

备注:对于步骤4的非单调线搜索,文献[14]中指出Ck+1是Ck和φ(xk+1)的凸组合。因为C0=φ(x0),因此可以得出Ck是函数φ(x0),φ(x1),…,φ(xk)的凸组合,对于所有的k,有φ(xk)≤Ck,η的选择控制了非单调性的程度。

1.1 收敛性分析

设问题(3)式中的目标函数满足以下假设:

假设1

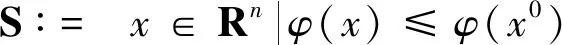
2)在水平集S上,存在一个邻域N,使得函数f(x)是连续可微的光滑函数,且f(x)的梯度满足Lipschitz连续性。也就是说,存在常数L>0,使得

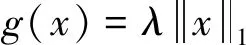
0∈∂φ(x*)=∇f(x*)+∂g(x*),

则x*是问题(3)的稳定点。当f(x)为凸函数时,φ(x)也是凸函数,则满足条件的点x*是问题(3)的全局解。不难证明,对于任意给定的αk>0,若

为了证明算法的收敛性,首先介绍一些支撑主要证明的引理。参照文献[6]中引理2和引理3的证明, 可以得到如下结果。

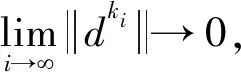
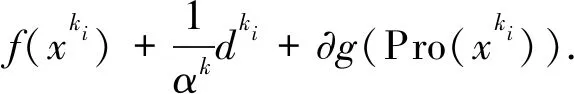
通过取极限i→∞,使用∂g的闭性和αk的有界性,有0∈∇f(x*)+∂g(x*)=∂φ(x*)成立。这与x*不是稳定点相矛盾,因此证毕。

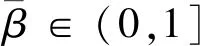
(10)

且dk是下降方向。若βk满足不等式(10),则

(11)

(12)

由∇f(x)的Lipschitz连续性和(12)式可知

φ(xk+βkdk)-φ(xk)=

(13)

因Pro(xk)=xk+dk是函数Q(z,xk)的唯一最小值,所以根据函数Q(z,xk)的定义(4)式有

Q(xk+dk,xk)=

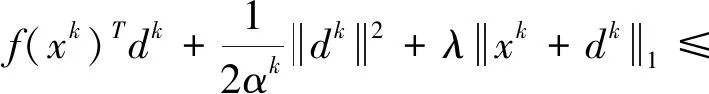
(14)

由(14)式得

(15)

在非单调线搜索过程中,对于任意的k,有φ(xk)≤Ck,结合(13)和(15)式可得

φ(xk+βkdk)-Ck≤φ(xk+βkdk)-φ(xk)≤

(16)

所以当

下面的定理表明当目标函数φ(x)是凸函数时,算法1收敛到问题(3)的全局解。

定理1设假设1成立,φ(x)有下界,序列{xk}由算法1所产生,则其任意聚点都是问题(3)式的稳定点。

证明因为 0<η<1,由(9)式和Q0=1可得

(17)

结合(9)、(10)和(17)式可得

(18)

因此{Ck}是非增的。因为φ(x)是有下界,所以{Ck}也是有下界的,所以对(18)式累加求和得

因为C0-Ck+1是有限的,所以

(19)

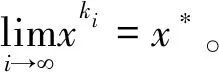
2 数值实验

在本节中,通过数值实验来研究所提出算法的数值性能,并与一些现有算法进行了比较。所有的数值实验都是由 MATLAB R2020a 编写的,并搭载在windows10 系统的 PC 上运行 (CPU:i5-7200U 2.50 GHz;内存:8.00 GB)。

(20)

所有测试算法的初始点设置为x0=0，测试问题的终止条件为

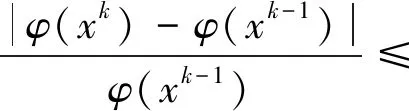
(21)

表1 λ=1/m，=10-4的比较结果

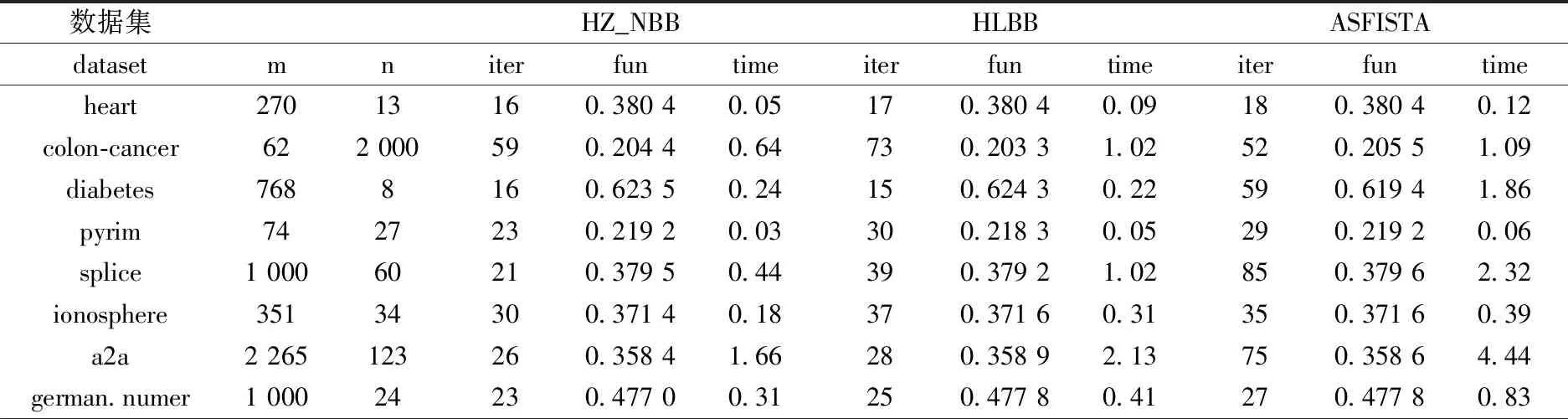
表1 λ=1/m，=10-4的比较结果

数据集HZ_NBBHLBBASFISTAdatasetmniterfuntimeiterfuntimeiterfuntimeheart27013160.380 40.05170.380 40.09180.380 40.12colon-cancer622 000590.204 40.64730.203 31.02520.205 51.09diabetes7688160.623 50.24150.624 30.22590.619 41.86pyrim7427230.219 20.03300.218 30.05290.219 20.06splice1 00060210.379 50.44390.379 21.02850.379 62.32ionosphere35134300.371 40.18370.371 60.31350.371 60.39a2a2 265123260.358 41.66280.358 92.13750.358 64.44german.numer1 00024230.477 00.31250.477 80.41270.477 80.83

(续表)

表2 λ=1/m，=10-6的比较结果

表2 λ=1/m，=10-6的比较结果

数据集HZ_NBBHLBBASFISTAdatasetmnIterfuntimeiterfuntimeiterfuntimeheart27013290.380 30.09300.380 30.13310.380 30.19colon-cancer622 000850.200 71.05900.200 51.251090.200 51.68diabetes7688770.609 90.981700.609 91.812190.609 94.30pyrim7427410.218 30.06430.218 30.09510.218 30.12splice1 00060510.372 81.01590.372 91.231730.372 83.55ionosphere35134550.370 40.33650.370 40.61720.370 41.08a2a2 2651231340.353 39.661620.353 511.342110.353 615.57german.numer1 00024400.476 70.66510.476 70.77600.476 71.48australian69014530.336 70.53640.336 70.881100.336 71.11triazines18660620.128 80.24420.128 80.19400.128 80.28svmguide31 24321940.504 21.94960.504 42.181650.504 15.96fourclass862260.533 70.0970.533 70.11180.537 70.25breast-cancer68310280.010 30.25300.010 30.35330.010 30.75sonar208601010.472 70.481330.472 40.641440.472 70.91

表3 λ=5×10-4，=10-4的比较结果

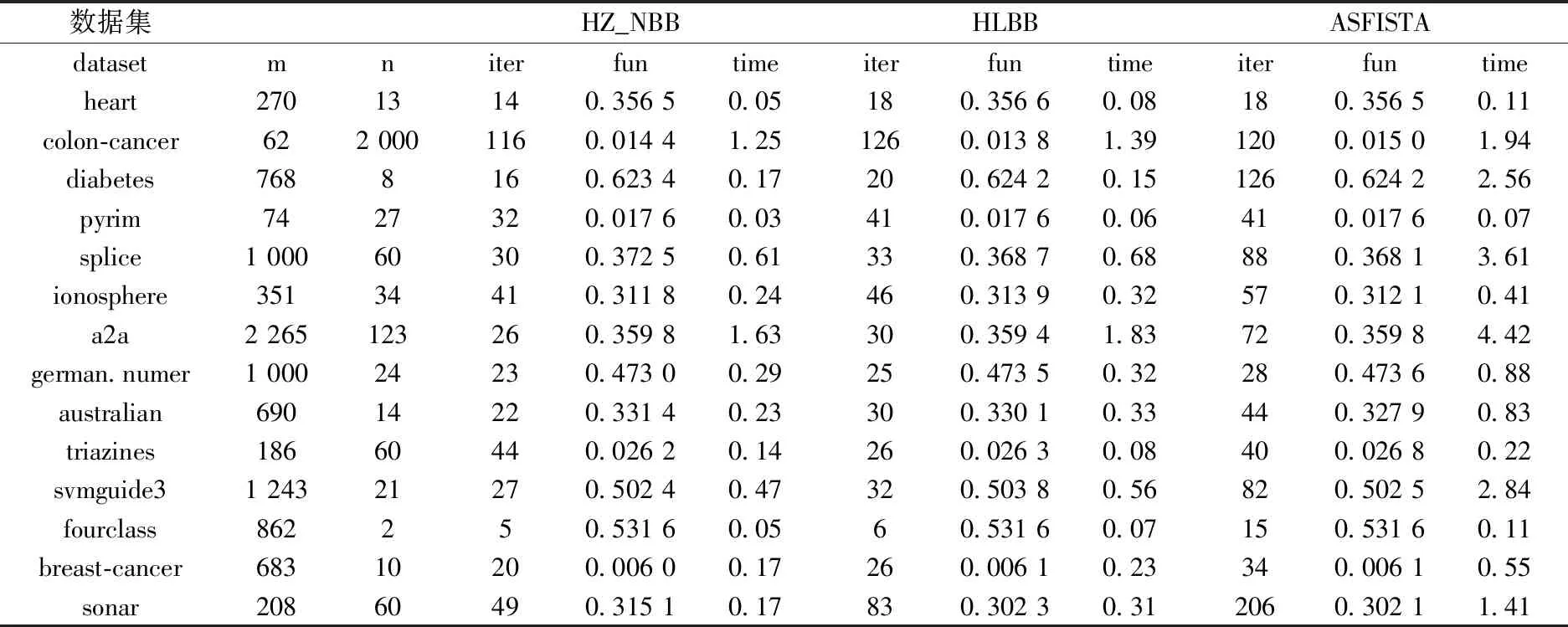
表3 λ=5×10-4，=10-4的比较结果

数据集HZ_NBBHLBBASFISTAdatasetmniterfuntimeiterfuntimeiterfuntimeheart27013140.356 50.05180.356 60.08180.356 50.11colon-cancer622 0001160.014 41.251260.013 81.391200.015 01.94diabetes7688160.623 40.17200.624 20.151260.624 22.56pyrim7427320.017 60.03410.017 60.06410.017 60.07splice1 00060300.372 50.61330.368 70.68880.368 13.61ionosphere35134410.311 80.24460.313 90.32570.312 10.41a2a2 265123260.359 81.63300.359 41.83720.359 84.42german.numer1 00024230.473 00.29250.473 50.32280.473 60.88australian69014220.331 40.23300.330 10.33440.327 90.83triazines18660440.026 20.14260.026 30.08400.026 80.22svmguide31 24321270.502 40.47320.503 80.56820.502 52.84fourclass862250.531 60.0560.531 60.07150.531 60.11breast-cancer68310200.006 00.17260.006 10.23340.006 10.55sonar20860490.315 10.17830.302 30.312060.302 11.41

表4 λ=5×10-4，=10-6的比较结果

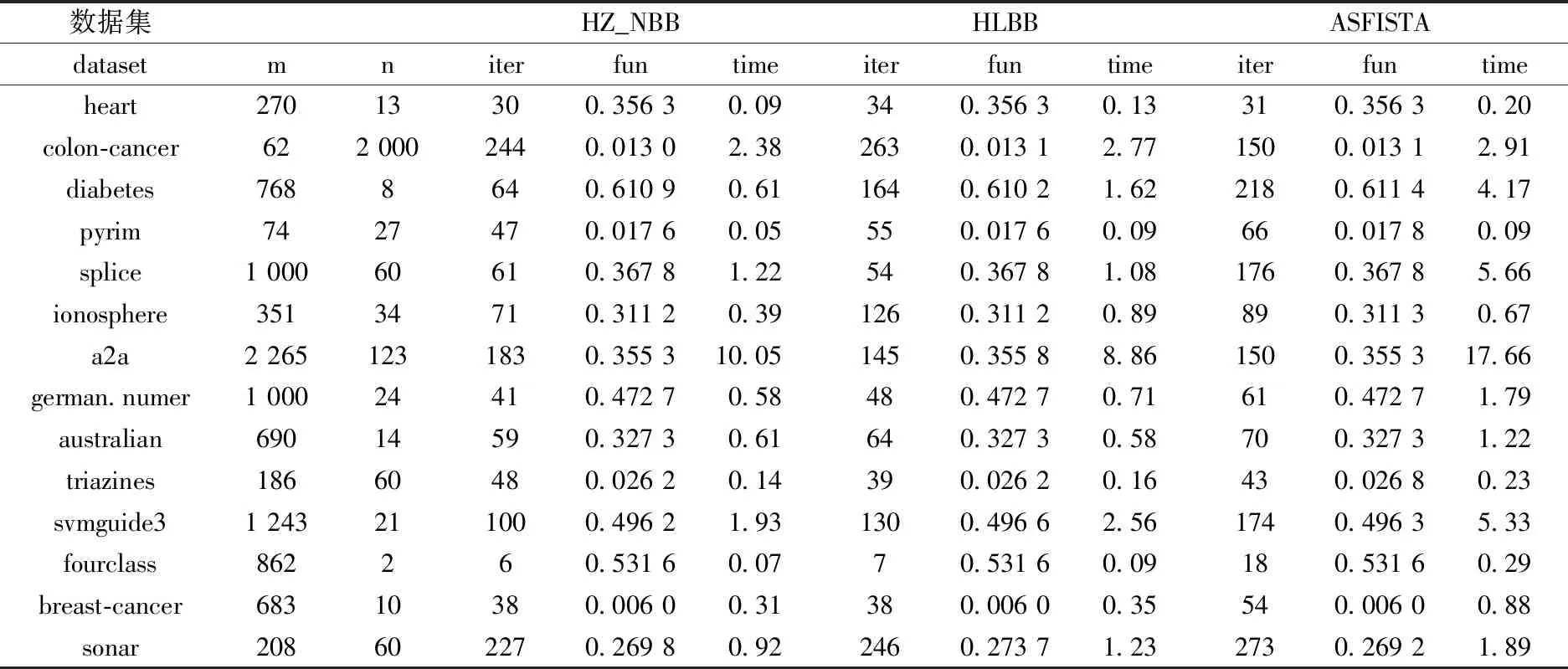
表4 λ=5×10-4，=10-6的比较结果

数据集HZ_NBBHLBBASFISTAdatasetmniterfuntimeiterfuntimeiterfuntimeheart27013300.356 30.09340.356 30.13310.356 30.20colon-cancer622 0002440.013 02.382630.013 12.771500.013 12.91diabetes7688640.610 90.611640.610 21.622180.611 44.17pyrim7427470.017 60.05550.017 60.09660.017 80.09splice1 00060610.367 81.22540.367 81.081760.367 85.66ionosphere35134710.311 20.391260.311 20.89890.311 30.67a2a2 2651231830.355 310.051450.355 88.861500.355 317.66german.numer1 00024410.472 70.58480.472 70.71610.472 71.79australian69014590.327 30.61640.327 30.58700.327 31.22triazines18660480.026 20.14390.026 20.16430.026 80.23svmguide31 243211000.496 21.931300.496 62.561740.496 35.33fourclass862260.531 60.0770.531 60.09180.531 60.29breast-cancer68310380.006 00.31380.006 00.35540.006 00.88sonar208602270.269 80.922460.273 71.232730.269 21.89

2.2 图像去模糊问题

在本小节中，测试了图像去模糊问题，测试问题具有以下形式：

其中A=RW，R表示模糊算子矩阵，W表示反正交Haar小波变换，x为原始图像，y表示模糊的观测图。类似于文献[9]中的图像反卷积实验，考虑了表5中的三个标准的基准问题，测试图像是256×256像素的Cameraman图像(如表6所示)和512×512像素的Lena图像(如表7所示)，并将HZ_NBB算法与SpaRSA[6]、AM_GPSR[17]和CPGA[2]算法进行比较。AM_GPSR是一种基于动量加速的梯度投影算法，CPGA则是一种控制步长的临近梯度算法。三个实验的正则化参数λ分别取 0.01、0.25和0.5。我们使用PSNR(峰值信噪比)来比较算法的图像去模糊性能，所有测试算法的停止条件使用(21)式，我们令=10-5。

表5 图像去模糊实验

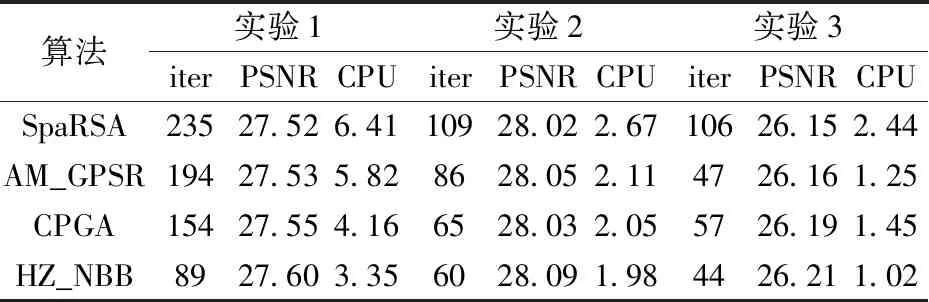
表6 Cameraman图像结果

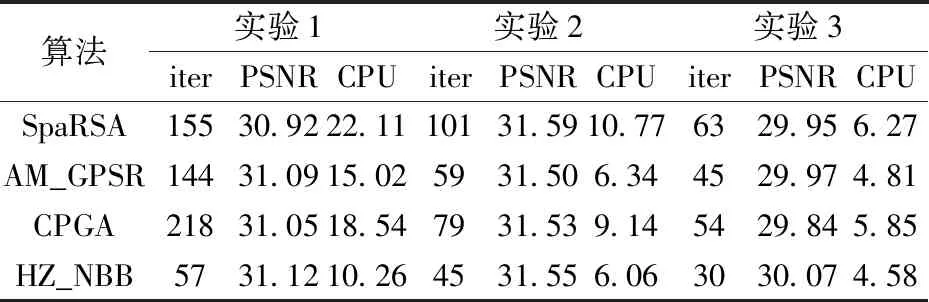
表7 Lena图像结果

表6和表7给出了所有测试问题的数值结果，从表6可以看到，对于Cameraman图像，HZ_NBB算法解决所有问题的CPU时间和迭代次数都是最少的，并且HZ_NBB算法比SpaRSA、AM_GPSR和CPGA算法获得了更好的PSNR值。从表7可以看到，对于Lena 图像，HZ_NBB算法对于所有问题的CPU时间和迭代次数都是最少的，对于实验1和3，HZ_NBB得到了最大的PSNR值，而实验2，SpaRSA得到了最大的PSNR值，图1和图2分别给出了对表5中实验1的图像去模糊结果。数值结果表明，所提出的算法是有效的。

图1 表5中问题1的Cameraman图像去模糊结果

图2 表5中问题1的Lena图像去模糊结果

3 结语

在本文中，使用一种新的BB步长结合非单调线搜索技术，提出了一种用于求解结构组合优化问题的BB型方法，在适当的条件下，证明了所提出算法的全局收敛性。在第2节中，将所提出的算法应用于1正则化逻辑回归问题和图像去模糊问题中，并与其他算法进行了数值比较，结果表明，相比于已有的算法，本文的算法使用了更少的CPU时间以及更少的迭代次数，数值性能上是更有优的。