考虑变荷载与非达西渗流的软土一维非线性固结分析
2024-02-21曹文贵崔鹏陆李慧鑫李兆帅
胡 闽,曹文贵,崔鹏陆,徐 赞,李慧鑫,李兆帅
(湖南大学 土木工程学院,长沙 410082)
0 引 言
土体固结与土体变形和强度直接相关,土体的非线性固结是目前研究的热点。传统的非线性固结都需要通过测量土体的初始有效应力对土体的固结过程进行分析,且无法解决土体初始有效应力为0对其孔隙比造成的奇异性影响,同时,土体的固结还会受到非达西渗流[1-4]的影响。因此,考虑土体中的非达西渗流与土体非线性压缩模型来解决以上问题有很重要的理论与工程意义。
多年来,土的一维非线性固结理论的研究已取得较大进展[5-9]。其中,Davis等[5]提出了孔隙比e与有效应力σ′的关系,在有效应力和固结系数沿土的深度不变的假定下给出了土体一维非线性固结的解析解。Xie 等[6-7]基于Davis 等[5]的假定考虑了变荷载,先后分析了单层和双层地基的一维非线性固结。Barden等[8]给出了一维非线性固结有限差分解。Mesri[9]等提出了经典半对数关系,即e-lgσ′与e-lgkv(kv为土体渗透系数)关系,并得到了广泛的应用。近期,Li等[10]依据试验数据提出了e-lgav(av为土体压缩系数)这一土体非线性压缩模型,Li等[10]基于该压缩模型推导的非线性固结方程及其渐近解对软土正常固结过程中的土体孔隙水压力进行了修正,减少了理论计算与试验之间的偏差。同时,该关系式在描述土体的非线性固结过程中不仅无需测量初始有效应力,而且解决了传统的e-lgσ′非线性关系在初始有效应力为0时对孔隙比造成的奇异性影响。吴思思等[11]基于Li等[10]提出的非线性压缩模型对变荷载下土体的一维非线性固结进行了分析,详细讨论了影响土体固结过程的因素,但其并未考虑非达西渗流和变荷载对土体固结过程的影响。
实际上,在软土地基中,非达西渗流更加符合土体渗流情况。已有研究表明,软土中的渗流会偏离达西定律[1-3]。谢海澜等[4]研究表明,非达西渗流相较于达西渗流,土体固结到同一固结度的时间明显增长。目前,考虑非达西渗流的软土一维非线性固结已取得诸多进展。刘忠玉等[12]、 纠永志等[13]在土体非线性变形的基础上,分别考虑了非达西渗流及土体自重应力,对饱和黏土和Terzaghi的一维固结理论进行了修正。李传勋等[14-16]基于Mesri[9]等提出的关系考虑了非达西渗流,对变荷载作用、软土的结构性以及应力历史对土体固结的影响进行了一系列的分析。但是以上研究均不可避免地需要测量土体的初始有效应力,在工程中应用不便。
综上所述,本文从Li等[10]提出的e-lgav一维非线性压缩模型和e-lgkv渗透模型出发,对正常固结的软土考虑了变荷载作用与非达西渗流对土体固结的影响,推导出了土体的一维非线性固结方程,并通过有限差分法得到该固结模型的解答。随后验证了本文解答的正确性,最后对土体的固结性状进行了详细分析。
1 固结模型的建立
本文采用应用较广的Hansbo非达西渗流模型,其v-i关系曲线如图1所示,其中:v为渗透流速;i为水力坡降;i1为Hansbo渗流中的临界水力坡降;i0为起始水力坡降;k为Hansho渗流中指数段的渗透系数;K为Hansho渗流中线性段的渗透系数;m为模型参数。地基固结模型如图2所示,其中:H为地基厚度;av0为土体初始压缩系数;kv0为土体初始渗透系数;z为土体深度。

图1 非达西定律的v-i关系曲线Fig.1 Curve of v-i in non-Darcy law

图2 地基固结模型Fig.2 Foundation consolidation model
式(1)为变荷载表达式,当时间t
(1)
式中:q0和qu分别为初始荷载和最终荷载;t0为荷载加载完成的时间。
Li等[10]提出的非线性压缩模型和传统的非线性渗透模型分别为:
(2)
(3)
式中:e和e0分别表示土体的孔隙比和初始孔隙比;av和kv分别表示土体的压缩系数和渗透系数;C和Ck分别为土体的压缩指数和渗透指数,且C和Ck分别是土体e-lgav压缩曲线的斜率和土体e-lgkv渗透曲线的斜率。
由压缩指数定义[17]可得
(4)
由式(2)和式(4)可得孔隙比与有效应力的关系为
(5)
式中σ0′表示初始有效应力。
将式(5)代入式(3)可得渗透系数与有效应力的关系,即
(6)
土体单元体积应变ε为[17]
(7)
Hansbo[18]提出的非达西定律为
(8)
当i (9) 式中:u为超静孔隙水压力;γw为水的重度。 由式(8)和式(9)可以得出 (10) 由式(10)可得土体单元体积渗流变化[5]为 (11) 假定土体单元渗流等于土体单元体积变化[19]可得 (12) 有效应力原理为 σ′=σ0′+q(t)-u。 (13) 结合式(2)、式(6) 、式(13)可得固结系数的表达式为: (14) (15) 式中Cv0是初始固结系数。其表达式为 (16) 将式(5)、式(6)、式(13)代入式(12)中可推导出考虑变荷载作用和非达西渗流的土体一维非线性固结方程,即 (18) 同理,i≥i1时土体的一维非线性固结方程为 (19) 2种情况下的固结方程求解的初始条件与边界条件为 (20) 引入无量纲参数:U=u/qu,Z=z/H,Tv=Cv0t/H2,Tv0=Cv0t0/H2,Q=q(t)/qu,Q0=q0/qu。 将无量纲参数代入式(19)中,i (21) (23) (24) 本文的固结方程式(19)很难求出其解析解,因此采用有限差分法对本文的固结方程进行求解。在Z-Tv平面划分差分网格,b和j分别表示空间和时间节点,b=0,1,2,…,l;j=0,1,2,…,n。b=0和b=l分别表示土层顶部和底部的位置,j=0和j=n分别表示初始时刻和最终时刻。Δz表示空间步长,取步长0.01,Δt表示时间步长,取步长0.000 01。将式(21)差分可得 (25) 其中: (26) (27) (28) 其中: (29) (30) 无量纲化后相应的初始条件和边界条件为 (31) 这样,式(25)与无量纲化后的初始条件和边界条件构成了封闭的代数方程组,因此可以利用差分法对U进行求解。按孔压定义的平均固结度Up为 (32) 可推出 (33) 按变形定义的平均固结度Us为 (34) 可推出 (35) 式中ef为最终孔隙比。 土体的沉降变形S为 (36) 可推出 将李冰河等[19-20]提出的半解析法与本文利用差分法所得的数据进行对比,以验证本文差分数据的正确性。 李冰河等[19]基于达西定律提出的半解析法,因此,需采用本文m=1时的特殊情况与李冰河等[19]的半解析法进行对比,并采用表1中给出的土体参数作为计算参数取值。图3(a)分析了不同Tv下随深度变化的超静孔隙水压力。可以看出,取相同参数时,半解析法与本文所采用的差分法所得出的数据完全重合。从而验证了本文差分法的正确性。 表1 Li等[10] 试验测得的土体参数Table 1 Soil parameters measured in Li’s experiment [10] 图3 本文解与李冰河解对比Fig.3 Comparison between the solution of the present study and Li Binghe’s solution 采用表2土体参数作为计算参数取值,与李冰河等[20]的沉降解答进行对比,本文解答仍取m=1的特殊情况。如图3(b)所示,施加荷载为骤加荷载时,本文解答与初始有效应力σ0′为100 kPa时的李冰河等[20]解答基本重合,该对比也验证了本文解的正确性。 表2 固结性状分析所采用的土体参数[21]Table 2 Soil parameters used for consolidation behavior analysis[21] 基于以上验证结果的正确,现以顶面透水及底面不透水地基模型为例,分析非达西参数m和i1、加载速率以及初始压缩系数av0和压缩指数与渗透指数的比值C/Ck对土体固结过程的影响。外荷载取用单级等速加载的形式,所需土体计算参数如表2所示。 已有研究表明[4],非达西渗流相比于达西渗流会对土体的固结有明显的滞后效应。而这种滞后效应与本文中非达西参数m和i1有关。如图4所示,随着m和i1的增大,Tv=0.4时土体相同深度的超静孔隙水压力会越大,这说明m和i1的增大,会导致土体中超静孔隙水压力消散越慢。 图4 非达西参数m和i1对超静孔隙水压力的影响Fig.4 Influence of non-Darcy parameters m and i1 on excess pore water pressure 图5表明,随非达西参数m和i1的增大,非达西渗流的平均固结度Us会越加偏离达西渗流情况下的平均固结度Us,如图5(a)所示,具体表现为m和i1越大,土体中超静孔隙水压力消散越慢,导致土体沉降速率越慢。这表明非达西渗流是土体沉降发展过程中不可忽略的因素之一。如图5(b)所示,Tv=0.6时,m=1.25,i1=2.5参数下的非达西渗流的平均固结度Us为72%,达西渗流的平均固结度Us为82%,两者偏差达到10%。需要说明的是,m和i1的变化并不会影响土体的最终沉降量,但m和i1的变化会影响土体的沉降速率。原因在于:根据式(36),地基的最终沉降量只与初始孔隙比和最终孔隙比相关。 图5 非达西参数m和i1对平均固结度Us和地基沉降变形S的影响Fig.5 Influence of non-Darcy parameters m and i1 on average consolidation degree Us and foundation settlement deformation S 经过分析,非达西参数m和i1的增大会导致平均固结度Up的固结速率变慢。图6为Us和Up对比。两者规律相同,但Up始终要慢于Us,即沉降的发展始终要快于孔压的消散,这与谢康和等[22]阐述的观点一致。 图6 Us和Up对比Fig.6 Comparison between Us and Up 固定非达西参数m=1.25及i1=2.5。采用表2 中的土体参数分析了初始压缩系数av0对平均固结度Us和地基沉降变形S的影响,如图7所示。 图7(a)反映出av0会影响平均固结度Us的发展,具体表现为av0越大,土体的沉降越快。而且av0会影响土体的最终沉降量,如图7(b)所示,av0越小,土体的最终沉降量越小。 图8分析了不同压缩指数与渗透指数的比值下平均固结度Us和地基沉降变形S的变化曲线。仇超等[23]的研究表明,压缩指数C与渗透指数Ck都会影响到土的沉降过程。渗透指数Ck越小,土体的渗透性就越弱,因此就导致土体的沉降速率会更慢;压缩指数C越小,会导致土体的沉降速率越快。固定参数m=1.25及i1=2.5,qu取值100 kPa。图8表明,C/Ck的比值越大,土体的沉降速率会越慢。这与仇超等[24]的结论一致。同时,C/Ck值的变化不会引起最终沉降量的变化。 图8 不同C/Ck值下平均固结度Us和地基沉降变形S关于Tv的关系曲线Fig.8 Relation curves of average degree of consolidation Us and foundation settlement deformation S with respect to Tv under different C/Ck values 采用表2中的土体参数,固定非达西参数m=1.25及i1=2.5,qu取值100 kPa,对变荷载下不同加载速率下的土体沉降进行了分析,如图9所示。可以看出Tv0的减小会导致荷载的加载速率变快,进而导致沉降速率加快。此外,加载速率的变化不会导致最终沉降量的改变。 图9 不同加载速率下土体的沉降曲线Fig.9 Curves of soil settlement under different loading rates 4.4.1 二级加载 图10(a)为各加载形式荷载变化示意图。图10(b)反映了图10(a)中不同加载形式下土体的沉降趋势。固定非达西参数m=1.25及i1=2.5,固定土体参数av0=1.222×10-3kPa-1,C/Ck=0.5以及最终荷载qu=100 kPa。单级等速加载完成时间为Tv2=0.1。二级中第一级加载时间为Tv=0至Tv1=0.05,加载到q1=50 kPa;第二级加载时间为Tv2=0.55至Tv3=0.6;从q1=50 kPa加载到qu=100 kPa。如图10(a)所示。从图10(b)中可以看出3种加载形式最终沉降量一致,其中骤加荷载下的土体沉降速率最快;单级等速加载次之,二级加载最慢。如Tv2=0.55时,骤加荷载下土体沉降量为12.3 cm;单机加载下土体沉降量为11.9 cm;二级加载下土体沉降量为6.4 cm。在实际工程中,外界因素的影响如改动设计、天气恶劣等原因会导致停工,地基上的加载更加符合二级加载形式或多级加载形式[24],此时若直接简化为恒载或单级加载形式,会一定程度高估其固结速率。 图10 不同加载形式下土体沉降曲线Fig.10 Curves of soil settlement under different loading modes 4.4.2 预 压 对于一些特殊的工程而言,比如公路的建设,通常会对土体进行预压处理,进而减小路面施工后土体的沉降变形。预压方式通常有3种,即等载预压、欠载预压以及超载预压。3种预压的加载情况和使用参数如图11(a)和图11(b)所示,最终荷载qu=100 kPa。加载的完成时间为Tv1=0.1,预压的完成时间Tv2=0.75。欠载预压q1=80 kPa,超载预压q2=120 kPa。需要说明的是,在该分析中假定卸载预压荷载和增加路面浇筑荷载均为瞬间完成。3种不同预压方案的沉降如图11(b)所示,可以看出预压方案的不同会导致土体的沉降过程也不相同。在预压完成时,超载预压产生沉降最大。因此,在需要预压的工程中, 应首选超载预压的方式。 图11 不同预压情况下土体沉降曲线Fig.11 Curves of soil settlement under different preloading conditions (1)与已有模型相比,本文所采用的模型无需测量土体的初始有效应力,只需测量土体初始压缩系数,可更加方便地应用于工程中。 (2)土体固结过程中的非达西渗流的影响不容忽视。非达西渗流参数m和i1越大,土中超静孔隙水压力消散越慢,土体固结越慢。特别地,当m>1.25且i1>0.8时,非达西情况相对于达西情况沉降固结度的偏差最大已超过10%。 (3)初始压缩系数av0越小,C/Ck值越大,土体的沉降速率越慢;av0越小,土体的最终沉降量也会越小。 (4)土体的沉降速率与外荷载的加载速率、外荷载形式相关。外荷载加载速率越快,土体沉降速率越快。实际工程中要考虑加载形式的影响,若直接简化为恒载或单级加载形式,会一定程度高估其固结速率。2 固结模型的求解
3 实例分析与验证



4 固结性状分析
4.1 非达西参数对土体沉降的影响

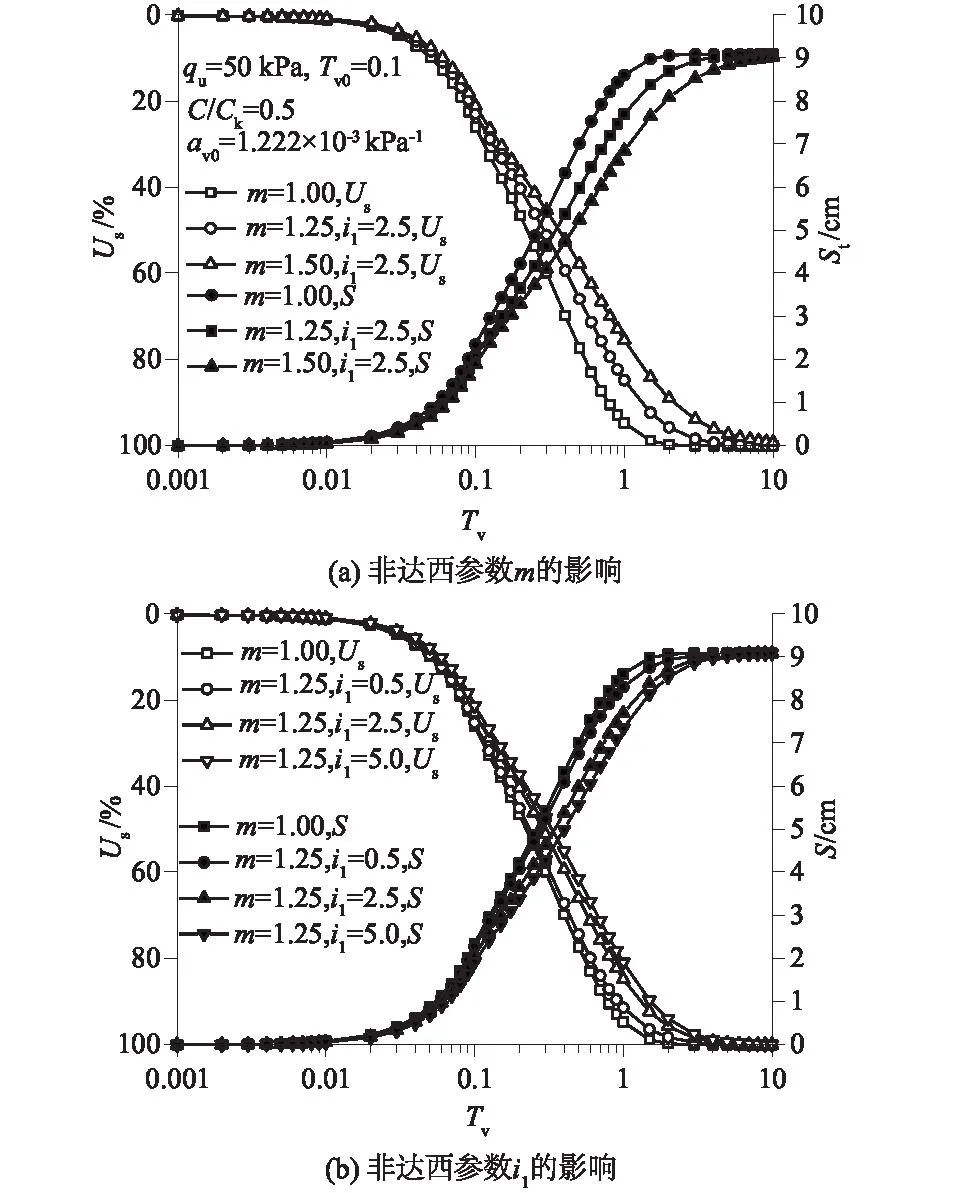
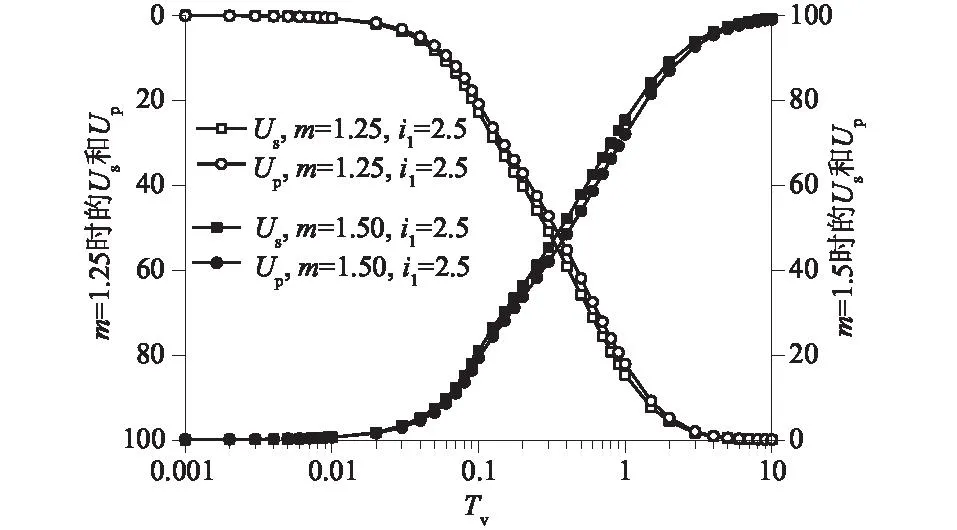
4.2 初始压缩系数和压缩指数与渗透指数的比值对土体沉降的影响

4.3 加载速率对土体沉降的影响
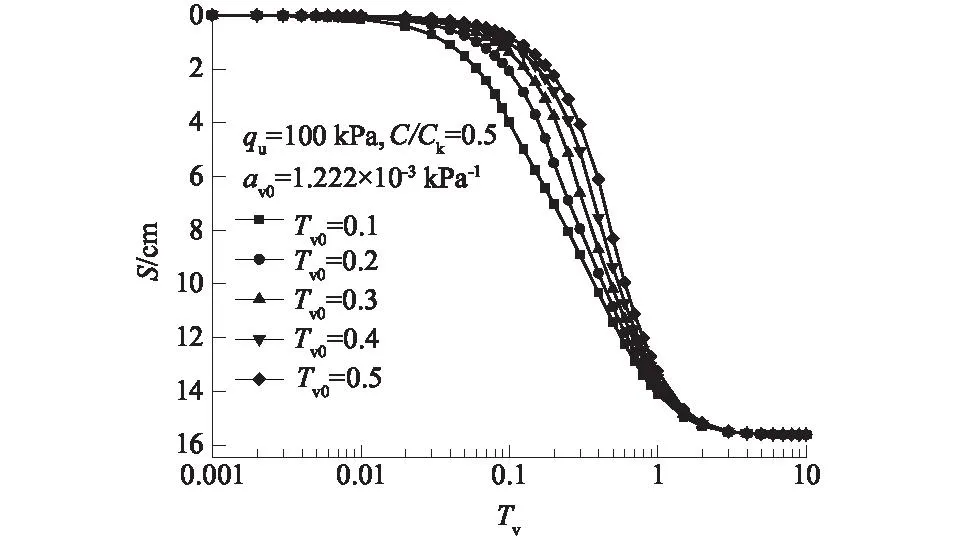
4.4 加载形式对土体沉降的影响
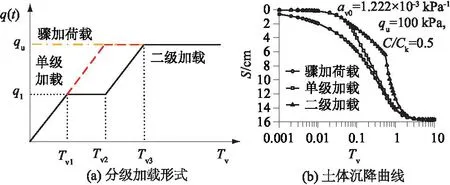

5 结 论
