内河溢油污染源逆时追踪数值模拟

付 玉,童思陈,2,王 啸,蒋聘凤,黄国鲜

(1.重庆交通大学 河海学院,重庆 400074; 2.国家内河航道整治工程技术研究中心,重庆 400074; 3.河南省交通规划设计研究院有限公司,郑州 450000; 4.中国环境科学研究院,北京 100012)

0 引 言

随着我国水路运输蓬勃发展,内河船舶运输成为推动经济增长的重要力量[1]。由于内河航道相对狭窄,船舶海损事故时有发生,或导致石油、燃油泄漏,对水域环境造成污染。自20世纪60年代以来,溢油研究多针对海洋区域,且主要关于溢油正向扩展漂移模拟。孙兰君等[2]基于蒙特卡罗方法及Mia散射理论建立了溢油海水双分布函数模型,为海洋激光遥感测油提供了理论基础;Wang等[3]基于“粒子法”开发了包含海洋环境预测的近海溢油预测系统;Simecek-Beatty等[4]结合空间验证的技巧评分法进行了石油泄漏预测,研究了海上溢油预测的全新方式。近年来,通过对河道中溢油现象的研究,学者们发现与海洋环境不同,油粒子在扩散过程中更容易受河岸和河底的固壁作用影响[5],主要受水流对流作用控制。Gautama等[6]将合成孔径雷达(Synthetic Aperture Radar,SAR)遥感技术应用于河道溢油模型的验证;蒋文燕[7]在二维模型基础上,考虑增加垂向尺度油滴扩散和上浮作用对垂向油滴浓度分布的影响,建立了河道三维溢油数学模型;黄瑞等[8]将改进油粒子模型应用于长江镇扬段上,分析了溢油扩散特征和油膜厚度变化,并考虑了溢油风化及岸边吸附等影响;Jacketti等[9]拓展了开源地下石油模拟器(Subsurface Oil Simulator,SOSim)用于预测河流底部缓慢移动的石油轨迹。

相对于溢油污染正向预测和预报,针对污染事件反向追踪溢油源的研究较为缺乏。辛小康等[10]采用优化算法建立了河流水污染事故污染源识别模型;杨海东等[11]结合MCMC(Markov Chain Monte Carlo)和微分进化方法提出河流突发性水污染的溯源方法; Soong等[12]使用随机行走粒子跟踪算法模拟油粒子聚集物在河流中的输移特性并开发了FluOil模型。大多数学者将污染追溯问题看作源项反演问题,采用概率法或模拟优化法等反演污染源的位置和历史运动轨迹。国内外开发的具有污染源上游回溯功能的模型有RiverSpill溢油模型和OILMAP数值模拟系统,其中RiverSpill更适用于河流污染情况,但其使用的是一维流场计算方法[13],OILMAP具有二维及三维计算能力,多用于模拟溢油与岸线、海床等的相互作用[14]。除此以外,目前针对内河溢油污染源的逆时追踪研究很少,关于多维度模拟狭长河道复杂地形的溯源追踪有待进一步研究深化。本文在平面二维水流数值模拟基础上,基于Fortran语言从底层自主开发了溢油污染源逆时追踪模型,可实现溢油污染过程的逆向运算,反演溢油的漂移路径和寻找溢油污染源的位置。通过在三峡库区典型河段的溢油污染源逆时追踪数值模拟,可较好地模拟寻找出溢油污染源,可对溢油污染事故的应急处置和污染源的确定提供支撑。

1 模型及求解

内河具有河宽较窄、水深较浅、平面形态复杂等特点,河道溢油主要受水流流速控制,对流作用突出。溢油污染数学模型是在水流数学模型基础上建立的,本文采用的二维水流数学模型基于课题组前期研究成果[15]。计算采用贴体正交曲线网格,差分方程采用三对角矩阵算法求解,数值模拟采用SIMPLEC算法,并使用欠松弛技术促进非线性迭代的收敛。

在溢油应急时间尺度下[16],基于拉格朗日方法建立了溢油扩展漂移油粒子模型,将油膜离散为1 000颗(可根据需要自行设置)直径为10～1 000 μm的球形油粒子,油膜的扩散和漂移被视为多个油粒子在外部驱动力作用下的叠加效应。油粒子模型可以综合流场和河岸地形的影响,适用于模拟水文条件较为复杂的河流中的溢油事故。本文重点研究瞬时溢油导致的短期环境影响,在此期间溢油的运动主要为自身的扩展和漂移运动,重力和黏性力起主导作用[17]。

1.1 溢油正向扩展漂移模型

1.1.1 扩展过程

根据FAY理论,扩展主要分3个阶段:重力-惯性力扩展阶段、重力-黏性力扩展阶段和表面张力-黏性力扩展阶段[18]。本文主要考虑在重力和黏性力作用下的油膜扩展情况,即采用Mackay修正的FAY理论重力-黏性力公式计算油膜的扩展,即

(1)

V0=πR02h0。

(2)

式中:A为油膜表面积(m2);t为时间(s);K0为油膜面积增长率;V0为溢油体积(m3);R0为油膜半径(cm);h0为油膜初始厚度(cm)。

1.1.2 漂移过程

溢油发生后,油膜自身会做扩展运动,还会在水流、波浪和风等外界动力的驱动下漂移扩散。漂移过程包括平移过程和随机扩散过程。在平移过程中,对于库区河道水流,影响漂移的主要动力因素是水流和风,油粒子的平移速度可由式(3)计算,即

vp=vf+avw。

(3)

式中:vp为油粒子平移速度(m/s);vf为水流速度(m/s);a为风力因子,一般取0.03～0.04;vw为水面以上10 m处风速(m/s)。扩散过程中,油粒子在水中的运动是具有随机性的湍流弥散过程。本文采用生成随机数的方法来计算油粒子可能扩散距离,表达式为

(4)

式中:S0为扩散距离(m);R为利用函数生成的[-1,1] 区间内的均匀分布的随机数;D0为水平方向上的扩散系数;Δt为时间步长(s)。

1.1.3 油粒子的单步距离

一个时间步长内单颗油粒子的单步距离St计算方法为

St=vpΔt+S0=(vf+avw)Δt+S0。

(5)

1.1.4 油粒子的流速插值

水流数学模型计算过程中,采用了贴体正交曲线网格,首先可得到每个网格节点的流速。在二维欧拉法水流数学模型基础上,采用拉格朗日法把每个油粒子视作独立的模拟对象进行模拟反演,其原理如图1所示。在水动力模块计算中只能得到每个网格节点流速,而每颗油粒子的位置是随机的,因此可先根据面积相等法编程,对油粒子进行搜索定位,找出每颗油粒子所在网格中的位置。比如,假定经搜索,确定某颗油粒子O(x,y)在某个网格A1A2A3A4之中(如图1所示)。

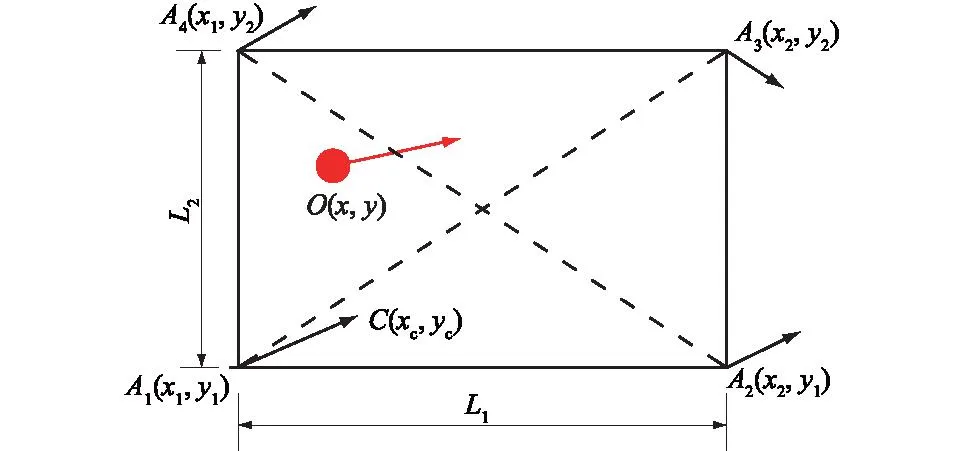
图1 油粒子流速插值原理Fig.1 Schematic of oil particle velocity interpolation

各网格节点的坐标如图1,网格中心点的坐标为C(xc,yc)。设各网格节点坐标分别为A1(x1,y1)、A2(x2,y1)、A3(x2,y2)、A4(x1,y2),计算网格边长分别为L1、L2,设坐标变换函数为

(6)

式中:x、y是原始坐标系中油粒子O的坐标;ξ、η是经过坐标变换后油粒子O在贴体正交曲线坐标系中的坐标。

式中ξi、ηi是网格上各顶点Ai的局部坐标。插值函数f(xi)为

(8)

于是,由二维水流数学模型计算可得出每个网格节点A1、A2、A3、A4的流速vx、vy,利用式(6)—式(8)即可插值得出该颗油粒子O(x,y)的流速vxO、vyO。

1.2 溢油污染源逆时追踪模型

1.2.1 实现思路

(1)首先,获取溢油污染发生时刻末的污染范围和面积,并确定时刻末溢油油品和油粒子位置。

(2)进行平面二维水动力数值模拟并获取每个网格节点的水动力参数。

(3)自时刻末起,对每颗油粒子进行逆时追踪反演计算,模拟油粒子反方向的漂移轨迹,从而确定溢油污染源,具体实现步骤:①对油粒子进行逆时追踪运算,每颗油粒子前一时刻位置坐标为

(9)

式中:X0和Y0为油粒子当前时刻的位置坐标;X和Y为油粒子前一时刻的位置坐标;dt为时间步长;vx0和vy0分别为x和y方向的水流流速;vwx和vwy分别为x和y方向的风速;S0x和S0y分别为油粒子在一个步长时间内x和y方向的扩散距离。

②计算所追踪油粒子区域面积,若所得面积大小满足污染源判别标准,则将此区域作为溢油污染源;若不满足,则重新进行计算。追踪过程如图2所示。

图2 溢油污染源逆时追踪示意图Fig.2 Inverse time tracking of oil spill pollution source

1.2.2 判别标准

1.2.2.1 油膜面积的计算

由油粒子模型可知,油膜可视为大量油粒子组成的云团,即油粒子群。其面积可采用任意多边形面积公式进行计算,即

(10)

其中,每时刻最外层的油粒子坐标分别为A1(x1,y1)、A2(x2,y2)、…、An(xn,yn)。

1.2.2.2 污染源判定

根据溢油的正向扩展漂移运动特征可知,在反向追踪溢油源头的过程中,将会显示溢油面积逐渐缩小且油粒子逐渐聚拢的过程,在模型中可预设一个油膜厚度阈值dmax。研究表明当油膜厚度为1 mm时,溢油在水中的扩展过程将停止[19],因此可初步设定dmax=1 mm。再根据油膜厚度反算油膜面积Smin,当某时刻溢油污染面积S≤Smin时,则可认为已寻找到溢油污染源。

2 模型验证

三峡库区变动回水区洛碛段船舶易发生海损事故,溢油风险较大,因此将洛碛段作为典型河段进行模拟。

2.1 水流模型验证

利用2015年5月28日实测的水位和流速对二维水流模型进行了验证(图3),实测流量为6 180 m3/s。可见,水位、流速计算值与实测值均符合良好。

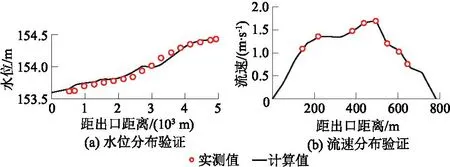
图3 水位、流速分布验证Fig.3 Validation of water level and flow velocity

2.2 溢油正向扩展漂移模型验证

课题组开展了溢油扩展漂移的概化水槽试验[20],采用其中一组工况对溢油数学模型进行了验证(图4、图5)。其中,水流速度v为0.25 m/s,溢油量m为31.0 g。可知,油膜面积、厚度模拟值与试验值均吻合良好,偏差在±15%之内。

图4 溢油扩展漂移模拟与室内试验过程比较Fig.4 Comparison of oil spill spread and drift between simulation and indoor test

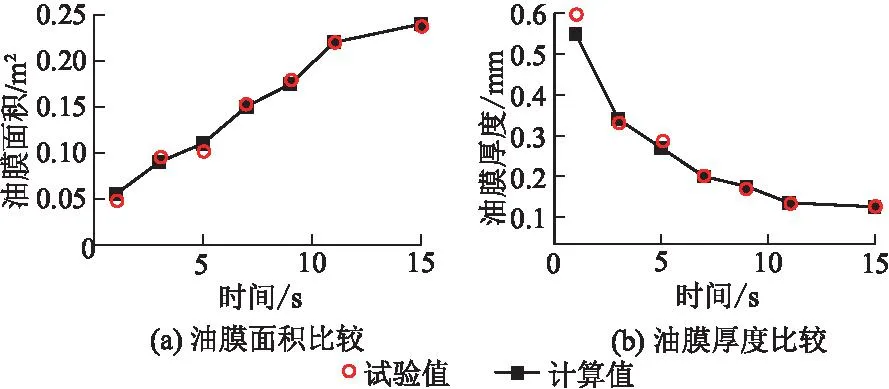
图5 溢油数学模型与室内试验油膜面积与厚度的比较Fig.5 Comparison of area and thickness of oil film between mathematical modelling and indoor test

3 溢油逆时追踪模拟

3.1 流场模拟

采用洛碛段为典型河段,模拟计算范围长度约5.1 km,宽度约1.0 km。选取洪水期流量为22 000 m3/s,尾水位为170.22 m。经分析,该河段中洪水期与平水期流量为6 180 m3/s的河道条件并无明显差别,因此借鉴了前文率定的糙率。

3.2 污染源追踪模拟

设油品为润滑油,扩散系数D0=3.0×10-4,溢油量为1 000 kg,溢油密度为940.5 kg/m3,风速为1.5 m/s。时刻末(溢油发现时刻)油膜面积为70 440 m2,油粒子颗粒数设为1 000,计算时间步长为10 s。模拟可得到溢油污染源逆时追踪过程如图6所示,相应各典型时刻的溢油追踪过程特征参数如表1所示。

表1 不同追踪时刻溢油油膜面积和厚度特征统计Table 1 Areas and thicknesses of oil spill film at different moments

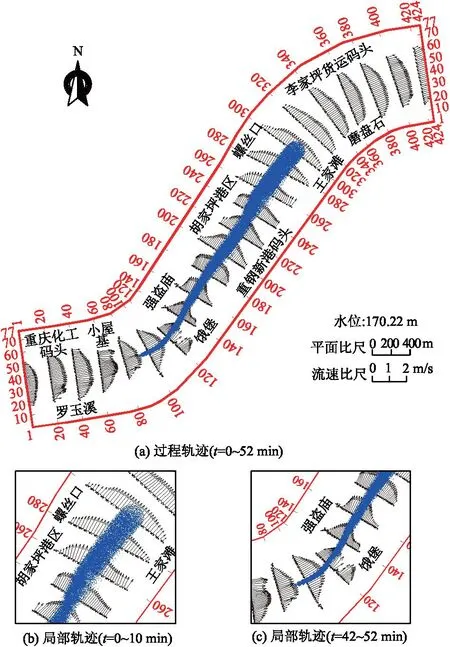
注:数字表示沿边界方向分布的网格线数量。图6 模拟的溢油逆时追踪过程轨迹及局部轨迹Fig.6 Local trajectories of inverse time tracking simulation

溢油源油膜厚度阈值dmax=1 mm,反算得到预设油膜面积Smin=1 063.26 m2。当模拟得到油膜面积S

3.3 溢油事故应急处置建议

溢油事故发生后,或将严重危害河流水体环境、水中动植物、河岸滩涂及沿岸的人类生产生活,若能及时寻找溢油事故源头,可为溢油事故应急处置提供有效指导。一旦发现河道溢油事故,应立即启动应急响应机制,根据溢油泄漏量、发生地点、河流流量等划分事故风险等级,制定相应的溢油处理方案。可选择水流流速较小或支流交汇口等位置作为溢油围控点[21],及时布设围油栏或拦污浮筒,在取水口和自然保护区等敏感水域设置多层油栅[22],或采用浮标、阻隔膜和重力锚组成的软隔离设施,便于隔离和收集漂浮污染物与可溶或沉积污染物[23],减小油膜的扩散范围。当流速较大时,可使用高速撇油器回收油污,然后利用吸附剂或化学清洁剂对河面进行清理。此外,也可采用原位燃烧法[24]、表面清洗剂[25]、分散剂[26]和生物修复[27]等方法修复含油污水。

4 结 论

在溢油应急时间尺度范围内,基于平面二维水流数学模型,采用Fortran语言从底层开发建立了溢油污染扩展漂移及污染源逆时追踪模型。在水流数学模型和溢油扩展漂移数学模型验证基础上,考虑了内河水动力对流作用突出的特点,选取了三峡库区洛碛河段作为典型河段进行了溢油污染源的模拟反演。结果表明,各油粒子之间距离逐渐减小,油粒子逐渐聚拢。能够反演重现溢油污染物随水流的漂移扩散过程,通过预设油膜面积阈值可判断出污染源位置。

溢油模型具有逆推功能,可以把其应用在内河船舶溢油事件的航政调查决策。根据特定地点所观察到的油污情况逆推溢油的可能来源,可为不明溢油源污染事故调查提供参考,以便及时提出事故处理预案,防止油污的进一步扩散,减小溢油污染对河流环境造成的不良影响。