水电站水库库容特性解析与建模研究
2024-02-21贾本军汤正阳张海荣任家朋
贾本军,汤正阳, 2,曹 辉,郭 乐,张海荣,任家朋
(1.中国长江电力股份有限公司 智慧长江与水电科学湖北省重点实验室,湖北 宜昌 443133; 2.华中科技大学土木与水利工程学院,湖北 宜昌 430074; 3.中国三峡武汉科创园 工业控制系统科技创新中心,武汉 430070)
0 引 言
水库容积特性(又称库容特性)是水库的基本特性之一[1],狭义上,指水库水位与库容之间的关系,广义上,指水库特征变量(水位、水面面积等)与库容之间的关系。水库的库容特性有两种:一是静水库容特性,即水库坝前水位与静库容之间的映射关系;二是动水库容特性,即水库坝前水位与动库容(等于楔形库容和静库容之和)之间的映射关系。一般情况下,依据水库静水库容特性进行水库发电调度计算能够满足实际需求。因此,本文主要针对水库的静水库容特性开展研究。
在水库发电调度模型构建与求解过程中,水库库容特性的描述方式对模型求解、出力计算和算法开发均有较大影响。对于水库库容特性,既可以直接采用实测的库容-水位离散数据点对其进行描述(即列表式描述或离散化描述),也可以采用一条曲线或一个函数对其进行描述(即解析式描述或函数化描述)。水库库容特性函数化表征的关键在于导出与水库库容特性的数学性质匹配的通用性函数模型。
一般情况下,水库库容特性离散化表征可以满足水库运行调度计算的需求,目前大多研究工作[2-5]都采用这种方法。但离散化表征方法存在两方面的问题[1]:一方面,采用离散化表征方法会导致调度模型求解过程存在高频次插值计算,而使模型求解效率偏低,与之相反,由于函数计算显著快于插值计算,水库库容特性的函数化描述必然会提升各类算法(尤其是迭代类算法)求解调度模型的效率,如采用动态规划算法求解水布垭水库发电调度模型时(水位离散精度为0.05 m),离散化表征和函数化表征对应的模型求解耗时分别为1 075.6 s和586.5 s;另一方面,与通用性智能算法比较,基于调度模型数学性质的解析优化算法通常具有性能更稳定、效率更高的优点,但水库库容特性的离散化表征通常使调度模型难以被数学解析,不利于基于发电调度模型凹凸特性的解析优化算法的提出。
为避免水库库容特性离散化表征导致调度模型求解效率低、无法数学解析的难题,在模型构建、算法开发等相关研究工作中,研究者通常针对具体的研究对象,采用经验与试错相结合的方法确定用于描述水库库容特性的函数模型。例如,陈森林等[6]采用三次多项式函数描述水库库容特性,构建了水库中长期发电优化调度的解析函数模型,并提出了基于逐步优化算法的解析优化方法;Zhao等[7]采用三参数幂函数表征水库库容特性,在分析水库发电调度模型凹凸特性的基础上,提出了求解模型的逐次改进动态规划算法;Zhang等[8]采用两参数幂函数刻画水库库容特性,提出了水库调度规则的解析式推求方法。综上所述,各研究者采用了不同类型的函数来描述水库的库容特性,即水库库容特性的函数化表征缺乏统一性。一方面,这种“各自为政”的局面使各类基于调度模型凹凸特性的解析优化求解方法的可靠性、统一性和普适性难以得到保证,不利于相关研究成果的迭代改进和推广应用。另一方面,这些研究都是直接采用某种函数,然后通过拟合的方式确定函数参数,而尚未明确回答这种函数是否有效且通用的问题,即是否与水库库容特性的数学性质匹配、是否具有明确物理意义以及是否广泛适用于不同水库等。因此,有必要在前述研究工作的基础上进一步开展水库库容特性解析与建模研究,探寻一种适用性广、可靠性高、物理意义明确的水库库容特性表征函数。
目前,国内鲜有关于水库库容特性的函数化表征方面的成果报道,已有研究大多聚焦于软件工具在水位-库容曲线拟合中的应用,如王小旭[9]、席元珍等[10]、杨德祥[11]、邹响林[12]和尚宪锋等[13]利用Excel软件、Origin软件分析计算水位-库容曲线。在国外,关于这方面的研究也较少,主要的研究成果包括,Liebe等[14]在假设水库为倒三棱锥的基础上,根据三棱锥的体积公式推求出水库水深与库容之间的映射关系为两参数幂函数,即水库库容V正比于水深d的3次方(V∝d3);Mohammadzadeh-Habili等[15]利用自然对数函数与库容水位关系之间的相似性,推求了水库水深与库容之间的函数关系,即
V=Vm{exp[(ln2)d/dm] -1}N。
(1)

综上所述,已有关于水库库容特性的研究仍然缺乏系统性、完整性,尚未明确提出具有适用性广、可靠性高、物理意义明晰的水库库容特性表征函数,亟需进一步开展水库库容特性解析与建模研究。为此,本文首先解析了水库库容特性的数学性质,然后构建了描述水库形态特征的几何抽象模型,并根据该抽象模型导出了参数具有明确物理意义的水库库容特性表征函数,最后运用导出的水库库容特性表征函数拟合水库的实测库容-水位离散数据点,并基于此计算函数的拟合优度指标,从拟合优度的角度验证了所提水库库容特性表征函数的适用性和可靠性。
1 水库库容特性的数学性质
根据水库的形态特征,水库库容特性具有如下2种性质:①水库蓄水量越大,水库水位越高。②水库蓄水量越大,水库水面面积越大。一般而言,在河道上修建的水库,其库容特性都具有以上2种性质,本文所讨论的对象也仅限于具有此类特性的水库。从数学解析的角度,根据水库库容特性的两点数学性质,可以获得以下表达式,即
式中:V为水库库容;Z为水库水位;S为水库水面面积,V、Z、S均为>0的变量;f为表征水库库容特性的函数,即Z=f(V),可称之为水库库容特性表征函数。
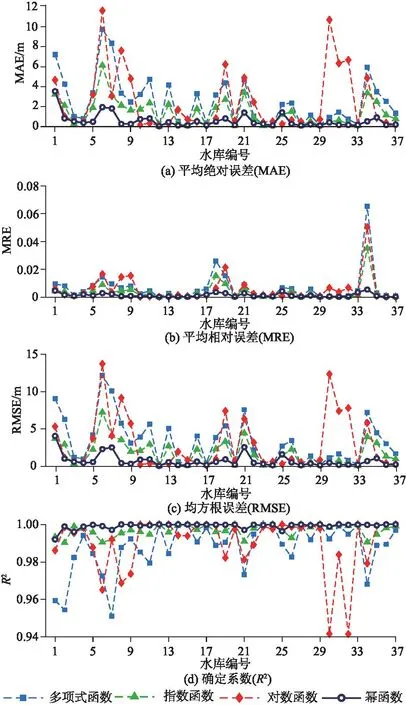
由式(1)可知,水库库容特性表征函数f(V)应满足0 f′(V)>0 ;f″(V)<0 。 (3) 式中:f′(V)为一阶导数;f″(V)为二阶导数。 式(2)、式(3)反映了水库库容特性,可以作为评价水库库容特性表征函数的标准之一。比如,当f1和f2两种函数都能够很好地拟合水库的实测库容-水位离散数据点,且拟合优度指标相等或差距很小时,可以进一步根据f1和f2两种函数的数学性质是否满足式(3)来判断f1和f2的优劣。 构建了描述水库形态特征的三棱锥模型和不规则锥体模型,在此基础上推导了水库库容特性表征函数的数学表达式,并分析了该函数的数学性质,给出了该函数的参数取值范围。 为获得水库库容特性表征函数的数学表达式,一般有2种方法:①根据经验,直接假设为某种数学表达式,如N次多项式、其他初等函数等;②根据水库的形态特征,构建几何抽象模型,在此基础上采用数学微分、积分等方法推求出水库库容特性表征函数的表达式。由于第一种方法经验性强,缺乏机理性,本文采用第二种方法。不失一般性,假设水库的形态为锥体,构建水库的几何抽象模型,如图1所示。 图1 水库的三棱锥模型和不规则锥体模型Fig.1 Triangular pyramid model and irregular cone model of reservoir 图1展示了水库的2种锥体模型,分别是三棱锥模型和不规则锥体模型。图中水面以下表示被水体淹没的部分。2种锥体的横截面分别如图1(b)和图1(d)所示。图中横截面是对水库坝址断面的抽象描述。在横截面坐标系中,纵坐标D表示水库坝址断面的水深,横坐标W表示库水面与坝址断面交线的宽度。为了便于依据锥体模型推导水库库容特性的表征函数,2种锥体模型的横截面被假设为轴对称。在此前提下,本文采用幂函数刻画不规则锥体横截面的形状,d表示水深,w表示阴影部分的底宽的一半,a和b是参数。由图1(b)和图1(d)可知,三棱锥的横截面是不规则锥体横截面的特例,此时幂函数的参数b=1。显然,三棱锥模型是不规则锥体模型的特例,与不规则锥体模型相比,三棱锥模型对水库形态的描述更加抽象与简化。 首先,根据三棱锥模型推导水库库容特性表征函数的数学表达式。假设水深为d,此时水体的横截面的面积s=dw,水体的高h=dtanθ。据此,由三棱锥的体积公式可以求得水体的体积V为 式中:θ表示三棱锥横截面的对称轴与棱的夹角,如图1(a)所示,此夹角是对水库坝址断面与水库深弘线的夹角的抽象。 将d=Z-Z0代入式(4),推导出三棱锥模型对应的水库库容特性表征函数fslz(V)的数学表达式为 (5) 式中:Z表示水库水位;Z0表示库底的海拔高度。 其次,根据不规则锥体模型推导水库库容特性的表征函数。由图1(c)可以看出,水体部分不是规则锥体,难以用已有求积公式计算水体体积。为此,本文采用积分的方式计算水体体积。假设水深为d,此时水体的相关要素为: h=dtanθ; (6) (7) (8) (9) 式中:dx为x处的水深;wx为x处底宽的一半。 根据以上相关要素,采用积分方法计算图1(c)截面的面积s为 (10) 进一步,将面积s沿着水库上游方向进行积分,求得水体的体积为 将d=Z-Z0代入式(11),推导出不规则锥体模型对应的水库库容特性表征函数fbgz(V)的数学表达式为 Vb/(2b+1)+Z0。 (12) 式(5)和(12)分别是三棱锥模型和不规则锥体模型对应的水库库容特性的表征函数。可以看出,无论是根据更抽象简化的三棱锥模型,还是根据更符合实际且复杂的不规则锥体模型,导出的水库库容特性表征函数的通式fmi(V)(一般形式)是一致的,即 Z=fmi(V)=α1Vα2+α3。 (13) 式中:α1、α2和α3是参数,从物理意义上来看,这3个参数分别反映了水库断面形态、水库库底坡降以及水库库底高程,如式(5)和式(12)所示。 由式(13)可知,参数具有较明确物理意义的水库库容特性表征函数是三参数幂函数。从其推求过程可以看出,参数α1、α2和α3可以根据水库的形态参数a、b和θ直接推求。该方法一定程度上能够给出参数α1、α2和α3的合理取值,但该方法并不是最佳的,因为锥体模型始终只是水库形态的一种抽象表征,两者之间极可能存在系统性偏差。因此,为减小系统性偏差带来的影响,可采用优化方法率定参数α1、α2和α3,即通过对参数进行优化使函数尽可能逼近水库的实测库容-水位离散数据点。 除水库库容特性外,水库面积特性是水库的另一基本特性。根据水库库容特性的三参数幂函数模型,采用微分方法可以非常简便地获得水库面积特性的表征函数,即根据式(14)推求得到式(15)。由于本文的研究重点是水库的库容特性,因此以下仅给出水库面积特性的表征函数供读者参考,而不对其进行深入阐述。 (14) (15) 根据式(13),推求水库库容特性的表征函数三参数幂函数的一阶导数和二阶导数,分别为: (16) (17) 由式(1)可知,为准确反映水库库容特性的基本数学性质,表征函数应满足一阶导数为正、二阶导数为负的基本要求,如式(18)所示,即 (18) 由式(18)可推出 (19) 最后得到 (20) 由式(18)—式(20)可知,在优化水库库容特性的三参数幂函数的参数时,应保证其参数在α1>0和0<α2<1的取值范围内。 在第2节,通过严密推导,获得了水库库容特性的一种通用性表征函数,即三参数幂函数,该函数在表征水库库容特性时,其参数具有明确的物理意义。为了更加全面认识三参数幂函数在表征水库库容特性上的优劣,需对三参数幂函数的拟合优度性能进行分析,并通过与其他几种表征函数进行比较来验证其准确性和优越性。下面给出了另外3种表征函数: Z=fduo(V)=β1V3+β2V2+β3V+β4; (21) Z=fzhi(V)=γ1exp(γ2V)+γ3exp(γ4V) ; (22) Z=fdui(V)=λ1ln(Vλ2+λ3)+λ4。 (23) 式中:Z为水库水位;V为对应的水库库容;fduo(V)、fzhi(V)和fdui(V)分别为表征水库库容特性的多项式函数、指数函数和对数函数;βi、γi和λi为待优化的模型参数(i=1,2,3,4)。 根据实测库容-水位离散数据点,利用MatLab 2021b的曲线拟合工具箱可以方便地确定本文所述各类表征函数的参数取值。其中,对于指数函数fzhi(V)、对数函数fdui(V)以及幂函数fmi(V),采用工具箱中的信赖域反射算法[17]率定参数,而对于多形式函数fduo(V),直接采用工具箱求解线性最小二乘问题的正规方程即可获得参数的率定结果。 本研究采用平均绝对误差(Mean Absolute Error,MAE)、平均相对误差(Mean Realative Error,MRE)、均方根误差(Root Mean Square Error,RMSE)和确定系数(R2)4个拟合优度指标评价各类水库库容特性表征函数的准确程度。拟合优度指标的计算公式见文献[1] 。 本文以长江中上游37座水库为实例研究对象,包括金沙江中下游10座水库、雅砻江7座水库、岷江1座水库、大渡河1座水库、嘉陵江4座水库、乌江9座水库、清江3座水库以及长江干流三峡和葛洲坝水库,各水库的地理分布情况如图2所示。 图2 长江中上游37座水库的地理位置示意图Fig.2 Location of 37 reservoirs in the middle and upper reaches of Yangtze River 采用式(13)、式(21)—式(23)4种函数拟合37座水库的实测库容-水位离散数据点。各水库库容特性的三参数幂函数模型的参数率定值如图3所示。由图3可以看出,各水库库容特性的三参数幂函数模型的参数α1和α2的率定值均在式(18)指定的范围内,表明各水库的三参数幂函数均能准确地反映水库库容特性的基本数学性质(见式(2))。而对于多项式函数、指数函数和对数函数这3种水库库容特性表征函数,分析其一阶、二阶导数可知,要用这3种函数准确描述水库库容特性的基本数学性质是较困难的。因此,不再对参数取值的合理性进行分析。一般而言,在不要求函数参数具有明确物理意义的情况下,只要函数能够以较高精度拟合实测库容-水位离散数据点,即可认为该函数是可用、实用的,这也是多项式函数、指数函数等能够被广泛应用于水库库容特性表征的主要原因。 图3 37座水库的库容特性的三参数幂函数模型的参数率定值Fig.3 Calibrated parameter values of three-parameter power function models for the capacity characteristics of 37 reservoirs 在4.2节的基础上,研究以37座水库的实测库容-水位离散数据点为基准,计算了各水库4种库容特性表征函数的拟合优度指标,即平均绝对误差、平均相对误差、均方根误差和确定系数指标,如图4所示。 图4 37座水库的4种库容特性表征函数的拟合优度指标Fig.4 Goodness of fit indexes of four function for the capacity characteristics of 37 reservoirs 首先,从图4(d)可以看出,不同类型水库库容特性表征函数的确定系数R2均在0.94以上,表明4种库容特性表征函数均能较好地拟合37座水库的实测库容-水位离散数据点。其次,根据图4综合比较不同容积特性表征函数的4个指标可以发现,多项式函数和对数函数的拟合优度明显较差,指数函数的拟合优度次之,三参数幂函数模型的拟合优度显著优于前三者。此外,还可以看出,在拟合不同水库的实测库容-水位离散数据点时,多项式函数、指数函数和对数函数的拟合优度指标表现出较大的波动,对于一部分水库,拟合性能很好,而对于另一部分水库,拟合性能很差。该现象一定程度上说明了这3种库容特性表征函数存在适用范围有限的问题。与之相反,对于三参数幂函数,其在描述不同水库的库容特性时均具有相近且更优的拟合性能。显然,与另外3种库容特性表征函数相比,三参数幂函数的适用性更好。 由上述分析可知,从拟合优度的角度看,式(13)给出的三参数幂函数是表征37座水库的库容特性的最佳函数模型, 加之三参数幂函数模型具有参数物理意义明确且能准确反映水库库容特性的优点, 可以进一步推断三参数幂函数在描述水库的库容特性上具有更广泛的适用性和更高的准确性。 图5给出了三参数幂函数对9座水库实测库容-水位离散数据点的拟合曲线, 可以直观地看出, 曲线与实测离散数据点非常贴合, 进一步印证了以上结论。 本文以长江中上游流域37座水库为研究对象,开展了水电站水库库容特性解析与建模研究。首先,对水库的形态特征进行抽象,构建了描述水库一般性形态特征的三棱锥模型和不规则锥体模型;其次,依据锥体模型导出了表征水库库容特性的三参数幂函数模型,并根据水库库容特性的数学性质,给出了三参数幂函数模型的参数取值范围;最后,为验证三参数幂函数的适用性、可靠性和优越性,应用其拟合37座水库的实测库容-水位离散数据点,从拟合优度角度对其性能进行评价。本研究得到了以下结论: (1)在采用三棱锥模型和不规则锥体模型描述水库形态特征的条件下,水库库容特性的表征函数是三参数幂函数。与多项式函数、指数函数、对数函数比较,三参数幂函数的参数具有明确的物理意义,其参数反映了水库断面形态、水库库底坡降以及水库库底高程等水库形态特征。 (2)与其他三种函数模型比较,三参数幂函数的拟合优度性能更优,加之三参数幂函数具有物理意义明确且能准确反映水库库容特性的基本数学性质的优点,三参数幂函数被证明是一种适用性广、可靠性高、物理意义明确的水库库容特性表征函数。 本文仅针对水库的静水库容特性开展了研究,推导了能够准确刻画水库静水库容特性的三参数幂函数,而尚未对水库的动水库容特性进行研究,在完备性上存在不足。一般情况下,使用静水库容特性可以满足要求,但在防洪调度期间,尤其是调度决策需要考虑库区淹没时,必须依据水库的动水库容特性。因此,有必要进一步开展水库动水库容特性解析与建模研究,建立能够准确描述水库动水库容特性的数学模型,为水库动库容精确计算提供模型支撑。2 水库库容特性的数学模型
2.1 水库的几何抽象模型

2.2 水库库容特性的表征函数
2.3 水库库容特性表征函数的参数取值范围
3 水库库容特性表征函数的性能评价
4 结果与讨论
4.1 实例研究对象

4.2 水库库容特性表征函数的参数率定结果

4.3 水库库容特性表征函数的拟合优度分析结果
5 结 论
