基于镜眼联合模型的单光镜片设计及制造

许崇祥，张中祥，燕卫江，苏宇锋，贾志刚

（郑州大学 机械与动力工程学院，河南 郑州 450001）

引言

人的感觉器官对外界信息的获取约80%来自于视觉[1]。健康的视觉是良好生活、学习、交流的保证。近年来，随着电子产品的普及，无论是青少年还是成年人，每天长时间面对各种发光显示设备，引发多种眼部疾病[2]。特别是以近视、散光为代表的屈光不正已成为青少年普遍面对的健康问题。各种屈光不正矫正技术有着广阔的应用市场[3]。目前，常见的屈光不正矫正方法有：框架眼镜、角膜接触镜及激光角膜手术等。其中长时间佩戴角膜接触镜会因摩擦角膜导致眼部感染，从而引发炎症，且镜片本身为消耗品，使用成本较高。激光角膜手术存在手术费用昂贵，对角膜的磨切去除造成不可逆的损害，同时可能引起一些长期的后遗症，如眼睛干涩、高阶像差增加等不被人们轻易接受[4]。相比而言，框架眼镜具有方便、经济、可逆、无副作用等优点，是目前最为普遍应用的矫正方法。

佩戴式框架眼镜有诸多优点的同时，也存在若干不足之处有待改进。1）传统镜片一旦加工完成，其矫正能力就固定不变，而人眼受到光照环境、心理因素的影响，其像差是时刻变化的，这会造成某些时刻镜片矫正能力不足或过量，造成用眼不适。解决办法在于开发具有动态矫正能力的镜片[5]。2）目前的镜片仅能矫正低阶像差，随着像差测量技术的发展，对人眼全像差的补偿可达到超视力的效果成为未来发展趋势[6]。3）对于普遍应用的单光镜片，佩戴状态不同视角下，人眼实际感受到的矫正能力并不均一[7]，其原因在于镜片设计时没有考虑到眼球旋转带来的视角变化问题。造成的结果是，虽然镜片的不同区域在焦度计下测得的屈光度数恒定不变，但在佩戴时，人眼实际感受到的屈光力是变化的。这种屈光能力的变化在某些情况下，比如暗光环境下，在视角较大时存在明显的像差矫正不足，从而带来视觉模糊。随着人们对视力精准化的追求和镜片设计理念的发展，越来越多的镜片优化设计方案被提出。李念宁采用多目标优化遗传算法[8]设计了单光非球面眼镜片，利用算法随机生成多组前弯和非球面系数，通过光线追迹计算像差大小，使设计的眼镜片降低了像散和畸变。BARBERO S[9]提出了一种基于径向折射率梯度(radial refractive gradient，RRG)镜片的设计方法来减少镜片周边区域离焦现象，并通过实验验证了方法的可行性。张海平[10]将非球面方程应用到多焦点镜片，利用连续变化的曲率来调节镜片光焦度分布和减小像散。但是，目前的镜片设计方法并没有考虑人眼实际佩戴时的视角变化问题。

针对上述第三个问题，本文通过建立镜眼联合模型，充分考虑在人眼旋转时，应用镜片的不同区域及相对应的不同入射光线角度变化的问题，对传统单光镜片设计方法进行了改进，实现在佩戴时不同视角下，人眼实际感受到的矫正力保持恒定。基于镜眼联合模型，生成镜片面形数据，在数控机床上实现镜片的加工制造[11-13]，并对加工后的镜片面形及屈光度进行了测量，初步验证了模型的有效性。

1 基于镜眼联合模型的单光镜片设计

镜眼联合模型侧视图如图1 所示。图1 中镜片放置在人眼角膜前，O为 眼球旋转中心，O′为镜片后表面中心，物体发出的入射光经镜片折射后，通过角膜，汇聚在视网膜黄斑中心凹处。平视时，光轴与视轴重合，穿过镜片中心、角膜前表面中心及眼球旋转中心[14]。当眼球旋转或视角变化时，入射光线与镜片表面夹角随之变化，从镜片前表面到角膜前表面的光程也随之改变，这样会带来镜片矫正能力的改变。因此，需要改变不同视角下的镜片面形，以保证光程恒定，最终使人眼实际感受到的镜片矫正屈光力恒定。假设镜片前表面为基弧，则需要在镜眼联合模型基础上，考虑视角变化，设计出镜片后表面面形，通过面形的变化，调节因视角改变而引起的光程差异，使人眼实际感受到的镜片屈光力保持恒定。

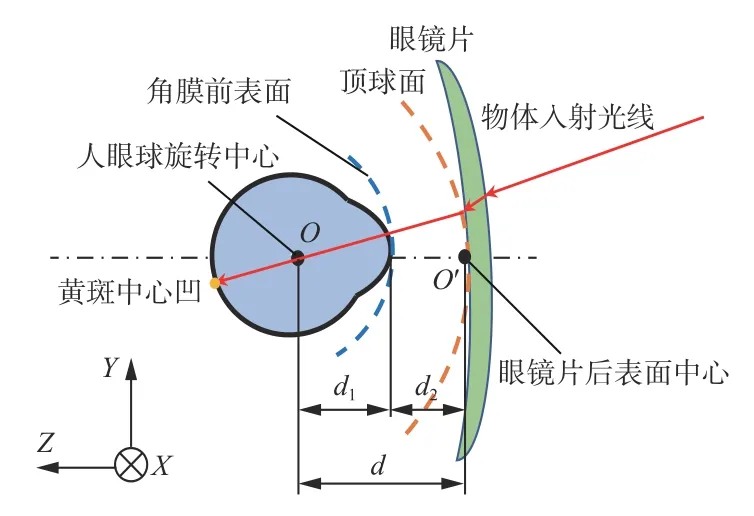
图1 佩戴状态下的镜眼联合模型Fig.1 Lens-eye joint model in wearing state

图1 中，d为镜片后表面中心O′到眼球旋转中心O的距离；d1为眼球旋转中心与角膜前表面中心的距离[15]；d2为角膜前表面中心与镜片后表面中心O′的距离，d=d1+d2。以镜眼联合模型为基础建立坐标系，如图2 所示。以人眼球旋转中心为原点建立世界坐标系O-XYZ，以镜片后表面几何中心Ol为原点建立镜片坐标系Ol-XlYlZ。X轴方向表示水平视角，右为正，Y轴方向表示垂直视角，上为正，Z轴正向指向人眼视网膜。当人眼通过镜片观察物体时，视轴所在的直线必然会与镜片平面相交，交点为 (xl,xl,xl)，即为不同视角下镜片表面使用点的坐标。

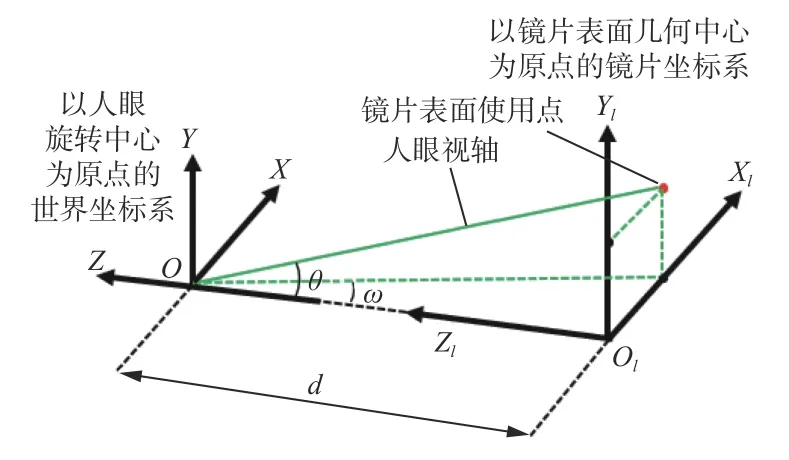
图2 镜眼联合模型坐标系Fig.2 Coordinate system of lens-eye joint model

从图2 推导出镜片坐标系中镜片表面使用点与世界坐标系下视轴的视场角对应关系：

式中：θ为人眼垂直视角；ω为人眼水平视角。根据人眼视轴视角 (θ,ω)可求出人眼视轴所在直线的方向向量为

假设某视轴所在直线过点M(mx,my,mz)时，则视轴所在直线参数方程为

式中t为人眼视轴所在直线方程的参数变量。

显然人眼视轴所在直线经过人眼转动中心O，即为M(0,0,0)时，人眼视轴所在直线参数方程为

对于镜片表面所在的平面(假设视轴与镜片后表面交点为中心的微小区域为平面)，由该平面上任意3 个不重合的点，可求出2 个不平行的向量N1、N2，通过向量的叉乘求出该平面的法向量P(Px,Py,Pz)。假设眼镜片平面过点N(nx,ny,nz)，则镜片平面的点法式方程为

在世界坐标系O-XYZ下，以视场角为旋转角度 (θ,ω)的人眼视轴的直线参数方程(3)与镜片表面的平面方程(4)的交点 (u=x,v=y,w=z)，就是人眼不同视角观察物体时通过镜片表面时的使用点，通过设计每个使用点的屈光度，就可以得到整个眼镜片后表面的屈光度分布图，从而计算出整个眼镜片的面形数据。

不同视角下镜片平面使用点的坐标一定满足视轴所在直线参数方程和镜片平面点法式方程，联立式(3)和式(4)得出：

根据人眼实际观察状态可知，上式分母必不为零，即视轴所在直线与镜片平面方程必有交点，求出参数变量t后，带入视轴直线参数方程(3)，即可求出不同视角下镜片平面使用点的坐标 (xl,yl,zl)。

根据空间坐标变换原理[16]，图2 中世界坐标系O-XYZ与镜片坐标系Ol-XlYlZl的变换关系为

式中：旋转矩阵R为

平移矩阵Q为

通过空间坐标变换原理，求出在世界坐标系O-XYZ下，不同视角镜片平面使用点的坐标(x,y,z)。然后求交点距人眼旋转中心O的距离p:

再求出镜片平面使用点与人眼角膜前表面的距离p1：

最后，根据所提出的设计原理计算眼镜片的面形数据。为了在任意视角时，人眼角膜前表面上实际获得的镜片屈光度FJM恒定不变，根据计算等效屈光度计算公式[17]可推导出，镜片平面上使用点的屈光度FJ为

式中：FJM为人眼在角膜前表面上获得的屈光度补偿值。

假设以镜片前表面作为基弧，通过改变镜片后表面屈光度来改变镜片整体的屈光度，则根据单光眼镜片设计原理，可求出镜片后表面的屈光度FH为

式中FQ为眼镜片前表面的屈光度。

通过眼镜片曲率半径计算公式，可求出后表面的曲率半径rH为

式中n为镜片材料的折射率。

利用式(11)即可获得基于镜眼联合模型所设计的眼镜片的表面面形。

2 镜片设计

基于上述镜眼联合模型的镜片设计方法，编写相应的Matlab 计算程序，以角膜表面实际感受到的屈光度FJM=-6.00 D 为例，计算出镜片的理论屈光度FJ的分布图，如图3 所示。图3 中，d取平均值27 mm，d1取平均值14 mm，所设计的镜片直径为70 mm，对应最大视角 ±52°。图3 给出了视角从0°～25°时对应镜片表面屈光度分布图，该视角范围满足实际佩戴的需求。当视角更大时，人会转动头部，使视角在舒适范围内，同时镜片的边缘区域也会被切割，以适配眼镜框架。

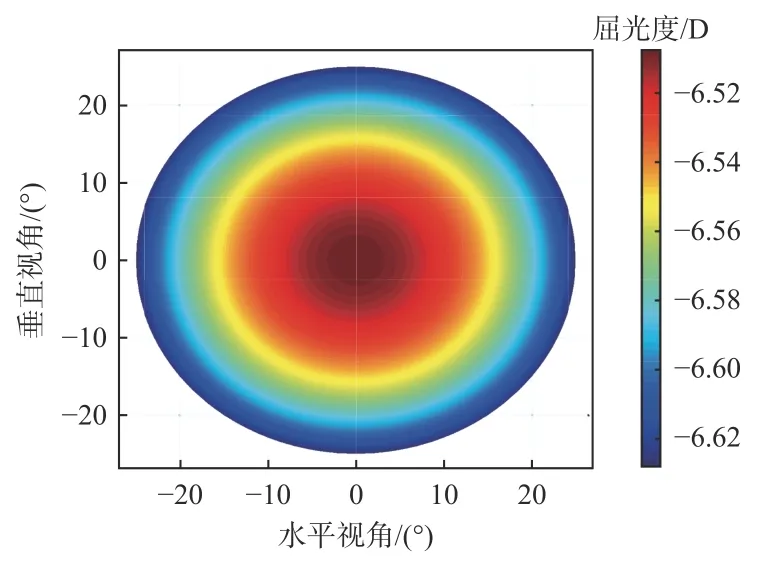
图3 镜片表面屈光度分布图Fig.3 Diopter distribution diagram of lens surface

从图3 可以看出，为了实现人眼在不同视角观察时镜片都可以提供恒定的屈光度补偿，在设计镜片时要保证镜片表面上的屈光度分布呈连续渐进变化。这是因为在模拟实际佩戴状态下，测量单光球面镜片表面屈光度时，测量的顶球面与人眼旋转中心的距离会随着视场角的变化而逐渐变化，所以实际佩戴单光眼镜片时，人眼在不同视角下使用单光镜片的不同区域观察时，单光镜片提供的屈光度补偿是变化的。通过本文提出的镜眼联合模型的设计方法，计算出来的镜片表面屈光度数据，从中心点向四周边缘区域呈现连续变化并且逐渐增加的趋势。这样可以补偿传统单光球面眼镜片在佩戴状态下，人眼角膜处实际感受到的屈光度从中心点向边缘区域连续逐渐减少的不足。理论计算出的镜片表面屈光度分布呈同心圆且数值从中心向边缘区域逐渐变大。这种渐变速度随着设计镜片中心处屈光度的不同而变化，设计镜片中心处屈光度越大，渐变速度越快。

假设镜片前表面为基弧，取FQ=+2.50 D，由公式(10)及公式(11)可得镜片表面的面形变化，呈现中心对称形式，如图4 所示。

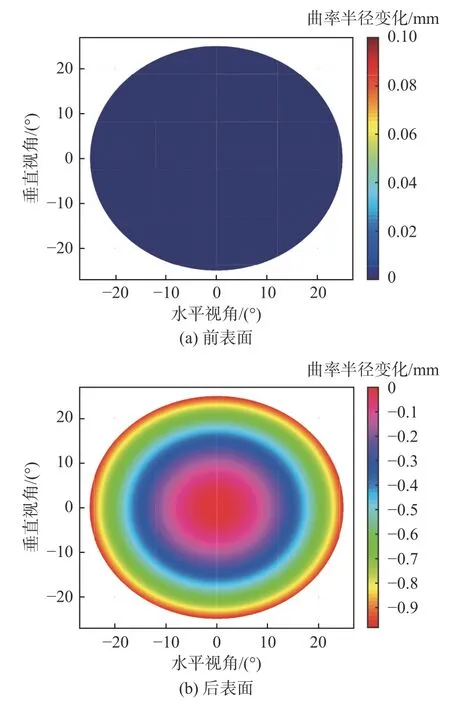
图4 镜片表面曲率半径变化图Fig.4 Diagram of curvature radius variation of lens surface

3 镜片的加工及测量

将图4 中数据导入数控机床，机床能够实现横向及纵向0.1 μm 的位移精度，1″的旋转精度，可满足本文设计镜片微米级加工精度的要求。选择前表面FQ=+2.50 D 为基弧的镜片毛坯进行镜片加工，并对其后表面对应视角 ±25°内的区域进行切削和抛光处理，得到加工后的镜片如图5 所示。设计加工镜片的标称尺寸dn=70 mm，实际加工出的未切割镜片直径有效尺寸为69.9 mm，镜片直径使用尺寸为69.8 mm，允差值为0.1 mm，符合镜片尺寸的允差[1]。

图5 加工镜片实物图Fig.5 Physical drawing of manufactured lens

由于镜片的设计及加工的旋转对称性，对加工后的镜片后表面的水平及垂直中心线进行了测量，相应的面形变化及与理论计算值的差值如图6所示。从图6 可以看出，受加工精度的影响，在加工的镜片边缘区域出现了较大的误差，中心区域的加工误差较小，曲率半径变化值最大为1.1 mm，能满足加工面形变化要求。

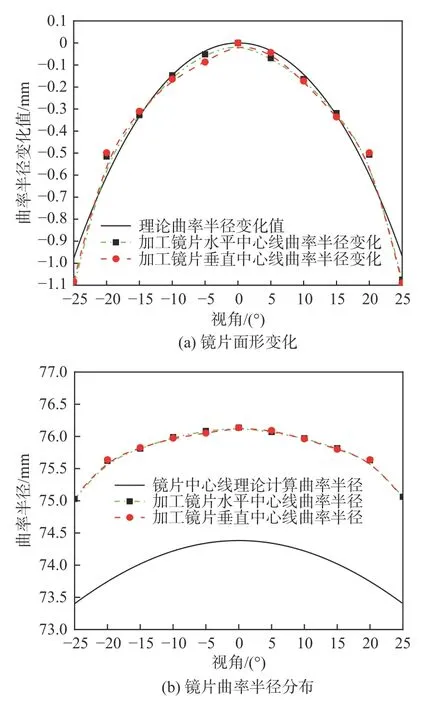
图6 镜片面形数据图Fig.6 Surface data diagram of manufactured lens

使用焦度计对镜片水平中心线及垂直中心线上的屈光度进行测量[18]，测量结果如图7 所示。从图7 可以看出，镜片屈光度呈中心向边缘渐近变大趋势，与理论设计相符。受加工精度的影响，在镜片边缘区域呈现较大的误差，但整体屈光度及其变化趋势与理论计算相符，满足设计要求。镜片后表面屈光度为-6.30 D，屈光度误差值最大为0.23 D，镜片加工误差满足镜片设计误差0.25 D。后续工作将采用更高精度的加工设备对镜片进行加工，使镜片表面屈光度误差小于0.12 D。同时希望出现一种适合该种镜片的加工方法，以期改善误差值。

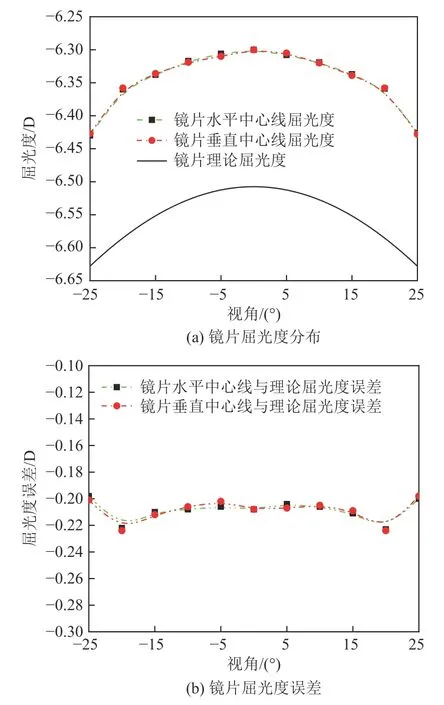
图7 镜片屈光度分布与误差Fig.7 Diopter distribution and error of manufactured lens

4 结论

本文提出了一种基于镜眼联合模型的单光镜片的设计方法。根据所建模型，假定人眼视角变化使用镜片不同区域时，到达人眼角膜前表面的有效屈光度保持恒定，从而对现有的镜片设计进行优化，重新求解出镜片不同区域屈光度的分布，最终获得镜片的面形变化数据。将面形数据导入数控机床，对镜片毛坯进行加工，制作出人眼实际可感受到屈光度恒定的单光镜片。使用自动焦度计对加工后的镜片屈光度进行测量，测量结果表明，屈光度分布呈现从镜片中心向镜片四周渐变趋势，与理论计算一致，初步验证了所建模型及设计方法的有效性。在佩戴时，能够使人眼实际感受到该镜片不同区域的矫正效果保持恒定。受加工方法及加工精度的影响，所加工的镜片存在一定的面形误差，进而引起了屈光度与理论设计值的偏差。下一步将对加工方法进行优化，选用更高精度的加工机床，同时将开发一套主客观评价方法，对实际佩戴时镜片提供给人眼角膜的屈光度补偿值进行定量化评价。同时基于本文提出的镜眼联合模型，测量镜片视场角10°以内的圆形和10°～25°的点扩散函数PSF，利用计算成像方法[19]对镜片成像质量进行检测,并根据测量结果进一步改进镜片的成像质量。

我国是眼镜制造大国，而非制造强国，国外厂商掌握着高附加值的镜片设计及制造市场。本文所提出的基于镜眼联合模型的镜片设计及制造方法，有助于提高我国高端镜片的生产水平及市场占有率。