融合交互强度的优化社交推荐算法
2024-02-18周璐鑫李曼蒋明阳张雷
周璐鑫 李曼 蒋明阳 张雷
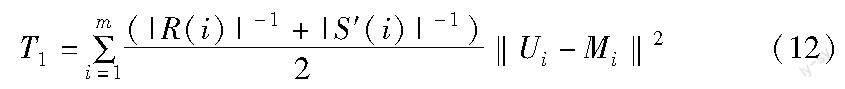
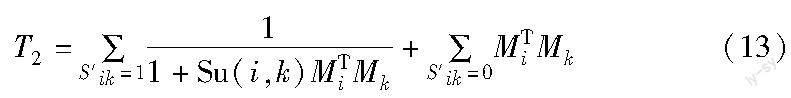
摘 要:针对现有社交化推荐算法忽视了评级数据与社交信息之间关联的探索,提出了一种融合交互强度的优化社交推荐算法。首先,利用社交信息和评级数据结合两种相似度丰富社交矩阵;接着,定义用户间交互强度代表用户间复杂关系;最后,利用交互强度与社交关系之间的关联以及用户潜在特征与用户群体参与特征的关联构建新的目标函数,学习用户和项目的潜在特征,实现个性化推荐。在三个真实数据集上进行实验,与基线模型相比,提出算法在推荐预测精度上有显著提升,且在对不同评级数量的用户进行潜在特征学习时,表现出良好的鲁棒性。综上,融合交互强度可以进一步提升社交化推荐算法性能,增强用户体验感。
关键词:社交化推荐; 交互强度; 群体参与矩阵; 矩阵分解
中图分类号:TP301.6 文献标志码:A 文章编号:1001-3695(2024)01-010-0065-07
doi:10.19734/j.issn.1001-3695.2023.05.0280
Improving social recommendation algorithm via incorporating interaction strength
Abstract:Existing social recommendation algorithms ignore the investigation on the association between rating information and social information. To address this issue, this paper proposed a social recommendation algorithm which incorporated interaction strength. Firstly, it utilized social information and rating data to enrich the social matrix by combining two kinds of similarities. Secondly, it defined the interaction strength to represent complex relationship between users. Finally, it introduced a new objective function to learn features of users and items for personalized recommendation using two types of associations, namely the association between interaction strength and social relationships, and the association between features of users and participation features of group which users belonged to. Experimental results on three real-world datasets indicate that the proposed algorithm shows significant improvement in terms of recommendation prediction accuracy compared with existing baseline mo-dels. Furthermore, the proposed algorithm behaves good robustness in learning latent features for users with different number of ratings. Based on the above observations, it can infer that incorporating interaction strength is beneficial to enhancing social recommendation performance and improving users experience.
Key words:social recommendation; interaction strength; group participation matrix; matrix factorization
0 引言
隨着社交网络的快速发展,人们面临着信息的爆炸式增长。如今用户在进行挑选和决策时极大地受益于有效的信息获取方式,推荐算法凭借其出色的信息过滤和数据挖掘能力在短时间内有效地为用户提供个性化推荐。
简单推荐算法假设用户独立决策且不受他人决策的影响,然而在现实生活中,客户在购买商品或服务时往往倾向于相信熟人。因此,与传统推荐算法相比,融合社交信息的推荐算法能够有效改善用户冷启动问题[1,2],并显著提高推荐的准确性和可解释性。在社交化推荐算法中,认为用户仅考虑直接社交朋友影响的推荐为基于直接社交的推荐算法,然而除了直接社交外,社交信息还包括其他复杂的关系,例如,两社交信息接近的用户可能处于相同的群体内,在电影品味上可能相似[3,4]。现有研究结果表明,考虑间接社交关系的推荐[5~9]效果往往优于仅考虑直接社交关系的推荐效果。
近些年来,基于矩阵分解(matrix factorization,MF)的推荐方法[10]应用广泛,通过对用户项目评级矩阵进行分解得到潜在的用户和项目特征,再将两个特征矩阵相乘对不完全评级矩阵进行补全。大多数基于矩阵分解利用社交信息的推荐算法将推荐过程分为挖掘间接的社交关系以及基于矩阵分解学习用户和项目的潜在特征两个阶段。尽管两阶段法极大地改善了推荐效果,但仍然存在一些问题。在挖掘间接社交关系时,现有算法通常仅考虑单一的用户评级信息或社交信息,忽略了两者对用户间间接关系挖掘的不同贡献。此外,大多数基于矩阵分解的推荐算法在用户和项目潜在特征的学习上未能挖掘复杂的社交关系与用户潜在特征之间的关联。针对上述分析,本文在矩阵分解的基础上提出一种融合交互强度的优化社交推荐算法。主要工作如下:a)为综合考虑用户评级信息和社交信息对用户间间接关系的影响,计算用户间好友相似度和评级相似度,通过线性组合得到用户的潜在好友,补充社交矩阵;b)为挖掘复杂社交关系与用户潜在特征间的关联,本文定义用户间交互强度来代表复杂社交关系,融合交互强度与用户潜在特征之间的关联提出一种新的目标函数以学习用户和项目的潜在特征。在三个真实数据集上进行实验,结果表明,本文算法可以有效提高推荐预测精度。
1 相关文献
现阶段利用社交信息改善推荐性能的方法有基于图的推荐[11~13]、基于深度学习[14,15]的推荐和基于矩阵分解[6~8]的推荐。其中,矩阵分解由于具有简单、推荐精度高和易扩展等优点,成为研究者构建推荐系统的首选模型之一。社交化推荐算法按照社交信息的使用情况可分为基于直接社交关系的推荐算法和基于间接社交信息的推荐算法。
1.1 基于直接社交关系的推荐算法
基于直接社交关系的推荐算法仅考虑直接相连的用户社交关系,认为有社交关系的用户具有相似的偏好,利用其优化推荐算法。社交化推荐算法有两种实现形式:a)同时将评级矩阵和社会关系矩阵进行分解以学习用户和项目潜在特征。最经典的是Ma等人[16]提出的将社交信息与评级信息共同分解的SoRec模型;随后,有研究基于SoRec提出了改进模型,如TrustMF[17]和TrustSVD[18]。b)利用社交关系来调整用户的潜在特征,代表模型有Jamali等人[19]提出的SocialMF,它在STE [20]的基础上将信任传播机制引入矩阵分解模型;此外,Ma等人[21]将用户的信任关系作为正则化约束条件,提出了基于社交信息正则化的矩阵分解框架SR2。然而在大多数推荐系统中,明确的社交信息并不总是可靠的,这限制了社交化推荐算法的发展。
1.2 基于间接社交关系的推荐算法
尽管直接社交关系在一定程度上改善了推荐系统,但面对缺少社交关系的用户,其缺乏解决用户冷启动问题的能力;同时除了社交好友间的影响外,社交信息还包括其他的复杂关系。为了更充分地利用社交关系,有研究尝试考虑相似用户、用户群体等概念来提取间接社交关系,提高推荐性能。
Ma[6]提出了内隐社交推荐的实验研究,利用隐式社交信息改进推荐算法,这项研究对社交化推荐技术提供了额外见解,也扩大和传播了社交化推荐算法的效用。Zhao等人[22]提出的SBPR模型根据社会关系将项目分为三类,并定义它们之间的评级关系来学习特征。Yu等人[23]按照相似度对所有用户的潜在朋友进行探索,根据异构图上给定的相似度关系将项目分为五类学习评级函数。Reafee等人[7]提出的EISR模型通过社交关系链接预测得到内隐社会关系,同时考虑显性和隐性社交关系建立了概率矩阵分解模型,然而在这一方法中,链接预测的阈值选取是一个难题。不同于EISR模型,Li等人[8]提出的ReTrustMF利用社会学六度理论拓宽社交关系链,寻找隐性社交朋友,避免了阈值设置不合理带来的问题。此外,还有一些方法从其他角度利用社交信息进行推荐。Tang等人[24]从社交网络中提取异质社会关系和弱依赖关系对评级矩阵分解过程中的潜在用户特征进行调整。Chen等人[25]将社交知识影响和社交消费影响整合到了矩阵分解模型中。Ahmadian等人[26]提出的RTARS算法基于用户间信任关系和评级信息建立了用户声誉模型来寻找用户近邻。Liu等人[27]提出的InSRMF算法使用社区成员资格来间接表示用户间的社交关系,并将评级矩阵和社交矩阵同时进行矩阵分解,学习用户和项目的潜在特征。Al-Sabaawi等人[28]采用多步资源分配的方式识别社交中的隐藏关系,丰富用户社交信息达到提升推荐的效果。Duan等人[29]提出ETBRec模型,通过用户活跃程度与被信任程度选择专家用户,挖掘社交好友和专家用户对用户的影响构建新的目标函数,学习用户和项目的潜在特征。Weng等人[30]提出的SRGRA模型,基于灰色关联分析计算用户间的相似度,建立包括内隐社交关系的矩阵分解模型。Ahmadian等人[9]提出的SORIR算法将隐式关系整合到推荐算法中,为显式关系不足的用戶提供更加准确的推荐。
需要指出的是,当前的社交化推荐算法在不同程度上提高了推荐效果,但仍存在一些问题,如挖掘用户间接关系时使用的信息单一、忽略用户间社交关系的复杂性、未能挖掘用户间复杂关系与用户间潜在特征的关联等。本文算法通过对用户好友相似度和评级相似度进行线性组合,可以避免信息使用单一的问题;进一步,定义交互强度代表复杂的社交关系,同时构建一种基于矩阵分解融合交互强度的目标函数,可以挖掘复杂的社交关系与用户潜在特征之间的关联,学习用户和项目的潜在特征,实现个性化推荐。
2 融合交互强度的优化社交推荐算法
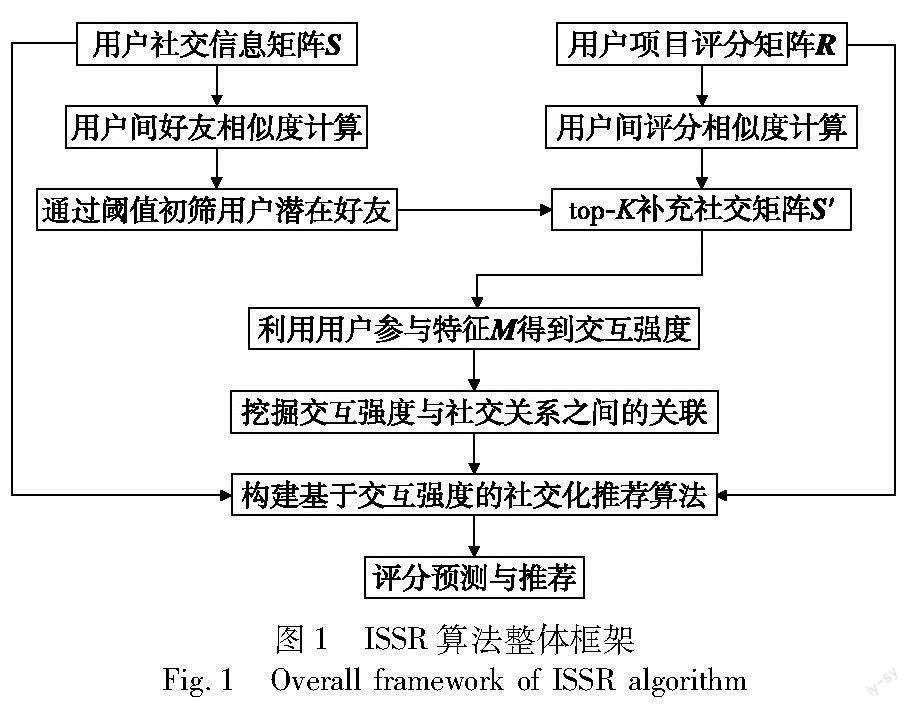
给定用户-项目的评级矩阵和用户间的社交矩阵,实现用户对未知项目的评级预测。为充分挖掘给定的评级信息和社交信息,构建恰当的目标函数学习用户和项目的潜在特征,实现用户对项目评级的预测,本文提出一种融合交互强度的社交化推荐(social recommendation combined with interaction strength,ISSR)算法,算法具体框架如图1所示。具体而言,ISSR算法首先利用社交矩阵S和用户-项目评级矩阵R分别计算用户间好友相似度和用户间评级相似度,通过好友相似度对用户的潜在好友进行初筛,通过评级相似度进行潜在好友再筛,利用top-K原则对社交矩阵进行补充;其次对补充后的社交矩阵S′进行矩阵分解,利用得到的用户群体参与特征M求得用户间的交互强度,用以代表用户间复杂的社交关系;最后挖掘交互强度与社交关系之间的联系,通过共享社交矩阵和评级矩阵中的用户潜在信息构建新的融合交互强度的社交化推荐算法,学习用户和项目潜在特征,提升推荐预测精度。
2.1 社交矩阵补充
2.1.1 用户的好友相似度
合理利用用户社交关系可以帮助获取更好的推荐,但是仅靠同样稀疏的社交网络关系难以挖掘用户受到其他用户的真实影响[6]。由于与用户好友重合度高的人极有可能是用户现实生活中相互熟悉但在社交网络中却没有联系的人,用户的兴趣品味极有可能受到其影响,根据好友相似度高的用户间存在潜在关联原则,寻找初步的用户间潜在社交关系。
为挖掘用户间的初步潜在社交关联,本文通过计算用户间的好友相似度得到在现实中极有可能发生交互的潜在好友。如图2所示,用户集{3,6}是用户i和k的共同好友集,两者有可能通过共同好友的链接成为朋友。
然而由于用户不尽相同的好友数量,两用户相互的好友相似度并不一定相等。若用户i的好友数量为10,用户k的好友数量为50,那么向用户i推荐用户k为好友的推荐程度会高于向用户k推荐用户i。本文考虑用户的好友数量,将用户k对用户i的好友相似度定义为w(i,k),计算方式如式(1)所示。
其中:out(i)为用户i的好友集,选取用户i好友相似度大于阈值ε的用户作为其初步潜在好友。其中ε的数值由实验得到。
2.1.2 用户的评级相似度
虽然好友相似度高的两个用户有可能在现实中交流从而相互影响,但是这个事件对于不愿结识新朋友的用户并非一定发生,即好友相似度高的用户间有机会但并非一定会相互影响。为此,本文通过用户间的评级相似度来佐证采用好友相似度得到的初步潜在社交关联是否成立。当两个用户的好友相似度高,同时评级相似度也高,那么认为两者在现实生活中认识并且彼此之间能够互相影响。
常用的相似度有杰卡德相似度、余弦相似度、皮尔森相似度[31]。其中,杰卡德相似度只使用了评级数量信息,忽略了对评级数值的使用;余弦和皮尔森相似度仅考虑了公共评级,没有充分使用评级数据。因此,本文采用一种通过评级概率分布利用全局评级的海灵格距离(Hellinger distance,HD)来得到用户之间的相似度。在统计学中,海灵格距离被用来衡量两个概率分布之间的相似度,它可以充分利用用户的所有评级信息。式(2)~(4)是根据海灵格距离得到的海灵格相似度shd(i,k)[32]的计算公式。
其中:|ir|是用户i评级r的项目数;|i|是用户i的评级数。
用户间共同评级的电影越多,用户间的相似度也会越高;然而仅考虑共同电影是不够的,若用户i看过5部电影,用户k看过50部电影,那么尽管两者共同电影数相同,但是对彼此的影响是不同的。因此,引入式(5)计算差异因子diff(i,k)。
其中:R(i)是用户i评级的项目集。
本文将海灵格相似度和差异因子进行线性组合,得到用户i和k间的评级相似度Su(i,k)计算公式为
Su(i,k)=θshd(i,k)+(1-θ)diff(i,k)(6)
其中:权重θ∈(0,1),数值在实验中确定。每个用户按top-K原则,通过好友相似度初筛评级相似度佐证的方式,选取评级相似度高的前K个用户补充社交矩阵S,得到用户社交矩阵S′,缓解社交矩阵的稀疏性。
2.2 融合交互强度的推荐算法模型
本文的社交推荐算法试图通过对评级矩陣和社交矩阵联合分解的方式来捕获用户间复杂的社交关系和用户对项目的偏好。其中用户集是用户项目评级矩阵与用户社交矩阵的公共对象集,因此本文在进行矩阵分解时参考SoRec的分解方式[16]来学习用户和项目的潜在特征。
2.2.1 交互强度的定义
补充后的用户社交矩阵S′较原社交关系矩阵更加丰富可靠。在这种情况下,社交矩阵是一个静态的“0-1”矩阵,即任何一对用户之间的社会关系只有S′ik=1或0两种情况,而用户间复杂的社交关系是难以通过有无代表的,因此本文定义用户间交互强度来间接表示用户间复杂的社交关系。
研究表明对用户所处的群体信息进行挖掘可获取更好的推荐[4,33]。处在同一社会群体中的两个用户往往更容易产生交互,两者更有可能存在相似的偏好。因此,本文通过用户间的交互强度来间接获得用户间复杂的社交关系,让算法体现用户行为对社交关系的影响。一对用户共同存在的群体数越多,两者间产生社交互动的可能性就越强。假设G={G1,G2,…,Gh}表示具有h个群体的群体集,在第f个群体里的第i个用户由Mfi来表示,则每个用户都可以用一个群体参与向量Mi=[M1i,M2i,…,Mhi]来表示。
在现实世界中,由于用户爱好和参与社团积极度不同,用户参与群体的情况各不相同。用数值“0”和“1”来表达用户i在群体f中的参与情况显然是不合适的。一个用户可能同时处在多个群体中,受用户偏好和精力的影响,会导致用户在群体中的参与度降低,其他成员与该用户的交互强度将会减弱,两者间的相互影响也会降低。由此可见,当两个用户同处一个群体中时,决定两者关联的一个主要因素就是两者之间的交互强度,因此定义Mfik=MfiMfk表示用户i和k在群体f中的交互强度。
为了得到交互强度值,本文引入一个非负整数变量Xfik来表示用户i和k同时参加群体f的活动次数[25],则用户i和k在h个群体中的共同活动次数向量为Xik=[X1ik,X2ik,…,Xhik]。假设用户对于出席的群体活动都积极参与,那么用户间的交流就不可避免,因此共同参与活动次数可以表征用户间交互强度值。本文采用参数为Mfik的泊松分布来生成用户i和k在群体f中的整数交互强度值Xfik,定义为
Xfik~Pois(Mfik)=Pois(MfiMfk)(7)
由此可得用户间整数交互强度Xik与社会关系S′ik之间的关系:当S′ik=1时,用户间的交互强度值Xik较大,参数MTiMk较大;当S′ik=0时,用户间的交互强度值Xik较小,参数MTiMk较小。考虑式(6)得到的用户间评级相似度,利用参数Mfi代表用户间交互强度Xfik,构造交互强度与社交关系的关系为
考虑到在S′ik=1时,可能会发生MTiMk过大,导致推荐算法更注重用户社交信息,而忽略了用户项目评级信息,使得学习用户和项目特征时产生偏差。为此,式(8)的S′ik=1部分进行归一化处理,得到式(9)。
2.2.2 融合交互强度的模型建立
矩阵分解模型[10]假设用户对项目的评级只取决于用户和项目之间的交互UTiVj,然而受用户或项目个体的影响,不同用户、不同项目评级之间存在很大的差异。因此,在ISSR模型中考虑平均评级和用户/项目偏差,采用文献[34]中的评级预测计算方式为
考虑到用户潜在特征是受社交关系的影响从评级数据中提取得到,本文假设用户i潜在特征Ui接近他的群体参与特征Mi;进一步,为了建立用户偏好与用户间交互强度的关系,设置用户潜在特征数等于用户群体数。此外,参考TrustSVD[18]提及评价较少的项目在很大程度上会产生过拟合,为了缓解这一问题,本文通过评级数的倒数来增大对评级数目较少用户的惩罚。同理,社交关系较少的用户也将受到惩罚,建立用户潜在特征和用户群体参与特征近似关系为
其中:|R(i)|和|S′(i)|分别是用户i评级的数量和用户i社交关系的链数。
为了将交互强度与社交关系的关联融入ISSR算法,将式(9)的S′ik=1部分控制在(0,1),得到式(13)。
融合交互强度的社交化推荐算法旨在学习用户和项目特征,借助稀疏社交信息补全不完全评级矩阵。本文算法使用补充后的社交关系矩阵,利用交互强度与社会关系之间的关联和用户潜在特征与用户群体参与特征的关联建立新目标函数为
其中:Iij是用户i对j的示性值,当用户i对项目j评级,Iij=1,否则为0;|R(j)|是项目j受到评级的数量;α、β、λ1、λ2、λ3分别为正则化系数,具体数值由实验得到。
本文采用梯度下降法对损失函数进行求解。变量Ui、Vj、Mi、bui、bvj的一阶求导公式如式(15)~(22)所示。
2.3 算法伪代码
ISSR算法使用梯度下降法求解的伪代码如下:
输入:评级矩阵R;社交矩阵S;好友相似度阈值ε;社交关系数量K;评级相似度系数θ;潜在特征维数k;正则化系数α、β、λ1、λ2、λ3;学习率γ和最大迭代次数t_max。
输出:用户潜在特征矩阵U;项目潜在特征矩阵V;用户群体参与特征矩阵M;用户和项目的偏置bu和bv;预测评级矩阵R^。
初始化:初始化用户潜在特征矩阵U,项目潜在特征矩阵V和用户群体参与矩阵M。
利用式(1)计算用户间好友相似度w(i,k),取好友相似度w(i,k)大于ε的用户作为筛选条件得到初步潜在好友。
利用式(6)计算潜在好友间的用户评级相似度Su,取前K个相似用户补充社交矩阵S,得到补充后社交矩阵S′。
while 停止条件不满足(函数值L下降相对小或step for each (i,j)∈Rij 根据式(15)~(22)更新目标函数式(14)的變量: Mi=Mi+γL/Mi; Ui=Ui+γL/Ui; Vj=Vj+γL/Vj; bui=bui+γL/bui; bvj=bvj+γL/bvj; end for step=step+1 end while 利用式(10)预测评级矩阵中的未知评级。 返回U,V,M,bu,bv,R^。 算法的主要计算时间为评估目标函数值L和更新Ui、Vj、Mi、bui、bvj。由于矩阵R和S的稀疏性,目标函数L的计算复杂度为O(|R|+|m|+|S|+|n|),其中|R|和|S|分别为矩阵R和S中的非零项个数。Ui、Vj、Mi、bui和bvj的状态更新计算复杂度分别为O(|R|)、O(|R|)、O(|S|)、O(|R|)和O(|R|)。一共迭代c次后满足停止条件,算法整体计算复杂度为O(c(|R|+|S|+|m|+|n|))。由于算法的计算时间与评级和社交关系的数量之间是线性的,所以可以应用于大规模数据集。 3 实验结果与分析 3.1 数据集 为验证融合交互强度的社交化推荐算法的有效性,本文选取Ciao、LastFM和Epinions数据集进行实验。这三个数据集包含用户间社交关系和用户项目评级信息,详细信息如表1所示。 对于每个数据集,本文将采用五折交叉验证的方法进行训练和测试,并将平均测试性能记录为最终实验结果。 3.2 评价指标 为了验证算法的有效性,本文选用两个具有代表性的精度指标来评价预测效果,即平均绝对误差(MAE)和均方根误差(RMSE),计算方式如下: 其中:Rtest表示测试数据集合。MAE和RMSE值越小,表明推荐算法预测精度越高。 3.3 对比算法 对比实验选取的算法如下: a)SoRec[16]。在共享用户特征向量的前提下,使用概率矩阵分解模型同时分解评级矩阵和信任矩阵。 b)SoReg[21]。认为用户与其信任人具有相似的特征向量,将用户间相似度融入矩阵分解推荐算法。 c)TrustSVD[18]。在SVD++的基础上,增加了用户间显式信任对评级预测的影响。 d)I-TCRec[35]。遵循同一受托人的委托人有相似品味的特点,提出一种新的潜在特征学习算法。 e)RTARS[26]。根据用户间信任关系和评级信息建立了用户声誉模型来求解用户近邻,预测用户评级。 f)InSRMF[27]。认为社区活动对用户有影响,在矩阵分解模型上提出一种基于间接社交关系的推荐算法。 g)ETBRec[29]。通过用户活跃度和被信任度选择专家用户,将好友与专家用户影响融合学习用户特征。 3.4 实验结果与分析 3.4.1 推荐结果比较 通过实验对各数据集参数设置如表2所示。 表3展示了本文ISSR算法与其他对比算法在三个数据集上的实验结果。通过对比实验结果可得到以下结论: a)ISSR算法的推荐效果优于使用直接社交关系的SoRec、SoReg、TrustSVD和I-TCRec,这是由于ISSR挖掘了用户间的间接社交关系,提供了更加可靠的用户间社交关系来提升推荐效果。需要强调的是ISSR虽然未对数据进行降噪处理,但其效果优于对社交信息进行降噪的社交推荐算法I-TCRec。 b)虽然SoRec、InSRMF、ETBRec和ISSR算法在矩阵分解时采用相似的方式,但是ISSR的推荐效果优于其他三个算法。其原因是ISSR中创建的目标函数更有利于用户和项目潜在特征的学习,从而提高了推荐效果。具体而言,ISSR的推荐效果优于使用间接社交关系的InSRMF,其原因是ISSR通过用户项目评级数据和用户社交关系数据补充了社交矩阵,挖掘了更多的潜在社交关系,有助于用户和项目潜在特征的学习。 c)相比于所选取的对比算法,本文ISSR算法在推荐预测精度上显著提升。相较于对比算法中的最优结果,ISSR算法在Ciao、LastFM和Epinions上MAE降低了2.61%、4.27%和3.12%,RMSE降低了2.31%、2.60%和2.22%。一是因为ISSR算法在两阶段都充分利用评级信息和社交信息,二是本文构建的目标函数能够有效提升推荐效果。 3.4.2 不同评级数量实验结果比较 部分评级过少的用户存在冷启动问题。为验证各算法在不同用户评级数量下的鲁棒性,本文将训练集中的用户依据评级数量进行划分,表4展示了数据集Ciao在每组评级数量下的用户占比,可以看到用户评级数少于5、大于100的用户占比较少,评级数量在6~10、11~20、21~40的用户占总用户的20%以上。 依据用户的评级数量对训练集中的用户进行划分后,分析7组用户在数据集上的推荐精度表现,Ciao在不同评级数量的结果如图3所示。发现当用户评级数小于5,各个算法推荐结果显著劣于用户评级数大于5的情况,并且用户评级数大于5的不同分组推荐精度差别不大。因此进一步对用户评级数量进行划分,划分成三组,即0~5组、6~40组和over 40组。 剩余数据集的不同评级结果如表5所示。结合图3,对比本文ISSR算法与对比算法在不同数量评级下的结果可以得到以下结论: a)当用户评级数量极少时,ISSR算法与对比算法的推荐精度都较低,随着评级数量增加,各算法推荐效果均有显著提升。这一现象产生的原因是:评级数据过于稀疏,算法可利用信息过少导致算法缺乏可信度,难以学习合理的潜在特征。 b)ISSR算法的推荐精度在不同的用户评级数量下始终高于其余算法。这是由于ISSR算法在推荐算法的两阶段都致力于挖掘更多的社交信息,从而得到更丰富可靠的社交关系,提升了解决冷启动问题的能力,提高了推荐精度,表明ISSR算法对不同评级数量的用户具有较好的鲁棒性。 3.4.3 复杂性比较 本节评估了ISSR算法的时间复杂度,通过算法运行时间验证ISSR的运行效率。实验运行平台如下:CPU为AMD Ryzen 7 5800H with Radeon Graphics 3.20 GHz,CPU核心数量为8、线程数量为16,内存为16 GB,操作系统为Windows 11。 表6列出不同社交推荐算法在各数据集的运行时间。由表6可知,ISSR算法在三个不同规模的数据集上的运行时间明显优于I-TCRec和ETCRec算法。具体而言,相较于I-TCRec算法,在LastFM、Ciao和Epinions数据集的运行时间分别缩短了约22倍、18倍和230倍;相较于ETCRec算法,在LastFM、Ciao和Epinions数据集的运行时间分别缩短了约3倍、53倍和67倍。 值得一提的是,随着数据集规模的扩大,ISSR与InSRMF算法在运行时间上相差不大。但是根据表3的实验结果,ISSR的推荐精度明显优于InSRMF的推荐精度。这一现象是因为ISSR与InSRMF的计算时间与评级和社交关系的数量之间是线性的,因此运行时间明显少于时间复杂度非线性的I-TCRec和ETCRec,扩大到大规模数据集上,运行时间增长速度也明显更缓慢。 3.5 参数敏感度分析 为了分析本文算法参数对预测精度的敏感度,本文以数据集Ciao为例进行展示,其余数据集参数如表2时推荐效果最优。 a)ε、K和θ。ε、K和θ控制着社交矩阵对ISSR算法的影响。图4表明,随着ε、K和θ的不断增加,推荐算法预测精度均表现为先提升后下降。(a)用户好友相似度的确可以挖掘潜在社交关系,但ε取值过小或过大都会导致其筛选初步好友的功能减弱;(b)合适的用户潜在社交数量可以丰富社交信息,K取值过小或过大会导致改进社交信息效果不佳,甚至干扰用户特征向量的学习;(c)用户的海灵格相似度和差异因子需以一定比例结合才能提升推荐效果,否则会产生用户评级相似度受全局噪声影响或者过于依赖共同评级而导致推荐效果下降。通过实验,参数设置如下:ε=0.1,K=15,θ=0.3。 b)α和β。ISSR算法中α控制着用户潜在特征与用户交互强度之间的近似程度,β控制着用户社交信息对特征学习的贡献。图5表明,随着α和β的不断增加,推荐算法预测精度先提升后下降。(a)用户潛在特征和用户群体参与特征都是用户行为存在近似关系,但当U和M过于近似时,它们将失去各自的特性,从而降低推荐效果;(b)社交信息对预测未知评级是有用的,但当β过大时,推荐算法过度重视社交信息而忽视评级信息,从而导致推荐效果不增反减。通过实验,参数设置如下:α≈10,β≈0.01。 3.6 实例分析 将算法ISSR应用到实际数据集Ciao进行案例分析,以直观地分析模型的有效性。具体而言,ISSR算法的应用主要是通过收集的用户数据(即用户的电影评级数据和用户的社交数据)预测其对电影的评分,并向其提供未观看过的预测评级较高的电影列表作为推荐。首先在Ciao的测试集中随机抽取5个用户,ID分别为[8,14,161,1260,2073],为他们提供电影推荐;然后选用评价指标MAE和RMSE最优情况下的参数,得到上述5个用户对各电影的预测评级,对预测评级进行排序,生成这5个用户的top-20电影列表,得到的结果如表7所示,其中加黑的项目id为用户的实际选择。由表7可知,用户8、14和2073的推荐列表有两部电影击中,用户161的推荐列表有13部电影击中,用户1260的推荐列表有8部电影击中,5个用户的推荐列表平均准确率为0.27。由此可得,本文ISSR算法有较好的预测效果,可以为用户提供个性化推荐,具有应用性。 4 结束语 本文提出了一种融合交互强度的社交化推荐算法(ISSR)。首先,利用好友相似度融合用户评级相似度来补充用户社交矩阵,得到更加丰富可靠的社交关系;其次,定义服从泊松分布的用户间交互强度来代表用户间的复杂关系;然后,通过共享评级矩阵和社交矩阵构建符合交互强度与社交关系关联,用户特征与用户群体参与特征关联的目标函数,学习用户和项目潜在特征;最后,通过实验验证了提出算法的有效性和鲁棒性。在未来的工作中,将进一步考虑项目潜在特征挖掘与数据去噪,进一步提升推荐效果。 参考文献: [1]Zhang Yijia, Shi Zhenkun, Zuo Wanli, et al. Joint personalized Markov chains with social network embedding for cold-start recommendation[J].Neurocomputing,2020,386(4):208-220. [2]Liu Zhiwei, Fan Ziwei, Wang Yu, et al. Augmenting sequential re-commendation with pseudo-prior items via reversely pre-training transformer[C]//Proc of the 44th International ACM SIGIR Conference on Research and Development in Information Retrieval.New York:ACM Press,2021:1608-1612. [3]Tang Lei, Liu Huan. Relational learning via latent social dimensions[C]//Proc of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York:ACM Press,2009:817-826. [4]宗传玉,李箬竹,夏秀峰.基于位置社交网络的用户社区和属性位置簇搜索[J].计算机应用研究,2023,40(9):2657-2662.(Zong Chuanyu, Li Ruozhu, Xia Xiufeng. User community and attribute location cluster search in location-based social networks[J].Application Research of Computers,2023,40(9):2657-2662.) [5]Ma Hao, King I, Lyu M R. Learning to recommend with explicit and implicit social relations[J].ACM Trans on Intelligent Systems and Technology,2011,2(3):article No.29. [6]Ma Hao. An experimental study on implicit social recommendation[C]//Proc of the 36th International ACM SIGIR Conference on Research and Development in Information Retrieval.New York:ACM Press,2013:73-82. [7]Reafee W, Salim N, Khan A. The power of implicit social relation in rating prediction of social recommender systems[J].PLoS ONE,2016,11(5):e0154848. [8]Li Weimin, Zhou Xiaokang, Shimizu S, et al. Personalization recommendation algorithm based on trust correlation degree and matrix factorization[J].IEEE Access,2019,7:45451-45459. [9]Ahmadian S, Joorabloo N, Jalili M, et al. A social recommender system based on reliable implicit relationships[J].Knowledge-Based Systems,2020,192(3):105371. [10]Koren Y, Bell R, Volinsky C. Matrix factorization techniques for re-commender systems[J].Computer,2009,42(8):30-37. [11]Kong Yixiu, Hu Yizhong, Zhang Xinyu, et al. Structural centrality of networks can improve the diffusion-based recommendation algorithm[J/OL].Frontiers in Physics,2022,10.http://doi.org/10.3389/fphy.2022.1018781. [12]余文婷,吳云,林建.融合多模态自监督图学习的视频推荐模型[J].计算机应用研究,2023,40(6):1679-1685.(Yu Wenting, Wu Yun, Lin Jian. Self-supervised graph learning of fusing multi-modal for video recommendation model[J].Application Research of Computers,2023,40(6):1679-1685.) [13]Zhang Mengqi, Wu Shu, Gao Meng, et al. Personalized graph neural networks with attention mechanism for session-aware recommendation[J].IEEE Trans on Knowledge and Data Engineering,2022,34(8):3946-3957. [14]Liu Huiting, Guo Lingling, Li Peipei, et al. Collaborative filtering with a deep adversarial and attention network for cross-domain recommendation[J].Information Sciences,2021,565(7):370-389. [15]Pan Yiteng, He Fazhi, Yu Haiping. A correlative denoising autoencoder to model social influence for top-N recommender system[J].Frontiers of Computer Science,2020,14(3):article No.143301. [16]Ma Hao, Yang Haixuan, Lyu M R, et al. SoRec: social recommendation using probabilistic matrix factorization[C]//Proc of the 17th ACM Conference on Information and Knowledge Management.New York:ACM Press,2008:931-940. [17]Yang Bo, Lei Yu, Liu Jiming, et al. Social collaborative filtering by trust[J].IEEE Trans on Pattern Analysis and Machine Intelligence,2017,39(8):1633-1647. [18]Guo Guibing, Zhang Jie, Yorke-Smith N. TrustSVD: collaborative filtering with both the explicit and implicit influence of user trust and of item ratings[C]//Proc of the 29th AAAI Conference on Artificial Intelligence.Palo Alto,CA:AAAI Press,2015:123-129. [19]Jamali M, Ester M. A matrix factorization technique with trust propagation for recommendation in social networks[C]//Proc of the 4th ACM Conference on Recommender Systems.New York:ACM Press,2010:135-142. [20]Ma Hao, King I, Lyu M R. Learning to recommend with social trust ensemble[C]//Proc of the 32nd International ACM SIGIR Confe-rence on Research and Development in Information Retrieval.New York:ACM Press,2009:203-210. [21]Ma Hao, Zhou Dengyong, Liu Chao, et al. Recommender systems with social regularization[C]//Proc of the 4th ACM International Conference on Web Search and Data Mining.New York:ACM Press,2011:287-296. [22]Zhao Tong, Mcauley J, King I. Leveraging social connections to improve personalized ranking for collaborative filtering[C]//Proc of the 23rd ACM International Conference on Information and Knowledge Management.New York:ACM Press,2014:261-270. [23]Yu Junliang, Gao Min, Li Jundong, et al. Adaptive implicit friends identification over heterogeneous network for social recommendation[C]//Proc of the 27th ACM International Conference on Information and Knowledge Management.New York:ACM Press,2018:357-366. [24]Tang Jiliang, Wang Suhang, Hu Xia, et al. Recommendation with social dimensions[C]//Proc of the 30th AAAI Conference on Artificial Intelligence.Palo Alto,CA:AAAI Press,2016:251-257. [25]Chen Jiawei, Feng Yan, Ester M, et al. Modeling users exposure with social knowledge influence and consumption influence for recommendation[C]//Proc of the 27th ACM International Conference on Information and Knowledge Management.New York:ACM Press,2018:953-962. [26]Ahmadian S, Afsharchi M, Meghdadi M. An effective social recommendation method based on user reputation model and rating profile enhancement[J].Journal of Information Science,2019,45(5):607-642. [27]Liu Huafeng, Jing Liping, Yu Jian, et al. Social recommendation with learning personal and social latent factors[J].IEEE Trans on Knowledge and Data Engineering,2019,33(7):2956-2970. [28]Al-Sabaawi A M A, Karacan H, Yenice Y E. Exploiting implicit social relationships via dimension reduction to improve recommendation system performance[J].PLoS ONE,2020,15(4):e0231457. [29]Duan Zhenchun, Xu Weihong, Chen Yuantao, et al. ETBRec: a novel recommendation algorithm combining the double influence of trust relationship and expert users[J].Applied Intelligence,2022,52(1):282-294. [30]Weng Lijuan, Zhang Qishan, Lin Zhibin, et al. Harnessing heterogeneous social networks for better recommendations:a grey relational analysis approach[J].Expert Systems with Applications,2021,174(7):114771. [31]Amer A A, Abdalla H I, Nguyen L. Enhancing recommendation systems performance using highly-effective similarity measures[J].Knowledge-Based Systems,2021,217(4):106842. [32]Guo Junpeng, Deng Jiangzhou, Ran Xun, et al. An efficient and accurate recommendation strategy using degree classification criteria for item-based collaborative filtering[J].Expert Systems with Applications,2021,164(2):113756. [33]Kim J, Guo Tao, Feng Kaiyu, et al. Densely connected user community and location cluster search in location-based social networks[C]//Proc of the 29th ACM SIGMOD International Conference on Management of Data.New York:ACM Press,2020:2199-2209. [34]Koren Y. Factorization meets the neighborhood: a multifaceted collaborative filtering model[C]//Proc of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining.New York:ACM Press,2008:426-434. [35]Lee J, Noh G, Oh H, et al. Trustor clustering with an improved recommender system based on social relationships[J].Information Systems,2018,77(9):118-128.
