集总与多体耦合人车模型的振动特性仿真

李敏，李丽君，孟德世

(山东理工大学 交通与车辆工程学院，山东 淄博 255049)

汽车乘坐舒适性已经成为人们最关注的汽车性能之一。汽车振动往往会导致驾驶疲劳,长期处于这种状态下会影响驾驶员以及乘员的工作效率,强烈的振动甚至会引起职业病,造成腰椎损伤等。汽车乘坐舒适性主要根据驾驶员以及乘员的主观感受进行评价,研究驾乘人员的振动特性有助于车辆乘坐舒适性的设计和开发。

目前,国内外在人车系统耦合振动研究方面已经取得了大量的研究成果。张鄂等[1]建立了九自由度集总参数人-车系统动力学模型,分析了不同路面和车速下人体各部位的振动响应。张功学等[2]在Simulink中建立了十一自由度人-车-路系统仿真模型,对不同车速和不同位置的人体振动响应进行了仿真分析。Sezgin等[3]将十一自由度坐姿人体集总参数模型与七自由度整车模型耦合建模,分析了主、被动车辆悬架对人体振动产生的影响。Panta等[4]开发了一个十七自由度的人椅系统集总参数模型,并将其与七自由度小型汽车模型相耦合,通过特征值分析,计算了人体不同部位的固有频率。在过去的研究中,大多数研究者建立的是人车振动系统的集总参数模型,对人体多体动力学模型与汽车集总参数模型耦合建模的研究不多。

为了准确分析汽车行驶过程中驾乘人员承受全身振动的状态,本文建立集总参数与多体耦合人-椅-车动力学仿真模型来模拟实际振动环境中人体对机械振动的响应,结合在MATLAB/Simulink中建立的随机路面时域激励,通过计算加速度均方根值对人体动态乘坐舒适性进行评价。

1 坐姿人体动力学模型研究

人体本身是一个复杂的力学结构系统,更是一个复杂的振动系统。为了更好地研究驾乘人员的振动情况,研究者们提出了不同的坐姿人体生物动力学模型,主要分为集总参数模型、多体动力学模型和有限元模型[5]。集总参数模型[6-7]由质量、弹簧和阻尼器构成,可以基本满足对坐姿人体垂向振动的研究,建模简单、易于分析,但是只能用于一维分析,并不能全面反映出人体各个部位的振动响应。典型坐姿人体集总参数模型如图1所示。

(a) 三自由度模型 (b) Wan经典四自由度模型图1 典型坐姿人体集总参数模型

多体动力学模型[8-9]将人体各个部位看作相互独立的刚体,多个刚体之间通过关节(旋转和平移弹簧阻尼元件)连接,与集总参数模型相比可以模拟多个方向的人体旋转和平移运动,与车-椅系统连接能够分析人体对车辆各自由度振动的响应,能更准确地反应人体的振动特性。

2 集总与多体耦合人车模型分析

2.1 坐姿人体多体动力学模型

ISO 5982—2001[10]给出了坐姿人体振动响应的3个评价指标,分别是视在质量、座椅-头部传递函数和驱动点机械阻抗,这3个生物振动力学响应函数能很好地表达坐姿人体垂向振动特性。

视在质量为驱动点周期性激励力与其振动加速度响应的复数比值,即

(1)

式中:F(jω)为振动激励点的作用力,a(jω)为同一点作用力方向的加速度。

驱动点机械阻抗为周期性激励力与激励点速度的复数比值,即

(2)

式中v(jω)为同一点作用力方向的速度。

座椅-人体头部传递函数为人体头部响应与输入激励的复数无量纲比值,可以是位移比、速度比或加速度比,即

(3)

式中:x(jω)、x0(jω)分别为输出、输入位移,v(jω)、v0(jω)分别为输出、输入速度,a(jω)、a0(jω)分别为输出、输入加速度。

本文采用Kim等[11]的二维坐姿人体多体动力学模型进行研究,模型由头部、躯干、内脏、骨盆、大腿和小腿构成,如图2所示。通过COMSOL软件的多体动力学模块建立的坐姿人体三维模型如图3所示,设置约束使大腿质量m1、骨盆质量m2、躯干质量m3、头部质量m4具有3个自由度,分别是沿x方向、z方向的平动和绕y轴的转动,内脏质量m5不允许转动,分别通过水平和垂直的弹簧阻尼器连接到躯干和骨盆,其他各部位之间以及人体与座椅之间通过带有平移和旋转弹簧阻尼的弹性关节连接。

图2 Kim坐姿人体模型 图3 坐姿人体三维模型

根据评价指标对所建坐姿人体模型进行频域仿真计算,得到了0.5～20 Hz频率范围内坐姿人体模型的视在质量和座椅-头部传递函数曲线,如图4和图5所示。

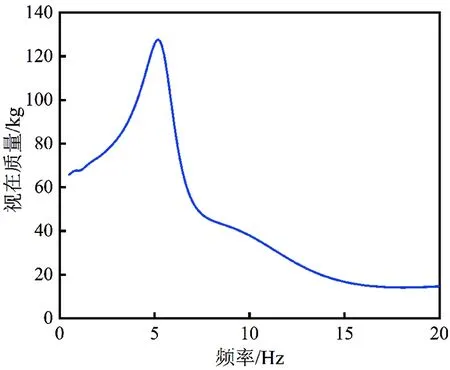
图4 坐姿人体模型的视在质量曲线

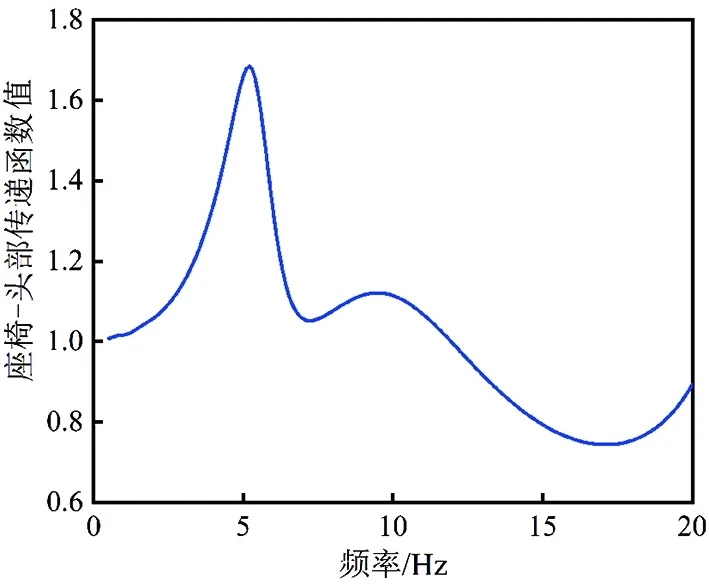
图5 座椅-头部传递函数曲线

由图4和图5可以看出,坐姿人体模型对低频振动更为敏感,该坐姿人体模型的一阶共振频率出现在5 Hz左右,二阶共振频率出现在10 Hz左右,与ISO 5982-2001标准提供的实验结果以及其他研究人员的研究结果基本一致,证明了该坐姿人体模型建模的准确性。

2.2 人-椅-车振动系统模型

为了进一步研究驾驶员以及乘客的乘坐舒适性,本文将多体动力学坐姿人体模型与车-椅模型耦合建模来分析坐姿人体在垂直、水平振动下的生物动力学响应。

车辆模型选取四自由度半车模型,将车身和车轮视为刚体,车身具有垂直和俯仰2个自由度,每个车轮具有1个垂向自由度。汽车座椅具有垂直和水平2个方向的平移自由度,通过座椅悬架连接到汽车地板上。所建模型包括车辆、座椅和坐姿人体模型在内,共具有20个自由度。在软件中对车-椅模型的车身、座椅质量部分采用多体动力学模块建模,其余部分采用集总参数模块建模,通过外部源节点连接两个物理场。建立的集总参数与多体耦合人-椅-车系统动力学模型如图6所示,人-椅-车模型的仿真计算参数见表1。

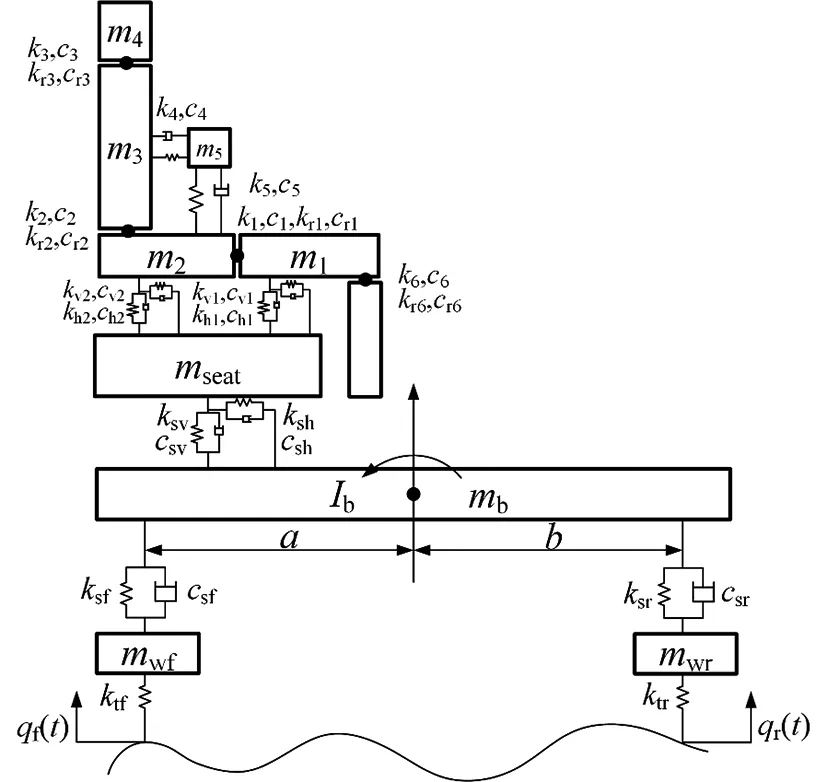
图6 集总与多体耦合人-椅-车系统动力学模型

图6中:m1、m2、m3、m4、m5分别为人体的大腿、骨盆、躯干、头部和内脏质量;k1、c1、kr1、cr1,k2、c2、kr2、cr2,k3、c3、kr3、cr3,k6、c6、kr6、cr6分别为人体各个部位关节连接处的平移和旋转弹簧刚度、阻尼;k4、c4,k5、c5分别为内脏与躯干、骨盆连接的刚度和阻尼;kv1、cv1、kh1、ch1、kv2、cv2、kh2、ch2分别为大腿和盆骨在座椅连接处的垂直、水平刚度和阻尼;mseat、mb、mwf、mwr、Ib分别为座椅质量、车身质量、前轮质量、后轮质量和车身转动惯量;ksv、csv、ksh、csh分别为座椅的垂向、水平刚度和阻尼;a、b分别为车身质心到前轴、后轴的距离;ksf、csf、ksr、csr,分别为前、后悬架的刚度和阻尼;ktf、ktr分别为前、后轮的刚度;qf(t)、qr(t)分别为前后轮路面不平度激励。

2.3 路面随机激励时域模型

路面不平度作为主要的车辆振动输入,与车辆行驶平顺性以及驾驶员的乘坐舒适性密切相关,路面模型的准确性直接影响对车辆行驶平顺性的分析。目前主要的随机路面激励时域模型生成方法有滤波白噪声生成法、谐波叠加法、Fourier逆变换法、随机序列生成法、AR法等[12]。滤波白噪声生成法计算简单、意义清楚,可以直接根据路面功率谱数值和行驶车速确定路面模型参数[13],应用较为广泛。

单轮滤波白噪声随机路面输入时域模型的计算公式为[14]

(4)

式中:n00为下截止空间频率,n00=0.011 m-1;n0为参考空间频率,n0=0.1 m-1;Gq(n0)为路面不平度系数;q(t)为路面不平度函数;W(t)为均值为0的Gauss白噪声;u为行驶车速。

在车辆沿直线匀速行驶、汽车前后轮距不变的情况下,同侧车轮后轮激励相较于前轮激励有一个时间延迟,前、后轮迟滞关系为[15]

τ=L/u,

(5)

式中:τ为相对滞后时间,L为汽车轴距,u为行驶车速。

前后轮路面激励关系为

qr(t)=qf(t-τ),

(6)

式中qf(t)、qr(t)为同一轮迹前、后轮路面激励。

根据式(4)和式(6),在MATLAB/Simulink中搭建前后轮路面时域仿真模型。据统计,我国路面不平度程度分为8级,高等级公路路面谱基本在B、C、D 3级路面范围之内。以B级路面为例,路面不平度系数Gq(n0)为64×10-6m3,车速u为40 km/h,轴距L为2.76 m,仿真时间为30 s,前、后车轮路面激励时域模型仿真结果如图7所示,车速为40 km/h时不同路面等级下的前轮路面随机输入仿真结果如图8所示。

图7 前、后车轮路面激励仿真结果

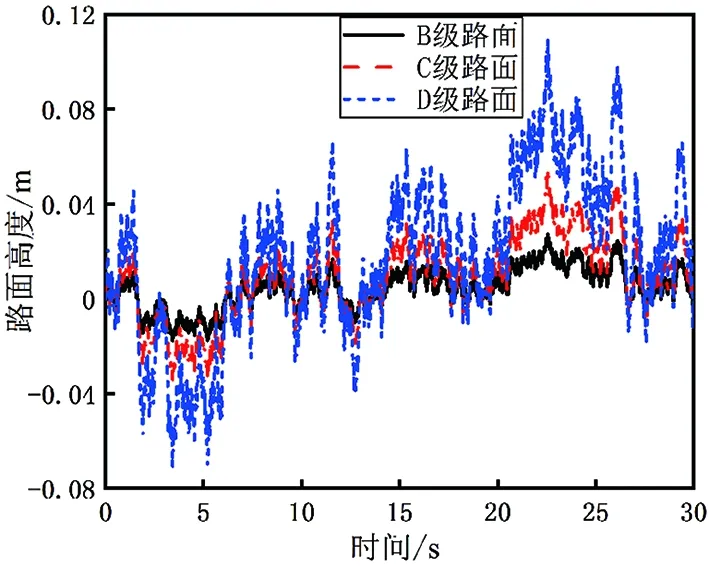
图8 3种随机路面的前轮输入仿真结果

2.4 时域、频域人体动力学响应

在COMSOL软件中,对随机路面输入下的人-椅-车系统进行时域瞬态仿真计算,设置仿真步长为0.001 s,仿真时间30 s,得到图9、图10所示车速为40 km/h时,B、C、D级路面下人体头部垂向和纵向的时域加速度响应。

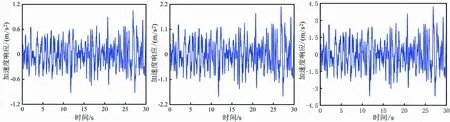
(a) B级路面 (b) C级路面 (c) D级路面图9 头部垂向加速度响应

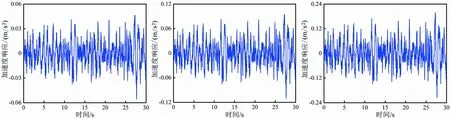
(a) B级路面 (b) C级路面 (c) D级路面图10 头部纵向加速度响应

由图9和图10可以看出,在车速一样的情况下,路面等级越低,人体头部的加速度响应幅值越大。说明路面越粗糙,越容易引起不舒适。通过对比垂向和纵向的加速度响应发现,人体头部垂向加速度幅值比纵向加速度幅值大,在随机路面激励下,人体头部运动以垂向运动为主运动,以纵向运动为次运动。

对人-椅-车振动系统进行频谱分析,将获得的人体头部时域加速度响应进行离散傅里叶变换,得到不同路面等级和车速下的加速度幅频特性曲线。图11、图12分别为车速为40 km/h时,B、C、D级路面下人体头部垂向和纵向加速度幅频特性曲线。

(a) B级路面 (b) C级路面 (c) D级路面图11 头部垂向加速度幅频特性

(a) B级路面 (b) C级路面 (c) D级路面图12 头部纵向加速度幅频特性

由图11、图12可以看出,路面不平度激励引起的人体垂向、纵向振动响应均发生在1～15 Hz低频范围内。对于垂向振动,人体头部的振动主频率分别发生在1 Hz和3 Hz左右;对于纵向振动,大约在1～3 Hz左右出现一阶共振,在6～10 Hz出现二阶共振。

3 乘坐舒适性评价

ISO 2631-1:1997(E)标准规定,当振动波形峰值系数<9时,用加权加速度均方根值来评价振动对人体乘坐舒适性的影响[16]。加权加速度均方根值可以由频域积分法求出,根据随机过程理论,某一时域信号的均方根值等于其功率谱密度函数在整个频

率范围内积分的开方值,即

(7)

式中:w2(f)为各轴向频率加权函数,Ga(f)为加速度时间历程的功率谱密度函数。

垂向、纵向频率加权函数分别为:

(8)

(9)

考虑不同轴向振动时,通过计算总加权加速度均方根值a来评价人体乘坐舒适性。

(10)

式中ax、ay、az分别为x、y、z轴的加权加速度均方根值。

通过对人-椅-车系统模型进行计算,得到了B、C、D级路面下,车速分别为40、60、80 km/h时,9种组合工况下的人体振动响应,得到了人体头部和臀部的垂向、纵向加速度均方根值(表2),并根据加速度均方根值、加权振级以及人的主观感受之间的关系评价人体乘坐舒适性。

表2 人体承受振动时的主观感受和垂向加速度均方根值

从计算结果发现,人体乘坐舒适性受到路面等级和车速的影响。C级路面下,车速由40 km/h增加到80 km/h时,随着车速的增加,人体加速度均方根值也不断增大。当车速为60 km/h时,随着路面等级降低,人体乘坐舒适性从没有不舒适状态逐渐转变为不舒适状态。说明车速越高、路面等级越低,人的乘坐舒适性越差,这与汽车实际行驶情况一致。此外,在相同行驶工况下,人体臀部总加权加速度均方根值比头部略大,垂向加速度均方根值大于纵向加速度均方根值。

4 结论

1)通过COMSOL软件建立了集总参数与多体耦合人-椅-车仿真模型,这种建模方法保证了人体建模的精度,降低了汽车建模计算的复杂程度。

2)计算了垂向、纵向人体头部和臀部的加速度均方根值,结果表明,路面等级越低,车速越高,人体乘坐舒适性越差。相较于车速变化, 由路面等级变化引起的人体头部和臀部加速度均方根值的变化率更高,因此路面等级对人体振动响应的影响更为显著。