Cahn-Hilliard方程的一个超紧致有限差分格式

栗雪娟，王丹

(西安建筑科技大学 理学院，陕西 西安 710055)

本文考虑的四阶Cahn-Hilliard方程为

(1)

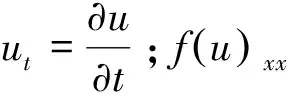
1958年,Cahn和Hilliard提出Cahn-Hilliard方程,该方程最早被用来描述在温度降低时两种均匀的混合物所发生的相分离现象。随着学者对该方程的研究越来越深入,该方程的应用也越来越广泛,特别是在材料科学和物理学等领域中有广泛的应用[1-3]。

Cahn-Hilliard方程的数值解法目前已有很多研究,文献[4]使用了全离散有限元方法,文献[5]使用了一类二阶稳定的Crank-Nicolson/Adams-Bashforth离散化的一致性有限元逼近方法,文献[6-7]使用了有限元方法,文献[8]使用了不连续伽辽金有限元方法,文献[9]使用了Cahn-Hilliard方程的完全离散谱格式,文献[10]使用了高阶超紧致有限差分方法,文献[11]使用了高阶优化组合型紧致有限差分方法。

综上所述,本文拟对Cahn-Hilliard方程构造一种新的超紧致差分格式,将空间组合型超紧致差分方法和修正的时间四阶Runge-Kutta方法相结合,求解Cahn-Hilliard方程的数值解,得到相对于现有广义格式精度更高的数值求解格式,并对组合型超紧致差分格式进行误差估计,最后通过数值算例验证该方法的可行性。

1 高阶精度数值求解方法

1.1 空间组合型超紧致差分格式

早期的紧致差分格式是在Hermite多项式的基础上构造而来的,Hermite多项式中连续三个节点的一阶导数、二阶导数和函数值的数值关系可以表示为

(2)

1998年,Krishnan提出如下紧致差分格式:

(3)

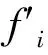
式(2)对应f(x)展开以xi为邻域的泰勒级数为

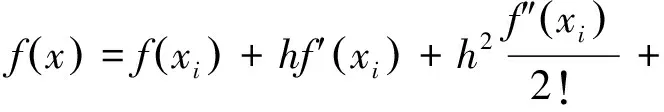
(4)

差分格式的各项系数由式(3)决定,可得到如下的三点六阶超紧致差分格式:

(5)

为优化三点六阶紧致差分格式,并保持较好的数值频散,将迎风机制[12]引入式(5),构造出如下三点五阶迎风型超紧致差分格式:

(6)

左右边界可达到三阶精度紧致格式:

(7)

(8)

上述组合型超紧致差分格式只需要相邻的三个节点便可以同时求得一阶导数和二阶导数的五阶精度近似值,比普通差分格式的节点更少,降低了计算量。

为便于编程计算,将上述构造的组合型超紧致差分格式重写为矩阵表达形式。假设U为位移矩阵,其大小为m×n,则求一阶导数和二阶导数的离散过程可以用矩阵运算表示为

AF=BU,

(9)

结合内点的三点五阶迎风型超紧致差分格式和边界点的三点三阶差分格式,组成式(9)中等式左边的矩阵A和等式右边的矩阵B,大小分别为2m×2n和2m×n;F为奇数行为空间一阶导数和偶数行为空间二阶导数组成的矩阵,大小为2m×n。以上矩阵分别为:

(10)

(11)

(12)

(13)

由式(9)可得

F=A-1BU。

(14)

解线性代数方程组(9)可得Cahn-Hilliard方程的空间一阶导数和二阶导数。对于四阶导数,可将已求得的二阶导数替代式(14)中的U,再次使用式(14)进行求取。

1.2 时间离散格式

在对很多偏微分方程的数值求解中不仅需要高精度的空间离散格式,同时还需要高精度的时间离散格式。普通的一阶精度时间离散格式显然满足不了高精度计算要求,因此本文选用时间四阶Runge-Kutta格式进行时间离散。Runge-Kutta方法是基于欧拉方法改进后的求解偏微分方程的常用方法,这种方法不仅计算效率高,而且稳定性好。格式的推算过程如下:

假设求解方程为

(15)

式中F是对空间变量的微分算子,则修正的四阶Runge-Kutta格式为

(16)

1.3 误差估计

(17)

将式(17)代入式(6),所求得组合型超紧致差分格式的一阶导数及二阶导数对应的截断误差为:

(18)

(19)

使用组合型超紧致差分格式的好处是在每一个网格点上存在一个一阶和二阶连续导数的多项式。本文比较了组合型超紧致差分格式和现有广义格式的一阶导数和二阶导数的截断误差:

(20)

式中参数α,β,a,b,c在各种格式中取不同的值(表1,表2)。本文发现在各种方案中,组合型超紧致差分格式的截断误差最小。

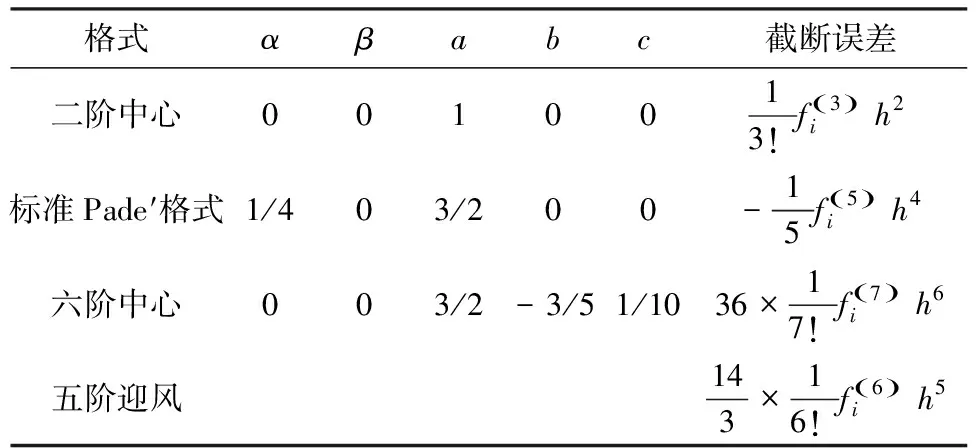
表1 不同格式一阶导数的截断误差

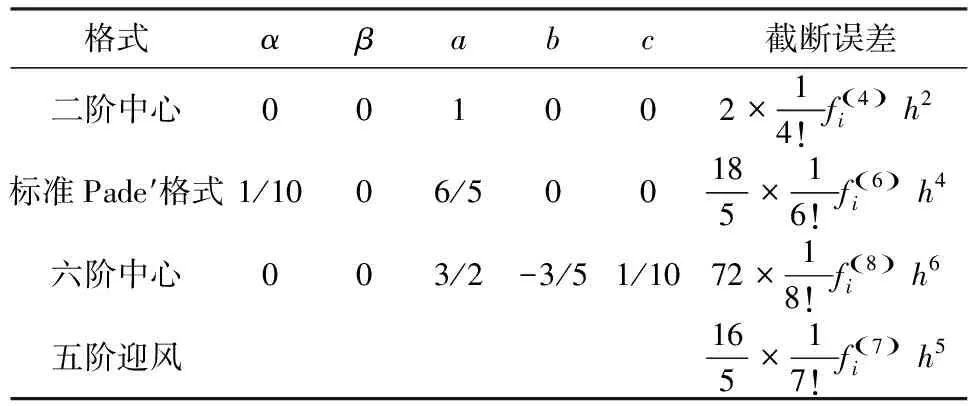
表2 不同格式二阶导数的截断误差

2 数值算例

误差范数L1和L2的定义为:

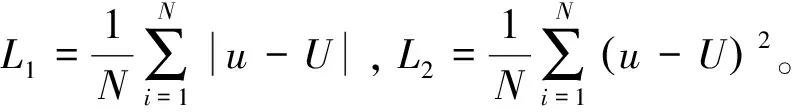
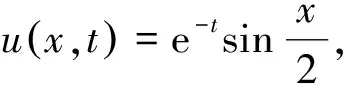
对给出的数值算例,计算误差范数L1和L2,并采用四种方法进行数值模拟,对其数值结果进行误差分析和对比,结果见表3,本文所使用方法效果最佳,由此证明所提方法的有效性和可行性。

表3 0.5 s时刻精确度测试结果(N=10)

用本文提出的式(6)—式(8)和式(16)计算算例, 图1—图3给出了不同时刻数值解与精确解的对比图,可以看出,数值解与精确解吻合很好,表明本文给出的数值格式是可行的,并且精度较高。

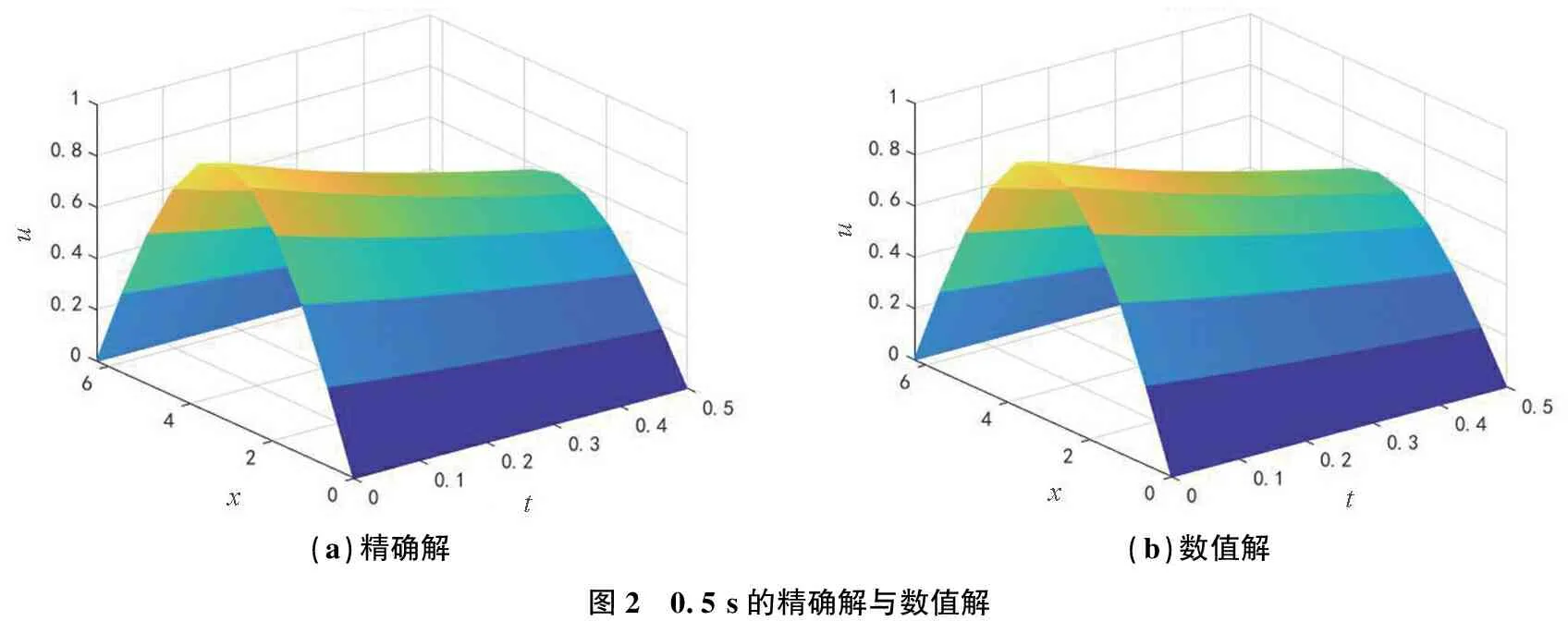
(a)精确解(b)数值解图2 0.5 s的精确解与数值解

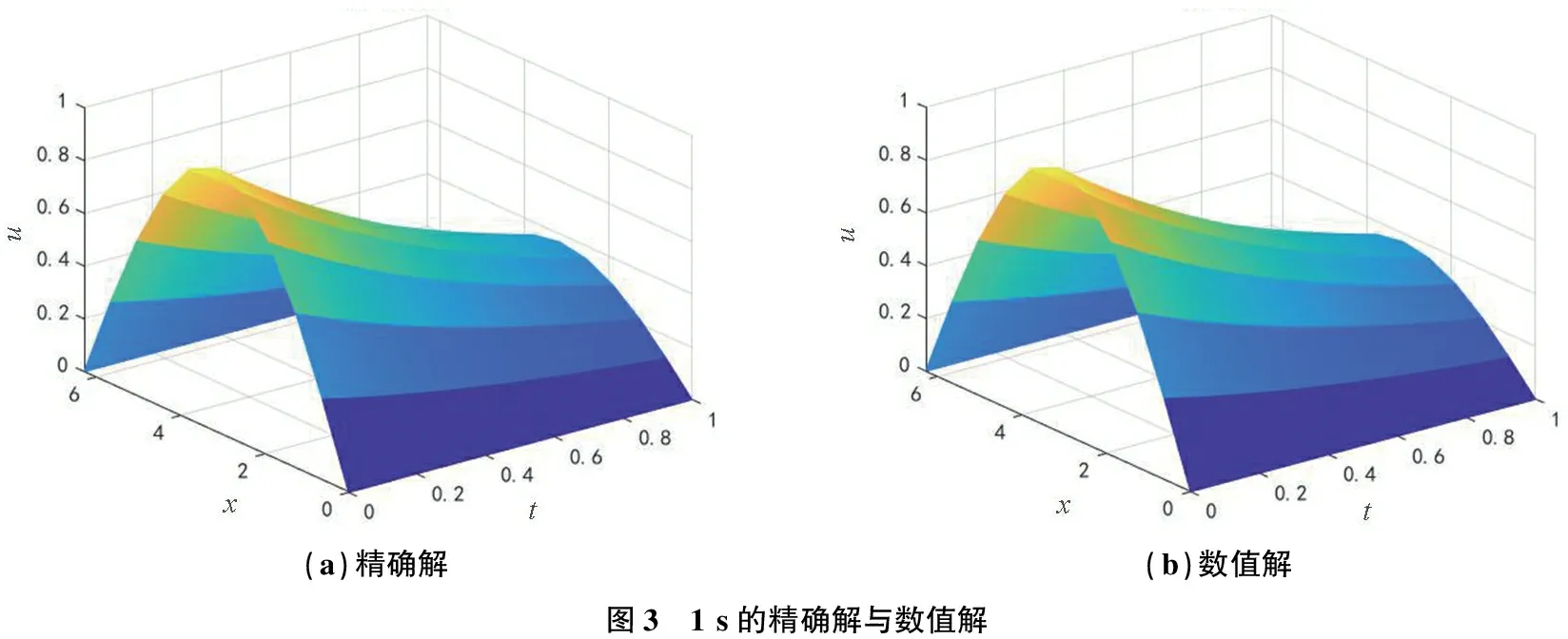
(a)精确解(b)数值解图3 1 s的精确解与数值解

3 结论

本文研究了组合型超紧致差分方法和四阶Runge-Kutta方法,并将其运用于四阶Cahn-Hilliard方程的数值求解,通过研究与分析,得到如下结论:

1)使用泰勒级数展开锁定差分格式系数,得到本文的组合型超紧致差分格式精度更高,误差更小。

2)在边界点处有效地达到了降阶,并提高了精度。

3)通过数值算例验证了数值格式的有效性。

4)预估该方法可应用于高阶偏微分方程的数值求解。