Boubaker多项式配置法求解混合线性积分方程
2024-02-06杨谨僮
杨谨僮
(西华师范大学 数学与信息学院,四川 南充 637002)
积分方程根据核函数的不同分为两大类:Volterra型和Fredholm型。在本文中讨论的是一类混合型积分,即在积分方程中包含Volterra型和Fredholm型。混合积分方程的出现来源于数学模型的建立。Kermack和McKendrick等为传染病在封闭人群中传播的时间演变提出了数学模型[1]。Thieme[2]为流行病的空间传播建立了由非线性积分方程组成的数学模型。
随着时代发展,积分方程在生物学、力学[3-10]等领域中也得到了广泛的应用。种群预测模型、生物种群生态学模型和神经脉冲传播模型也可以用积分方程表示。本文考虑了一维的线性混合积分方程,其形式如下[11]:

(1)

(2)
其中:u(x),u(h(x))是未知函数;f(x),g(x),h(x),k1(x,t),k2(x,t),k2(x,h(t))是已知函数;a,b,λ1,λ2都是常数。f:[a,b]→R,h:[a,b]→[a,∞],ki:[a,b]×[a,b]→R(i=1,2)。
很多研究者用配置法求解Volterra型积分方程和Fredholm型积分方程以及奇异积分方程的近似解。由于配置法应用范围广泛,因此也可以用于求解混合型积分方程的近似解。近年来,许多不同的函数[12-15]被用来估计积分方程的解,如2005年Yousefi等[12]人提出的勒让德小波。2011年Ezzati等[13]人提出了切比雪夫函数。2014年Mustafa等[14]人提出的拉格朗日多项式、重心的拉格朗日多项式以及修正的拉格朗日多项式三种不同的函数形式;同年,Mashayekhi等[15]人提出了伯努利多项式。根据结构的不同,形成了不同的配置法。除此之外,还有迭代法[16-17]、逼近法[18-19]、分解法[1,20-21]等多种方法求解混合型积分方程。本文提出了基于Boubaker多项式的配置方法来求解形如公式(1)和公式(2)的Volterra-Fredholme积分方程,并进行了收敛性分析。Boubaker多项式配置法的主要特点是借助Boubaker多项式将积分方程转化为代数方程组求解。
1 Boubacker多项式
给出标准的布贝克多项式的三项递归关系[2]:
B0(x)=1
B1(x)=x
B2(x)=x2+2
Bn(x)=xBn-1(x)-Bn-2(x)n≥3
(3)
其中,n是非负整数。
2 Boubaker多项式配置法
通过Boubaker多项式配置法求解混合线性积分方程的近似解,对
(4)
(5)
其中,Bi(x)和Bi(h(x))是由公式(3)定义的Boubaker多项式,bi(i=0,…,k)是未知的系数。
将公式(4)和公式(5)代入积分公式(1)和公式(2)中得:

(6)
(7)
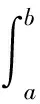
(8)
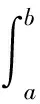
(9)
令


将公式(8)和公式(9)用矩阵的形式表示:
AB=F
(10)
CB=G
(11)
其中,矩阵A,B,C,G,F的定义如下:
A=(aij)k×k,B=(b1,b2,…,bk)T,C=(cij)k×k,G=(g(x1),g(x2),…,g(xk))T,F=(f(x1),f(x2),…,f(xk))T
求解线性代数方程,得到系数b1,b2,…,bk从而得到公式(1)和公式(2)的近似解。
3 算例

3.1 算例1
求解形如公式(1)的混合线性积分方程[7]
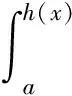
的近似解,f(x)=h2(x)-4ex+ex+1+ex-h2(h2(x)+2h(x)+2),k1(x,t)=ex-t,k2(x,t)=ex+t,λ1=1,λ2=-1,h(x)=x2,a=0,b=1。算例1中Boubaker多项式配置法与其他方法误差对比如表1所示。通过表1的结果可以看出,本文提出的Boubaker多项式配置法中,随着n增大,所得到的近似解与精确解之间的误差逐渐缩小,但是当n取2时,与其他方法相比,该效果较差;随着n增大,其他的两种方法求得的误差几乎没有变化,甚至当n取4时,拉格朗日多项式配置法得到近似解与精确解之间的误差反而增大了。
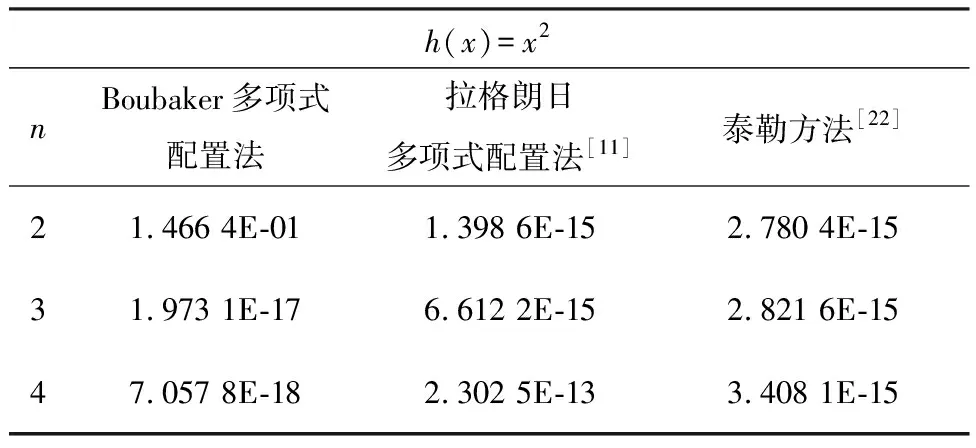
表1 算例1中Boubaker多项式配置法与其他方法误差对比
3.2 算例2
求解形如公式(2)的混合线性积分方程

的近似解,其中g(x)=e-x-ex(h(x)-1)跟,k1(x,t)=ex+t,k2(x,t)=ex+h(t),λ1=1,λ2=-1,a=0,b=1。算例2中Boubaker多项式配置法与其他方法误差对比如表2所示。通过表2的结果可以看出,随着n增大,三种方法所得到的近似解与精确解之间的误差都在逐渐缩小。当n取2时,与其他方法相比,Boubaker多项式配置法效果一般,当n取8时,其效果也比其他两种方法好。

表2 算例2中Boubaker多项式配置法与其他方法误差对比
4 结论
本文提出了求解一维混合线性积分方程的Boubaker多项式配置方法。通过算例误差分析验证了该方法的可行性和有效性。结合算例1和算例2的误差分析,表明该方法效果较好。
