LCL型并网逆变器电网电压前馈控制策略研究

薛荣辉

(西安航空学院 电子工程学院,西安 710077)

0 引言

我国将在2030年实现碳达峰,2060年实现碳中和,从电力领域来看,新能源发电逐步替代常规能源发电是实现“双碳”目标的重要途径之一[1-2]。

近年来,虽然风能和太阳能发电占比逐渐提高[3-4],但是风能和太阳能发电具有间歇性的特点,产生的电力不能直接满足负载的要求,需通过电力电子装置进行控制变换。此外,随着科技的发展,对电力电子装置的要求也越来越高。为减少并网电流谐波污染电网,达到并网要求,一般并网逆变器采用滤波器进行滤波。尽管LCL型滤波器性能优于L型滤波器,但在频率响应时会出现谐振尖峰导致谐振频率也跟着发生跳变,若不加入有效阻尼就会导致并网逆变器的输出产生振荡使系统不稳定[5]。

为减轻电网电压产生的谐波对并网电流的影响,通常采用LCL型滤波器。一般情况下,该型滤波器对电网产生的谐波抑制能力还有待提高。文献[6]研究表明,采用电容电流反馈有源阻尼可以有效抑制滤波器的谐振尖峰。

随着并网功率的提高,单台逆变器不能满足要求,需多台逆变器并联运行,导致电网呈现弱电网特性,电网阻抗对系统产生影响[7]。文献[8]提出改进型电网电压前馈控制,采用微分近似控制器代替全前馈的微分项,解决部分前馈误差。文献[9]在电压前馈通道中串联相角补偿函数来解决相位偏移问题,采用基于虚拟电感的电网电压前馈控制来提高系统对弱电网的适应能力。本文借鉴前述工作,引入电容电流有源阻尼,采用电容电流反馈有源阻尼控制,利用电网电压前馈控制策略,分析电压前馈和电容有源阻尼系数对并网电流的影响,建立仿真模型进行分析。

1 单相并网逆变器模型

图1所示为LCL型单相并网逆变器主电路拓扑结构,图中:Vin为直流侧输入电压;Vinv为逆变器输出电压;i1为逆变器输出电流;ic为电容支路电流;i2为并网电流;Hi1为电容电流反馈系数;Hi2为电网电流反馈系数;Hv为电网电压反馈系数;L1表示逆变器侧电感;C为滤波电容;L2为并网侧的电感。通过PLL锁相环产生跟踪电网电压Vg相位,得到相位θ,构成并网电流的有效指令。在控制电路中,Gi(s)为电流调节器,采用PI调节器。

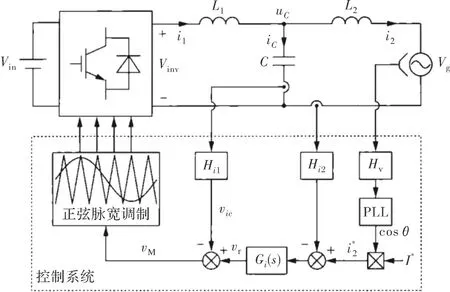
图1 单相LCL型并网逆变器拓扑结构

电容电流反馈的有源阻尼数学模型控制框图如图2所示,根据参考文献[6]对图2数学模型进行变换得到图3所示。

图2 采用电容电流反馈有源阻尼数学模型框图

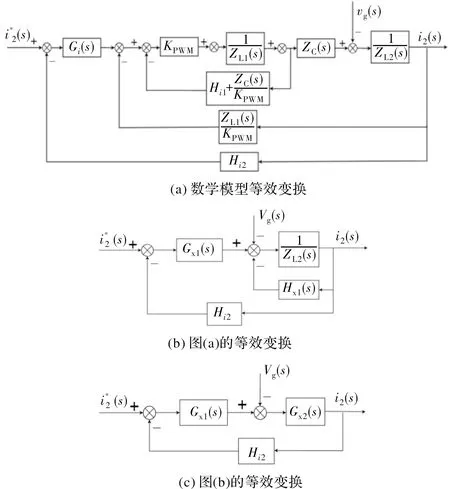
图3 数学模型等效变化过程

图3为数学模型等效变化过程。通过比较点和交叉点移动等效变换得到图3(c),由此可得传递函数(式(1)和(2))。

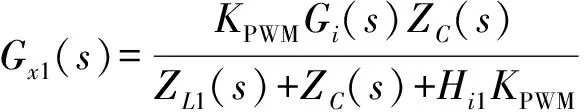
(1)

(2)

Gx2(s)=

(3)

(4)

环路增益的表达式为:

TA(s)=Gx1(s)Gx2(s)Hi2

(5)

并网电流i2(s)的表达式为:

=i21(s)+i22(s)

(6)

式(1)～(6)中KPWM为逆变器传递函数;Hi1为电容电流反馈系数;Hi2为电网电流反馈系数;Hv为电网电压反馈系数;Gi(s)为电流调节器;ZL1(s)、ZL2(s)、Zc(s)分别表示电感L1、L2、电容C的阻抗;i21(s)为并网电流指令跟踪分量;i22(s)为电网电压引起的并网电流扰动分量。

由式(6)可知,并网电流i2由稳态分量和电网电压引起的扰动分量构成。当电网电压存在背景谐波时,并网电流i2畸变现象是因为随着扰动分量所占比例的增加而改变的,所以可通过电网电压前馈控制降低扰动分量,提高并网电流质量。

2 电网电压前馈控制

由图3可知,在并网逆变器的输出端口处并联了一个大小相同的Gx2(s)/(1+TA(s))导纳,可以完全的抑制Vg(s)对并网电流i2(s)产生的干扰。等效于在电网电压的扰动Vg处与并网电流i2之间引入一条正向通道传递函数为Gx2(s)的支路,如图4所示。

图4 电网电压全前馈框图

将图4进一步等效变化,得到图5,再将扰动分量Vg的前馈相加点从Gx2(s)的输出端向前移动到Gx1(s)的输出端处,并在此处添加一个反馈点,依据自控前馈点前移的原理改变其前馈函数,等效变换如图6(a)所示,等效变换后的结构如图6(b)所示。

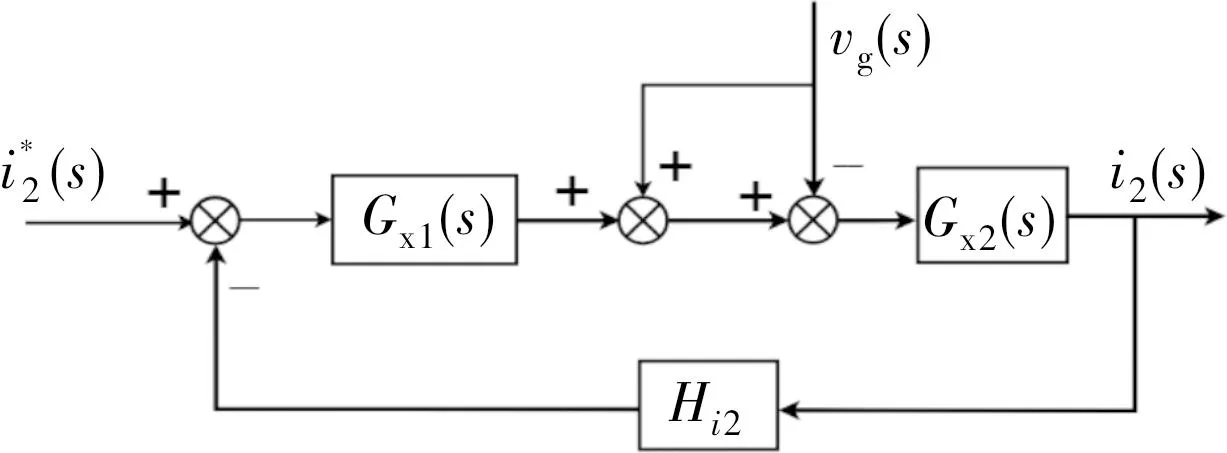
图5 电网电压全前馈等效变化框图

图6 全前馈等效变换框图

由图5和6得到电网电压前馈传递函数Gff(s)[10]

(7)

式中:1/KPWM为比例项;CHi1s为一次微分项;(L1C/KPWM)s2为二次微分项[6]。

3 非理想条件下电网电压前馈

3.1 比例前馈函数项

将s=j2πf代入式(4),可得

Gff_P(j2πf)+Gff_d(j2πf)+Gff_dd(j2πf)

(8)

由式(8)得其中全前馈的比例项为

(9)

当选取全前馈函数Gff(j2πf)的幅值为基准时,得到的误差E1(j2πf)的幅值标幺值用E1(P,u)表示,其表达式为

(10)

当E1(P,u)(f)<0.1时,根据式(6)可以求出fp1≈181 Hz。电网电压前馈函数当只有比例项时可以抑制3次谐波以下,此时的谐波抑制能力与全前馈抑制能力相当。

3.2 比例+一次微分前馈函数项

只采用比例前馈加一次微分时,产生误差用E2(j2πf)表示,产生误差E2(j2πf)的幅值标幺值E2(P,u)的表达式为

(11)

当E2(P,u)(f)<0.1时,根据式(7)可以求出fp2≈641 Hz。当含有13次以下谐波时,采用比例加一次微分前馈项可以达到谐波抑制,且与全前馈的抑制能力相似。但当存在的谐波数量超过13次时,无法抑制谐波。采用全前馈可以使幅值标幺值为0,因此,采用全前馈函数可以完全有效消除电网电压包含50次以下谐波对并网电流的影响[11]。

4 仿真验证

为了验证前馈控制策略的可行性,在MATLAB/Simulink平台搭建仿真模型,仿真条件如表1所示。

表1 电网电压前馈仿真参数

4.1 电网电压比例前馈

强电网忽略电网阻抗(Lg=0),建立图7所示的单相LCL型并网逆变器MATLAB/Simulink仿真模型图。

图7 单相LCL并网逆变器全前馈仿真模型

采用电容电流有源阻尼反馈,电网电流反馈,电网电压经PLL锁相环得到电网电流给定电流,电网电压前馈环节包括比例前馈、一次微分前馈、全前馈三部分,对不同的方法进行多次的仿真与比较分析。

通过0.02 s在电网电压注入10%的3次谐波,验证比例前馈作用。图8所示为计算所得电网电压加入3次谐波各前馈环节并网电流。

图8 电网电压加入3次谐波各前馈环节并网电流

由图8(a)～(d)四张波形对比,并网电流波形相似,通过THD分析,无前馈时ig畸变率是5.37%,比例前馈、比例+一次前馈、全前馈时ig畸变率是2.30%左右,满足并网要求。所以当电网含有3次谐波时,通过引入比例前馈可以实现消除电网电压带来的谐波。

4.2 电网电压比例+一次微分前馈

通过0.02 s在电网电压注入10%的3、5、7、9次谐波,5%的11、13次谐波,验证比例+一次微分前馈作用。图9所示为计算所得电网电压加入13次谐波各前馈环节并网电流。

图9 电网电压加入13次以下谐波各前馈环节并网电流

由图9(a)～(d)四张波形对比,从图(a)可以看出无前馈时并网电流畸变严重,THD为25%,加入比例前馈ig畸变率是6.53%,加入比例+一次前馈ig畸变率是2.77%、全前馈时ig畸变率是2.42%,所以当电网含有13次以下谐波时,通过引入比例+一次微分前馈可以实现消除电网电压带来的谐波。

4.3 电网电压全前馈

通过0.02 s在电网电压注入10%的3、5、7和9次谐波,5%的11、13、15、17和19次谐波,3%的21、23、25、27、29、31和33次谐波验证全前馈作用。图10所示为计算所得电网电压加入33次谐波各前馈环节并网电流。

图10 电网电压加入33次以下谐波并网电流

由图10(a)～(d)四张波形对比,从图(a)可以看出无前馈时并网电流畸变严重,THD为37.52%,加入比例前馈ig畸变率是21.35%,加入比例+一次前馈ig畸变率是10.73%、全前馈时ig畸变率是2.59%,所以当电网含有33次以下谐波时,通过引入全前馈可以实现消除电网电压带来的谐波问题。

5 结论

本文研究了并网逆变器电网电压前馈控制。首先,建立LCL并网逆变器数学模型。其次,依据电网电压对并网电流产生干扰的现象对有源阻尼数学模型图进行框图等效变化。最后,提出电网电压全前馈方法是为了验证理论分析并且可以完全有效地达到抑制电网电压对并网电流产生影响的效果。通过MATLAB的Simulink对此次实验进行仿真运行,所得结论如下:

(1)若谐波次数为3次时,比例前馈可以有效地抑制对并网电流产生的干扰现象;

(2)若谐波次数为13次以内时,比例加一次微分前馈可以抑制对并网电流的影响;

(3)若谐波次数存在13次以上时,要想达到有效抑制干扰现象的效果只能采用电网电压全前馈;

(4)谐波次数不同时都能不同程度地抑制电网电压,但起到的作用各不相同。