MCI的rs-fMRI功能性连接的特征选择与压缩

晏 洁,吴海锋,,保 涵

(1.云南民族大学 电气信息工程学院,云南 昆明 650500;2.云南民族大学 云南省高校智能传感网络及信息系统科技创新团队,云南 昆明 650500)

近年来,静息态核磁共振成像(rest-state functional magnetic resonance imaging,rs-fMRI)因其无创性、高分辨率且具有较好的安全性的特点,已普遍应用于脑部疾病的诊断[1-3].已有研究表明,轻度认知障碍(mild cognitive impairment,MCI)一种功能性连接(functional connectivity,FC)丧失症,表现为患者某些大脑区域的网络连通性显著下降.通过rs-fMRI可以很方便地构建脑区网络,从而评判患者脑区网络的连通性[4-6].采用rs-fMRI构建脑区网络的方法主要有相关法[7-9]、图论[10]以及格兰杰因果分析(GCA)[11]等,其中皮尔逊相关是一种常用方法.研究大脑的动态变化时[12],可计算其加窗皮尔逊相关[13]建立动态功能网络连接(dynamic functional connectivity,DFC).然而,无论皮尔逊相关还是加窗皮尔逊相关,若大脑感兴趣区(region of interest,ROI)数目较多,计算的相关系数数量将非常庞大,如何从这些庞大的相关系数中提取有效的特征来评判脑区间的连通性是一件较困难的工作.由于个体的差异,每个被试的脑区连通性不尽相同,同时,所计算的相关系数的数量庞大也会产生一些冗余信息,这些因素都增加了评判脑区连通性的难度.

随着计算机技术的快速发展,机器学习(machine learning,ML)已逐渐地成为了一种辅助的医学诊断方式[14-15],其本质是利用分类器对两类或两类以上的对象进行分类.在ML中,分类器性能依赖于所提取的特征,可表达组间显著性差异的特征将会得到较高的分类准确率.虽然将脑区连通性作为分类器的特征输入[16]是近年来常用的一种分类方法,但如前所述,如何从庞大的特征提取有效特征仍是一项挑战.另外,即使提取出有效特征,特征的数目仍然巨大,如何进行降维,避免维度诅咒[17]也是采用ML实现分类需要解决的一个问题.

针对以上问题,本文做了如下工作：第一,对由rs-fMRI所计算的加窗皮尔逊相关系数进行特征选择,通过计算最小类内距离,筛选出更有效的特征.第二,对选择后的特征通过最小二乘(least square,LS)拟合的方式进行数据压缩,减小了特征维度.实验采用一组公开的MCI和正常对照(normal control,NC)组来进行分类,将经过特征选择和特征压缩的数据作为分类器的输入.实验结果表明,经处理后特征的分类准确率比未经处理特征的分类准确率要高8%.

1 相关工作

对于rs-fMRI信号,最常用的分析技术是基于种子的分析 (SBA)[18-19],其定义的种子点可将大脑划分为116个ROI的自动解刨标记(anatomical automatic labeling,AAL)[20].通过AAL提取的数据维度本身较大,若再计算DFC,产生的数据不仅包含FC信息,还包含时间信息,数据量会更大,这会增加计算复杂度,导致信息冗余,故可采取特征选择的方法.通常,特征选择方法可分为3类：过滤法[21]、包装法[22]和嵌入法[23].过滤法通过统计单变量的特征的基本属性,设定阈值选择特征.包装法直接利用最终分类器的性能来评估特征选择和分类的总体效果,需要多次交叉验证来训练分类器,花费时间较多,但有比过滤法更准确的分类结果[24].然而,由于使用的交叉验证,包装法可能在不同的分类数据上选择不同的特征[25].嵌入法与过滤法类似,但是它的特征选择过程与分类器训练有关[26],又因为该方法没有对特征子集进行迭代评估,所以比包装法的计算速度更快,但占用的计算资源较大.

较多的特征数不仅包含冗余信息,还易造成维度灾难问题[27],因此降维对分类具有重要意义.主成分分析(principal component analysis,PCA)是一种用于降低特征维数的技术,其不仅被成功地用于描述疾病相关空间模式的生物学过程[28-29],还可提取神经影像分类中的有效特征[30-31].然而,使用PCA降维的特征与原始特征的物理性质没有直接联系,这使得分类的可解释性变得复杂.线性判别分析(LDA)[32]试图通过寻找在高斯分布假设下最大化类可分性的线性投影来消除PCA的这一缺点.然而,无论是PCA还是LDA都不可避免的丢失了数据信息,是一种有损的数据降维方式.多元分类和回归分析也可实现降维,在多元分类和回归分析中,最常使用线性模型分析特定区域与认知功能之间的相关性[33-35],其新特征集是原始特征的线性组合,因此降维后的数据可无损地恢复成原始数据.遗憾的是,这方面研究分析通常依靠先验选,或者需要分析MCI和NC受试者的结构连接模式差异,这给实际应用带来了一定困难.

2 方法

2.1 总体框架

首先对符合标准的rs-fMRI数据进行预处理,再通过AAL模板提取ROI的血氧水平依赖(blood oxygen level dependent,BOLD)信号,计算BOLD信号间的加窗皮尔逊相关系数得到DFC(由于DFC相关矩阵为对称阵,故只需取其上三角部分即可),其次利用训练样本中的最小类内距离准则选取合适的特征数目,然后对筛选后的数据进行LS线性拟合,最后将得到的拟合系数作为支持向量机(support vector machine,SVM)分类器的特征输入,其总体框架如图1所示.下面,将对上述步骤做更详细介绍.

图1 系统框图

2.2 加窗皮尔逊相关

根据k折交叉验证,将所有被试者组成的集合N划分为两个子集XS和XT,使其满足

XS∪XT=N&XS∩XT=0&XS/XT=1-1/k.

(1)

若将xnj∈RT×K表示为将第j类的第n个被试的ROI时间序列矩阵,其中T表示时间点数,K表示ROI数目,则对该矩阵计算第w个时间窗口的皮尔逊相关系数后将得到矩阵

(2)

其中w=1,2…W,j=1,2,…,J.

2.3 特征选择

(a) 最小类内距离

最小类内距离指两个类中距离最小的作为两类距离,反之,最大类间表示两个类中距离最大的作为两类距离.先计算训练集的总体类内距离,得到

(3)

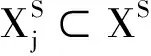
(4)

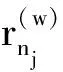
(5)

Y=[r(p1),r(p2),...r(pM)].

(6)

(7)

J类训练集的组平均特征所构成的矩阵就为

Δ=[A1,A2,…AJ].

(8)

(b)最大类间距离

计算类间距离,得到

(9)

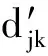
(10)

与(5)同理,在组平均上也可得I个δ′,令其为δ′(i),由最大类间距离准则所选择的M个特征的位置可计算为

(11)

剩余步骤与最小类内距离准则一样.

2.4 特征压缩

即使经过特征选择后,特征数目依旧庞大,为了避免维度诅咒问题,我们采用LS特征压缩,即将每一被试经特征选择后的DFC矢量表达为聚类中心的线性组合(聚类中心由J类训练集的组平均特征所构成),通过LS拟合求解该线性组合.将一被试者的特征选择矢量表达为

Y=Δθ+ε.

(12)

其中,ε表示误差矢量.根据LS估计求解,可得最后的压缩系数

(13)

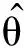
最后,将θn表示为第n个被试的特征压缩矢量,将其与标签ln构成一个元胞

Zn=<θn,ln>.

(14)

根据n所属的集合,组成最终的训练集S和测试集T.上述计算步骤如下所示.

step 2：划分集合,对DPABI预处理后的图像划分为训练集XS和测试集XT;

step 3：在集合XS中,根据(3)(9)分别获得最小类内距离和最大类间距离δ;

step 4：通过(5-11)筛选M个最小类内距离和最大类间对应的位置,并分别将其位置带入(7)得到Aj;

step 5：将J类训练集的组平均特征作为聚类中心,得到Δ;

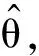
3 实验

3.1 实验设置

本实验所用rs-fMRI数据采用自阿尔茨海默病神经影像学数据库(alzheimer’s disease neuroimaging initiative,ADNI),参数设置如表1.

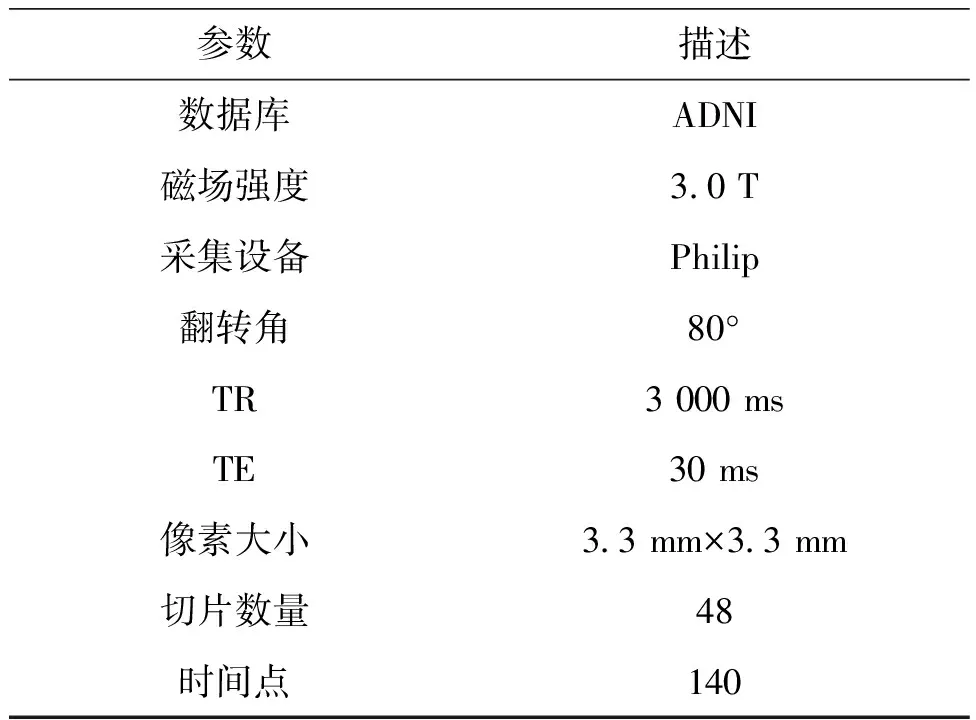
表1 rs-fMRI数据参数设置

该实验使用数据处理和脑成像分析(data processing &analysis of brain imaging,DPABI)工具箱[36]进行数据预处理,下载地址为：http：//rfmri.org/dpabi,处理步骤如下：

● 默认去除原始数据前10帧图像,以使图像稳定;

● 时间层矫正,以第48个切片为基准使每个切片上的数据具有相同时间点;

● 手动调整被试图像,使其与标准图像位置保持一致,再将结构像配到功能像,然后把结构像分割成灰质、白质和脑脊液;

● 控制生理噪声(包括全局信号、灰质白质中的噪声等)和去除线性漂移;

● 校正所有被试者的头部运动,采用Friston 24头动参数模型(包括3个转动参数和3个平动参数);

● 进行归一化和平滑,并过滤数据的频率范围为

● 0.01～0.08 Hz,以此滤除低频偏移和高频噪声;

● 使用AAL地图集识别ROI;

● 再次调整头动,设置头动排除标准：大于 2 mm 位移和2°旋转角度;

● 筛选配准质量好的结构像与功能像,最后获得32个MCI和32个NC图像.

本文采用SVM来评估我们方法的分类性能.由于样本数量有限,采用五折交叉验证,同时,为避免交叉验证结果的偶然性,重复上述步骤十次,最后结果取平均.为了评估特征选择和特征压缩结合方法的有效性,本文还做了以下对比试验,具体参数由表2列出,步骤简述如下：

● Pearson：计算两两ROI间BOLD信号的皮尔逊相关系数;

● WP：将时间分割成若干份(即窗口),在每个窗口独立地计算皮尔逊相关系数;

● WP-FS：对加窗皮尔逊后的数据只进行特征选择,即通过最小类内距离准则或者最大类间距离准则进行特征筛选,以此减少特征数目;

● WP-FDM：对加窗皮尔逊后的数据进行特征压缩,即通过LS对聚类中心进行线性拟合,以此降低特征维度.其中聚类中心采用有监督方式获得,即将MCI与NC的相关系数组平均分别作为聚类中心;

● P-FS-FDM：对传统皮尔逊先进行特征选择,再进行特征压缩,其中聚类中心分别为MCI与NC经特征选择后的相关系数的组平均;

● WP-FS-FDM：对加窗皮尔逊先进行特征选择,再进行特征压缩,其中其中聚类中心分别为MCI与NC经特征选择后的相关系数的组平均;

● WP-FS-FDN：对加窗皮尔逊先特征选择,后特征压缩,其中聚类中心采用无监督方式(K均值聚类)获得;

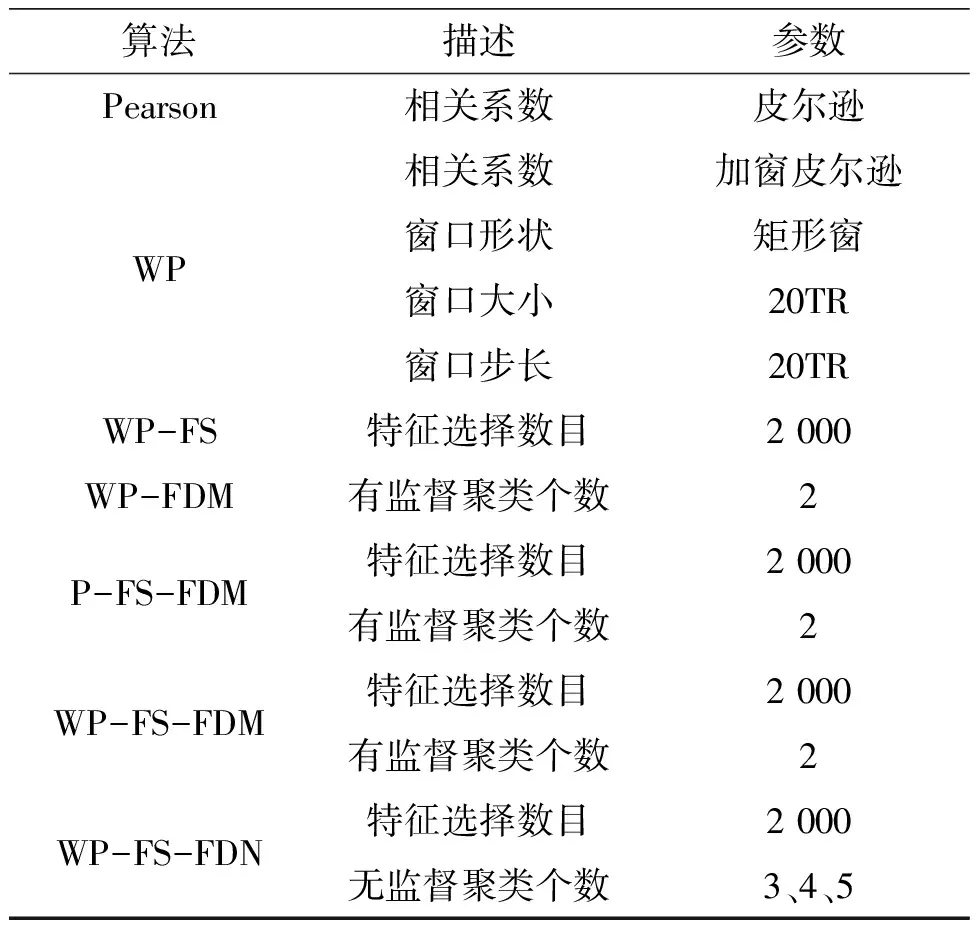
表2 各算法参数设置

3.2 实验结果

3.2.1 比较不同特征选择方法的分类性能

首先,我们比较了两种特征选择的方法(包括最小类内、最大类间)的平均分类准确度.由图2可知,两种方法分别在不同的最优值有最大的分类准确率.当特征数小于最优值时,分类准确率都随着特征数的增加而增加.当特征数大于最优值时,准确率没有进一步提高.其中,最小类内的方法在特征数目为 2 000 左右时,分类准确率最高,达到73.25%.

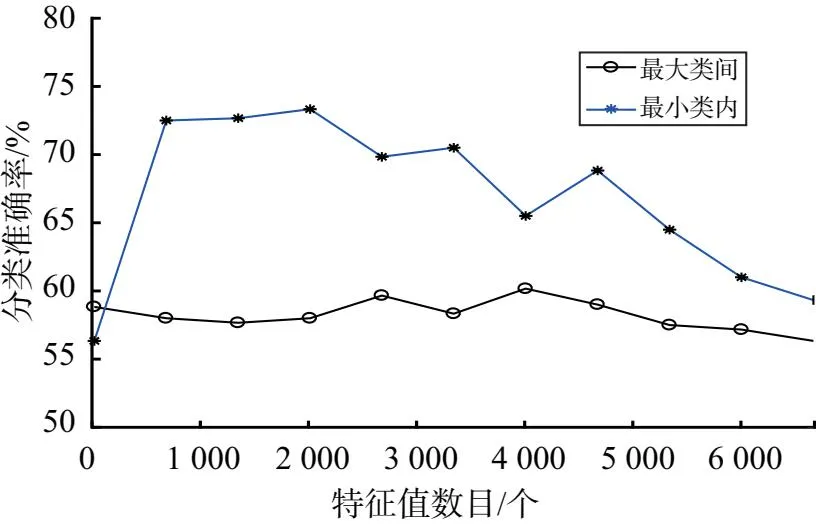
图2 不同特征选择算法分类结果

3.2.2 LS特征压缩

将被试用不同状态的线性组合来表达动态功能连接,分别得到MCI和NC两组拟合系数.如图3所示,MCI和NC的数据由于类间距离较大以及类内距离较小,故分别聚成两簇.

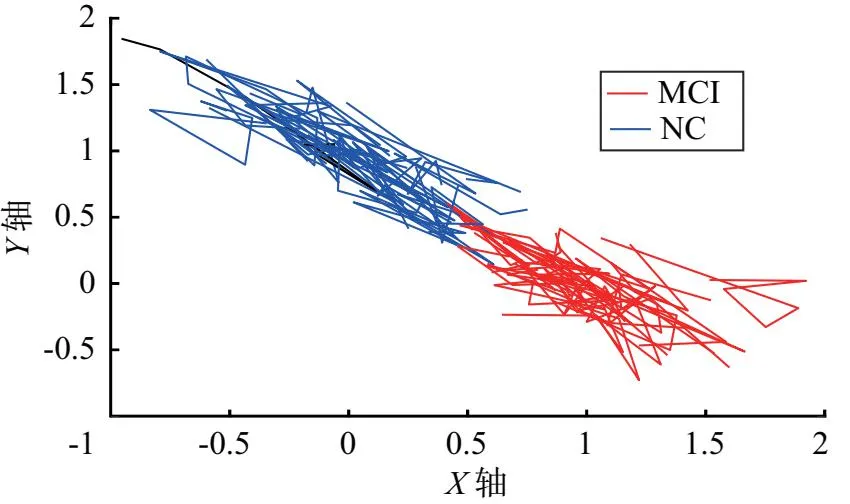
图3 拟合系数连接动态模式差异

本文将MCI和NC的DFC组平均作为聚类中心,实质是一种有监督聚类方式,为验证本文提出的算法性能,我们比较了有监督和无监督聚类的LS特征分类准确率,图4(a)为十次五折交叉验证实验的均值,图4(b)为每一次实验的结果.观察可知,采用有监督聚类的方法获得的分类性能最好,无监督聚类即便是聚5类获得了最好的分类准确率,还是远远低于有监督聚类的LS特征分类结果.

图5显示了不同算法的分类性能,图5(a)为十次五折交叉验证实验的均值,图5(b)为每一次实验的结果.从图5(a)中可以看出,本文提出的方法分类精度最高,相比传统的Pearson方法提高了大约8%,WP、WP-FS、WP-FDM以及P-FS-FDM的分类准确率分别为62%、69%、62%、72%.

为了观察特征压缩前后的数据特征,使用PCA技术将MCI和NC的样本数据投影到二维空间中便于可视化,如图6所示.一般同一类数据的特征之间具有高度相似性,易聚在一起.观察可知,在使用本文算法前,两类数据交错一体,难以分辨.算法后,两类数据分别排布在分类线两边,易于区分.

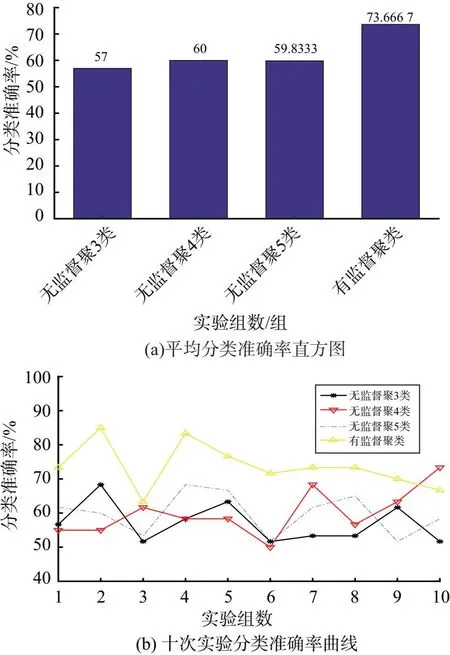
图4 有监督和无监督分类结果

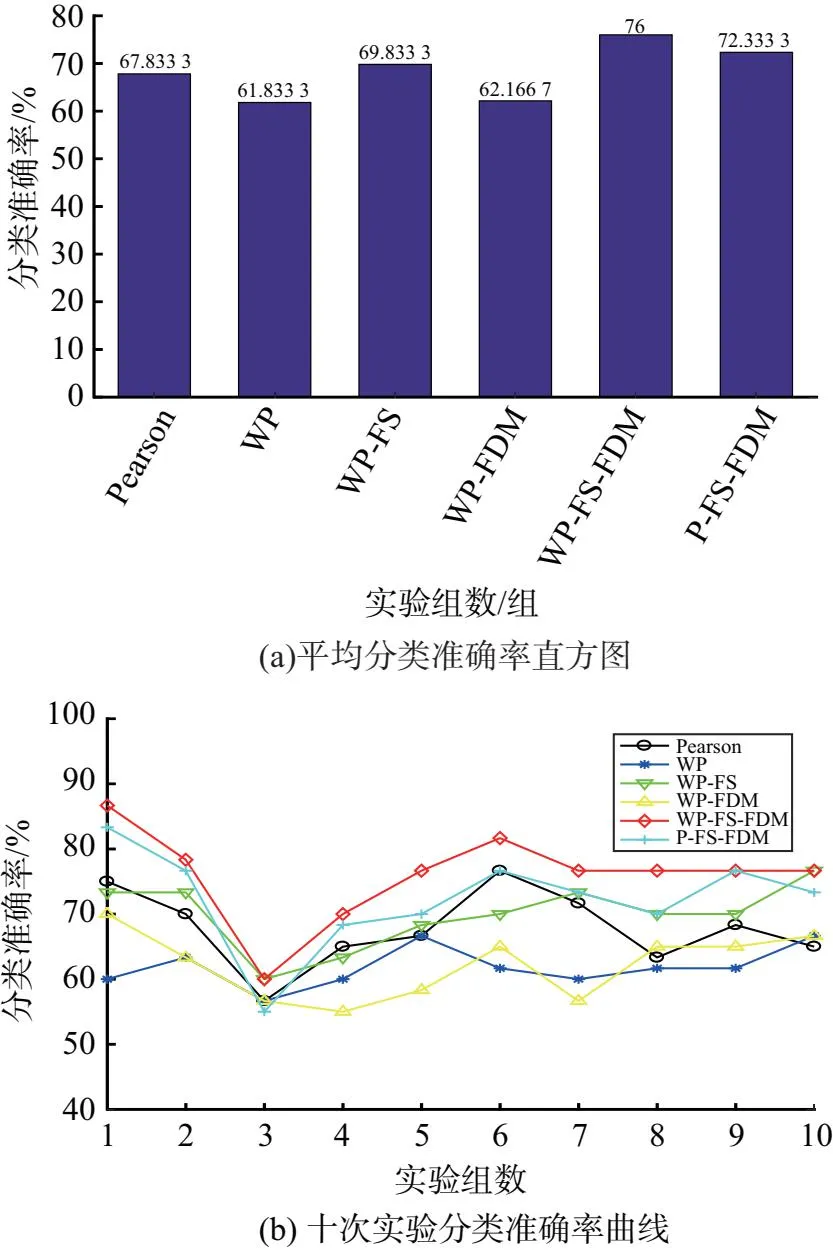
图5 组合算法分类结果

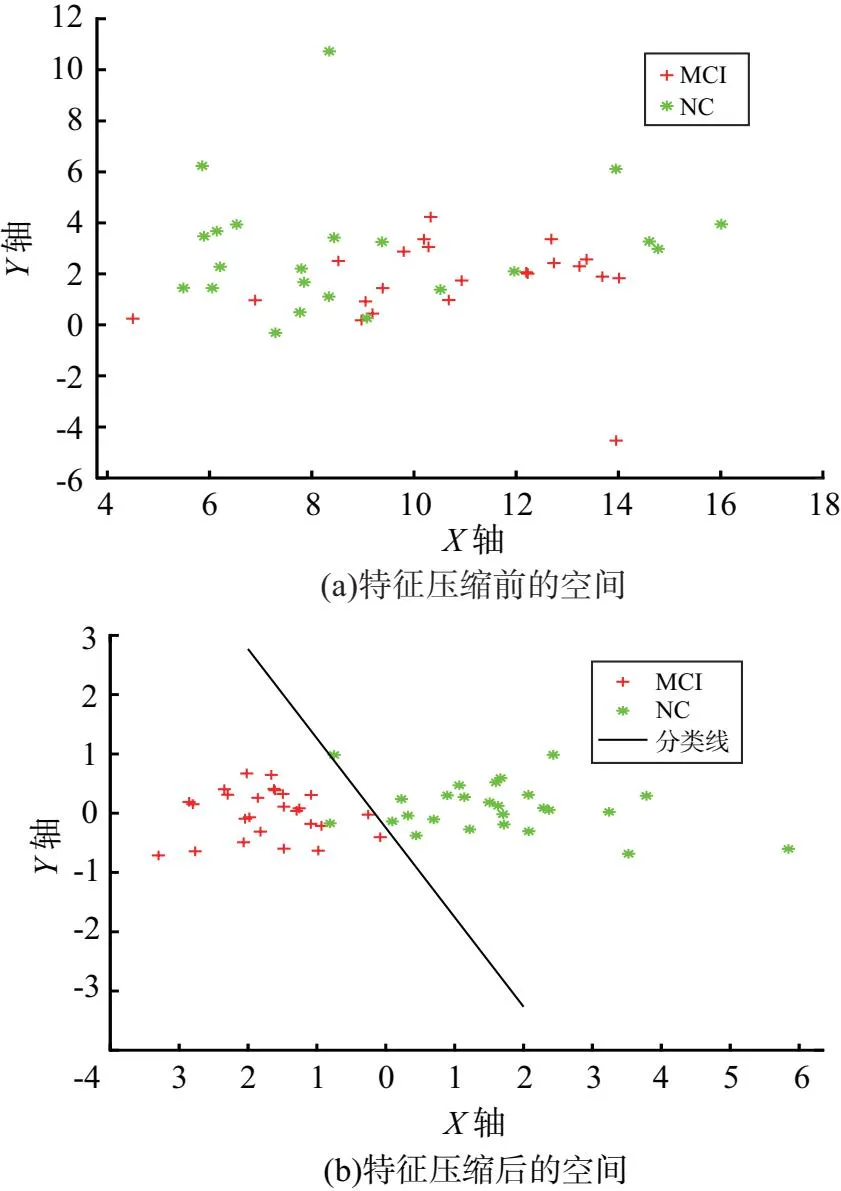
图6 二维空间中样本的分布情况

4 结语

在使用rs-fMRI数据对MCI和NC分类的研究中,用特征选择或降维来提升分类准确度是可行的,但二者的结合会得到何种结果并未得到充分的讨论.本文试图结合最小类内特征选择和LS特征降维两种方式来提高分类性能.特别地,LS降维可称之为一种特征压缩方法,因为经压缩的特征的信息损失较少,可经聚类中心重建.

本文的LS特征压缩中,一个重要步骤是聚类,而聚类又可划分为有监督聚类和无监督聚类.在传统的DFC研究中,大多采用无监督聚类,而本文采用有监督的LS特征压缩,其分类准确率比无监督聚类的分类结果上升了13%,一种可能的解释是有监督聚类的聚类簇明确.在有监督方法中,若聚2类,则一类是MCI组平均,一类是NC组平均,用该簇中心点所表达的特征就具有明确结果.例如,一个MCI被试者的特征用该簇中心来线性表达时,表达MCI簇的权重就较大,而NC的权重就较小,因为该被试的特征与MCI簇更为接近.相反,无监督聚类所获得的聚类簇并不明确,可能同时存在MCI和NC被试者的特征,用此聚类中心表达的权重的指向性就不太明确.

特征选择是筛选具有显著组间差异性的特征,而降维是减少特征维数的过程.特征降维通常会带来信息丢失,毕竟数据量经降维后会相应减少.PCA是典型的有损降维,而本文提出的LS压缩可减少信息的丢失.为了观察特征降维后的数据形态,我们分别对比了这两种算法降到二维的结果,发现经PCA降维的特征矢量在二维空间中分布较为散乱,两类数据互相交错,难以区分.另一方面,经LS压缩的特征投射至二维空间后,两类特征间的分类线可轻易找到.该结果说明,MCI和NC两类样本经LS特征压缩后比经PCA降维后更易区分,这也印证了无损的压缩可能比有损的压缩具有更好的分类性能.

在实验中,还在算法中加入加窗皮尔逊的方法,目的在于测试该方法与特征选择和压缩间可能存在的关联.首先,总体看,加窗皮尔逊经特征选择后比无窗皮尔逊的分类准确率高,这也在情理之中,毕竟加窗的方法增加了特征的动态信息.其次,加窗皮尔逊只运用特征选择或者只采用特征压缩时,分类准确率并不能达到最高,而同时选用两种方法时,分类准确率将达到最高的76%.一个合理的解释是,特征选择可能去除了冗余信息,而特征压缩消除了维度诅咒,两种方法在提高分类准确率上应该都是必须的.这也证实了本文的一种重要结论：特征选择和特征降维的结合可有效提升分类准确率.

此外,本文本应关注另一重要问题,FC的动态特性.皮尔逊相关加窗后其实已具有了动态性,但本文的重心还是在于加窗的特征维度变大后分类性能如何提高,并未对其动态性做深入研究.本文的实验结果表明,FC的特征经LS压缩后投射到低维空间呈现了运动的形态,且现有的研究已证实,MCI的FC动态性能与NC有所区别,因此,研究MCI和NC间LS压缩特征的运动特性差异也将具有积极意义.在未来的工作中,我们可尝试采用图论的方法分析LS特征压缩的时变规律,利用图密度、平均路径长度和小世界性等指标分析相关性能.