采用改进北方苍鹰算法的微电网优化调度研究
2024-02-05陈将宏王羲沐李伟亮李雪莲
陈将宏,王羲沐,李伟亮,李雪莲,袁 腾
(三峡大学 电气与新能源学院, 湖北 宜昌 443000)
0 引言
在可再生能源对电网渗透加深的背景下,分布式电源(distributed generation,DG)逐渐走进人们的视野,它能够充分利用可再生能源,有效减少碳排放,带来较好的经济效益[1-2]。而微电网作为一种新型的分布式能源组织结构,被视为整合可再生能源的有效平台,使可再生能源接入配电网更加便捷[3-4]。
微电网通常包含多种分布式电源,在构建微电网调度模型时,优化变量较多,属于非线性优化问题,故多采用智能算法进行求解[5]。常见的智能算法有差分进化算法[6](differential evolution algorithm,DE)、粒子群算法[7-8](particle swarm optimization,PSO)、乌鸦搜索算法[9](crow search algorithm,CSA)等。群智能算法大多模拟生物群体的行为,如PSO和CSA分别模拟了鸟群和乌鸦群体的觅食过程,而DE模拟的是生物群体的进化过程,这些算法利用群体信息和个体信息间的交互,促使分布在周边的个体向种群中心移动。智能算法具有较好的鲁棒性和求解精度,但在求解过程中容易陷入局部最优解而导致精度下降。在现有的研究中通常需要对算法进行改进,常使用的改进策略包括种群初始化改进[10]、混合算法[11-12]、变异[13]等。其中,种群初始化改进和变异的目的都是增加种群多样性,增强全局和局部搜索能力;而混合算法能够尽可能地发挥每种算法的优势,使其具有强的求解能力。
需求响应(demand response,DR)是电力需求侧管理的重要途径,能够缓解电力高峰供电不足的情况,促进可再生能源消纳,提高微电网的运行可靠性。将DR纳入微电网调度也是近年的热点研究方向,已有许多学者取得了一定的研究成果[14-17]。上述研究证明了DR能够有效降低发电侧的成本,使负荷侧具有更好的灵活性。现有的DR模型所用电价机制多为分时电价,其削峰填谷的能力较强,但未考虑可再生能源的出力特性,并不能实时反映发电侧的变化。
基于以上分析,为降低微电网日运行成本,将反向学习、Metropolies准则和自适应t分布变异引入北方苍鹰算法[18](northern goshawk optimization,NGO)中,提出了一种混合策略改进的NGO算法,记为HNGO;同时提出了一种基于风光电出力特性的需求响应模型,构建考虑需求响应的微电网优化调度模型,利用HNGO求解,并与DE、PSO、CSA以及NGO求解结果进行对比,结果表明所提算法具有更高的求解精度。
1 微电网模型
1.1 微电网结构
微电系统主要发电单元由风力发电机(wind driven generator,WT)、光伏列阵(photovoltaic array,PV)、小型内燃机(internal combustion engine,CE)、燃料电池(fuel cell,FC)、微型燃气轮机(micro gas turbine,MT)以及蓄电池(storage battery,BT)组成。微电网结构如图1所示。
1.2 计及风光出力特性的需求响应模型
DR主要分为激励型需求响应(incentive-based demand response,IBDR)和价格型需求响应(priced-based demand response,PBDR)2种。
1.2.1 PBDR模型
价格型需求响应通常实施分时电价来促使用户调整负荷,减少用电高峰期的负荷量,增加平谷时段的负荷量。不同类型的负荷对电价的敏感程度不同,根据文献[19]将负荷分为可转移负荷(shiftable load,SL)和可削减负荷(curtailable load,CL)。
可转移负荷是指用户根据自身需求对电价信号做出响应,引导用户将负荷从高峰时段转移到平谷时段,可用价格需求弹性矩阵来描述其变化特性。弹性矩阵E(t,l)表示t时刻负荷对l时刻的弹性系数,则需求响应后可转移负荷的变化量ΔPSL为

(1)
式中:PSL(t)为t时刻初始可转移负荷量;ESL(t,l) 为SL弹性矩阵;p1(t)为DR后t时刻的电价;p(t)为DR前t时刻的初始电价。
可削减负荷通过比较DR前后的电价来确定是否削减自身负荷。用弹性矩阵描述其变化特性,则DR后可削减负荷的变化量ΔPCL为

(2)
式中:PCL(t)为t时刻初始可削减负荷量。
1.2.2 考虑风光出力的分时电价
电价需求响应按照分时电价来引导用户,现有的分时电价策略按照用户的用电习惯,在用电高峰时段执行峰电价,其他时段执行平谷电价,但这种策略没有考虑可再生能源的波动性和出力特性,特别是在以风光电为主要供电来源的微电网系统中,并不利于可再生能源的高效利用。为此考虑风光出力的特性,将可再生能源出力大的时段设置为谷时段,总功率小的时段设置为峰时段,其余时段设置为平时段,促使用户的用电习惯靠近可再生能源的出力特性,其计算方式如下:

(3)
式中:S(t)为t时刻负荷功率与风光总出力;Smax、Smin分别为总功率的最大值和最小值;λ、γ为区间控制系数。
2 微电网优化调度模型
2.1 目标函数
设定调度周期为24 h,调度间隔为1 h,以微电网日运行成本最低为目标函数进行调度。日运行成本包括发电单元的燃料成本、设备维护成本、交互成本以及环境成本。
发电成本C1为CE、FC和MT运行过程所消耗燃料的费用:
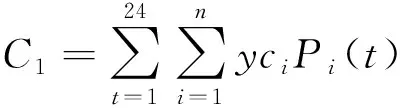
(4)
式中:Pi(t)为t时刻第i个发电单元的输出功率;ci为第i个发电单元的燃耗系数;n为发电单元的个数;y为燃料价格。
设备维护成本C2为
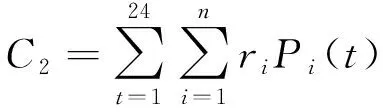
(5)
式中:ri为第i个发电单元的维护系数。
微电网与主网通过联络线相连,可以进行电能的双向传输,产生的费用即为交互成本C3:
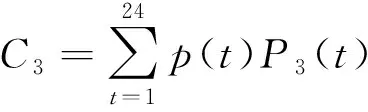
(6)
式中:P3(t)为t时刻的交互功率,大于0时表示向主网购电,小于0时表示向主网售电。
CE、FC和MT在工作过程中会排放污染物,主要包含CO2、NOx和SO2等污染气体。为了减少对环境的破坏,微电网需对污染气体进行处理,所需的费用即为环境成本C4:
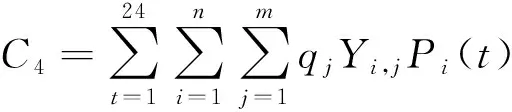
(7)
式中:qj为污染物j的单位处理成本;Yi, j为第i个发电单元对污染物j的排放系数;m为污染气体的种类。
由此可知,微电网日运行成本f为
f=C1+C2+C3+C4
(8)
2.2 约束条件
1) 功率平衡:微电网系统中总保持供需平衡。
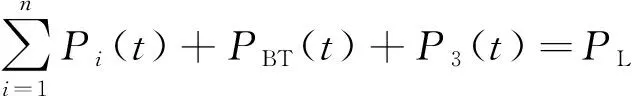
(9)
式中:PBT为蓄电池的输出功率;PL为负荷功率。
2) 微源出力限制:各个发电单元的输出功率不能超过限制。
Pi,min≤Pi≤Pi,max
(10)
式中:Pi,max和Pi,min分别为功率上限和下限。
3) 蓄电池重充放电约束:蓄电池过充、过放都会对电池的性能和容量造成损伤,因此必须限制其容量状态。
SOCmin≤SOC(t)≤SOCmax
(11)
式中:SOC(t)为t时刻蓄电池的容量状态。
3 北方苍鹰算法
3.1 标准NGO
北方苍鹰的狩猎策略分成2个阶段:第1阶段,北方苍鹰识别猎物后,以极快的速度向其靠近;第2阶段,北方苍鹰会在小范围内狩猎猎物。NGO就是基于上述狩猎行为而提出的。
在NGO中,群体中每个个体都代表一个可行解,算法开始时在搜索空间内随机初始化种群,种群X定义为

(12)
式中:Xk为第k个北方苍鹰个体;xk,d为第k个可行解的第d个变量的值;N为种群个数;D为变量维度。
NGO基于北方苍鹰的狩猎行为建立数学模型,其迭代过程可以分为2个阶段:第1阶段为识别和攻击阶段;第2阶段为逃逸和追逐阶段。
在第1阶段,北方苍鹰会随机选择1个猎物G,然后迅速攻击它。此阶段增加了NGO的全局搜索能力,能够快速靠近最优解的目标区域。这一阶段的数学模型为
G=Xs
(13)

(15)
式中:Xk为第k个可行解;Xk,1为第一阶段第k个可行解的新位置;α为[0,1]内的随机数;F为适应度函数;s为[1,N]内的随机正数;I取值为1或2。
在第2阶段,北方苍鹰在攻击猎物后,猎物会试图逃跑,北方苍鹰会持续追逐猎物。因为北方苍鹰速度极快,所以可以在任何情况下追上猎物并完成狩猎。这一阶段增强了NGO的局部搜索能力,能够快速向最优解靠近。在NGO中,假设北方苍鹰的狩猎半径为R,则该阶段的数学模型为
R=ω(1-it/Tmax)
(16)
Xk,2=Xk+R(2α-1)Xk
(17)

(18)
式中:it为当前迭代次数;Tmax为最大迭代次数;ω为步长;Xk,2为第2阶段第k个可行解的新位置。
3.2 改进NGO
NGO具有较好的求解精度和稳定性,但仍具有以下局限性:① 采用随机初始化种群,初始解分布不均匀,种群多样性不足;② 在第2阶段内,北方苍鹰快速追赶猎物,所以算法后期搜索速度很快,容易陷入局部最优解。
针对以上不足,在算法初始化阶段引入反向学习初始化种群,在第2阶段位置更新中引入Metropolies准则以增加种群多样性;在第2阶段结束后对最优个体进行变异,增强其跳出局部最优解的能力。
1) 反向学习初始化。初始种群在搜索空间内的分布对智能算法的寻优效率和寻优精度都有着直接影响。为此采用反向学习[20]来初始化种群,其表达式为
x′=l+u-x
(19)
式中:l为变量的下限;u为变量的上限。
在初始化阶段,利用随机法和反向学习生成2个不同的种群,计算其适应度,并按照适应度从小到大排列,取前1/2作为初始种群。
2) Metropolies准则。为保证种群在迭代过程中具有一定的多样性,将模拟退火算法中Metropolies准则引入NGO的第2阶段位置更新中。该准则通过概率PT来判断是否接受当前解的新位置,概率的计算公式为:
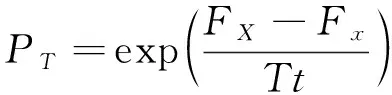
(20)
Tt=δFbest
(21)
式中:Tt为当前温度;Fbest为最优解的适应度;δ为升温系数。
利用Metropolies准则取代式(15),在位置更新后,随机生成一个[0,1]内的数,并与PT进行比较,若大于PT则接受当前解的新位置,反之不接受。
3) 最优解变异策略。变异是种群进化的重要方式,研究采用自适应t分布变异[21]对最优解进行变异,以增强其跳出局部最优解的能力。
t分布又称学生分布,其概率密度函数含有参数自由度β,曲线形状与自由度β相关,β越小则曲线越平稳。自适应t分布变异的定义为:
x′=x(1+trnd(it))
(22)
式中:x′为变异后的可行解位置;trnd( )为t分布随机数。
自适应t分布变异使用迭代次数it作为自由度参数:算法初期,自由度值较小,t分布接近柯西分布,具有较好探索性;算法后期,自由度值较大,t分布接近高斯分布,具有较优的局部收敛性。
3.3 算法时间复杂度分析
假设NGO的时间复杂度为T(n),搜索空间维度为D,北方苍鹰种群数量为N,最大迭代次数为Tmax。种群初始化的复杂度为O(N),第1阶段位置更新的复杂度为O(ND),第2阶段先计算狩猎半径再进行位置更新,其复杂度为O(ND+1),则NGO的时间复杂度为T(n)=O[Tmax(2ND+1)+N]。HNGO相较于NGO增加了反向学习、Metropolies法则、自适应t分布变异3个流程,复杂度也相应增加。反向种群初始化分别利用随机方法和反向学习生成2个不同的种群,其复杂度为O(2N);Metropolies法则嵌套在第2阶段位置更新中,其复杂度不再重复计算;自适应t分布变异的复杂度为O(D)。因此,HNGO的时间复杂度为T(n)=[2N+Tmax(2ND+D+1)],时间复杂度略有提高。
3.4 改进效果验证
为了验证所改进算法的有效性,选取了文献[18]中7个单峰函数F1—F7,3个多峰函数F8、F9和F15,共10个不同的基准函数进行实验,其数学表达式、维度以及最优值见文献[18]。选择NGO、CSA、PSO以及DE作为对照组,每种算法单独运行30次,最大迭代次数为500,求每个测试函数最优解的平均值、方差以及最小值。各算法的参数如表1所示,测试函数实验结果如表2所示。

表1 各算法参数

表2 测试函数实验结果
从表2可看到,对于单峰函数F1—F7,HGNO 3个指标均为最小,同时方差在5种算法中也最小,证明HNGO具有较好的稳定性,求解精度上领先其他4种算法30~80个数量级;对于多峰函数F8,PSO的求解精度最好,HNGO的平均值、方差以及最小值均优于NGO;HNGO和NGO都能求得函数F9的理论最优值,精度优于其他3种算法;对于函数F15,为比较各个算法跳出局部最优解的能力,设置最大迭代次数为100,比较各算法在较小迭代次数内的搜索能力,可以看到HNGO的3项标准均最小,且达到了理论最优值,证明了其具有更强的全局搜索能力。
以微电网日运行成本为种群适应度函数,利用HNGO求解微电网经济调度模型步骤如下:
1) 初始化种群规模N、最大迭代次数Tmax等参数,利用随机法和反向学习分别生成初始种群,计算2个种群适应度并进行排序,取适应度小的1/2作为初始种群;
2) 随机选择猎物,计算其适应度函数值,根据式(14)和式(15)进行第1阶段位置更新;
3) 根据式(16)计算追逐半径R,按照式(17)更新种群位置,依据Metropolies准则判断是否接受新位置;
4) 对最优个体进行t分布变异,若变异后适应度优于变异前,则保留;
5) 判断循环是否结束,若达到则输出最优解和最优位置,否则返回步骤2)。
HNGO流程如图2所示。
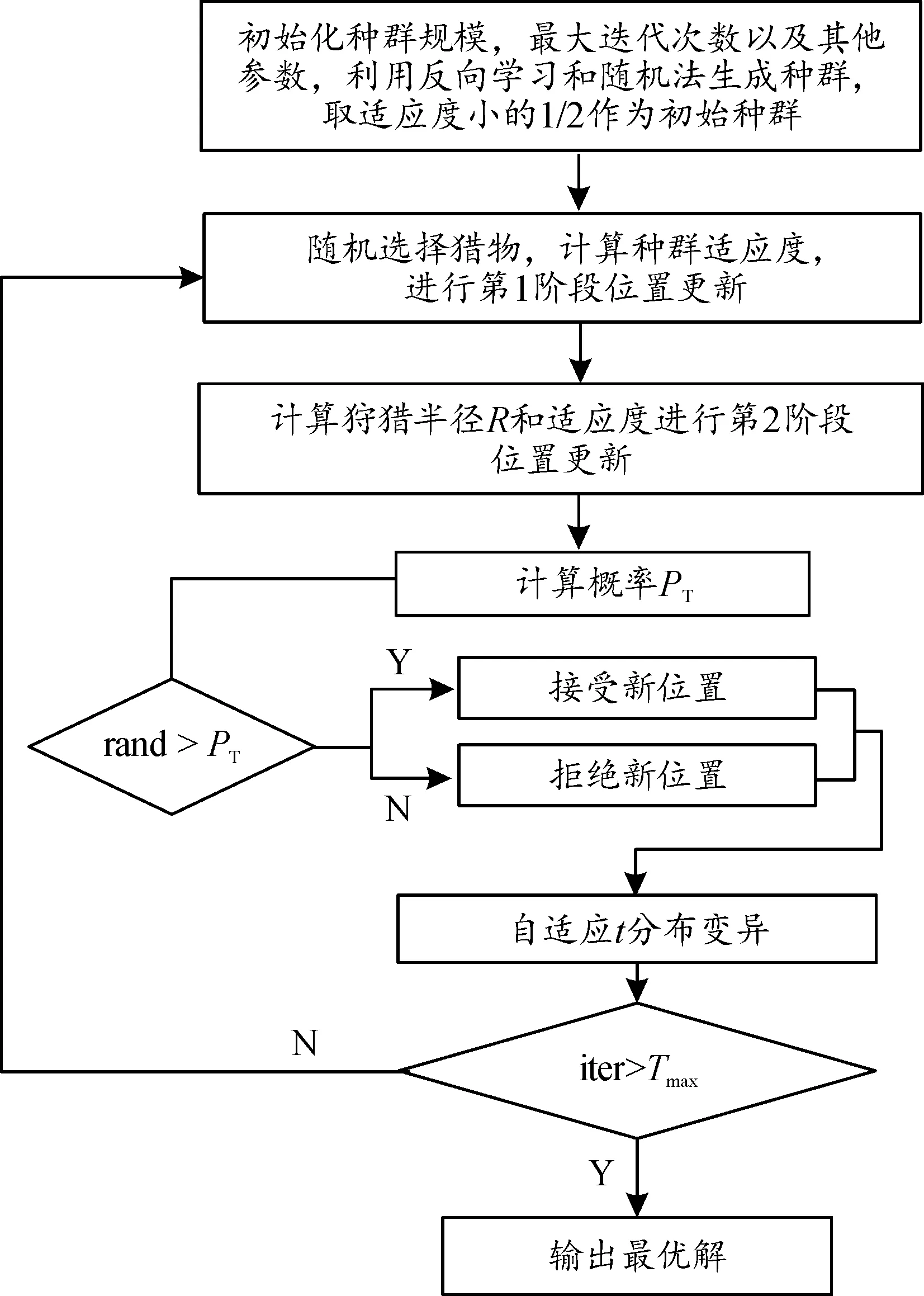
图2 HNGO流程图
4 算例分析
4.1 系统参数
按照上述分析建立微电网优化调度模型,设定微电网与主网的交互功率上限为100 kW,蓄电池SOC初始值为0.5,上、下限为0.2和0.8,天然气价格为2.55元/m3,各电源的参数如表3所示,污染物处理成本如表4所示,风光以及负荷预测功率如图3所示。
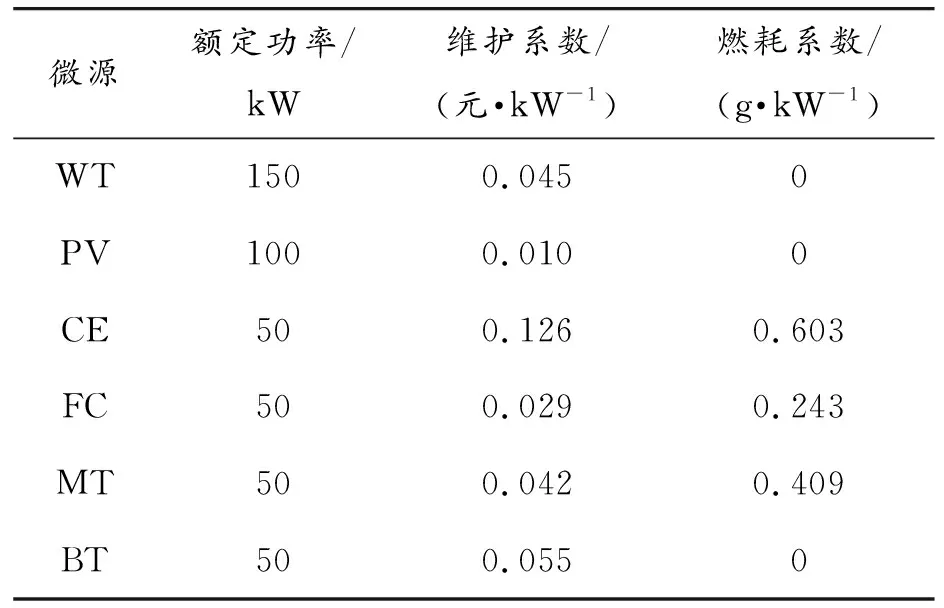
表3 电源参数

表4 污染物处理成本
设置3种场景来验证所提算法以及需求响应模型的可行性:场景1采用分时电价,不考虑DR;场景2采用分时电价DR模型;场景3采用计及风光出力特性的DR模型,区间控制系数γ=λ=0.2。其中固定负荷、可转移负荷和可削减负荷占比分别为0.6、0.2、0.2,用户电价弹性系数见文献[22]。
按照所提DR模型,得到的计及风光出力的分时电价如图4所示,3种场景下的负荷功率如图5所示。

图4 计及风光出力的分时电价
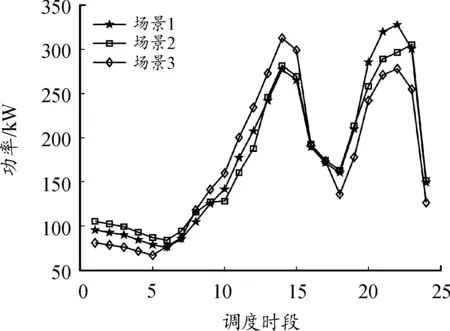
图5 3种场景下的负荷功率
从图4可以看到,考虑风光出力特性的分时电价与传统分时电价具有明显的差异,所提分时电价策略与风光总出力规律更贴近。
从图5可以看到,基于分时电价的DR削峰填谷效果更好,高峰时段负荷下降,谷时段负荷增加。而所提DR模型,在0∶00—5∶00时段,风光出力低,负荷功率减少;在8∶00—15∶00时段,光伏功率增大,风光总出力大,负荷功率增加,相比于传统DR模型,反而增加了高峰负荷。
4.2 仿真结果及分析
构建考虑风光处理特性的微电网优化调度模型,在Matlab 2018环境下分别利用HNGO、NGO、CSA、PSO以及DE进行求解,最大迭代次数设置为2 000。所求得3种场景的日运行成本如表5所示,场景1下5种算法的迭代曲线如图6所示。
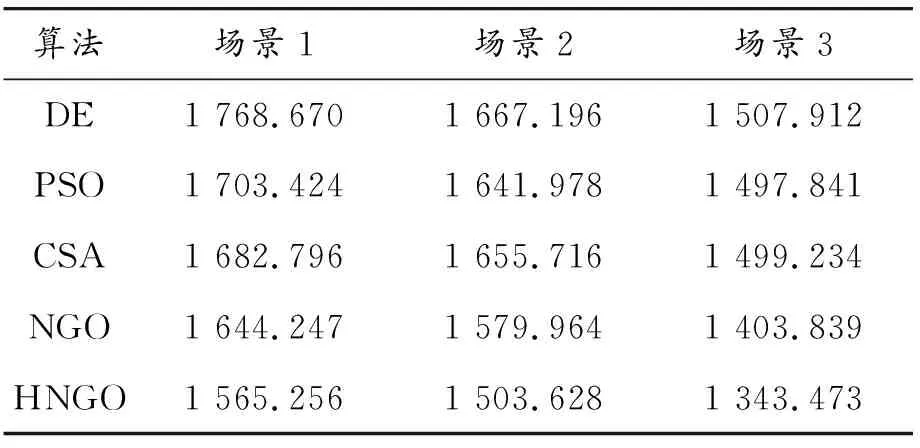
表5 3种场景求解结果 元
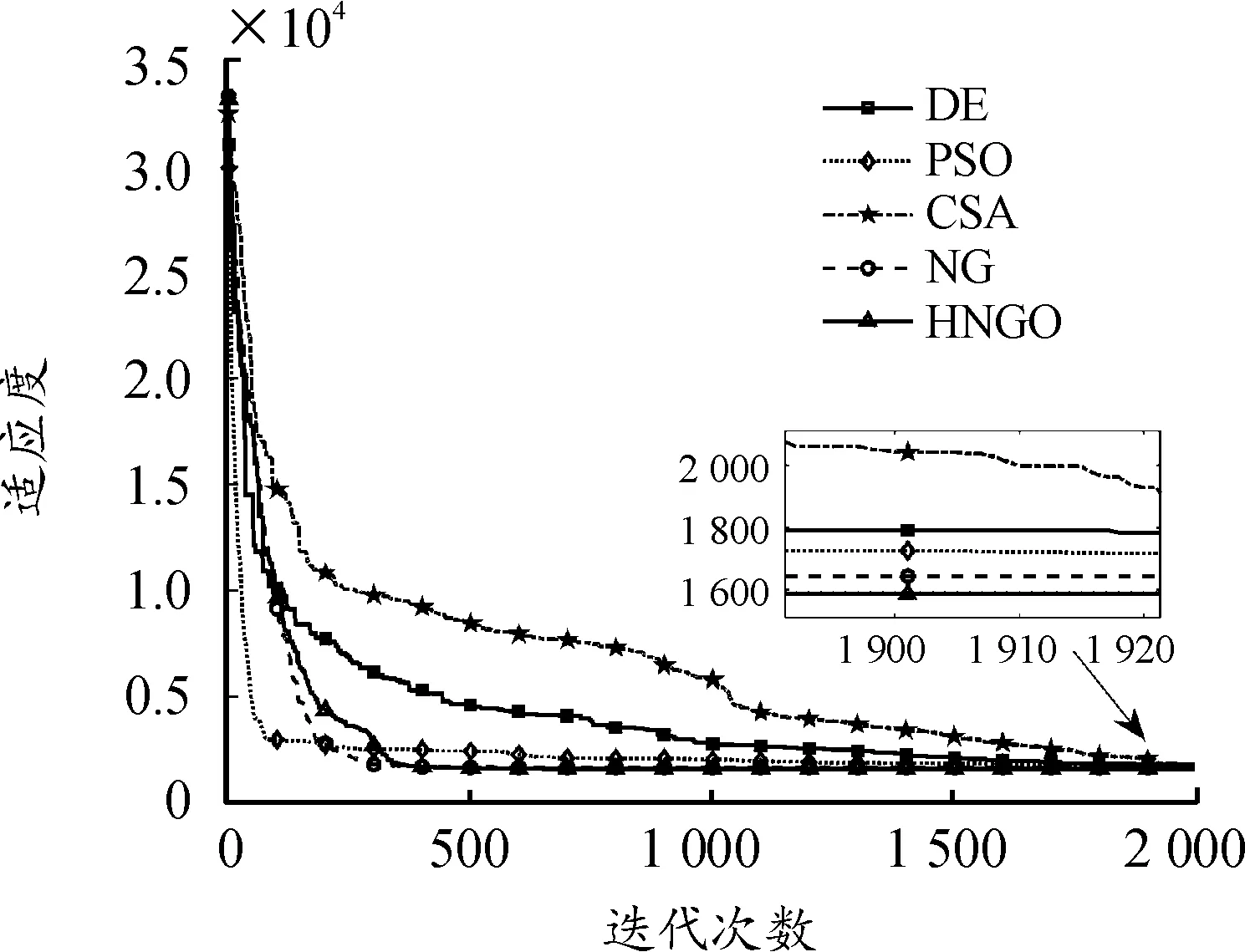
图6 场景1算法迭代曲线
由表5可知,HNGO在3种场景下的求解结果均为最好,场景1相比与其他4种算法成本分别减少了203.414、138.168、117.54、78.991元,证明在应对微电网优化问题时,HNGO具有更好的求解精度。
从图6可以看出,HNGO在求解过程中陷入了2次局部最优解,但都能跳出并找到更好的解,证明了改进策略的可行性;由于增加了算法的计算复杂度,HNGO的收敛速度略慢于NGO,NGO在第580次迭代时收敛于最小值,而HNGO在第630次收敛;PSO在第500次迭代时收敛到最小值,是5种算法中最快的,但求解精度不如HNGO。
各算法在场景2和场景3下相比场景1的日运行成本下降程度如表6所示。相比于场景1,场景2运行成本平均下降3.760%,场景3平均下降13.302%,表明相比于传统DR模型,所提DR模型对于降低微电网运行成本具有更好的效果。
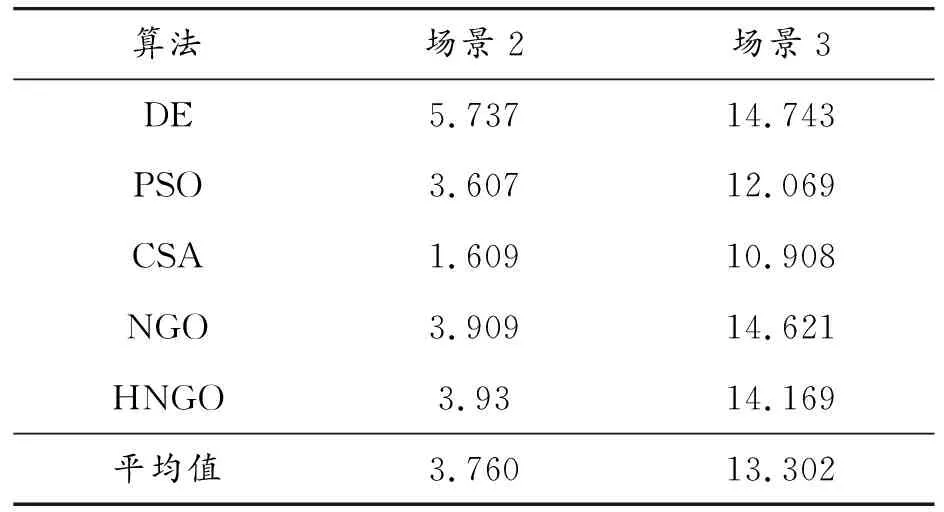
表6 相比于场景1运行成本减少程度 %
HNGO在3种场景下,求解得到的燃料成本如表7所示。相比于场景1,场景2、场景3燃料成本分别减少了4.016%和8.370%,场景3燃料成本减少幅度接近场景2的2倍,因此根据可再生能源出力特性来制定需求响应策略,能够使负荷曲线与可再生能源曲线具有更好的同步性,使可再生能源在出力高峰时段被充分利用,减少其他机组的出力,达到减少化石燃料消耗的目的。

表7 燃料成本
场景3下HNGO所求得的交互功率和蓄电池功率如图7所示。

图7 场景3交互功率和蓄电池功率
从图7可以看出,在0∶00~12∶00时段,交互功率小于0,一直处于售电状态;在13∶00~15∶00和19∶00~23∶00的负荷高峰时段,负荷功率增大,同时风光出力减小,此时向主网购电,且交互功率接近峰值。在此交互模式下,能够减少燃料的使用量,同时创造更多的收益,使电网实现清洁、高效运行的目标。
5 结论
以微电网为研究对象,建立了考虑可再生能源出力特性的需求响应模型。同时为了改善优化算法的求解精度,提出了一种多策略改进的北方苍鹰算法,并将其应用到微电网优化调度问题中。研究结果表明:基于风光出力特性制定电价,可以有效引导用户用电习惯向可再生能源出力靠近,使可再生能源得到充分利用,带来更好的经济效益;HNGO相比于NGO、CSA、PSO、DE具有更好的全局搜索能力和跳出局部最优解的能力。研究也有一些局限性,并未考虑对主网稳定性的影响。在仿真过程一直假设主网的功率是充足的,然而在高峰时段负荷增加的同时主网供电不足,微电网系统会出现功率失衡的情况,其波动可能会对主网稳定性产生影响。
