非机动车影响下考虑不均衡车流的信号控制方案优化方法

张广俊,张智勇,李永行,伍 权,乔 好

(1.北京工业大学 北京市交通工程重点实验室, 北京 100124;2.昆明理工大学 交通工程学院, 昆明 650500)

0 引言

非机动车出行需求的增加为信号控制优化问题带来新的挑战,信号相位设计是信号控制方案优化的核心,合理的相位方案可以极大提高交叉口的时空资源利用率[1]。机非交通流特性与非机动车过街模式作为影响相位优化设计的重要因素,但由于在实践应用中并未得到综合考虑,故往往会出现相位方案与流量结构不匹配、机非之间冲突严重的现象,进而导致交叉口通行秩序混乱,产生安全隐患,造成通行效率的降低[1-2]。如何根据交叉口车流特性和非机动车过街需求选择恰当的相位放行方案,并给出与之匹配的信号配时成为亟待解决的问题。因此,研究非机动车影响下不均衡车流的信号控制方案优化具有重要的实践意义。

国内外学者在相位优化设计、信号配时优化、非机动车过街模式的选择方面进行了大量研究。在交叉口相位优化设计方面,主要分为基于相位数的设计方法、基于车流的设计方法2种模式[3]。前者以相位数最少为目标来减少相位间切换[4-6]。尹丽子利用数学规划中“圆染色体”的思想求解交叉口的最优相位数[7- 8],但并不适用于搭接相位的设计。后者主要给予各流向流量相近的车流同一信号灯显示,以此来最大程度地利用绿灯时间,但需要结合信号配时参数进行协同优化。聂磊等[9]采用集合论与最优化的方法建立两阶段相位生成模型;Babicheva[10]将排队论的思想引入信号相位设计,得到了交叉口延误最小化的显示解,但未考虑非机动车过街行为的影响。李娟等[11]考虑非机动车过街模式的差异,提出了基于人均延误最小的信号配时优化模型,但未考虑不同机动车放行相位之间的差异性。林晓辉[12]以案例交叉口为例,对比了高峰、平峰和低峰时采用对称放行和轮转放行方案的各项评价指标。张小宁等[13]介绍了轮转放行的优点,从定性的角度给出了适应条件,仿真分析发现相同条件下轮转放行方案优于对称放行方案。王进等[14]以合流放行、对称放行和轮转放行三种基本机动车放行相位为基础,提出了三者相互衔接的搭接相位设计方法,可有效解决各流向间饱和度差异大的问题。张亮等[15]为克服不对称交通流采用对称放行的局限性,确定了不同交通场景下机动车对称放行与轮转放行的不对称系数临界值,给出2种设计方案的适用范围,但研究中将进口道作为一个整体,并未考虑直行与左转交通流的不均衡性。为此,蒋贤才等[16]根据对向交通流间的差异,提出了一种机动车动态相位方案生成规则,但该方法缺乏对非机动车不同过街模式的考虑。马新露等[17]基于元胞传输模型提出了一种四路环形交叉口多进口协同的放行方法,大大降低了交叉口延误。在信号配时优化方面,相关学者大都以机动车为研究对象,选取交叉口总延误[18]、车均延误[19]、停车次数[20]、排队长度[21]、尾气排放[22]中的一个或多个参数为目标进行优化,并采用遗传算法、蚁群算法等智能优化算法进行求解[21,23,24]。其中,蚁群算法具备较高的精度与稳定性,但寻优过程存在易陷入局部最优的问题。另外,研究中缺乏对非机动车及不同交通参与者之间载客数差异的考虑。

在非机动车过街模式适用条件方面,现有研究大都以两相位交叉口为研究对象进行分析。王嘉文等[25]对两相位交叉口时间分离放行法的设置效果进行评价,确定了慢行交通专用相位的设置阈值。顾晨阳[26]研究了两相位交叉口条件下空间分离法和时空分离法的交通量适用条件,给出了非机动车过街模式选择的阈值。Grigoropoulos等[27]分析了非机动车交通量与交叉口通行能力的关系,指出左转非机动车会对机动车通行造成较大的延误,恰当的放行方案能有效降低机非间的冲突频次。阮守继[28]分析了信号交叉口非机动车的交通特性,并对两相位制、多相位制、错时绿灯法和绿色箭头灯指挥法四种非机动车放行方法进行了详细介绍,通过采取合适的放行方法来减少机非之间的干扰。

综上,相位优化设计过于依赖实践经验,缺乏对搭接相位的考虑,各相位放行方案的定量适用范围不够明确,鲜有学者综合考虑机非交通流特性和非机动车过街模式对相位优化设计的影响,且后续信号配时优化中对不同交通参与者载客数的差异性考虑不足。为此,以对称放行+二次过街、对称放行+一次过街、轮转放行+二次过街、对称搭接放行+一次过街/二次过街共5类放行方案为研究对象,考虑非机动车的膨胀特性对机动车延误的影响,基于机动车交通流方向不均衡性提出一种信号交叉口动态放行方案,并建立延误估计模型来表征不同放行方案之间的延误差异,通过数值分析确定不同放行方案的定量设置条件,进一步以人均延误最小为目标,采用改进蚁群算法求解出对应放行方案下的最佳信号配时方案。

1 信号交叉口放行方案设计

信号交叉口放行方案选择本质是寻求机动车相位方案和非机动车过街模式最优组合的过程。机动车流的不均衡性是影响放行相位选择的关键因素,而非机动车的膨胀特性则会对机动车流产生不同程度的影响,同时影响其自身的放行模式。

1.1 机动车流方向不均衡性

常见的机动车放行相位有对称放行、轮转放行、混合放行、合流放行和搭接相位放行[14]。交通流时空分布的不均匀性决定了采用何种机动车放行相位。考虑同一相位不同方向间的流量差异,引入相位交通流不均衡系数的概念[16],将其定义为某相位内对向交通量间的流量差与两者中最大交通量的百分比,通过比较aj与临界值aj0的大小来判别交通流的均衡状态,进而确定机动车放行相位。该系数计算式为:

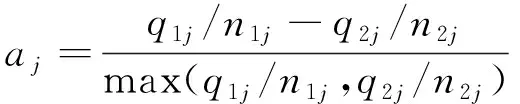
(1)

式中:aj为第j相位的交通流不均衡系数,j∈[1,4],分别对应东西左转、直行和南北左转、直行,用s1、s2、s3、s4来表示4个方向的饱和流率;q1j为第j相位第1车道组到达交通量;q2j为第j相位第2车道组到达交通量;n1j为第j相位第1车道组对应的车道数;n2j为第j相位第2车道组对应的车道数。

1.2 非机动车膨胀特性

非机动车过街模式与机动车通行效率之间的关系密切。具体体现在:

1) 机非同行时左转非机动车一次过街,非机动车的扩散效应使其在交叉口内部的膨胀宽度迅速扩大,这种横向干扰行为迫使左转机动车减速来避免冲突,严重影响机动车的运行效率;

2) 人非同行时极大降低了左转非机动车对机动车通行的影响,但直行与左转非机动车同时放行使得直行的非机动车流大幅度上升,这种“流量叠加”现象也会增加待行区的空间压力,对相邻机动车道的运行产生较干扰,同时很大程度上牺牲非机动车的效率。

随着非机动车在绿灯相位时的释放,分布于交叉口内部的非机动车群始终处于动态变化中。为直观反映非机动车不同过街方式释放过程中对机动车的影响,以典型双向六车道交叉口为例,将交叉口内部区域划分成若干等大的网格,采用George软件对非机动车通过交叉口的数量、时刻位置、坐标进行提取(共计1 018个样本),并记录非机动车通过每个位置的频率,将其绘制成热力图来体现非机动车的分布特性。如图1所示,可以清晰地看到,非机动车通行过程中会对机动车造成较大影响。

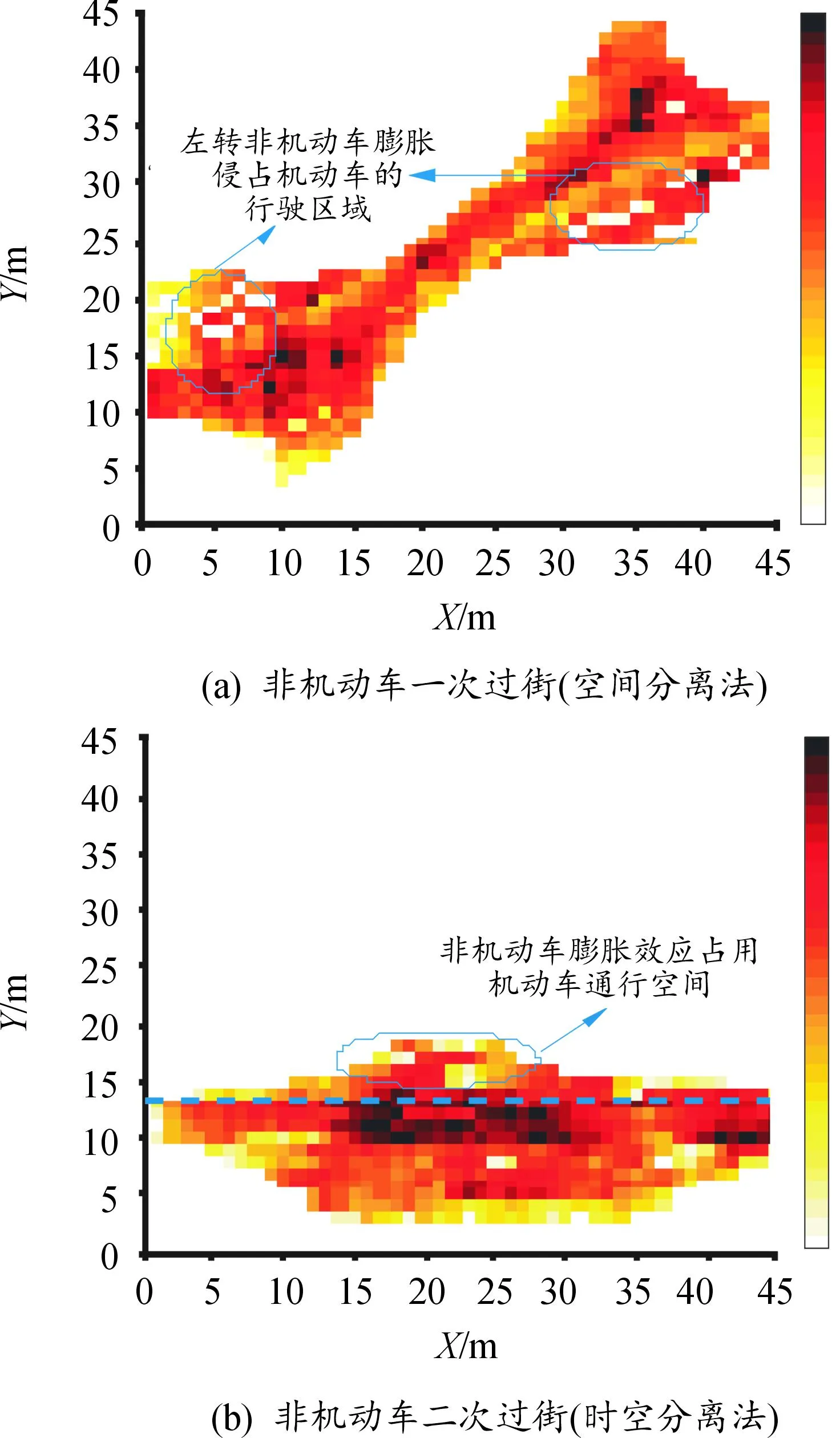
图1 非机动车通过交叉口分布热力图

机非之间的干扰主要体现在非机动车流的膨胀特性导致其占用相邻机动车的通行空间,进而造成交叉口延误。由图2可知,非机动车放行过程中的膨胀宽度很大程度影响了机动车通过交叉口的时间。

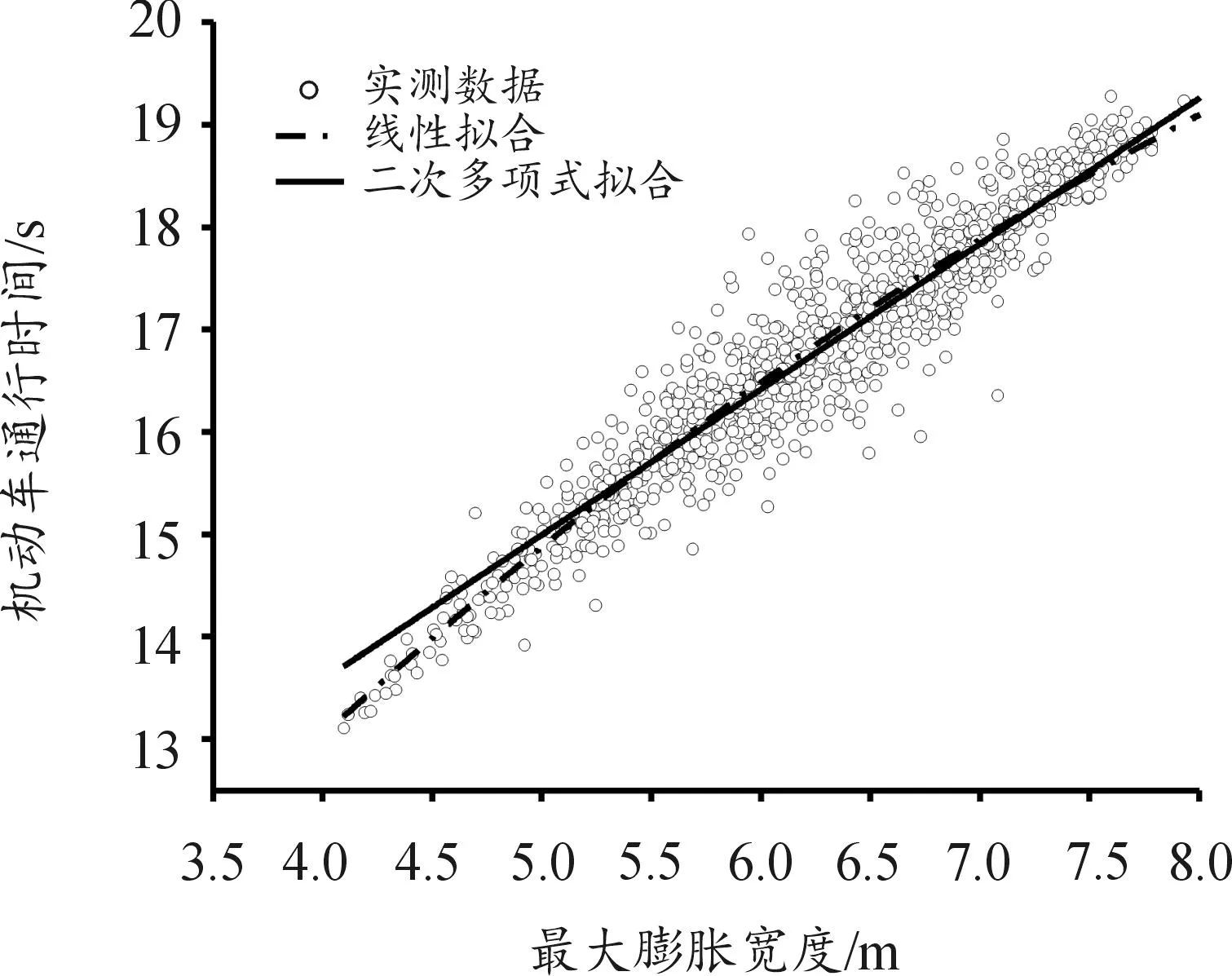
图2 机动车过街时间与非机动车膨胀宽度拟合曲线

通过实测数据对机动车通行时间与非机动车膨胀宽度之间的关系进行线性和非线性回归拟合,发现非线性回归的拟合度更高 (R2=0.874),且P<0.01,表示模型具有统计学意义,则回归模型可由式(2)表示为:

Tm=-0.110W2+2.893W+3.160

(2)

式中:Tm为受非机动车影响的机动车的通行时间;W为非机动车过街时的膨胀宽度。

为进一步量化非机动车放行过程中对机动车的影响,引入“影响强度”的概念,由有无非机动车影响时机动车的通行时间来表示,如式(3)所示,用来反映机非之间的相互作用。

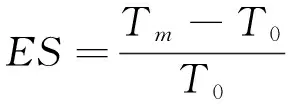
(3)

式中:T0为不受非机动车影响的机动车通行时间。

利用非机动车影响强度(通行时间比值化的形式),可将不同放行方式下非机动车对机动车的延误进行归一化处理,即机动车延误随着影响强度的增大而升高。如图3所示,通过实测数据发现影响强度与机非流量之间成正比关系,印证了该指标的合理性,故将其纳入机动车延误估计模型中。

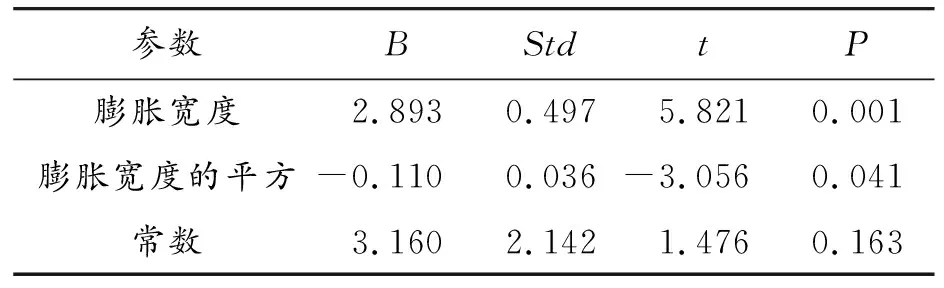
表1 机动车通行时间与膨胀宽度回归模型结果

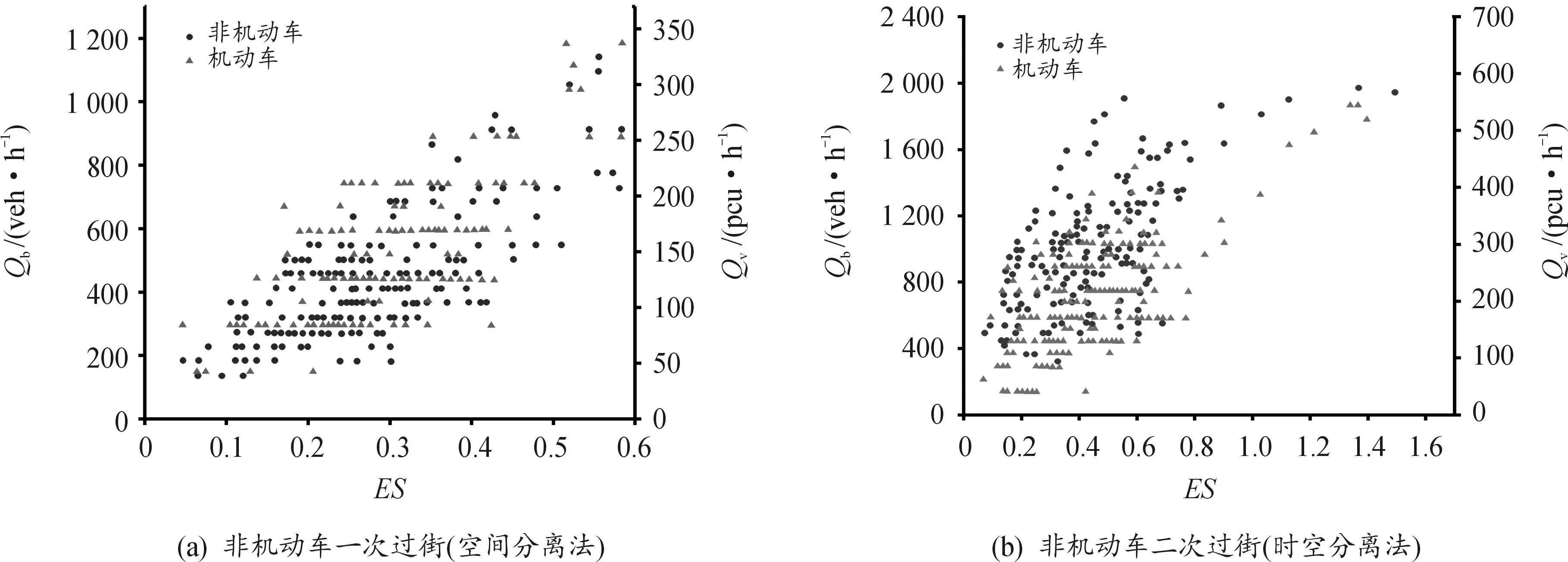
图3 影响强度与机非流量关系

1.3 信号交叉口动态放行方案设计

由式(1)可知,根据各个方向直行和左转不均衡系数的差异,可以将放行方案分为5种情形,并以平衡各车道间饱和度、合理利用绿灯时间为原则,给出每种情况下的最佳放行方案,如表2所示。

表2 基于相位交通流不均衡的放行方案设计

2 考虑不同放行方案的延误估计模型

2.1 假设条件

1) 不考虑各方向右转车流和行人交通对信号交叉口放行方案选择的影响。

2) 信号交叉口各进口道机动车左转车流量需求较大(设置左转保护型相位),每个周期内无非机动车滞留。

3) 机动车采用轮转放行时,考虑到左转非机动车与直行机动车冲突严重,故非机动车默认采取时空分离法进行二次过街。

2.2 机动车延误

参考美国HCM2016中的延误模型,将机动车延误划分为不同车道组,主要分均匀延误udij、增量延误idij和冲突延误三部分进行计算。冲突延误主要体现在2个方面:非机动车与右转车辆之间的冲突、非机动车的膨胀效应对机动车产生的横向干扰冲突。无论采用何种放行方案,非机动车与右转车辆之间的冲突都不可避免,故不予考虑。而膨胀冲突与非机动车占比、膨胀宽度、交叉口饱和度等诸多因素有关[29],本质还是伴随相位更替产生,故将其作为非机动车干扰系数udij对信号延误进行修正。其中,udij与idij的计算如式(4)和式(5)所示。

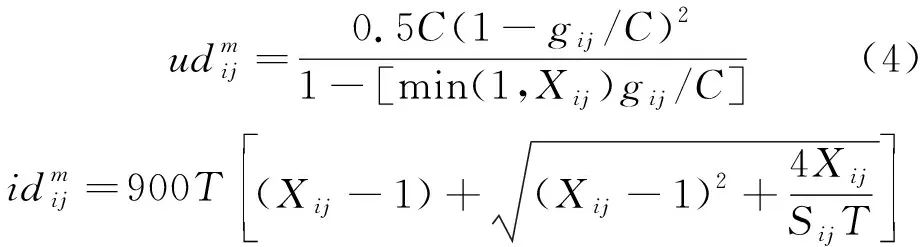
(5)

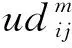
如图4所示,三角形OAB表示交叉口采用传统相位方案时产生的延误。特别地,当采用搭接相位延长绿灯时间Δt1s的放行方案时,因南北左转小流量方向绿灯时间早断会造成延误增加,可用梯形OBEG的面积来计算,如式(6)所示;相应地,直行相位的提前开启会减少Δt1s时间内释放车辆的延误,可用梯形ABFD的面积来计算,如式(7)所示。i的取值根据式(6)中q11与q21的大小决定,若前者大于后者,i值取1,反之取2。

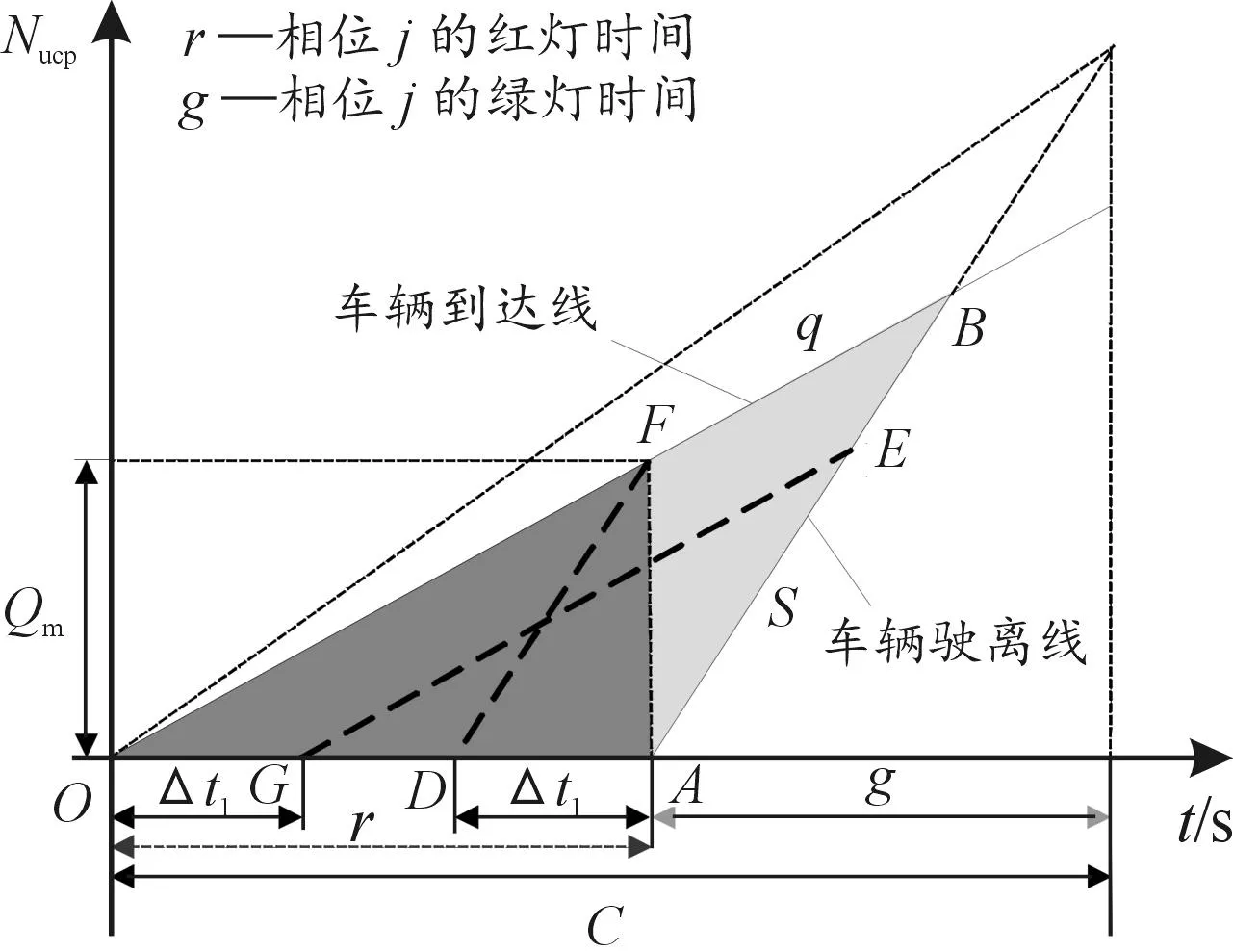
图4 设置搭接相位带来的交叉口延误变化量

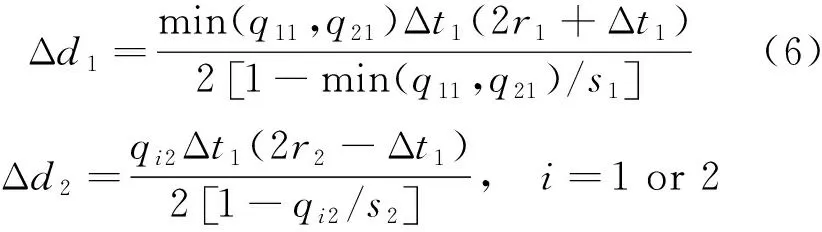
(7)

南北方向的延误变化量ΔD可由直行相位早启带来的延误减少量与左转相位小流量方向早断引起的延误增加量之间的差值来表示,如式(8)所示。

ΔD=Δd2-Δd1

(8)

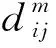
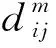
利用经验模型来确定非机动车干扰系数γ与其影响因素之间的关系,研究其对机动车延误造成的影响。经过回归分析得到各个变量之间的函数关系如式(10)所示。

γ=0.352Pe+0.011S+0.402ES+1.086

(10)

因此,1个周期内机动车的总延误可由式(11)求得。

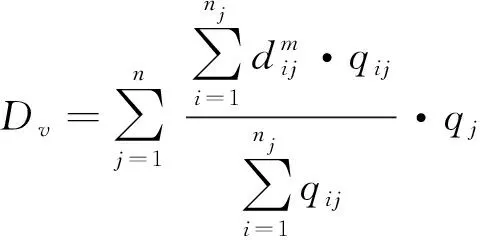
(11)

式中:nj表示相位j的车道组数;qij表示相位j车道组i的机动车交通量;n为信号周期相位数量;qj表示相位j的机动车交通量。

2.3 非机动车延误

非机动车放行方法主要有3种:时间分离法、空间分离法和时空分离法。时间分离法是专设一个非机动车和行人专用相位,不少学者在慢行交通专用相位方面的研究结果表明[26,30],时间分离法在道路等级较低的次干路和支路具备较好的实施效果,但在主干路交叉口的效果欠佳,故将其作为所有放行方案中的严格劣策略,着重对空间分离法和时空分离法下的非机动车延误进行分析。

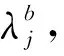
时空分离法保证机动车的优先通行权,让左转非机动车进行二次过街来减少对机动车的干扰。以南进口为例,当非机动车进入交叉口遇到绿灯时,以速度vb直接到达对面候驶区(假设过街距离为LAC,见图5),待东进口直行相位变为绿灯时完成二次过街。此类情况下,非机动车在1个周期内产生的控制延误表示为[19]:

图5 不同非机动车过街方式示意图

(13)

当非机动车进入交叉口遇到红灯时,该过程的延误求解方法与空间分离法相同,待南进口的直行相位变为绿灯时,非机动车便可到达对面候驶区进行等待,直到东进口直行相位变为绿灯时可完成二次过街。则1个周期内非机动车的控制延误表示为:

与空间分离法不同的是,二次过街模式下非机动车会连续经历2次信号灯,非机动车不仅会产生控制延误,还有因绕行造成的延误。由图5可知,1个周期内非机动车绕行延误可由式(15)求得。

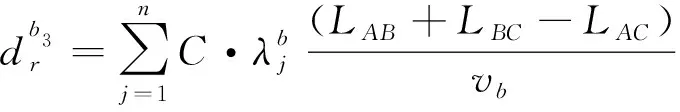
(15)

式中:LAB表示进口道非机动车等待区A与二次过街候驶区B之间的距离;LBC表示候驶区B与出口人行横道的外边缘线C之间的距离。

根据上述分析,在交叉口采取时空分离放行法的情况下,非机动车产生的总延误表示为:

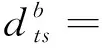
(16)

综合上述2种非机动车放行方法,则1个周期内机动车的总延误可由式(17)求得。

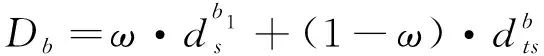
(17)

式中:ω的取值为0或1,ω取1时表示非机动车采用空间分离法,反之为时空分离法。

2.4 基于改进蚁群算法的最优信号配时方案

2.4.1目标函数

人均延误能够较好地反映多个交通主体参与下交叉口的运行状态。综合考虑机动车和非机动车的效益,以两者的人均延误最小为目标[11],以信号周期时长、有效绿灯时间以及交叉口饱和度为约束条件,确定不同放行方案下的最优信号配时方案,模型的目标函数可表示为:

(18)

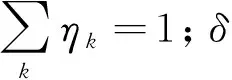
2.4.2 求解算法

蚁群算法(ant colony optimization,ACO)是一种随机优化算法,可通过多维搜索求得问题的最优解。研究表明,该算法具有很多优良特性,已在诸多组合优化问题中取得了好的效果。它的基本原理是利用蚂蚁间的种群协作行为来寻得最优路径,每只蚂蚁在觅食过程中都会释放一种叫信息素的化学物质,通过相互之间的通信协作,越来越多的蚂蚁便会自发聚集到信息素最强的路径,从而达到自动寻优的目的[31]。

借鉴罚函数法处理的思想,把约束条件当作惩罚因子,将其转化为无约束的优化问题。假设每只蚂蚁的评价函数为Ui,则能见度ΔUij可表示为:

ΔUij=Ui-Uj, ∀i,j

(19)

其次,蚂蚁会按照某一选择概率转移到下一节点,将其定义为:

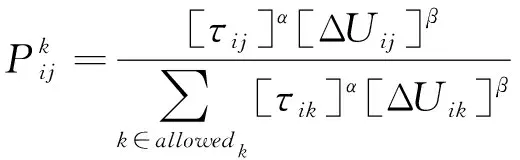
(20)

式中:τij为第k只蚂蚁从i到j的信息素浓度;α、β是2个常数,分别为启发因子和期望因子;allowedk为蚂蚁k接下来被访问的节点集合。

由于正反馈的特点会导致扩大初始环境中不同位置的信息素浓度,故而整个系统会快速收敛于“最优”路径。倘若该路径为次优解,那么整个过程便会陷入局部最优而无法逆转。为克服该缺点,从信息素更新的角度着手,通过信息素平滑机制来提升算法全局寻优能力。倘若连续多次迭代的最优解都相同,则借助式(21)对信息素进行平滑:

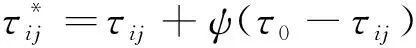
(21)

改进后蚁群算法求解的主要步骤如图6所示。根据设定规则达到最大迭代次数,最终得到延误最小的不同放行方案下对应的最佳配时参数。需要注意的是,对交叉口设定不同放行方案进行计算时,应根据各自的情况重新输入目标函数,改变参数设定和约束条件的限制。

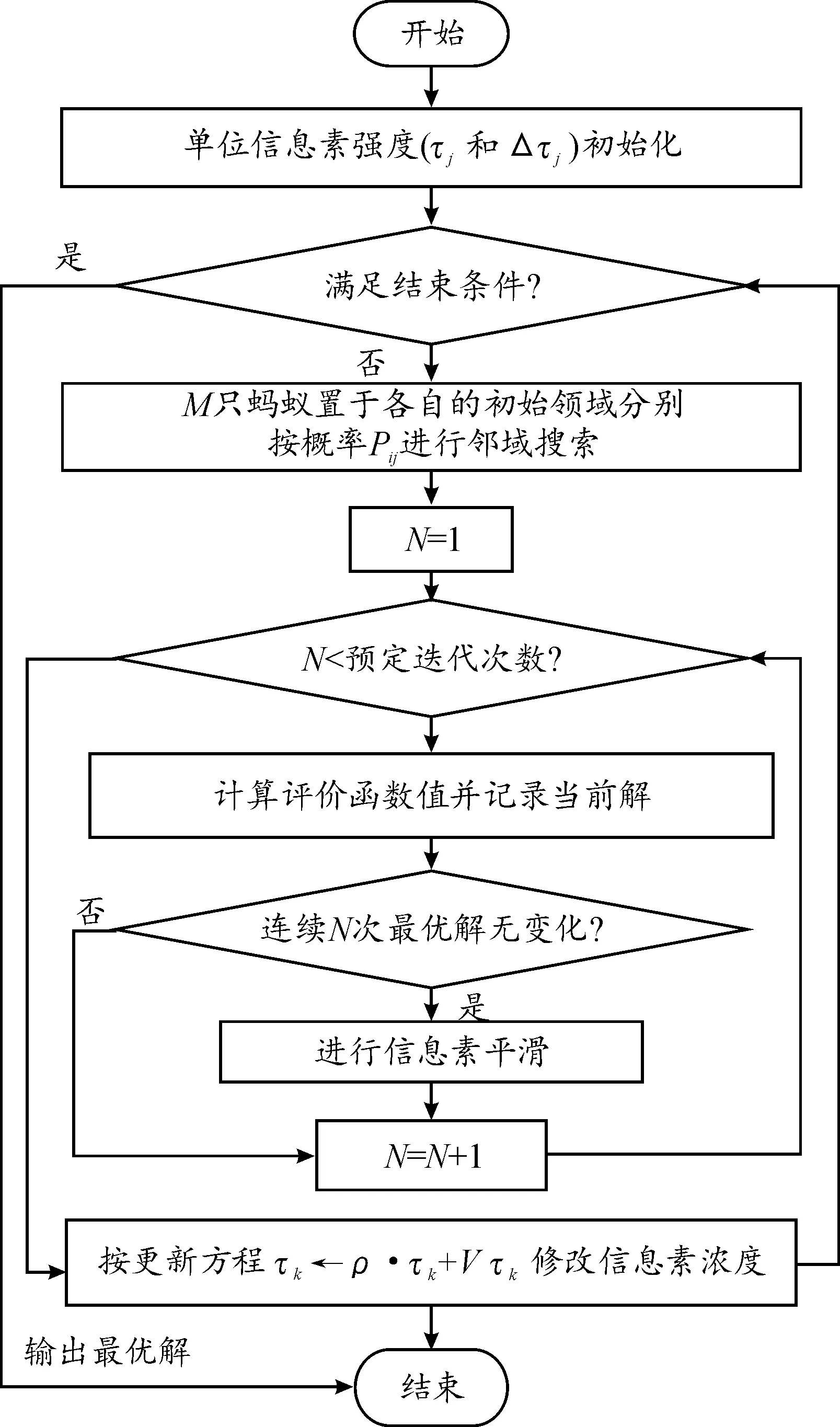
图6 蚁群算法迭代求解流程

3 仿真分析与实例验证

3.1 灵敏度分析

为探究所建立模型中交叉口采用不同放行方案时,各参数变化和延误的关系,运用Matlab软件对模型进行数值仿真与灵敏度分析。以典型双向六车道交叉口的南北进口为例,在低流量(0～800 pcu/h)的条件下,不均衡系数和非机动车左转交通量的变化并不会对交叉口延误产生显著影响,此时采用对称放行+一次过街效果较好。假设南、北进口(直行和左转)的交通量为中高流量(800 ～2 000 pcu/h),左转流量和同直流量和之比分别为1∶2、1∶3、1∶4时,通过改变机动车左转不均衡系数和非机动车左转流量来分析和交叉口延误的关系。最终得到交叉口分别采用对称放行+一次过街、对称放行+二次过街、轮转放行+二次过街时,不同交通量条件下南北方向的人均延误仿真结果,如图7所示。

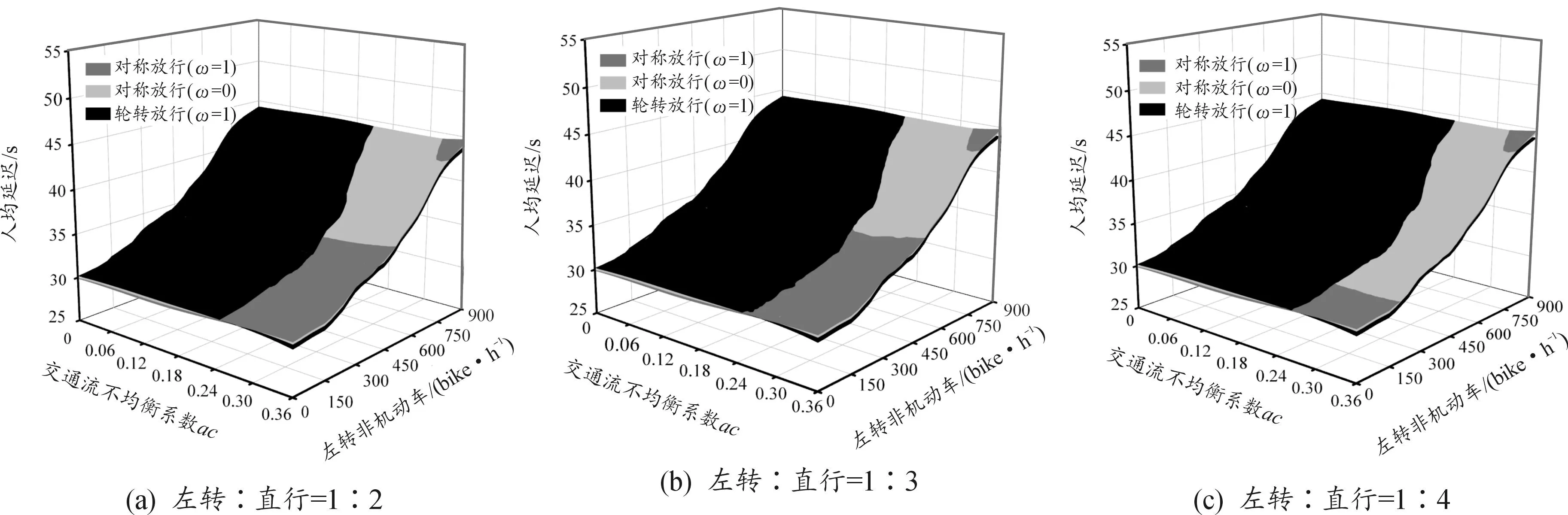
图7 不同放行方案的延误仿真结果

从图7中可以得出以下结论:

1) 在中高流量条件下,不均衡系数对于不同机动车放行相位设置的影响比较明显。当不均衡系数大于0.25时,轮转放行产生的延误更小,对称放行与轮转放行之间的延误差值随着不均衡系数的增大而增大;当不均衡系数小于0.25时,对称放行产生的延误要小于轮转放行。

2) 对非机动车放行方法而言,当不均衡系数小于0.25、左转和直行流量之比大于1∶3、非机动车左转流量大于100 bike/h时,空间分离法产生的延误要比时空分离法小,且二者之间的延误差值随流量增大而变大,这是因为一次过街时非机动车的控制与绕行延误均较小,但当其增大到500 bike/h时,左转弯非机动车的膨胀效应导致机非之间的冲突严重,进而造成交叉口通行效率下降,此时采用空间分离法更具优势;当流量比小于1∶3时,左转机动车较少,时空分离法下左转相位的绿灯时间可以根据左转需求进行适当调整,而空间分离法下由于左转非机动车过街的绿灯时间约束,不能缩短左转相位的绿灯时间而导致机动车的延误增加,因此空间分离法产生的延误要大于时空分离法。需要注意的是,左转非机动车的流量也有一定的约束上限值。当流量叠加和非机动车候驶区溢出现象较为严重时,时空分离法也不能起到减少机非干扰的效果,此时需要设置慢行交通专用相位或采用非机动车绿灯提前启亮的方法。

为求得机动车交通流的不均衡系数阈值,保持东西进口方向的交通量以及非机动车流量不变,固定南北左转交通量及不均衡系数为0.25。与此同时,在南北直行交通量之和不变的前提下,改变不均衡系数的大小,从而得到不同临界值条件下的南北直行车辆的延误变化,如图8所示。

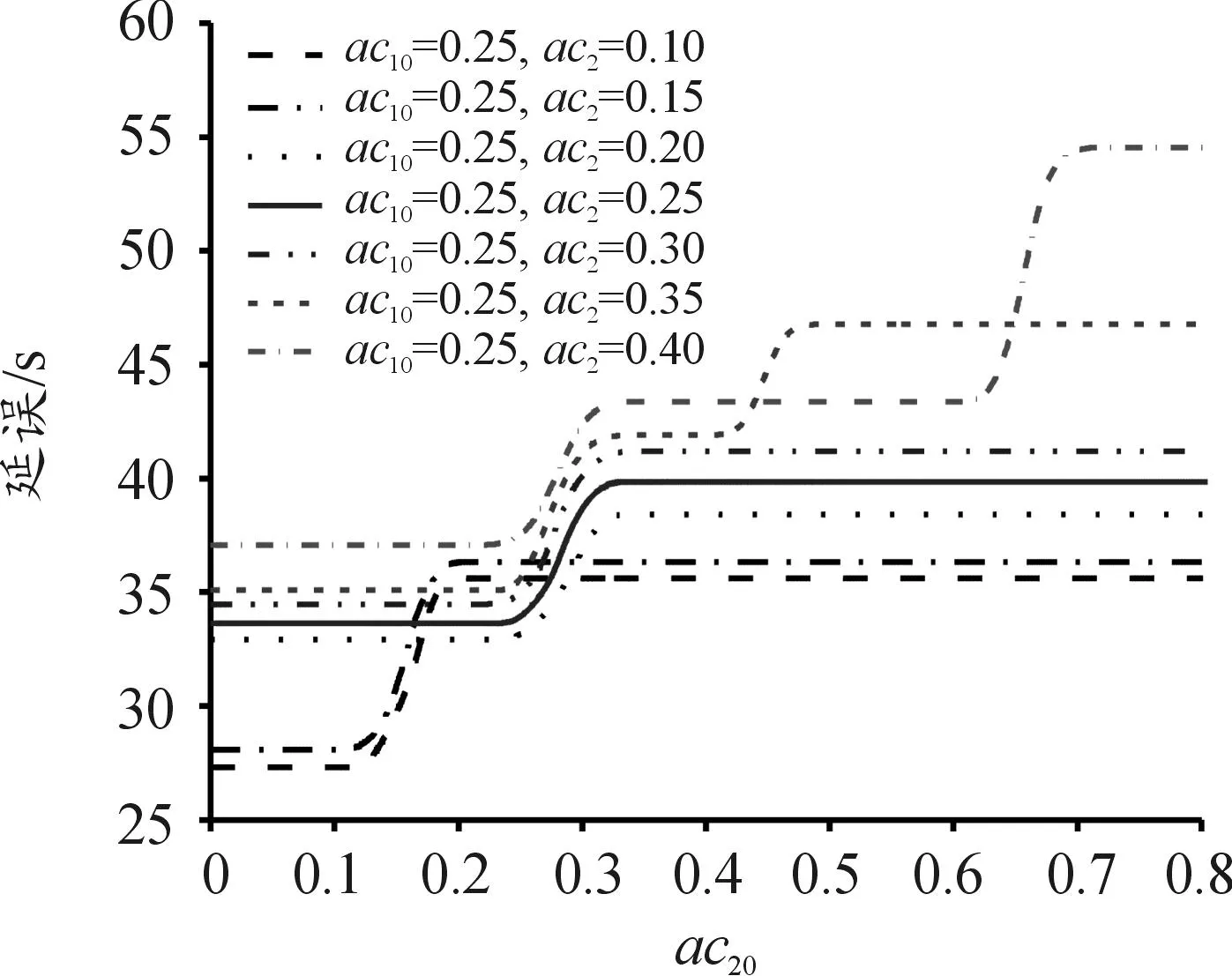
图8 不均衡系数阈值与人均延误的关系曲线

由图8可知,在不同直行不均衡系数的取值下,交叉口延误随阈值的变大呈现增长态势,当ac20大于0.25时延误急速增长。因此,考虑将0.25作为直行不均衡系数的临界值。原因如下:因交通流不均衡系数可用来判别交叉口采用何种放行方式,故该阈值的选取要合理且满足尽可能多的交通流场景。当取值较小时,交通流出现微小波动便会判定交叉口采用轮转放行的方案;当取值较大时,即使交通流不均衡系数变得很大,仍会判定交叉口采用对称放行的方案。根据木桶效应,满足关键车流的需求势必会造成小流量方向绿灯时间无法充分利用,同时交通流量比增大也会使得信号周期变长,进而造成交叉口延误的增加,此时再通过信号配时优化往往也达不到理想效果。同样地,可考虑用相同原理来获得其他方向的不均衡系数阈值。

3.2 数据调查及参数设置

选取北京市典型主干路交叉口作为案例进行研究。该交叉口早晚高峰期间交通量较大,调查地点平面图见图9。

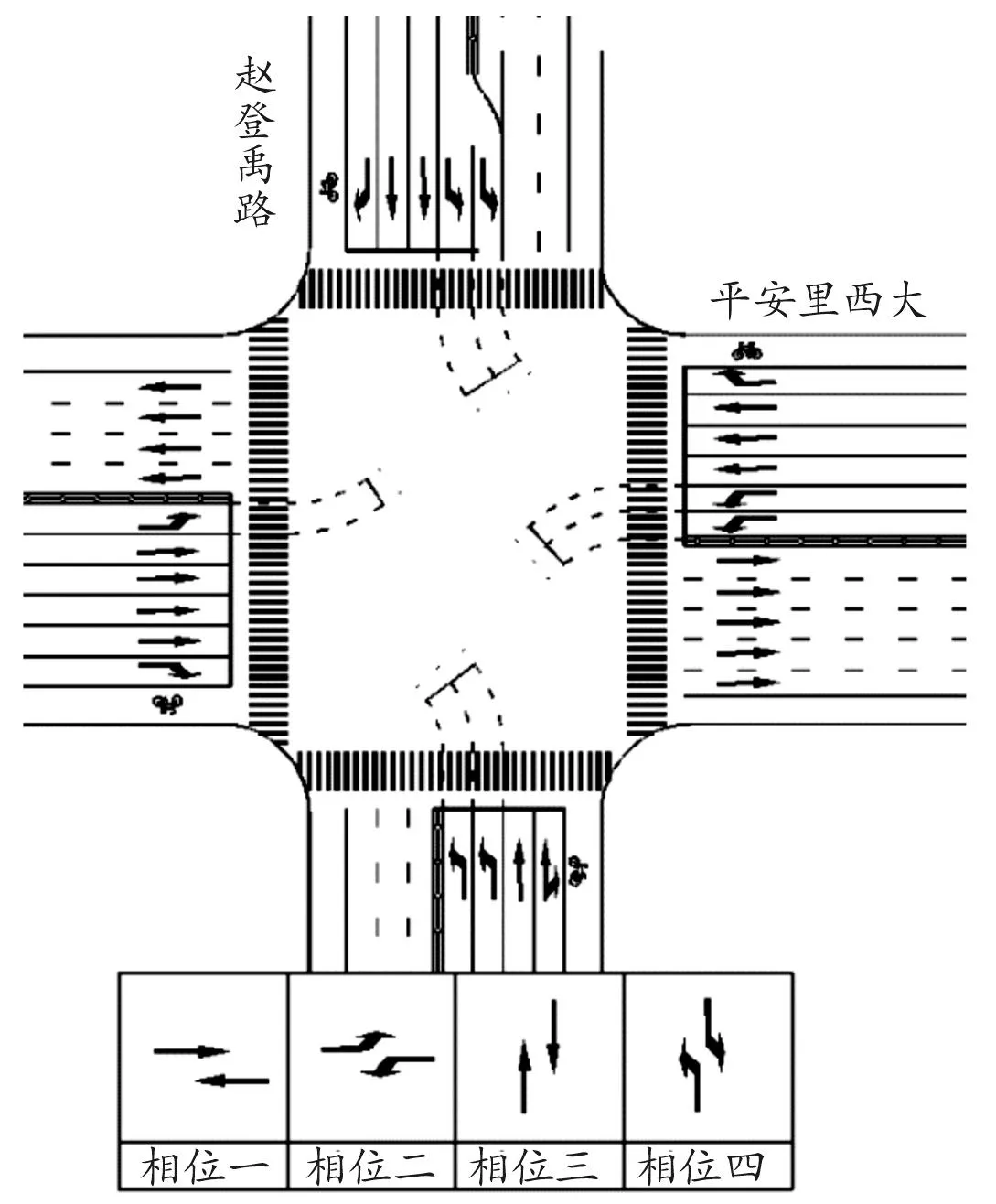
图9 调查地点平面图

机动车以小轿车和公交车为主,平均载客数分别按2.3、15.2计算,非机动车以自行车和电动车为主,平均载客数按1.1计算。根据现场调查得到的早高峰(7∶30—8∶30)流量和信号配时方案如表3所示,计算机动车交通量时均换算为标准车型。

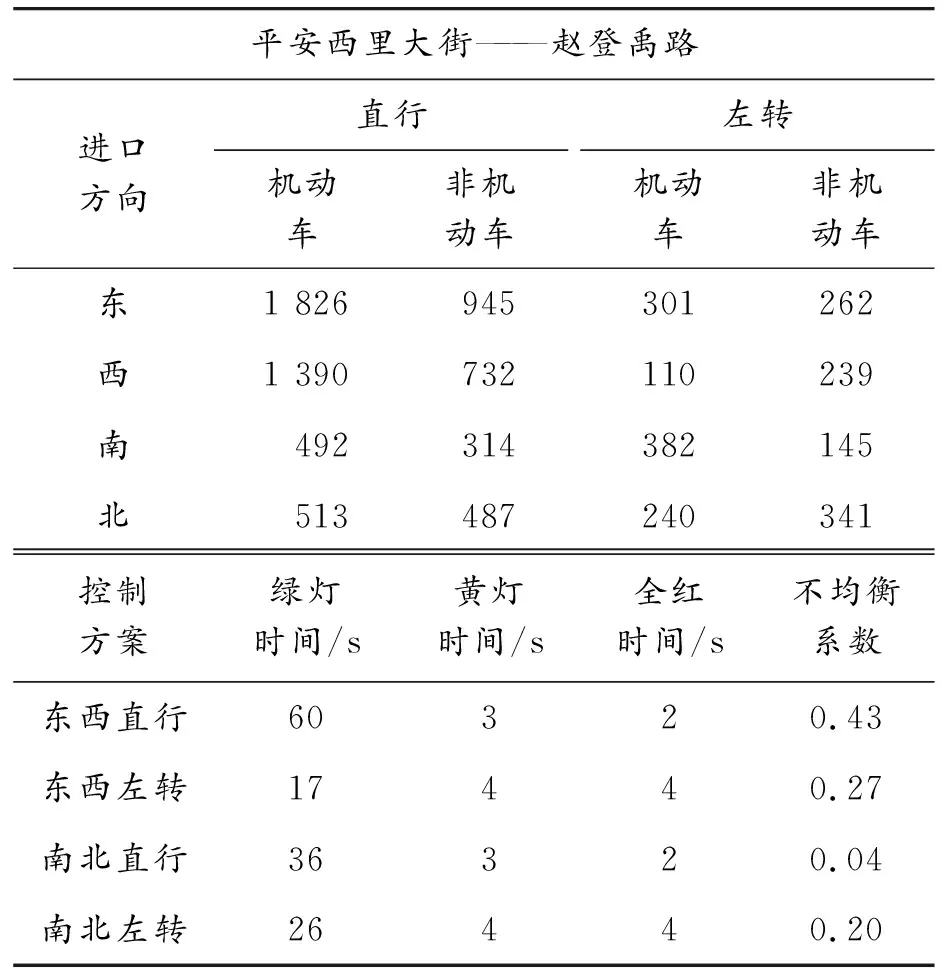
表3 早高峰时段流量(pcu/h)及信号配时方案

改进蚁群算法参数设置:蚂蚁数量为50,α=0.3,β=2,最大迭代次数设为200,信息维持率ρ=0.7,局部搜索步长取为0.1,信息素初始量τ0=0.000 1。此外,设定直行和左转最短绿灯时间均能保证行人和左转非机动车安全通过交叉口,其中南北走向过街长度LAB为48 m,东西走向过街长度LBC为40 m,行人过街步速取1.2 m/s,非机动车速度取4.5 m/s,由此近似计算出每个相位的最短绿灯时间,如表4所示。

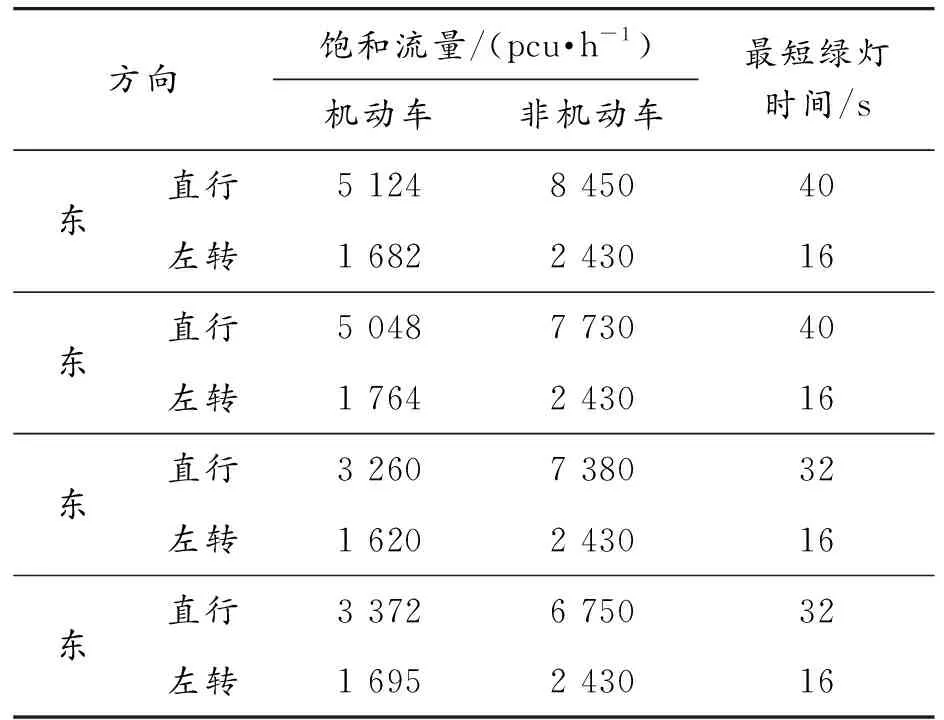
表4 模型关键参数统计

依据绿灯间隔时间和关键流量比可确定最小、最大信号周期分别为Cmin=120 s和Cmax=180 s;交叉口饱和度过大或过小都难以通过改变放行方案来减小交叉口延误,经试算确定饱和度的范围为(0.75,0.93)。由调查数据可得,非机动车一次过街模式下各个方向的Pe取值分别为0.05、0.06、0.08、0.12,ES取值0.30,二次过街模式下Pe取值分别为0.12、0.12、0.18、0.23,ES取值0.25。根据表3中各个方向的不均衡系数可知,东西方向直行和左转同向不均衡,南北方向直行均衡而左转不均衡。根据1.3节,东西方向采用对称搭接放行方案,南北方向采用对称放行方案。

3.3 结果分析

利用Matlab R2020a软件对所建立模型进行仿真,采用改进蚁群算法对优化模型进行求解,将其转化为编程语言并对各参数进行赋值,最终得到交叉口在轮转放行和对称搭接放行下对应的信号配时参数。混合放行时的信号周期C=158 s,每个相位的绿灯显示时间分别为52 、30、34、22 s。对称搭接放行时的信号周期C=142 s,各个相位的绿灯显示时间分别为40 、13、18、34、22 s。2种方案的信号配时情况如图10所示。

图10 不同方案方法对应的信号配时图

将交叉口相关参数值及现状方案、混合放行方案和对称搭接放行方案的配时参数分别代入式(18)中,求得不同方案下的人均延误,结果如表5所示。

表5 不同放行方案实施效果

结果表明,现状方案的交叉口延误相对较大,当采用混合放行方案和对称搭接放行方案进行优化时,人均延误都有不同程度的降低。由于多股不均衡交通流协调放行,充分利用了交叉口现有时空资源,减少了各方向车辆排队长度及机非之间的相互干扰,使得人均延误大大降低。相比于现状方案,所提出的放行方案及信号配时使人均延误分别降低了25.81%和23.72%。当机动车采取对称搭接放行时,空间分离法(ω=0)比时空分离法(ω=1)的人均延误要低1.1 s。综上,交叉口采用对称搭接放行+非机动车一次过街的放行方案最佳。

4 结论

将非机动车膨胀效应作为对机动车运行的干扰因素,建立不同放行方案下的机非延误模型,从机动车交通流方向不均衡性角度提出一种交叉口放行方案,并以人均延误最小为优化目标求出各放行方案对应最佳信号配时。运用仿真分析得到传统放行相位的定量适用条件,并以实际交叉口为例,利用Matlab仿真程序进行验证。结果表明,相比于仅采用单一放行相位,所提出的放行方案使人均延误降低13.6 s,降幅为25.81%,信号周期时长缩短13.94%,说明该方案能有效提高交叉口的运行效率。研究成果可为不同交通需求下的放行方案选择提供参考。

由于目前仅针对机动车和非机动车不同放行方法下的延误情况进行分析,故下一步将在此基础上考虑行人因素,从安全和效率2个方面对多交通参与者进行综合评估。另外,本研究聚焦于主干路交叉口常用的相位控制方案,未将两相位合放条件下的控制方案考虑在内,这些都是后续研究重点考虑的问题。