数据降维与K-均值聚类的质量评估
2024-02-05何选森刘润宗樊跃平熊茂华
何 帆,何选森,刘润宗,樊跃平,熊茂华
(1.北京理工大学 管理与经济学院, 北京 100081;2.广州商学院 信息技术与工程学院, 广州 511363;3.湖南大学 信息科学与工程学院, 长沙 410082)
0 引言
在大数据时代,对数据的分析和处理变得越来越重要,而对数据的分类则在数据分析中占据至关重要的地位,分类又包括监督和无监督2种。监督分类[1]是指对具有类标签的样本数据进行训练与学习,通过判别函数和判别准则进行分类。无监督分类[2](或称聚类[3])是用于处理无分类标签的数据,属于探索性数据分析[4],由于它可以发现数据固有的结构,因而获得了广泛的应用。聚类分析具有划分聚类、层次聚类和单个(individual)集群3种常见的聚类结构,其中划分聚类应用最为广泛,例如K-均值类型的算法[5]。由于此类算法易于执行且计算效率高而获得了广泛的应用,从而成为经典的聚类算法[6]。在此基础上,又出现了很多改进的版本。在K-均值算法中,数据点被分配到一个确定的聚类中,这也称为硬聚类;而模糊C均值聚类[7]是对K-均值算法的改进,是软聚类的典型代表,它不仅把一个数据点分配给一个或几个聚类,而且给出属于某个聚类的概率值[8]。另一个改进版本是k-Medoids算法[9],由于它在对噪声以及异常值(离群值)处理方面的优异能力,因而具有较强的鲁棒性[10]。在这几种算法中,从计算效率和稳定性来讲,K-均值算法仍然是最优的[11]。然而,K-均值聚类算法也存在2个主要的缺陷:其一是使用算法的前提条件是用户必须知道数据的聚类数量K,这在实际应用中是不现实的;其二是聚类结果对算法的随机初始划分非常敏感[12],因而可能造成聚类效果变差,甚至使聚类失败。正是这些因素影响算法对数据的聚类质量,因此,本文中提出相应的解决方案。为提高聚类性能,对原数据进行标准化预处理使其服从正态分布,利用监督的线性辨别分析(linear discriminant analysis,LDA)[13]对高维数据进行压缩(降维);通过对K-均值算法随机初始化的改进,使得对初始聚类中心的划分能避免空聚类并确保数据的可分离性;对聚类结果采用轮廓分析(silhouette analysis)[14],直观地评价算法的聚类质量,以确定数据固有的聚类数量。
1 数据预处理
在聚类问题中,假设p维数据的样本数量为n,则观测数据矩阵X一般可表示为
(1)
式中:X的每一行表示一个样本,每一列就是特征列即数据的属性(或变量),特征数量就是数据的维数。聚类的基本思想是根据数据之间的相似度(或距离)来划分数据,在聚类分析中,采用欧几里得(欧氏)距离来测度数据的远近。考虑到不同的特征取值之间的差别可能很大,甚至不在同一个数量级上;为提高算法的性能,通常要进行特征缩放的预处理, 使得不同特征处于同样的尺度上。典型的缩放有归一化和标准化[12]。数据特征的标准化为
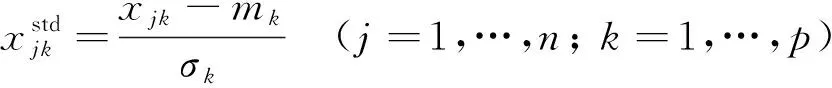
(2)
式中:xjk为数据点xj的第k个特征;mk和σk分别为第k个特征列的均值和标准差。经过标准化后的特征服从正态分布。标准化既能保留数据中离群值的有用信息,也能有效降低优化算法对噪声与异常值的敏感性[11]。
另一种数据预处理是对高维数据的降维,包括主分量分析[15]、核主分量分析[16]以及LDA等。考虑到数据经过标准化处理后具有正态性,而监督的LDA方法的假设条件正是数据服从正态分布,且各聚类的协方差矩阵是相同的。因此,本文采用LDA方法对数据进行预处理以实现数据压缩。
设数据X的固有聚类数量为K,某个聚类Ck(k=1,2,…,K)的质心(中心或均值)mk(k=1,2,…,K)定义为
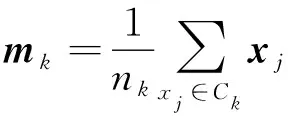
(3)
式中:nk为聚类Ck中的样本数量。同样地,定义来自各个聚类中所有数据样本总的均值m为
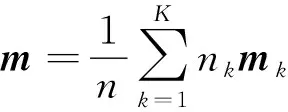
(4)
式中:n为数据X中全部样本的总数。
对聚类Ck,其散射矩阵(scatter matrix)[13]为
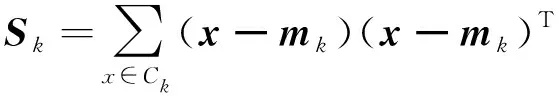
(5)
把所有聚类Ck(k=1,2,…,K)对应的散射矩阵Sk加起来就构成了类内(within-class)散射矩阵
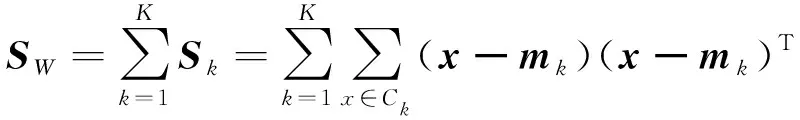
(6)
式中:散射矩阵Sk和SW都是p×p维方阵。对于实值的观测数据,散射矩阵一般是非奇异的,因而它们存在逆矩阵。
同样,类间(between-class)散射矩阵[17]为
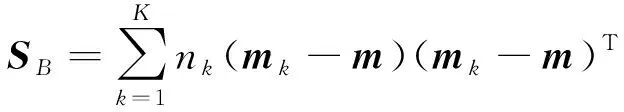
(7)
在此基础上,本文定义一个增广矩阵G,它由类内散射矩阵SW的逆和类间散射矩阵SB相乘:
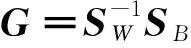
(8)
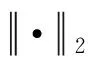
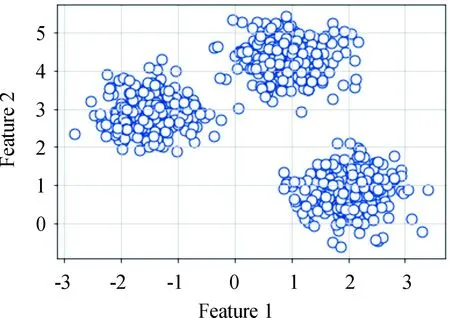
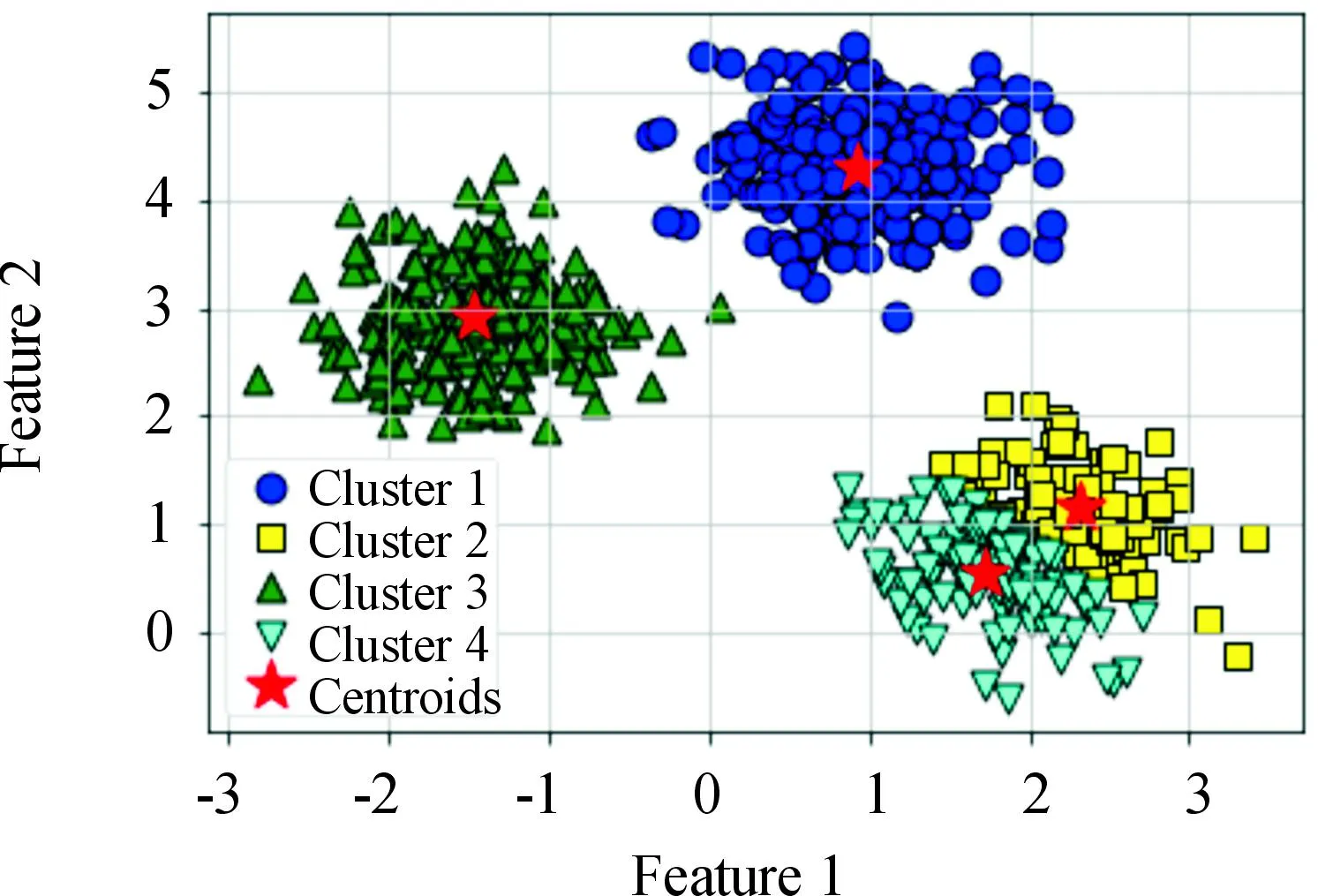
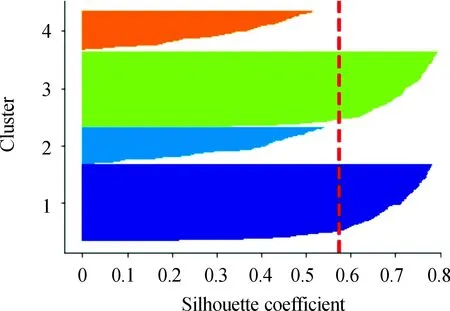
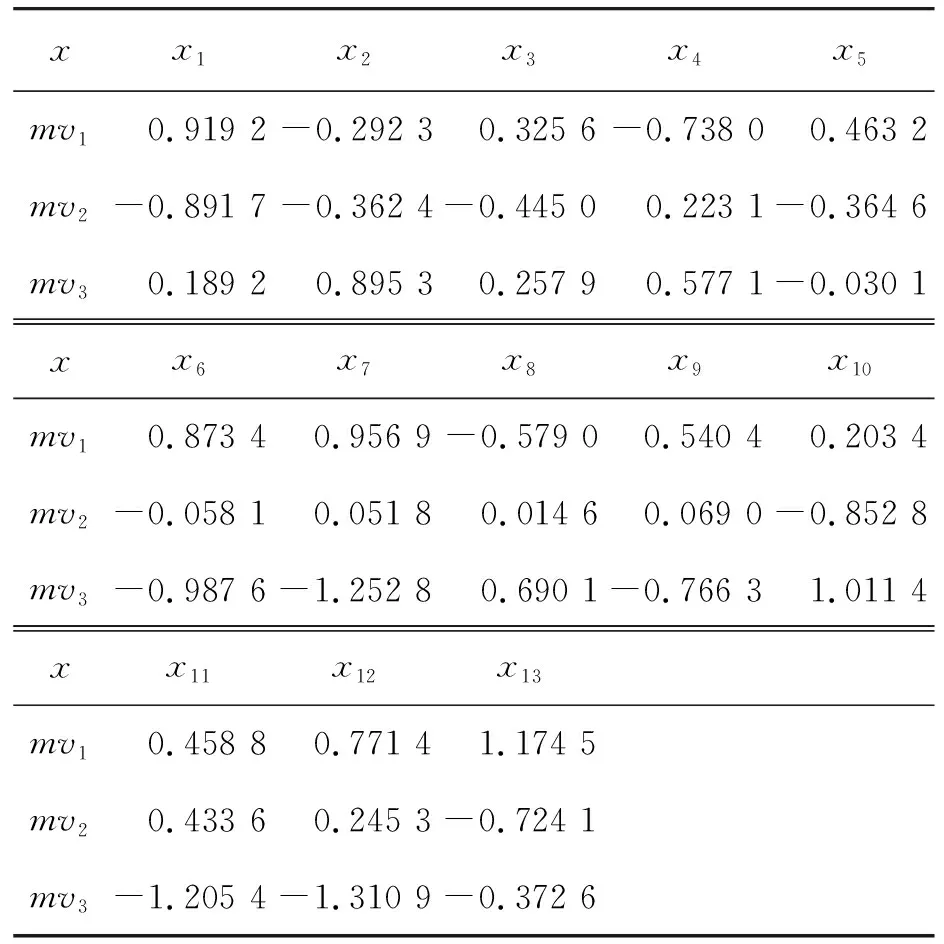
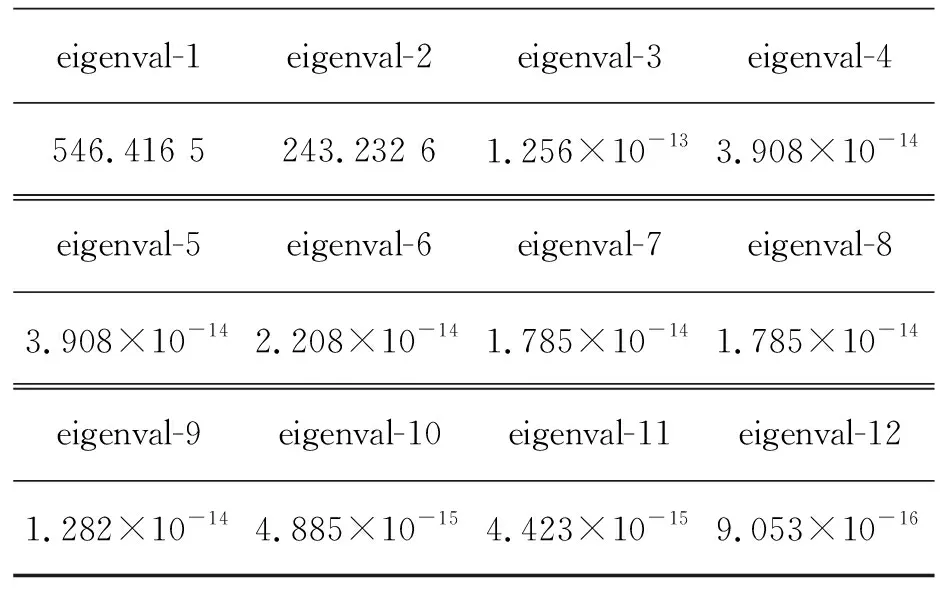
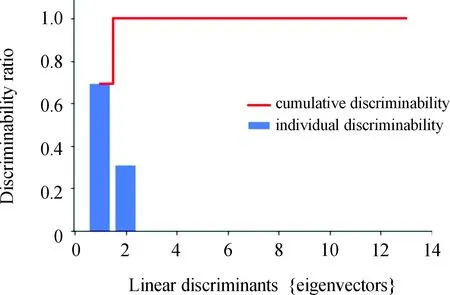
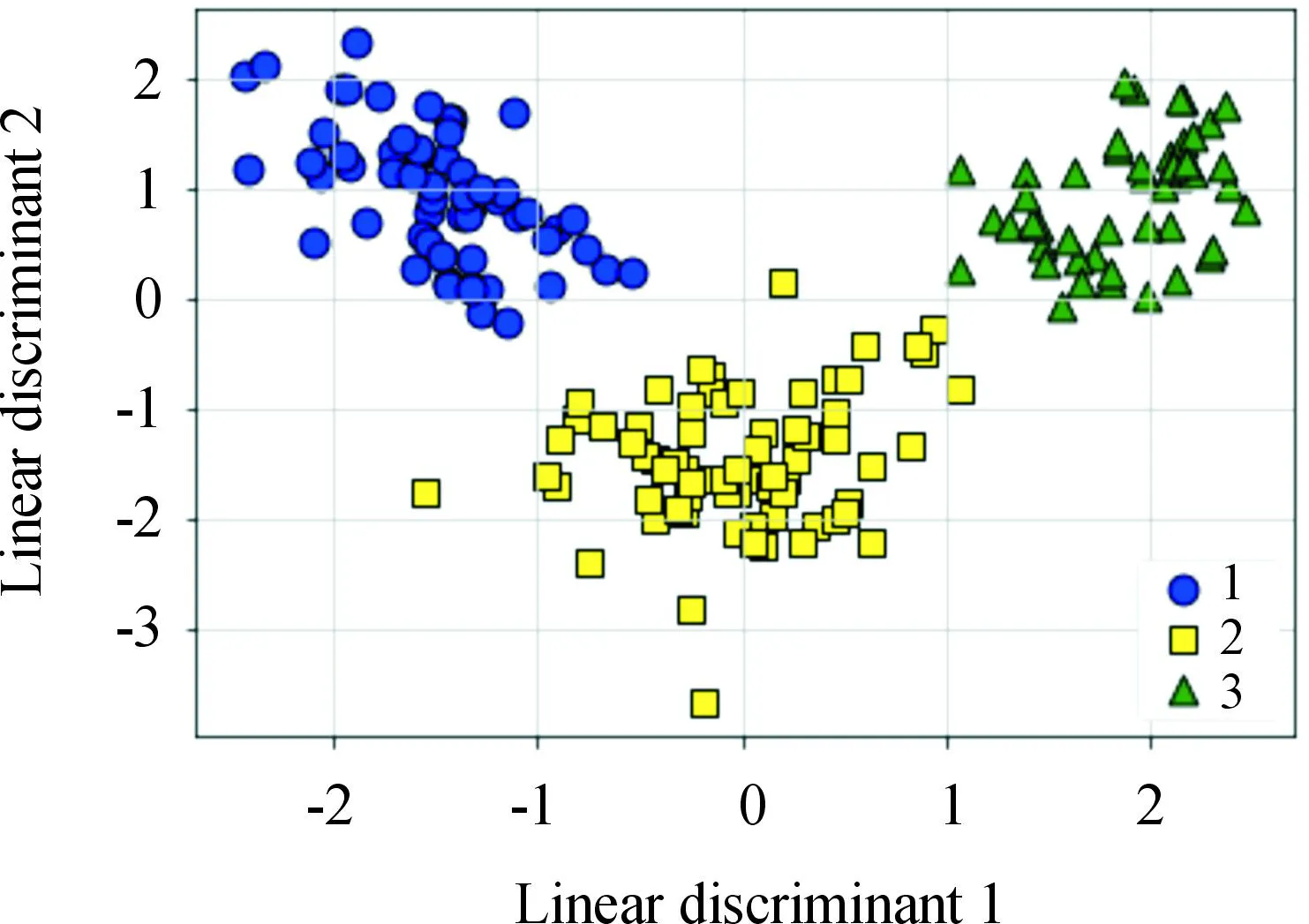
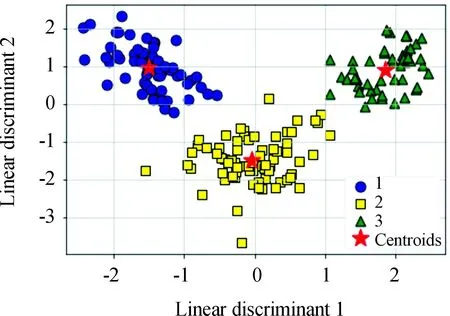
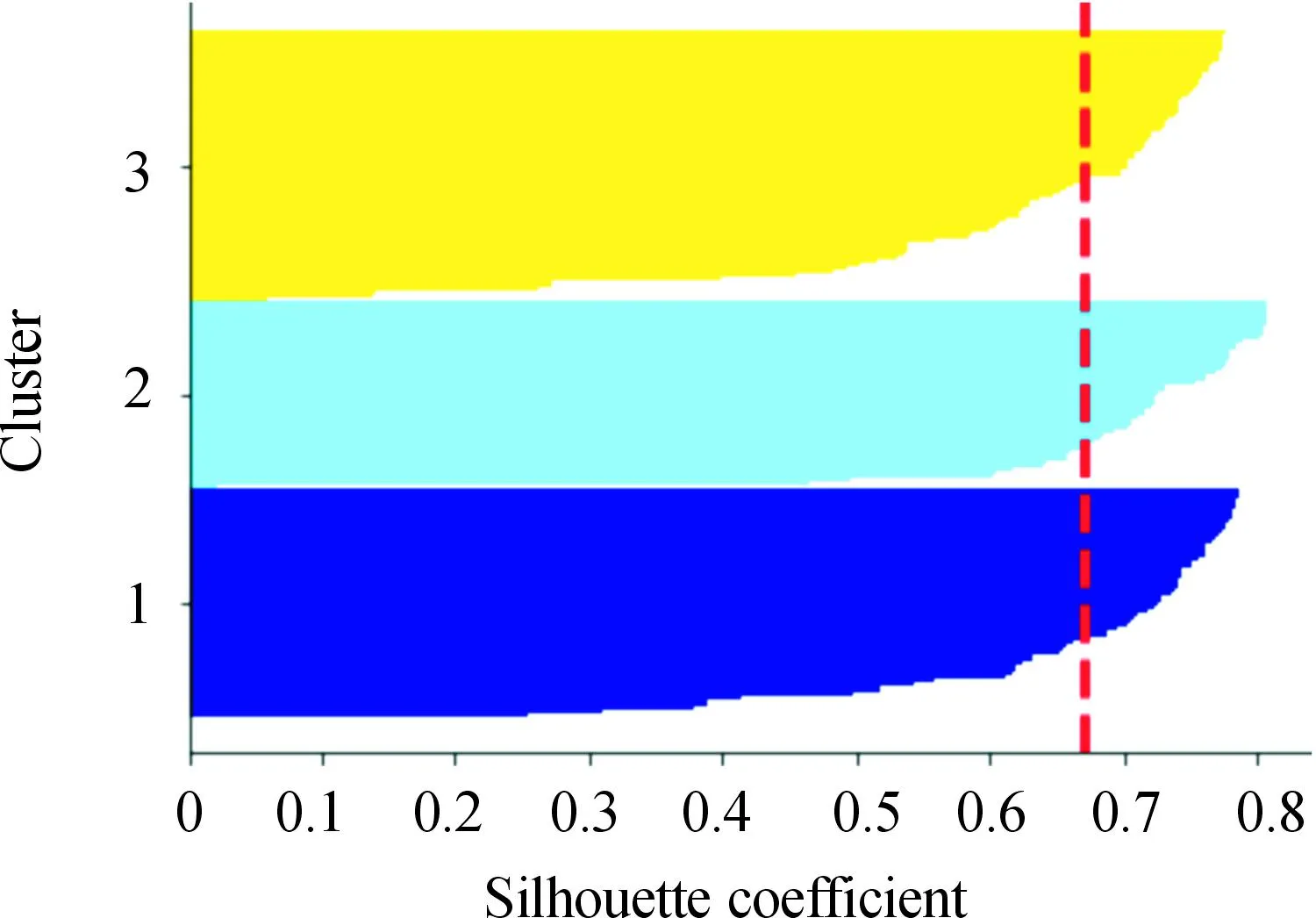
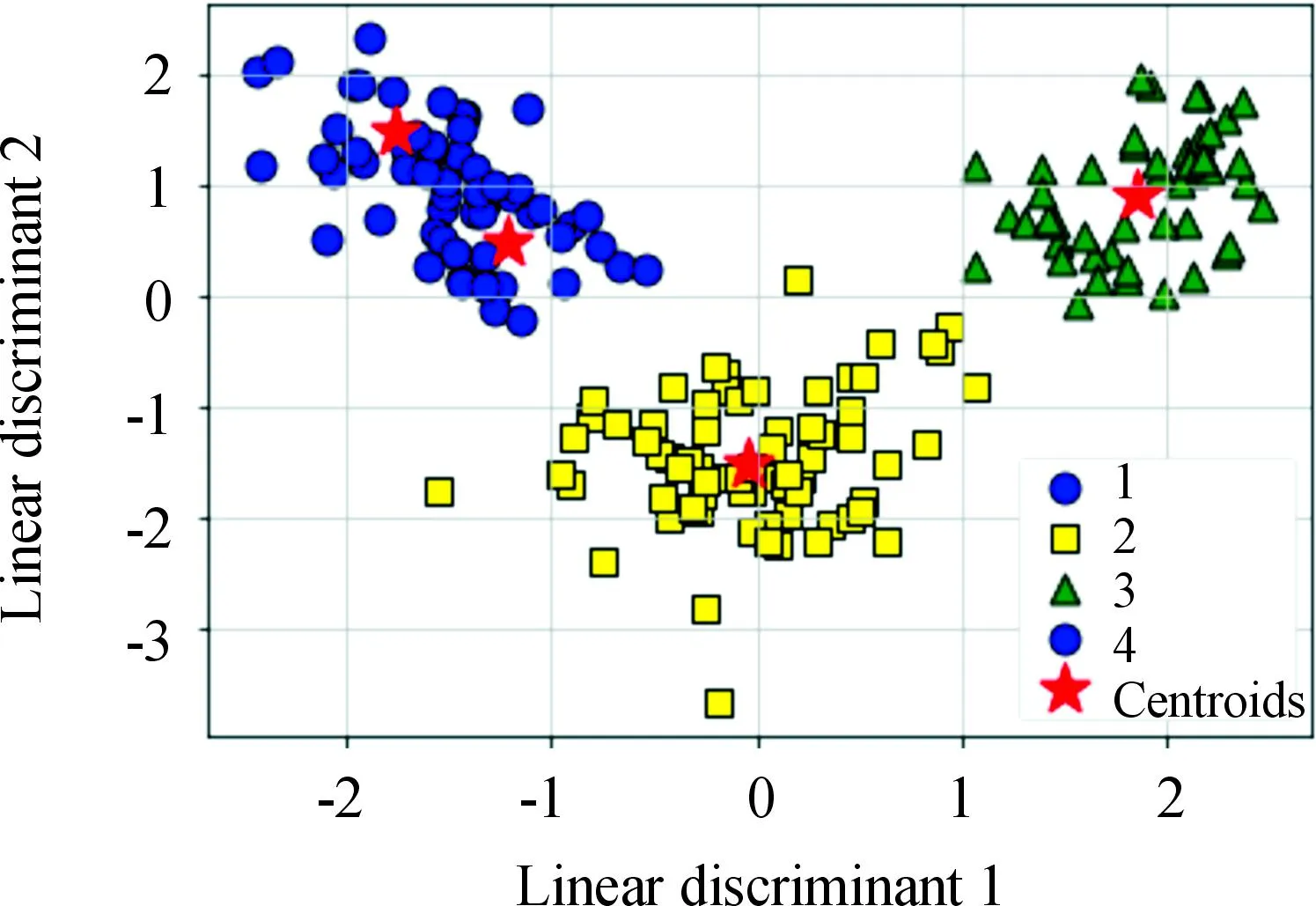
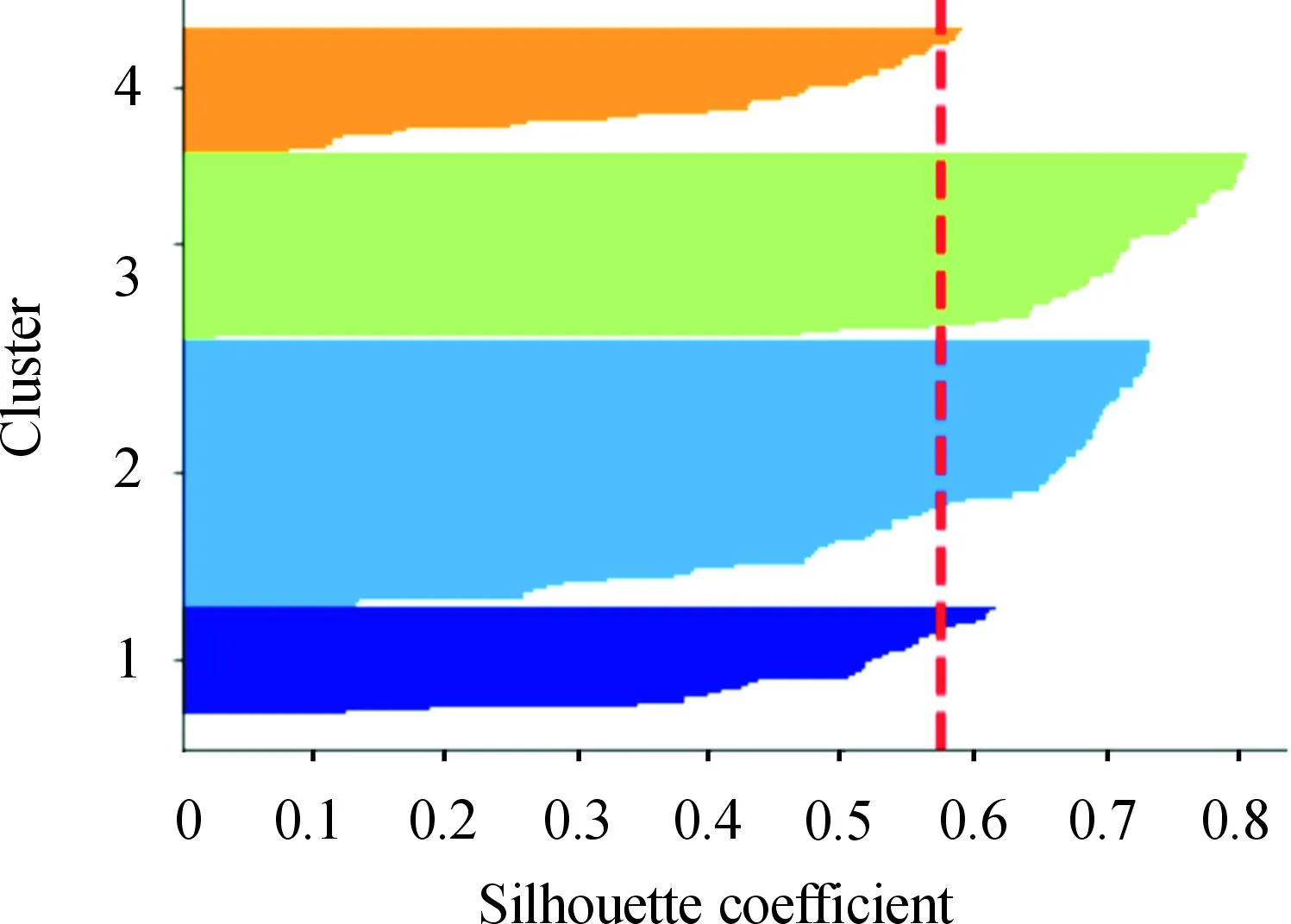
对矩阵G进行特征分解[18],即分解为特征值和其对应的特征向量,并将特征值按照从大到小的次序排列。对于具有K个聚类的数据集X,由类间矩阵SB的定义可知,它是由秩为1或秩为小于1的K个矩阵之和所构成的,因而它生成的线性辨别量(linear discriminants)的个数最多只能为K-1个[19]。在实际应用中,只有很少的几个最具辨别性的特征向量(对应于非零特征值)被抽取,假设抽取了v个(v< (9) 式中:E1是取值为最大的特征值所对应的特征向量;E2是对应于第二大特征值的特征向量,以此类推。 将观测数据矩阵X乘以变换矩阵W,也就把原始的数据X映射到一个v维的特征子空间上: Xsub=XW (10) 显然,上式是将原始的p维数据变换为(更低的)v维数据,即利用LDA实现了数据的降维。 经典的K-均值算法的基本迭代步骤[6]如下。 步骤1:从数据样本中随机指定K个数据点作为初始的聚类中心(即质心)mk(k=1,2,…,K)。 步骤2:将其他数据样本分配给邻近的质心,形成K个聚类Ck(k=1,2,…,K)。 步骤3:根据当前数据所在的聚类,重新计算(更新)每个聚类中数据的质心(即按照式(3)计算)。 步骤4:重复步骤2和步骤3,直到聚类中心不再变化, 或达到用户指定的最大迭代次数,或达到用户指定的误差容限。对于划分聚类,常用的误差度量就是平方误差和(sum-of-squared-error,SSE)[20]: (11) 由于初始质心选择是随机的,一些质心之间的距离可能会太近,因而在后面的迭代中被合并, 造成空聚类。为解决此问题,提出改进的K-均值聚类算法,其主要流程如下。 1) 计算任意2个样本点的欧氏距离,并把距离最远的2个点(设为x1和x2)作为初始的2个质心。 D(x1,x2)=max{D(xi,xj)}(i,j=1,2,…,n) (12) 式中:D(x1,x2)为数据点x1和x2之间的欧氏距离。 2) 在1)的基础上,第3个聚类中心x3的选取则遵循最小-最大规则 min{D(x3,xr),r=1,2}= max{[D(xi,xr),r=1,2],i≠1,2} (13) 即x3与(x1,x2)的距离中的最小者为其他数据点xi(i≠1,2)与(x1,x2)的距离中的最大者。 3) 在1)和2)选定的数据点(x1,x2,x3)的条件下,仍利用最小-最大规则,依此可获得初始的K个聚类中心。 显然,经过以上的处理,就确保了初始聚类中心之间是完全可分的,避免出现空聚类,也使得算法有一个合理的初始划分,从而解决了经典K-均值算法的步骤1中对随机初始化敏感的问题。然后继续经典K-均值算法的步骤2—4即可实现对数据的聚类分析。本文中将经过改进后的算法仍称为K-均值算法。 要验证聚类结果是否反映数据的固有结构,需要对聚类的质量进行客观评价。轮廓分析就是一种能对聚类结果进行直观评估的方法。 对于给定聚类Ci中的数据点xi,定义ai为 (14) 称ai为聚类凝聚力[21]。若xi是Ci中唯一的数据点, 则ai=0;否则,ai为点xi到Ci中其他数据点的平均距离。ai的取值表示xi与它所在聚类中其他数据点的相似程度。 一个给定聚类Ci中的数据点xi到其他聚类Ck(k≠i)中数据点的平均距离定义为 (15) 基于平均距离bik,聚类分离性bi定义[21]为 (16) 即bi是数据点xi到与它最邻近的那个聚类中所有数据点的平均距离。显然,bi的取值是表示某个聚类中数据点与其他聚类中数据点的相异程度。 对于每一个数据点xi,定义其轮廓系数[22]为 (17) 显然,轮廓系数si的取值范围为[-1,1]。若bi与ai的取值相等,bi=ai,则可得si=0,即聚类质量差;相反,若bi与ai差值很大,bi>>ai,则得到si≈1,即表示聚类质量高。每个聚类的轮廓用于表示该聚类中样本之间的紧密程度。 数据集X中所有样本的平均轮廓系数S为 (18) 平均系数S用于辨识各聚类中是否包含异常值,且可推断聚类结果,S值越大,聚类质量越高。 对好的聚类结果,各聚类的轮廓系数应具有大致相同的尺寸[22]。因此,实际应用中可通过对聚类的轮廓进行视觉检查来评价聚类的质量。 为验证本文方案的有效性,利用2个不同类型的数据集进行仿真。通过输入不同K值,比较聚类结果以确定数据集本身所固有的聚类数量。 仿真在个人计算机(PC)上进行。采用的操作系统为Windows 10,编程使用Python 3.8。 在这个仿真中,采用具有2个特征的Blob数据集,其由600个样本点形成3个簇(各含200个数据点,用圆圈表示)。横轴表示特征1,纵轴表示特征2,该数据的二维散点图如图1所示。 图1 数据集Blob的二维散点 3.1.1 指定聚类数与数据固有聚类数相同 对于Blob数据集,利用K-均值算法进行聚类,主要参数设置如下:指定聚类数量K=3,这也是数据本身的聚类数量;算法的最大迭代次数为max_iter=300。这里需要说明:实际应用中,若在最大迭代次数之前算法已收敛,则迭代就停止。相反,算法可能在某次运行中不收敛,这时若选择更大的迭代次数,则算法的计算成本将增加。为此,本文附加另外一个参数,即误差容限(tol)来控制算法的收敛条件。在以下仿真中,统一设置一个较大值:tol=0.000 1。 在以上参数的条件下,K-均值算法对数据的划分以及对聚类质心的辨识结果如图2所示。 图2 在给定K=3时Blob数据的聚类结果 在图2中,不同聚类中数据点用不同的形状和颜色表示。可以看出,3个聚类的质心(红色五角星表示)被放置在每个数据堆的中心位置,该点不一定是某个数据点,可能是几个数据点之间的点。显然图2的结果与数据集Blob的自然划分完全一致,因此聚类效果很好。 为了直观地分析聚类结果中每一类数据的紧凑性,绘制出每个聚类对应的轮廓系数如图3所示。 图3 在给定K=3时Blob数据簇的轮廓系数 从图3可以看出,3个聚类的轮廓具有大致一样的宽度和长度;且所有样本的平均轮廓系数(图中用红色虚线表示)的值超过了0.7(即远离0值),这意味着聚类效果良好。 小结:综合图2和图3的结果可知,如果指定数据集的真实聚类数量作为算法的参数,则算法在这个Blob数据集上提供了优良的聚类质量。 3.1.2 指定聚类数小于数据固有聚类数 若用户指定的聚类数量小于数据本身的聚类数量,例如指定算法的聚类数量为K=2,则聚类结果的散点图和轮廓系数分别如图4和图5所示。 图4 在给定K=2时Blob数据簇的聚类结果 图5 在给定K=2时Blob数据簇的轮廓系数 从图4可以看出,在上部原本的两堆数据被强行地合并成一个聚类;而在图5中Cluster1的轮廓系数正是由原来2个聚类轮廓合并而成的,而且全部数据的平均轮廓系数比图3也降低了10%以上。 小结:综合图4和图5的结果可知,如果指定的聚类数量小于数据集原本的聚类数量,其聚类结果发生扭曲,聚类质量变差。 3.1.3 设置聚类数大于数据固有聚类数 若指定算法的聚类数量大于数据固有的聚类数量,例如设置聚类数量为K=4,则聚类的散点图和相应的轮廓系数如图6和图7所示。 图6 在给定K=4时Blob数据簇的聚类结果 图7 在给定K=4时Blob数据簇的轮廓系数 从图6可以看出,右下角的数据被算法强行拆分成2个聚类;图7中,Cluster2和Cluster4的轮廓系数正是图6中被拆分的2个聚类所对应的轮廓,而且整个样本数据的平均轮廓系数与图3相比较,下降了15%左右。 小结:图6和图7的聚类结果说明,若设置算法的聚类数量大于数据固有的聚类数量,则产生的聚类质量急剧下降。 通过对Blob数据集的仿真可知,无论是对聚类数量K的过高或过低估计,都将对聚类结果产生影响,致使聚类形状畸变、聚类效果恶化。 在下面的仿真中,使用著名的UCI机器学习数据库中真实的红酒(Wine)数据集。该数据集是对意大利同一地区种植,但来自3种不同品种的葡萄酒进行化学分析得出的数据。Wine给出这3种葡萄酒的13种不同成分的含量,不同成分就是数据的特征。它们分别为酒精(表示为x1)、苹果酸(x2)、灰(x3)、灰分碱度(x4)、镁(x5)、总酚(x6)、黄酮素类化合物(x7)、非黄酮类酚类(x8)、原花青素(x9)、颜色强度(x10)、色调(x11)、稀释葡萄酒的OD280/OD315(x12)以及脯氨酸(x13)。 3.2.1 高维数据集Wine聚类的主要步骤 ① 对13维的Wine数据集标准化。 ② 对于每个类(葡萄),计算13维均值向量。 ③ 构建散射矩阵SB和SW,计算增广矩阵G。 ④ 将矩阵G分解为它的特征值和特征向量。 ⑤ 按降序对特征值进行排序,从而对相应的特征向量进行排序。 ⑥ 选择对应于v(v<13)个最大特征值的v个特征向量来构造13×v维变换矩阵W;所选定的特征向量就是变换矩阵W的列。 ⑦ 使用变换矩阵W将原始数据集投影到新的特征子空间上。 ⑧ 在特征子空间上,对变换后的数据进行聚类。 3.2.2 Wine数据集的降维 Wine数据集共有178个样本,每一类葡萄酒的样本数量分别为59、71、48。3种葡萄酒的类标签分别表示为1、2、3。为了观察不同特征的取值的差异性,表1给出所有样本的13个特征的均值(m)和标准差(σ)。 表1 Wine数据集全部样本的13个特征均值与标准差 从表1可以看出,特征x8和特征x13的均值之间相差达2 064倍,而标准差之间相差达2 529倍。这反映了不同特征所包含的信息是不同的。如果考虑所有特征,则会给计算带来大的负担。因此,利用LDA对Wine数据集进行降维,以找出对聚类最具有辨别性的少数几个特征。 首先对Wine数据集进行标准化预处理,然后对每一类葡萄酒的13个特征,计算出其相对应的均值向量(mv),结果如表2所示。 表2 标准化后Wine数据的均值向量 构造矩阵SB和SW并计算增广矩阵G,对其进行分解,可获得特征值、特征向量。将特征值按照由大到小的次序排列,结果如表3所示。 表3 降序排列的12个特征值 第13个特征值为0。从表3可以看出,从第3到第12个特征值虽然不为0,这是由于Python语言浮点数的表现形式,但实际上它们取值都为0。换句话说,除了前2个特征值是明显的非零值之外,其余特征值均为0。 在LDA中,特征向量代表与聚类有关的辨别信息,其内容称为可辨别性(discriminability)。为了测度每个特征向量所包含的辨别性信息,将特征值按照降序排列,并按照同样次序绘制出对应的线性辨别量(即特征向量)以及累计(cumulative)的可辨别性的图形,其结果如图8所示。 图8 Wine数据集13个特征的可辨别性 从图8可以看出,仅前2个特征向量就获得了Wine数据集累计100%的辨别信息。因此,把这2个特征向量列叠加起来即可得到变换矩阵W。 利用变换矩阵W将原始的13维Wine数据X进行变换:Xsub=XW,则得到新的2维特征子空间。数据Xsub在2维空间的散点图如图9所示。 图9 数据集Xsub在2维子空间的散点 从图9可以看出,由2个线性辨别量(linear discriminant)构成的2维特征子空间中,变换后的数据Xsub形成了3个自然的数据簇,且各聚类之间是完全可分离的。这意味着利用2个线性辨别量进行聚类分析也不会损失原本数据的有关信息,即本文采用的LDA对数据的降维是非常有效的。 3.2.3 降维后数据集的聚类分析 在2维的数据集Xsub基础上,利用K-均值算法对其进行聚类分析。这里仅考虑算法的指定参数K与数据集原始聚类数量是否相等2种情况。 1) 指定聚类数与数据固有聚类数相同 当正确地设置K-均值算法的聚类数量为K=3时,对变换后的数据Xsub进行聚类,其结果的散点图和轮廓系数如图10和图11所示。 图10 在给定K=3时数据Xsub的聚类结果 图11 在给定K=3时数据Xsub聚类的轮廓系数 从图10可以看出,3个聚类的质心被准确地定位在每一堆数据的中心。从图11也可以看出,3个聚类的轮廓尺寸略有不同,这是由于3种葡萄酒的样本数量各不相同所致。但从总体上来看,3个聚类的轮廓具有大致相同的长度和宽度,表现为相互之间较为协调。另外,从图11还可以看出,数据集Xsub全部样本的平均轮廓系数值接近于0.7,说明聚类质量较高。 小结:综合图10和图11的聚类结果可知,对Wine数据集采用LDA降维后,在2维的特征子空间上,若指定K-均值算法的参数K等于数据集的固有聚类数量,则聚类效果很好。 2) 指定聚类数与数据固有聚类数不同 尽管Wine数据集本身具有类标签,即聚类数量事先是已知的。但在实际应用中,一般的数据集的聚类结构是无法得到的,因此对于未知的聚类数量的确定(估计)并不容易。 如果对K-均值算法指定的聚类数量K与数据集Xsub本身的聚类数量不相符,例如:假定设置算法的参数K=4,则对应的聚类结果的散点图以及轮廓系数如图12和图13所示。 图12 在给定K=4时数据Xsub的聚类结果 图13 在给定K=4时数据Xsub聚类的轮廓系数 从图12可以看出,左上角数据被算法强制地划分为2个聚类。这种划分造成了聚类结构的复杂化,使得对其结果的解释更为困难。 从图13可以看出,Cluster1和Cluster4的轮廓尺寸明显小于其他2个聚类的轮廓,这正是反映了图12中被强制划分成2个新的聚类所对应的轮廓。另外,在图13中,所有样本的平均轮廓系数也被降低到小于0.6,与图11相比较,平均轮廓系数大约降低了10%左右,即聚类质量变差。 小结:综合图12和图13的结果可知,若指定K-均值算法的参数K不等于数据集Xsub的固有聚类数量,则聚类效果明显恶化。 从以上对现实数据集Wine的仿真可知,在未知数据集固有聚类结构的情况下,估计的聚类数量是否正确,直接决定聚类的效果和聚类的质量。 为了解决划分聚类(经典的K-均值)算法需要用户事先指定聚类数量的缺陷,本文进行了相关的研究。对于算法的随机初始化问题,利用最小-最大规则对其进行改进,避免算法出现空聚类并确保数据的可分离性。对于现实世界真实的数据集,利用标准化预处理使之服从正态分布,并利用监督的线性判别分析LDA用于抽取高维数据中所包含对聚类最具辨别性的特征,以实现数据降维。通过计算各聚类的轮廓系数并比较其尺寸,利用轮廓分析法评估聚类质量。本文方案的主要贡献体现在:对于复杂的数据集,由于估计准确的聚类数量是很困难的,为此可采用LDA对数据降维,通过估计未知数据集的聚类数量K的大致范围,然后对不同K值的聚类质量进行可视化检查,从而为各种划分聚类算法提供原数据的固有聚类数量。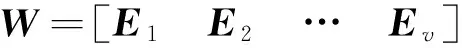
2 初始化改进与聚类质量评价
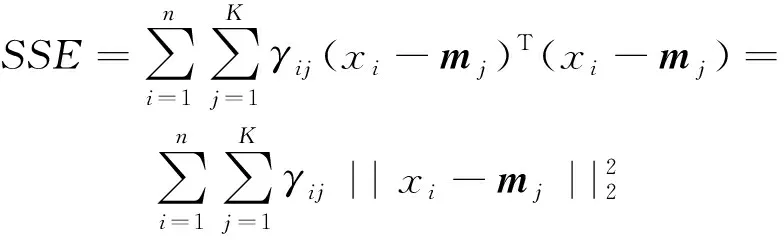
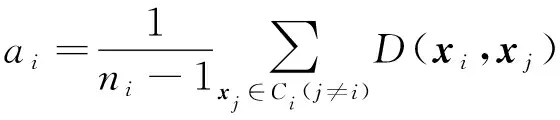
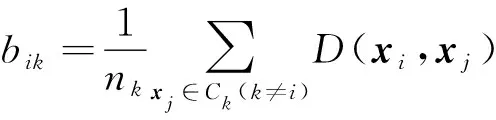
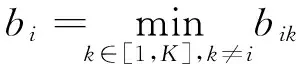
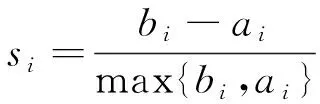
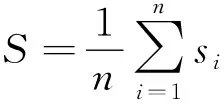
3 仿真结果与分析
3.1 二维数据集
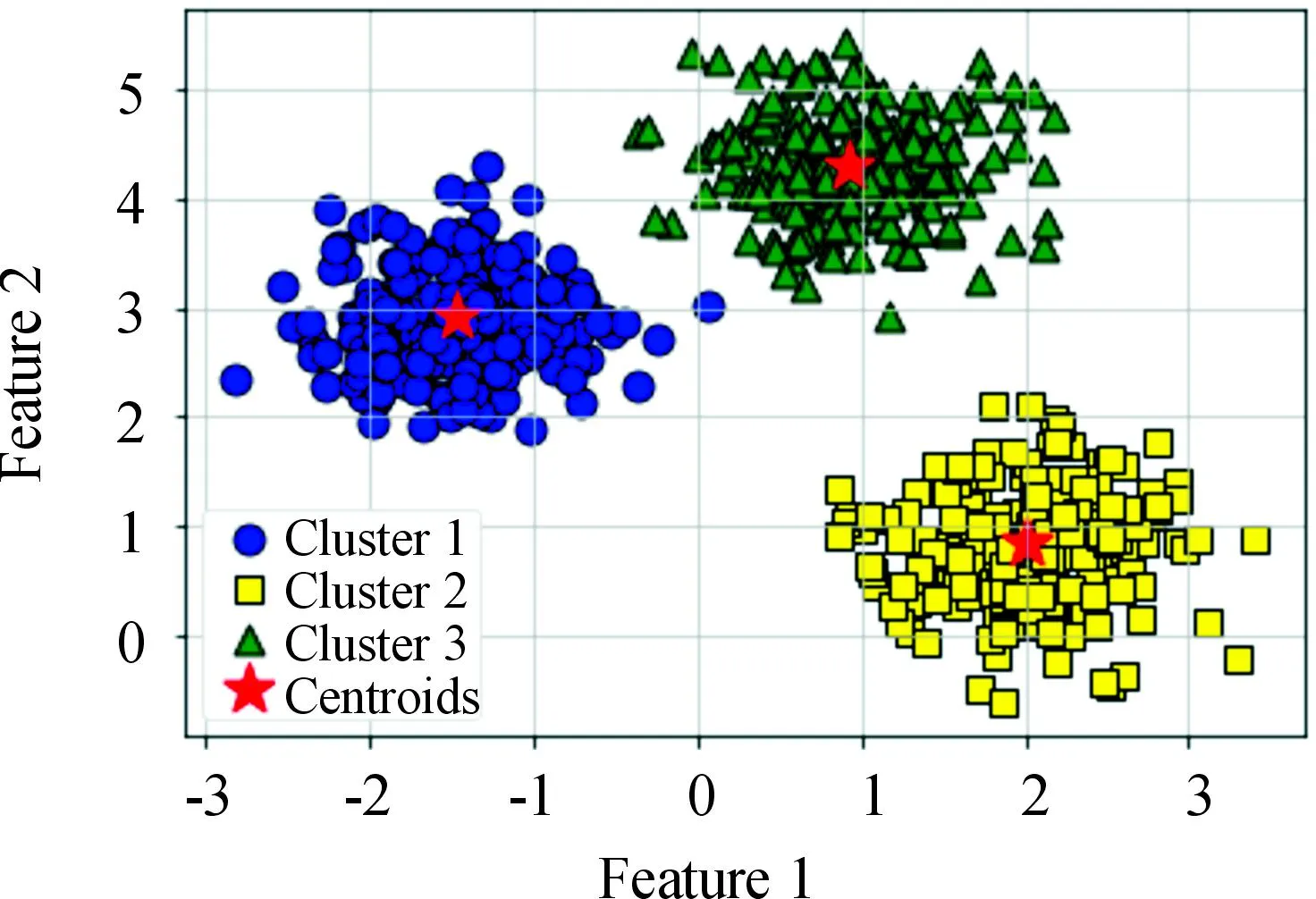
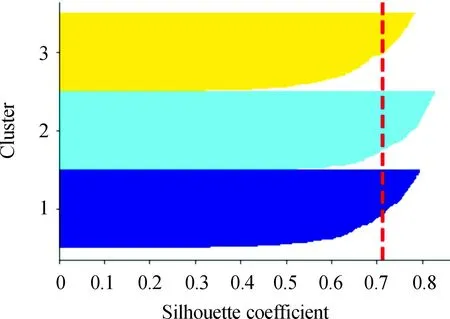
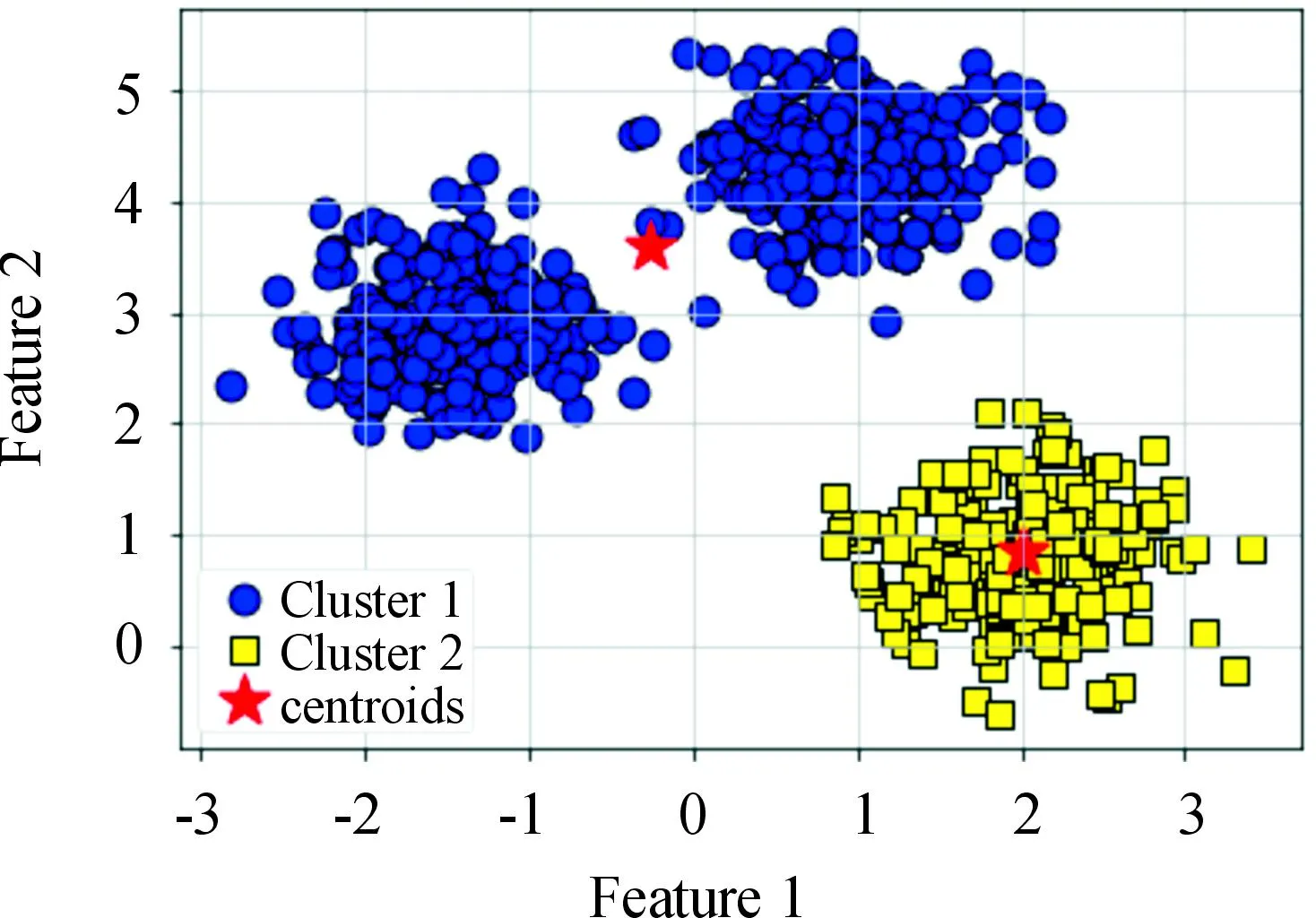
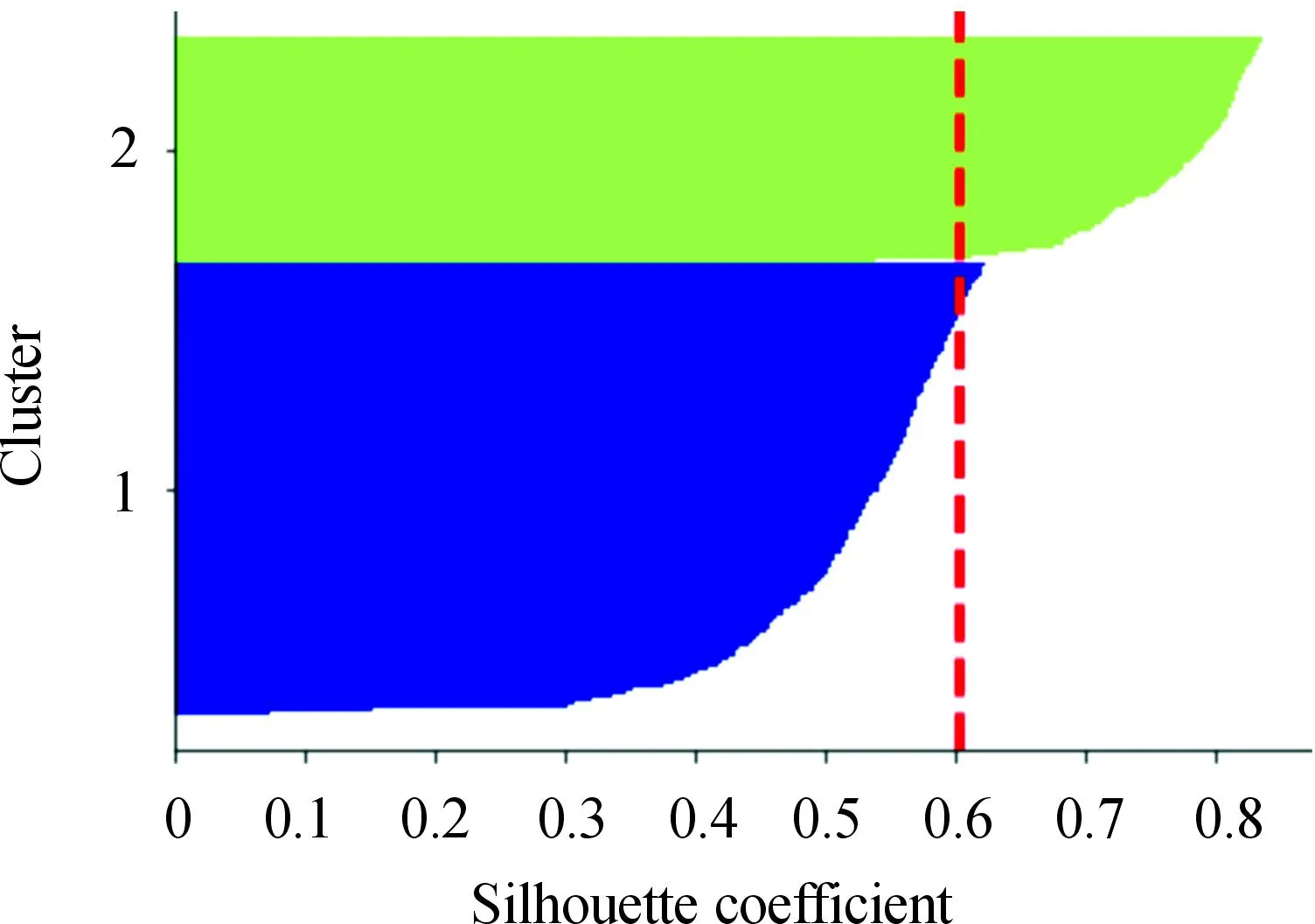
3.2 高维数据集

4 结论
