求解函数优化和特征选择的改进金豺狼优化算法

邹 睿,焦 慧,龙 文

(1. 上海工程技术大学 电子电气工程学院, 上海 201620;

0 引言

为了找到复杂问题的最优解,各种工程领域都需要优化技术。优化的主要目标是找出一组决策变量的最优解,从而使目标函数最小化或最大化。近几十年来,元启发式算法在处理各种工程领域的复杂优化问题方面越来越受欢迎,原因在于它比传统的数值方法成本更低、效率更高,并已在许多领域如特征选择、泊位分配、参数估计、车间调度、多目标优化中得到有效应用。大多数元启发式算法都源于自然灵感,可以分为基于进化的、基于群体的、基于物理的或基于数学的。一些流行的元启发式算法包括:遗传算法(Genetic Algorithm, GA)[1]、粒子群优化(Particle Swarm Optimization, PSO)算法[2]、灰狼优化(Grey Wolf Optimizer, GWO)算法[3]、海鸥优化算法(Seagull Optimization Algorithm, SOA)[4]、均衡优化(Equilibrium Optimizer, EO)算法[5]、正弦余弦算法(Sine Cosine Algorithm, SCA)[6]等。

金豺狼优化(Golden Jackal Optimization, GJO)是最近开发的一种基于群体的元启发式算法,其灵感来自CHOPRA等[7]于2022年提出的金豺狼的协作狩猎行为。GJO算法具有较强的全局优化能力、较少的控制参数和容易编程实现,在无限脉冲响应系统辨识[8]、图像分割[9]、电力故障诊断[10]、软件故障预测[11]、参数优化[12]、燃料电池模型参数估计[13]等领域中得到广泛的应用。

然而,与其他元启发式算法一样,基本GJO算法在处理复杂优化问题时也会存在局部开发能力差、容易陷入局部最优区域、勘探和开发能力不平衡等缺点[14]。为了提高基本GJO算法的优化精度和收敛速度,MOHAPATRA等[14]提出了一种基于快速随机反向学习的改进GJO算法。YUAN等[15]设计一种新颖的双黄金螺旋位置更新规则以改善优化效率,引入动态透镜成像学习算子以增加群体多样性,提出一种混合版GJO算法。ARINI等[16]提出了一种基于联合反向选择的增强型GJO算法。新算法利用动态反向学习算子,增强种群多样性和嵌入选择性领导反向学习机制加快收敛,从而达到平衡探索和开发的目的。SNEL等[17]采用反向学习方案提高Pareto最优解的覆盖率,引入一种基于精英的引导策略,引导最优金豺狼个体在搜索空间内寻找有希望的区域,提出一种有指导的多目标GJO算法。

尽管上述改进算法通过引入新的机制或设计新的算子来提高GJO的性能,但它们的搜索效率需进一步加强。另外,无免费午餐(No Free Lunch, NFL)定理[18]指出,没有任何一种元启发式算法能解决所有类型的优化问题。因此,开发一种新的或改进现有的元启发式算法已成为优化领域的研究热点问题之一。

本文设计一种新的非线性逃脱能量因子以平衡探索和开发,引入翻筋斗学习策略以避免算法陷入局部最优,进而提出一种改进的GJO(I-GJO)算法。基准函数优化和特征选择问题的实验结果表明,I-GJO算法的性能有明显的提高。

1 金豺狼优化算法

金豺狼优化(GJO)算法是模拟自然界中金豺狼群体合作捕猎食物行为的一种新型优化技术。与其他元启发式算法一样,GJO在进行迭代搜索之前,需在解空间中随机产生一组解,构成初始群体:

X0=Xmin+rand·(Xmax-Xmin),

(1)

式中:X0为金豺狼群体的初始位置,rand为[0,1]间的随机数,Xmax、Xmin分别为变量的上、下边界。

金豺狼知道如何感知和跟踪猎物,但有时猎物不容易捕食或容易逃脱。首先需计算猎物逃脱能量E的大小:

E=c1·(1-t/T)·E0,

(2)

式中:c1是一个常数,t和T表示当前和最大迭代次数,E0=2r1-1表示猎物逃脱初始能量,r1为[0,1]间的随机数。

当|E|>1时,金豺狼群体进入搜索猎物阶段(探索阶段),搜索过程由雄性豺狼主导,雌性豺狼跟随雄性豺狼行动,其数学模型为:

X1(t)=XM(t)-E·|XM(t)-rL·Xp(t)|,

(3)

X2(t)=XFM(t)-E·|XFM(t)-rL·Xp(t)|,

(4)

X(t+1)=(X1(t)+X2(t))/2,

(5)

式中:XM和XFM分别表示雄性豺狼和雌性豺狼的位置,rL为基于Levy飞行产生的随机数[7],Xp表示猎物的位置。

猎物受到金豺狼的骚扰,其逃脱能量降低。当|E|≤1时,金豺狼群体进入包围、攻击猎物阶段(开发阶段),雄性豺狼和雌性豺狼一起狩猎,这种行为的数学模型为:

X1(t)=XM(t)-E·|rL·XM(t)-Xp(t)|,

(6)

X2(t)=XFM(t)-E·|rL·XFM(t)-Xp(t)|,

(7)

X(t+1)=(X1(t)+X2(t))/2。

(8)

GJO算法的伪代码实现见文献[7]。

2 改进金豺狼优化算法

基本GJO算法在求解某些优化问题时,存在容易陷入迭代停滞、后期收敛缓慢、探索和开发能力不平衡等不足,在求解复杂优化问题时缺点更加明显[16]。为了提高基本GJO算法的搜索效率,本节提出两种新的改进策略,即非线性逃脱能量因子和翻筋斗学习机制。

2.1 非线性逃脱能量因子

探索和开发能力是所有元启发式优化算法在搜索过程中需要平衡的。探索一般发生在算法迭代前期,种群尽可能在解空间中广泛搜索,找到有潜力的区域,从而提高算法找到全局最优解的概率;开发则主要出现在算法迭代中后期,群体在解空间中找到的潜力区域进行“精细搜索”,进而加快收敛速度。

在GJO算法中,探索能力和开发能力的转换依赖于逃脱能量E,即|E|>1算法进入探索阶段,而|E|≤1则进入开发阶段。图1给出了基本GJO算法中逃脱能量E的变化趋势。

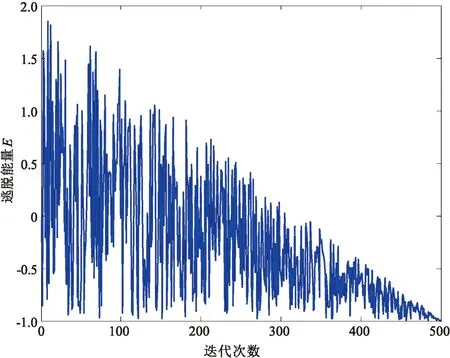
图1 基本GJO算法中E的变化

一般来说,GJO算法在迭代前期进行探索,为其找到全局最优解奠定基础,而在中后期执行开发阶段以加快收敛速度。然而,从图1可以观察到,基本GJO算法在搜索过程中随机进行探索或开发,且在迭代前期仅进行极少的探索过程,达不到平衡探索和开发能力的目的。因此,提出一种修改的逃脱能量E策略,其数学表达式为:

E=Emax-sin((t/T)2·π/2)·(Emax-Emin),

(9)

式中:Emax和Emin分别为E的最大值和最小值。图2给出了改进GJO算法中逃脱能量E的变化。

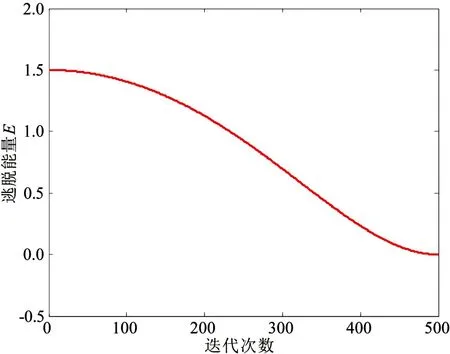
图2 改进GJO算法中E的变化

2.2 翻筋斗学习策略

翻筋斗觅食是蝠鲼在狩猎时最有效的一种方式,当找到食物源时,它们会做一系列向后翻筋斗动作,围绕浮游生物(猎物)旋转,将其吸引到自己身边。受这种捕食行为的启发,ZHAO等[19]提出了一种新的翻筋斗觅食策略用于元启发式算法中,具体描述如下:猎物的位置被视为一个支点,蝠鲼倾向于围绕枢轴和翻筋斗来回游动到新的位置。本文将翻筋斗觅食行为引入到GJO算法中,设计了一种翻筋斗学习策略,其数学表达式为:

X(t+1)=X(t)+S·(r2·XM(t)-r3·X(t)),

(10)

式中:S称为空翻因子,r2和r3分别为[0,1]间的随机数。翻筋斗学习策略示意图如图3所示。

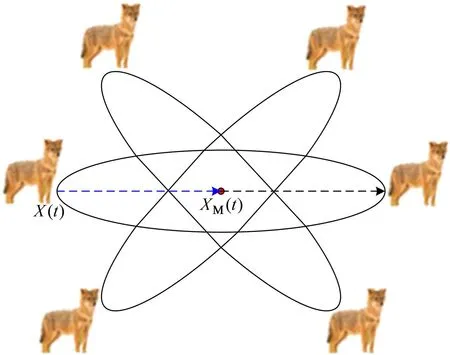
图3 翻筋斗学习策略

从图3可以看出,每只豺狼个体通过翻筋斗学习都可以移动到新搜索域中的任何位置,该搜索域位于当前位置与其围绕目前找到的最佳豺狼位置的对称位置之间。翻筋斗学习策略不仅可以改善群体多样性,还可以加快算法的收敛速度。

综上所述,改进GJO算法的流程图如图4所示。

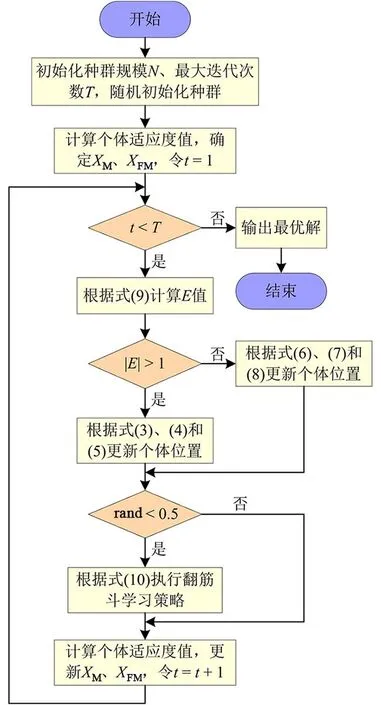
图4 I-GJO算法流程图

3 基于I-GJO算法的函数优化

为了验证I-GJO算法的有效性,从文献[20]中选取6个基准函数优化问题进行仿真实验。表1给出了6个问题的详细信息。表1中,f1、f2、f3是单峰函数,仅包含有一个全局最优值,通常用于测试元启发式算法的开发能力;f4、f5、f6是多峰函数,存在多个局部最优值,用来测试算法的探索能力。6个函数优化问题的理论最优值均为0。

表1 6个基准函数优化问题

I-GJO算法求解上述6个基准函数优化问题,所得结果与GWO算法[3]、SOA[4]和基本GJO算法[7]进行比较。在实验中,4种算法的种群大小均设为30,最大迭代次数为500。其他参数设置如下:在GWO中,a=2;在SOA中,fc=2;在GJO中,c1=1.5;在I-GJO中,Emax=1.5,Emin=0,S=2。每个基准函数优化问题的维数为30,4种算法对6个问题均进行10次实验以减少结果误差。

表2给出了GWO、SOA、GJO和I-GJO算法对6个函数优化问题10次实验的最优值、平均值和标准差结果比较。

表2 4种算法对6个问题的求解结果

从表2可知,I-GJO算法在6个优化问题上都能收敛到理论最优值,且具有较强的鲁棒性。与GWO、SOA和基本GJO算法相比,I-GJO算法在6个基准函数优化问题上均获得了较高的寻优精度。

图5给出了GWO、SOA、GJO和I-GJO算法对6个函数优化问题的迭代收敛曲线。从图5可以清晰地看出,与GWO、SOA和基本GJO算法相比,I-GJO具有更快的收敛速度。

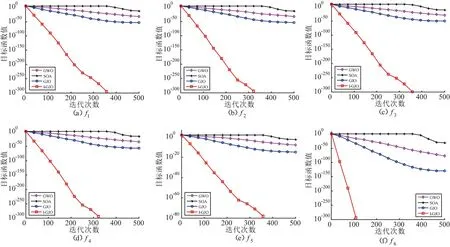
图5 4种算法对6个问题的收敛曲线

4 基于I-GJO算法的特征选择

特征选择是一种常用的高维数据降维方法。构建合适的目标函数,特征选择可转化为求解一个函数优化问题,其目标函数可表述为:

fobj=(1-ρ)·Acc+ρ·|l|/|L|,

(11)

式中:ρ为权重,Acc表示分类精度,|l|为所选择的特征数,|L|表示数据集的原始特征数。

本节应用I-GJO算法解决特征选择问题,以进一步测试它的优化性能。从UCI数据库中选取16个常用的数据集进行实验,数据集的详细信息见表3。

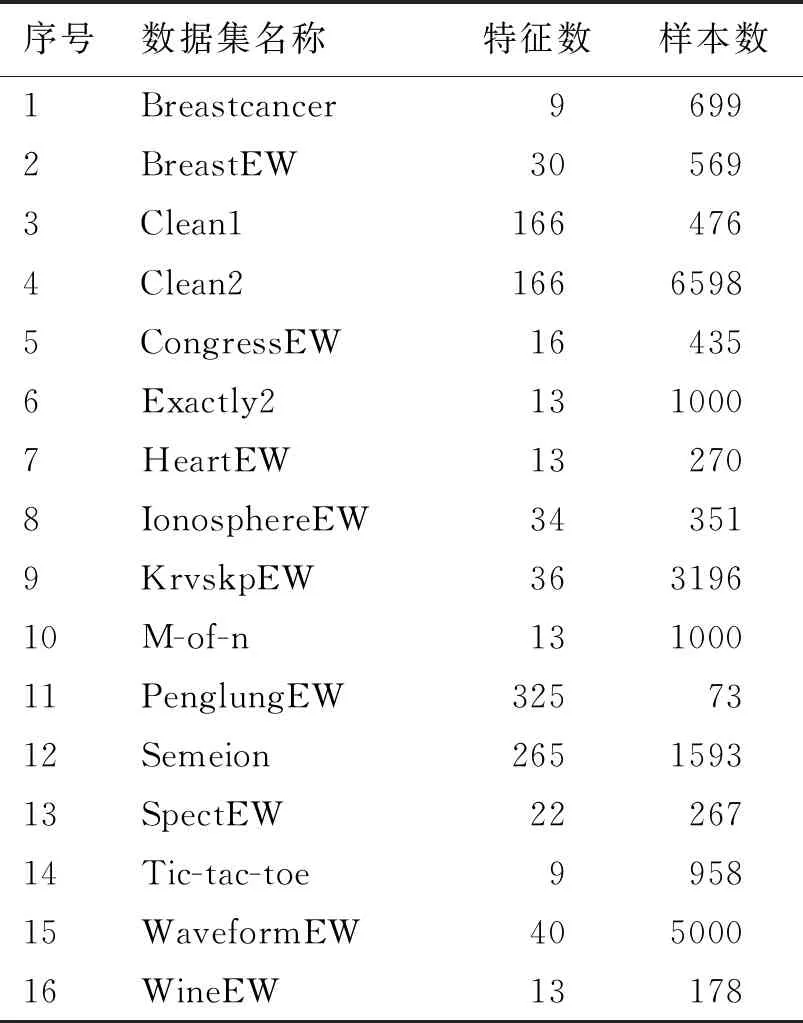
表3 16个UCI数据集

GWO、SOA、GJO、I-GJO算法对表3中的16个数据集进行特征选择,结合包裹式方法和k-近邻(KNN)模型进行分类。在实验中,将每个数据集样本随机分为训练集(80%)和测试集(20%)。4种算法的种群大小为30,最大迭代次数为10,k=3,ρ=0.01,对每个数据集单独运行10次,获得的平均分类精度和平均所选择的特征数分别见表4和表5。

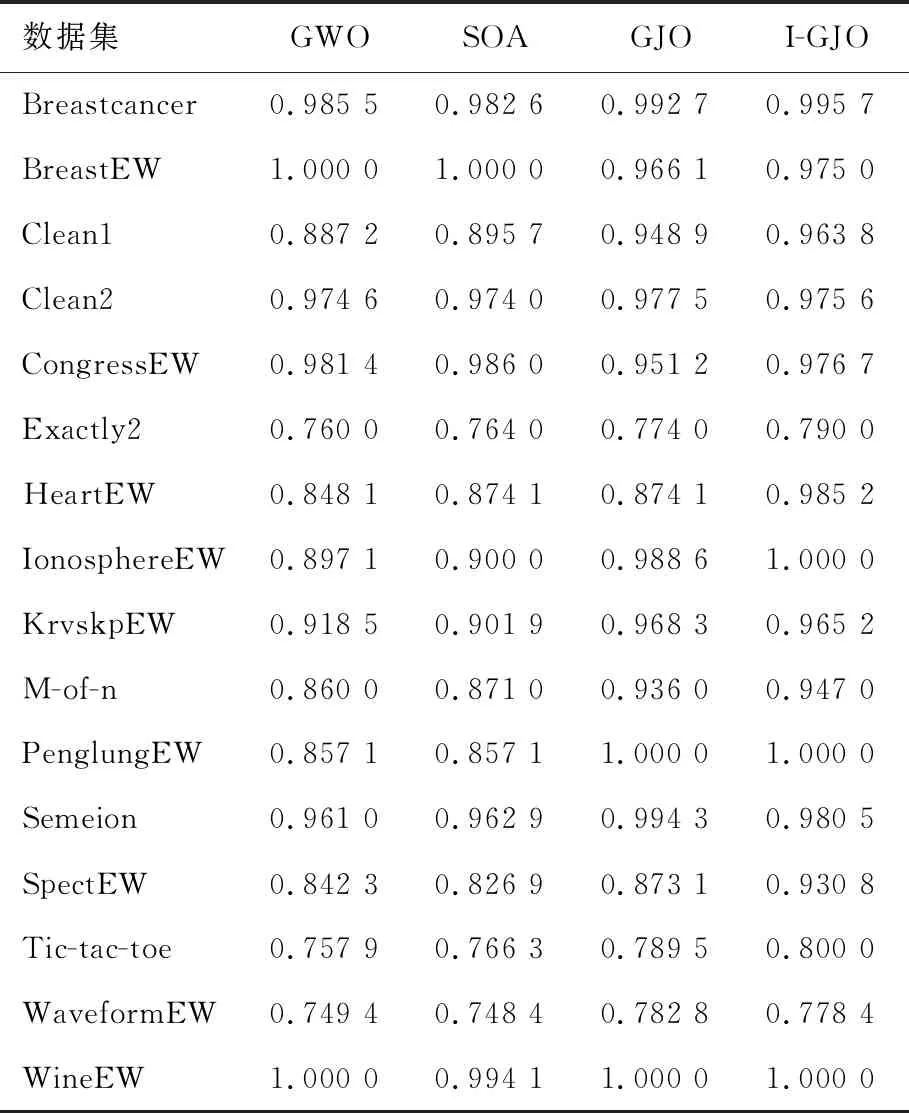
表4 16个UCI数据集的平均分类精度

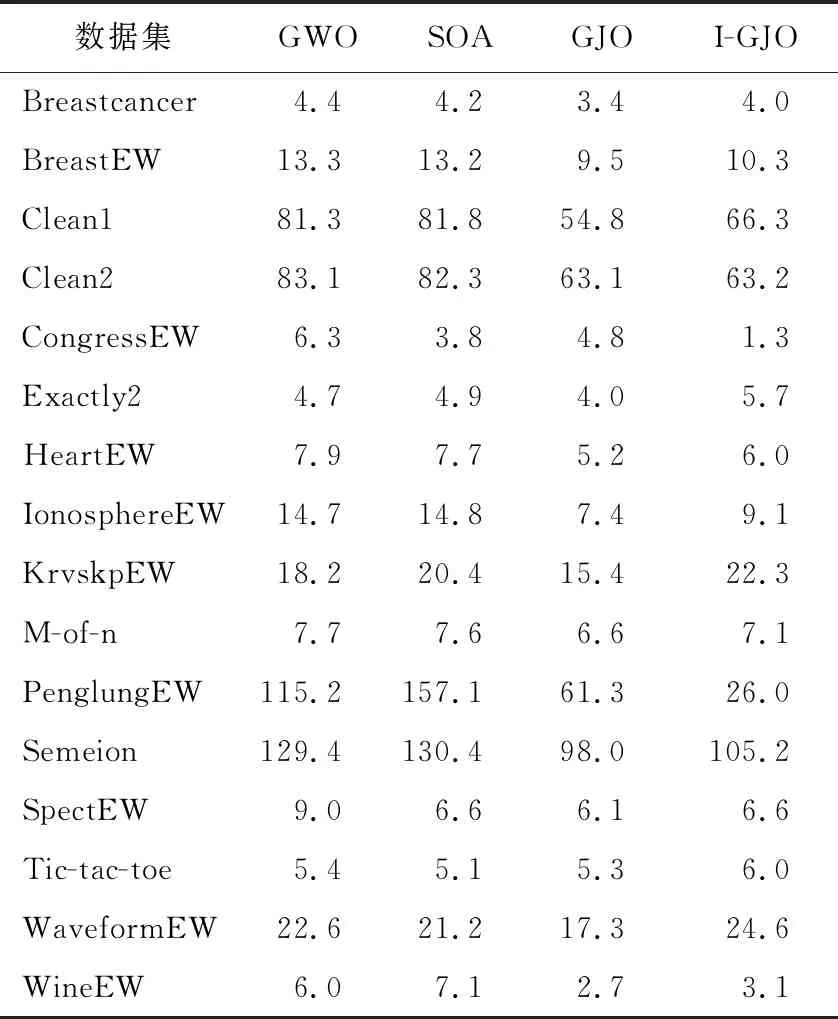
表5 16个UCI数据集的平均所选特征数

从表4中可以看出,I-GJO在12个数据集上获得了比GWO算法更好的结果;对于数据集WineEW,两种算法得到了相似的分类精度;而GWO算法在BreastEW和CongressEW数据集上取得了更优的结果。与SOA相比,I-GJO算法在13个数据集上获得了较高的分类精度;但是,SOA在数据集BreastEW和CongressEW上得到更好的结果。I-GJO在10个数据集上获得的平均分类精度比GJO算法要高;然而,GJO在Clean2、KrvskpEW、Semeion和WaveformEW数据集上取得了更优的结果;对于PenglungEW和WineEW,两种算法的性能相似。由表5可知,与GWO和SOA相比,I-GJO算法在大部分数据集上所选择的特征数要少;然而,与GJO算法相比,I-GJO在大多数数据集上所选择的特征数要稍多。以上实验结果表明,I-GJO算法是一种可行的特征选择方法。

5 结束语

为了提高基本GJO算法在求解函数优化和特征选择问题的性能,设计了一种改进GJO算法。首先,分析了猎物逃脱能量E在算法搜索过程中平衡探索和开发能力不足的问题,在此基础上提出了一种新的非线性递减逃脱能量公式;其次,在算法迭代后期引入翻筋斗学习策略以增强群体多样性,从而降低算法出现早熟收敛的概率。设计两个实验用于测试I-GJO算法的可行性,首先选取6个基准函数优化问题进行数值实验,结果表明,与GWO、SOA和GJO算法相比,I-GJO在6个函数优化问题上均得到更高的收敛精度和更快的收敛速度。然后利用I-GJO解决包含16个数据集的特征选择问题,仿真结果显示改进算法能有效选择最优特征,从而达到提高分类精度的目的。

下一步研究是将改进算法用于求解其他类型优化问题如约束优化、多目标优化、动态优化等,以及一些实际应用问题。