基于数字孪生机床模型的加工路径优化研究
2024-02-03蔡杨
蔡 杨
(浙江永成机械有限公司, 浙江绍兴 311835)
0 引言
数字孪生技术可以实现在虚拟空间实时映射物理实体状态,在智慧城市建设中发挥着不可替代的作用[1]。 在加工领域,数字孪生技术的应用也开始受到大力关注,通过数字孪生技术实现对加工过程的数字孪生建模, 通过加工信息的虚实交互,实现对加工过程的全流程监测,并用于辅助加工[2]。 目前,加工领域的数字孪生模型大多为固定工况建模,而随着制造业个性化需求愈发强烈,要求加工过程需要根据生产要求对工况进行动态调整, 而固定工况建模无法实现加工路径的自适应优化[3]。 鉴于此,本研究提出了基于数字孪生机床模型的加工路径优化策略,以解决动态数控加工问题。
1 数字孪生机床模型的构建
数字孪生是对目标物理实体全生命周期的虚拟映射描述,数字孪生模型的实质为物理实体的结构特征、运行机理与响应特性的数字化表达[4]。数控机床是制造业非常重要的加工设备,将数字孪生技术应用到数控机床中,可以构建以数控机床为目标物理实体的数字孪生机床模型[5]。 该模型构建涉及不同子系统模型与虚拟映射策略, 具体如图1 所示。

图1 数字孪生机床模型
本研究构建数字孪生机床模型的目的在于为后续实现加工路径优化奠定基础, 采用虚拟映射策略实现对各类加工设备的实时信息采集, 并上传至三个子系统模型中,实现不同子系统模型与物理实体间的实时虚实映射,具体流程如下:
(1)分解目标系统,根据实际加工需求,将数字孪生机床模型分解为3 个子系统模型。
(2)细分子系统,根据物理实体的功能部件组成,对子系统进行功能部件的划分,以确定关键运行信息。
(3)机理分析,根据不同子系统的运行特征,对三个子系统进行功能部件的机理分析。
(4)Modelica 编译,根据运行机理,对各子系统功能部门进行编译与描述, 形成用于构成子系统模型的功能元件。
(5)模型构建,分析不同子系统之间的耦合关系,搭建耦合接口, 从而实现不同子系统在整个模型中的耦合连接,完成最终建模。
2 基于数字孪生机床模型的加工路径优化
2.1 加工路径优化问题描述
加工路径优化问题属于典型的NP 问题,其实质为计算零件加工的最短加工路径。通过对工件信息的解析,可以获取到工件基元数量、工件分布状态、工件位置等加工基元特征,其集合表示为:
式中:n—目标加工基元的种类数;ai—第i 种加工基元对应的具体加工信息, 其由每个加工基元的基本属性信息构成:
式中:Ra—第i 种加工基元的尺寸信息;N—同种特征加工基元数;Ti—加工基元所采用的刀具信息;jk—加工基元采用的加工方法。
采用数组形式进行所有加工基元抽象点坐标的储存,从而获取到向量P=(P1,P2,…,Pn),Pi为第i 种加工基元的抽象点坐标集合,表示如下:
式中:Pi,j为第i 种加工基元第j 个基元的抽象点坐标,Pi,0、Pi,N+1分别表示刀具起始位置与刀具终止位置。
为保证获取到最优加工路径,构建约束条件,分别为数控加工运动干涉约束、重复走刀约束、基元加工顺序约束、刀具寿命约束,具体如下:
式中:g0—基元零部件与刀具间的最大间隙值;pi,k—刀位点坐标;T—全部刀具集合,T=(T1,T2, …,Tm);O—采用同一种刀具加工同一类加工基元时的工艺顺序约束,O=(O1,O2,…,On);j—加工方式约束;Tt—刀具寿命。
其中, 数控加工运动干涉约束设定为基元零部件与道具间的间隙值应小于允许的最大的间隙值; 重复走刀约束设定为同一基元在同类同工序的路径优化中仅会出现一次; 基元加工顺序约束设定为基元加工顺序需要满足工件加工的具体要求以及相关工艺约束条件, 需要注意的是OI的表现形式为加工顺序约束矩阵, 具体可见式(5);刀具寿命约束设定有两种,分别为刀具寿命大于基元总加工时间,以及刀具寿命小于基元总加工时间,两种情况下OI分别为k2与0。
在设定约束条件的基础上, 进一步对函数目标进行优化,优化目标考虑到走刀长度与换刀成本。 在实际加工中, 加工行程的构成包括实际加工轨迹与基元间移动行程,可以根据实际加工工艺参数而获取到实际加工轨迹,而基元间移动行程则由控制方式而决定, 由此可构建出走刀长度的计算表达式, 通常表征为两个加工基元间的欧式距离与基元加工时刀具的走刀轨迹。 而到完成一类基元加工以后,通常需要换刀,这一环节会耽误一定的加工时间,且需要在换刀点与基元间不断移动,同样会增加走刀长度,因此形成了换刀成本,换刀成本目标函数的构成则应包括换刀时间与换刀所增加的走刀长度两个部分,通常表征为两个基元与换刀点间的欧式距离。 加工路径优化目标函数需要同时考虑到走刀长度函数与换刀成本函数,且两者的比重具有一定差异性,需要采用加权系数法将两个子目标函数转换为单目标函数, 则最终可获取到的加工路径优化问题描述模型如下:
2.2 求解算法设计
本研究采用IGASA 算法进行加工路径优化问题的求解,具体流程如下:
(1)编码与解码,首先,对目标加工零件特征进行解析,并转化为多段路径优化问题,在模型中输入好数控基点原点位置,以及根据加工工艺分析得到的换刀位置,并完成基元加工位置的编码以及将最优染色体转化为加工路径信息。
(2)初始化种群,通过随机生成函数获取到初始种群S0,并采用改良圈算法进行改良,以获取到更优的初始种群S1。
(3)初始化参数,包括初始温度T0、结束温度Te、温度衰减因子、进化次数ng、最大迭代次数ng-max、交叉概率pc、变异概率pv、当前解Ec、当前路线sc、最优解Eb、最优路线Sb。
(4)计算个体适应度f(x),个体适应度用于评价染色体的优劣,本研究中定义适应度函数为加工行程倒数,该值越大,说明优化函数值越小。
(5)精英保留与改进轮盘赌,采用精英保留的方式获取到个体适应度值最大的染色体, 并采用改进轮盘赌选择其余染色体,以进一步提高个体累计概率。
(6)交叉,首先,在需要交叉的两组染色体的父代染色体中随机选取任意相同位置的基因;其次,生成两组长度为n 的子代染色体, 且对应位置基因与选取的父代染色体基因相一致;然后,确定最初选择的基因在另一组父代染色体的位置, 并将其余基因依次填入到子代染色体中;最后,计算新产生的个体适应度值,根据该值与原适应度值的大小对比决定该个体的采纳方式。
(7)变异,针对种群内的任何一个个体,随机生成0到1 之间的伪随机数,将该值与变异概率pv 进行对比,若该值大于pv, 则将染色体基因片段进行反转, 生成新个体,并根据Metropolis 准则判断是否需要采纳。
(8)种群改良,采用改良圈算法改进种群,获取到个体适应度值更高的种群。
(9)判断循环是否终止,对于两种循环方式:GA 种群迭代循环当满足最大迭代次数后将终止循环,否则进入下一次循环;SA 降温循环当大于结束温度时将终止循环,否则重新搜索。
2.3 加工路径动态优化
将上述算法嵌入到数字孪生机床模型中,以数字孪生机床模型进行实时数据更新, 从而可以保证上述算法的准确性。 数字孪生机床模型在实际加工中将实时监测加工工艺参数与数控机床运行参数, 一旦感知到运动误差与刀具寿命等数据发生转变以后, 则重新对上述模型中的约束条件进行判断并更新,且当约束条件更新时,模型将会自动进行算法参数的更新,从而采用IGASA 算法重新计算最优加工路径。 基于数字孪生机床模型的加工路径优化是一种数字孪生虚实共同演进的过程, 首先采用IGASA 算法获取到原始加工路径, 数字孪生机床模型通过语义模型将原始加工方案转换为代码形式, 上传至数控系统,并按照原始加工方案进行数控加工。 同时,数控机床的各类传感系统将不断获取各类参数数据, 并反馈至数字孪生机床模型, 该模型根据获取到的实时参数数据进行数控加工的监控与仿真, 判断当前加工路径是否合理, 若不合理则对应进行优化调整, 实现物理空间及其孪生体的同时演进, 并构成闭环式路径优化方案, 具体流程图如图2 所示。
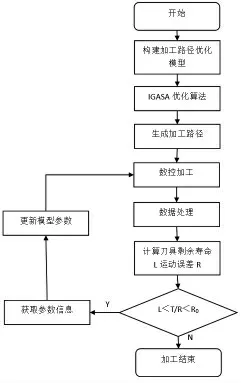
图2 加工路径动态优化流程
3 效果验证
为了验证上述方法的有效性, 以箱体零件加工进行验证,获取到的箱体零件特征如表1 所示。

表1 箱体零件特征

表2 加工方案对比

4 结束语
本研究根据数控机床的加工特征, 提出了通过数字孪生技术构建数字孪生机床模型, 实现虚实融合的数控机床控制方案,并针对数控机床加工路径设计问题,提出了将IGASA 算法嵌入到数字孪生机床模型中, 通过IGASA 算法寻找到加工路径的最优解,以解决数控机床加工路径设计问题。
