纳秒脉冲激光降低超声速流场波阻机理研究

2024-02-03卿泽旭王殿恺

机电产品开发与创新 2024年1期

江鹏，卿泽旭，王殿恺*

（1.北京特种工程设计研究院，北京 100028； 2.航天工程大学激光推进及其应用国家重点实验室，北京 101416）

0 引言

减小超声速飞行器波阻可以显著提高气动性能，节省燃料，增加航程。主动流动控制是在流场中注入能量从而改变流场原有特性的手段，控制对象包括阻力、热载、边界层分离和转捩以及燃烧等，是目前国际研究热点。美国发起了高度可重复性太空运输计划，为了提高飞行器在爬升段的性能，防止飞行器在再入段的烧蚀，开发了电磁减阻系统[1]；日本在国家超声速运输实验项目中包括了减小超声速飞行器波阻的研究[2]；俄罗斯AJAX 项目和欧洲The EUROSUP 计划中也包括了能量沉积减小波阻的研究内容[3-4]。减小波阻的可行方法包括在飞行器前方安装锥状物体、从飞行器前段逆向喷流以及在飞行器前方流场沉积能量（电弧放电[5-8]、激光[9-11]、微波[12-14]等）。安装在飞行器前方的锥状物体具有较高的减阻效率，但存在热蚀现象，且对飞行控制带来一定挑战；逆向喷流结构复杂，且对飞行器结构有一定影响；电弧放电比较容易实现，但也存在电极烧蚀和影响气动外形等问题。激光能量沉积减阻是向弓形激波的上游沉积激光能量，聚焦击穿气体改变流场以减小波阻。激光能量沉积具有方向性好、可控性好、可机载和不影响气动外形的特点，有良好的应用前景。脉冲激光更易于击穿空气，实现能量沉积，相比于连续能量沉积具有较高的能量效率[15-16]。

本文采用纳秒脉冲激光能量沉积的方法减小超声速飞行器波阻，研究高重复频率的纳秒脉冲激光与超声速流场的相互作用机理，阐明阻力减小的基本原理，为工程应用奠定良好基础。

1 数值模拟方法

1.1 计算模型

目前，大多数学者都认为在激光能量沉积结束的时刻，等离子体热核已经处于局部热力学平衡状态。相关的实验研究表明，热核在脉冲结束的1ns 内就已经到达局部热力学平衡状态。而激光能量沉积减阻研究均在激光脉冲结束后的微秒量级。在激光能量沉积后，空气增加的热力学内能包括平动能、转动能、振动能和电子势能，需要用平动温度、转动温度、振动温度和电子温度来描述。而采用局部热力学假设之后，可以只用一个温度来描述等离子体热核的状态，从而大大简化了能量方程的数目。

在局部热力学平衡的基础上，对激光能量沉积后热核演化过程进行简化：①轴对称、非定常、可压缩的层流流动；②激光脉冲结束时空气各组分的速度为0m/s；③不考虑空气的热力学非平衡效应、电磁效应和热辐射的影响；④热核中各组分的浓度和物性参数只与温度有关；⑤满足理想气体状态方程。

Dors 在研究激光能量在静止空气中沉积时采用了非对称泪滴形能量沉积模型[17]。该模型认为热核的初始形状并不是球形或椭球形，而是泪滴形。模型的核心假设是：温度在激光入射轴上的为指数衰减，而垂直于激光入射轴上为高斯分布。本文借鉴Dors 的能量沉积模型，提出针对波长1064nm、脉宽10ns、单脉冲激光入射能量39.9mJ（沉积能量约10.6mJ）的能量沉积模型。 300～20000K 范围内空气等离子体的物性参数，包括比热容、粘度、导热系数、相对分子质量和声速等，均可认为是温度的函数[18]。

1.2 计算方法

在用Fluent 软件进行计算之前，需要把温度数据拟合为多项式函数的形式，然后通过UDF 导入Fluent 计算过程。针对环境温度和压力分别为283K 和101325Pa 的激光诱导氧气火花的演化过程，基于采用二维轴对称假设，取15mm×30mm 的二维矩形作为计算区域。经验证，30 网格/mm 就可以满足网格无关性条件。

对于高重频激光能量沉积对钝头体的减阻机理研究，先计算得出未受扰动的超声速流场，然后根据频率计算出每个脉冲的间隔时间，再利FLUENT 软件的UDF 按照间隔时间逐个实现单脉冲激光能量沉积，从而达到高重频能量沉积的目的。通过研究流场的波系结构和压力分布来揭示减阻机理。所采用的计算网格和边界条件如图1 所示。

图1 边界条件和网格划分

来流的方向为由左至右，设置为压力远场边界。右侧设置为压力出口，x 轴上为axis 边界，圆柱形钝头体表面为无滑移壁面边界。采用C 型网格，在axis 边界均匀布置900 个网格；压力出口边界作为与其相对应的边，同样设置900 网格，并且在靠近钝头体的一端进行了加密处理。钝头体圆柱的高取为0.01m。圆柱底面的半径和高分别均匀布置300网格；压力远场边界作为与二者相对应的边，设置为600网格，且在两端加密。这样设置可以保证热核与钝头体流场相互影响区域的网格密度达到30 网格/mm，满足网格无关性条件。采用基于密度的非定常求解器，选择隐式AUSM 的通量差分格式，空间离散选择Green-Gauss Cell Based 方式的二阶迎风格式。

计算条件为：气流Ma=1.92，冲击直径20mm 的圆柱形钝头体。在圆柱形钝头体上游40mm（l/d=2.0）处沉积重复频率为80kHz 的纳秒脉冲激光能量，沉积的激光能量为0.8mJ。如表1 所示。

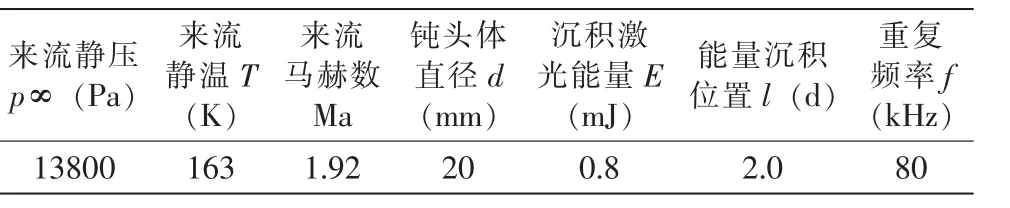
表1 高重频激光能量沉积计算参数

1.3 计算模型与方法的验证

在无激光能量沉积时，计算得到的基准波阻DB为21.1N，Sasoh 实验[19]测得基准波阻为22.4±0.3N，误差5.8%。相比于Sasoh 的无粘、不考虑真实气体效应的数值结果20.6N（误差8.0%），本文钝头体基准波阻的计算更准确。本文计算得到激波脱体距离为9.2mm，实验值为9.0mm，误差2.2%。同时，钝头体左端面边缘处的膨胀波以及由边缘延伸出的滑移层也与实验相当吻合，如图2 所示。基准波阻、激波脱体距离、膨胀波以及滑移层的计算结果验证了上述数值方法的可靠性。

图2 无激光能量沉积时密度梯度云图与流场纹影照片对比

2 减阻机理分析

图3 给出了本文计算得到的典型流场密度梯度云图，并与Sasoh 的实验结果进行了对比。

图3 80kHz 激光能量沉积的典型流场纹影图和本文密度梯度云图计算结果

从密度梯度云图可知，每一个激光脉冲形成的热核在经历钝头体前的激波后均演变为了涡环结构。涡环在靠近钝头体的过程中，不断在其径向拉伸。诸多涡环在空间上叠成了一个锥形结构，覆盖在钝头体前方。弓形激波变形为从锥形涡环结构顶端延伸出来的斜激波。图3 中还能清晰地观察到再压缩过程的压缩波（XIII）。压缩波在锥形涡环结构内部仍存在，但是被锥形涡环结构打断。计算得到的流场拓扑结构与实验相当吻合。

钝头体波阻变化曲线如图4 所示。

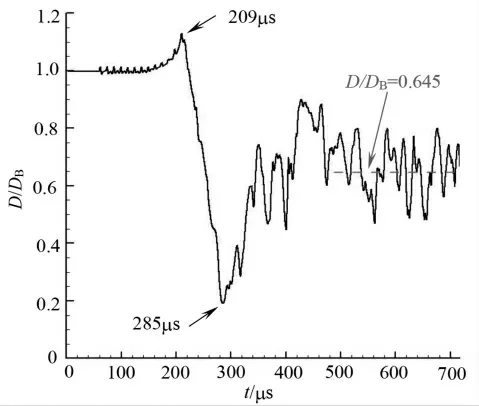
图4 80kHz 激光能量沉积时钝头体归一化波阻变化曲线

图中波阻由钝头体表面压力积分而得，波阻已经进行了归一化处理。t=0μs 时，高重频激光能量开始沉积到流场中。t=209μs，波阻达到最大值，约为DB 的112.4%；此后波阻逐渐下降，在t=285μs 时，达到最小值，约为DB 的19.2%；此后波阻开始回升，大约在t=450μs 后逐渐趋于稳定，约为DB 的64.5%。

对高重频激光能量沉积作用下的波阻曲线变化进行解释。波阻在t=209μs 之前出现小幅波动，这是由激光能量沉积诱导冲击波所导致的。由于激光能量沉积位置离钝头体较远，冲击波衰减程度比较大，因此波阻受冲击波的影响较小。 t=209μs 时波阻曲线出现峰值。这是因为热核演化形成的涡环在不断靠近钝头体左端面的过程中，使钝头体左端面产生了漩涡，如图5 中的XIV。该漩涡使得原本应当流过钝头体左端面的流体运动方向有所改变，流体不再向下游运动而是向上游流动，以致于在钝头体左端附近形成一道激波（图5 中的XV）。

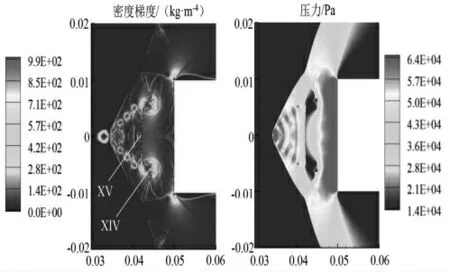
图5 t=209μs 时流场的密度梯度云图和压力云图

钝头体左端面的边缘处流体有所阻滞，而原本钝头体左端面的中心驻点处流体得以逆流而上，离开钝头体，因此钝头体左端面中心处的压力较无能量沉积时要小，而边缘处的压力较无能量沉积时要大，这点从图中t=209μs 和t=0μs 时的钝头体左端面压力分布对比也可分析得到。左端面压力变化的总效果使得波阻增大为DB 的112.4%。

随着上面分析到的漩涡不断流向下游并最终离开钝头体左端面，左端面的高压气体不再受到漩涡的约束而得以释放，表现为左端面的压力骤降，如图6 和图7 中t=285μs 的曲线，从而波阻曲线在t=285μs 时出现谷值。

图6 t=285μs 时流场的密度梯度云图和压力云图

图7 不同时刻的钝头体左端面压力分布对比

在t=285μs 之后，波阻回升并在DB 的64.5%附近不规则振荡，这是由于锥形涡环结构的周期性变化与再透射-反射波系周期性冲击钝头体相耦合的结果。

计算得到的压力分布与无能量沉积时的压力分布对比如图8 所示。无能量沉积时，弓形激波的波后是一片高压区，完整覆盖了整个钝头体左端面。而在80kHz 激光能量沉积时，弓形激波已变形为斜激波，波后压力普遍下降。特别是在涡环所在的位置，压力最低。只有少数压力较高的区域，这是由再压缩过程导致的。压缩波被涡环打断，从而形成两部分。一部分压缩波在锥形涡环结构之外，强度较单脉冲激光能量沉积时的压缩波明显变弱；在锥形涡环结构内部的压缩波，相比单脉冲激光能量沉积时强度稍弱，但压缩波的范围大大减小。