雷达鸟类目标微多普勒贝叶斯增强算法
2024-01-30孙卫天毛欣瑶夏亚波桑婧隺
杨 磊, 孙卫天, 毛欣瑶, 夏亚波, 桑婧隺
(1. 中国民航大学电子信息与自动化学院, 天津 300300;2. 天津港远航国际矿石码头有限公司, 天津 300452)
0 引 言
近年来,鸟类入侵事件频繁在机场净空保护区发生,如2009年全美航空一架代号为1549的航班在起飞不久后就撞上一群加拿大黑雁,使得两个引擎都失去了推力而不得不滑翔飞入哈德森河;2020年5月9日,CA908航班因为其发动机叶片遭遇鸟击而被迫返航。类似鸟击事件不断上演,给飞行安全带来了极大威胁。因此,实现机场附近鸟群可靠探测与监视对避免鸟群威胁航空飞行安全具有十分重要的意义[1]。
雷达由于具有全天候、全天时、远距离探测等优势,被广泛运用于探测鸟类等非合作目标场合[2]。目前相对成熟的探鸟雷达系统有美国DeTect公司开发的MERLIN(梅兰)系列、加拿大Sicom System公司开发的Accipiter(苍鹰)系列以及荷兰TNO公司开发的ROBIN(罗宾)系列[3]。MERLIN系列天线扫描区域广,效率高,但无法获得三维信息;Accipiter系列能够获得鸟类目标的三维信息,但其天线扫描区域有限,效率较低;ROBIN系列具有低成本、高精度、能够对信号和图像进行一体化处理、可同时跟踪上万鸟类的优点,但是其在海杂波滤除等方面的测试尚在进行中。鸟类目标的雷达回波强度受限于两个因素:一是鸟类目标具有比较小的雷达散射截面(radar cross section, RCS),二是机场近场强杂波的影响。因此,利用传统恒虚警率(constant false-alarm rate, CFAR)方法进行鸟类目标探测会比较困难。此外,鸟类目标是非合作目标,其机动性较强,难以实现较高的积累响应,因此有必要研究针对鸟类目标的有效探测方法。
对于鸟类目标,其飞行时翅膀规律性的扑翼运动会在由主体平动产生的雷达多普勒频移回波信号附近引入额外调制边带,即微多普勒效应。而微多普勒效应反映了多普勒频移瞬时特性,表征了目标微动的瞬时径向速度。同时,利用微多普勒信号可以反演出目标运动特性,例如翼型、姿态等信息。因此,尽管鸟类目标雷达回波强度较弱,但可以利用其中微多普勒效应对其进行有效的探测和识别[4-5]。
由于鸟类目标微多普勒效应随时间变化,而传统傅里叶变换不能描述任一时刻的信号频率成分,无法对其进行全面分析。为了解微多普勒效应随时间变化的关系,需要使用时频分析方法,将时域一维信号映射到时频二维平面,全面反映非平稳信号时频联合特征。常见的时频分析方法分为两种,即非线性时频分析方法和线性时频分析方法[6]。其中,非线性时频分析方法有维格纳-威尔分布(Wigner-Ville distribution, WVD)、伪维格纳-威尔分布(pseudo Wigner-Ville distribution, PWVD)、平滑伪维格纳-威尔分布(smoothed pseudo Wigner-Ville distribution, SPWVD)、希尔伯特黄变换(Hilbert-Huang transform, HHT)。WVD将信号能量分布于时频二维平面内,其时间带宽积达到了测不准原理下界,但是由于WVD是双线性变换,因此会产生交叉项,使得时频分布受到干扰且抑制了二次型时频分布的推广。PWVD是对WVD进行加窗处理,使得WVD的完全非局部性变为局部化,在一定程度上抑制了多分量信号的交叉项。SPWVD是WVD与平滑函数进行卷积的结果,可以较好地消除交叉项,但其运算复杂。HHT是一种自适应方法,可通过信号经验模态分解,使非平稳信号平稳化,但其存在边界效应。无论是哪种非线性时频分析方法,交叉项的产生或运算的高复杂度,均不利于后续信号处理和特征增强,因此本文采用线性时频分析方法。
在线性时频分析方法中,线性时频分析方法有短时傅里叶变换(short-time Fourier transform, STFT)、小波变换(wavelet transform, WT)以及拉普拉斯变换(Laplace transform, S)。STFT需要在时域对信号进行加窗处理,这意味着STFT无法同时达到高时间分辨率与高频率分辨率,即当窗函数变窄时,时间分辨率高而频率分辨率低;当窗函数变宽时,时间分辨率低而频率分辨率高。WT对时频二维平面是一种机械式的划分,且所获结果不一定是真正的时频谱。S变换相对于STFT运算较为复杂。因此有必要研究在时频域上对微多普勒特征进行特征增强的方法。
由于鸟类目标微多普勒特征在时频二维平面呈现出明显的稀疏性,根据压缩感知(compressed sensing, CS)理论可知,能够利用特征增强的方法恢复微多普勒特征[7]。基于CS进行特征增强的方法主要包括贪婪类算法、凸优化类算法和贝叶斯类算法[8-9]。贪婪类算法通过迭代搜索均方根误差最小的局部稀疏得到最优解,并在解的稀疏度小于某一经验值时停止迭代[10-11]。常见的贪婪类算法有匹配追踪(matching pursuit, MP)算法、正交匹配追踪(orthogonal matching pursuit, OMP)算法等。虽然OMP算法运算效率快,但其稀疏度需预先自行设定,这使得稀疏度无法自适应地满足实际目标特征的需求,难以适应现实先验特征建模的需要,导致特征恢复精度有限。凸优化类算法通过最小化目标的1范数并结合基追踪抑噪进行稀疏恢复[12-14],例如凸优化算法,其基于不断优化设计最终得到最优解,但在高维数据情况下,凸优化算法运行性能低,耗费时间长。贝叶斯类算法通过引入目标特征先验分布,利用分层模型进行推理,进而得到后验概率密度函数估计[15-18],常见算法如稀疏贝叶斯学习(sparse Bayesian learning, SBL),其对目标特征以先验概率表征,通过分层可以保证获得解析解,求解精度高且无需多次独立同分布实验,仅需单次测量结果即可。通常,先验分布选择拉普拉斯分布、高斯分布。拉普拉斯先验在降采样、低信噪比情况下会造成求解过稀疏,即目标特征恢复结果损失一部分连续性。高斯先验抑制噪声能力不强,会造成目标特征恢复结果过于平滑。
针对以上问题,本文提出利用广义高斯分布(generalized Gaussian distribution, GGD)在时频域对鸟类目标微多普勒特征进行先验自适应建模。该分布可以根据不同场景,灵活选择先验模型,从而避免了目标特征恢复结果因过于稀疏而丢失连续性、因过于平滑而保留过多噪声的问题。然而,GGD先验与所假设的高斯似然函数由于不共轭而无法得到闭合解。针对该问题,本文利用贝叶斯分层模型对鸟类目标微多普勒特征及相关参数进行层级建模推理,并建立参数依赖的后验分布。考虑到动态可变GGD先验造成目标特征后验分布非平滑、求解运算效率低等困难,本文在可以快速高效求解后验分布的未调整朗之万算法(unadjusted Langevin algorithm, ULA)基础上引入了近端算子,以高效求解目标特征非平滑后验分布的解析解。最后,通过模拟强杂波噪声等现实场景,将本文所提贝叶斯增强算法与STFT算法、凸优化算法特征恢复结果作对比,分析了本文所提贝叶斯增强算法在微多普勒特征增强方面的优势,并利用实测数据验证了该贝叶斯增强算法的有效性。
1 微动目标信号模型
自然界中,鸟类的飞行模式主要有两种,一种是鸟类达到一定高度或速度后,伸开双翅不动在空中滑行前进。此飞行模式称为滑翔,多见于高空。另一种是扑翼飞行,这是所有鸟类最常见、最基本的飞行模式。鸟类在近地面以及低空飞行时大多采用该飞行模式。此时,鸟类飞行高度正好与起飞或者降落的飞行器所处高度重合,常常容易引发鸟击事件。因此,研究鸟类低空扑翼飞行模式对于避免鸟类撞击飞行器是十分有必要的。鉴于鸟类飞行时翅膀规律性扑翼运动是产生微多普勒效应的主要原因,下面将研究鸟类扑翼时的微动信号模型。
1.1 鸟类目标扑翼模型
鸟类翅膀结构如图1(a)所示,若类比并借用人体手臂术语,鸟类翅膀包括了翼弦、半翼展、上臂、前臂以及手,能够完成扑翼、扫翼及扭翼等运动形式。扑翼是指上臂或翼弦围绕某一个关节以一定扑翼角度做上下运动。扫翼是指肩部做前向延伸或后向回收运动。扭翼是指翅膀围绕鸟自身主轴做旋转运动,该运动可以引发翅膀前缘下降以及后缘上升。接下来,主要侧重分析鸟类的扑翼运动。

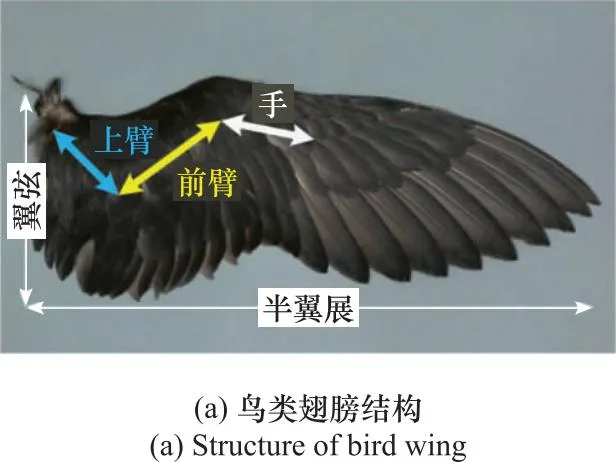
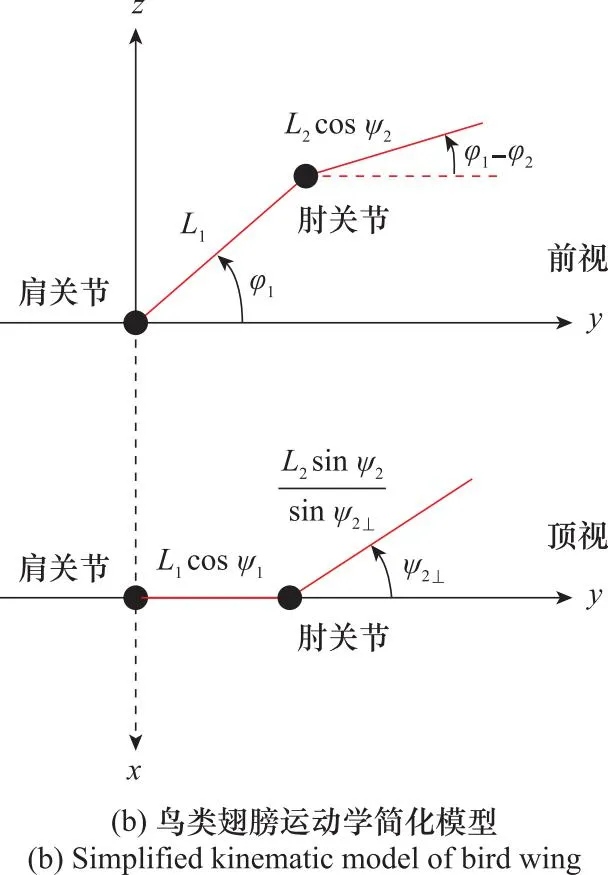
图1 鸟类翅膀结构及运动学简化模型Fig.1 Structure and simplified kinematic model of bird wing
在以上假设基础上,上臂扑打角度的调和时变函数为
φ1(t)=A1cos(2πfflapt)+φ10
(1)
前臂扑打角度的调和时变函数为
φ2(t)=A2cos(2πfflapt)+φ20
(2)
前臂扭转角度的调和时变函数为

(3)
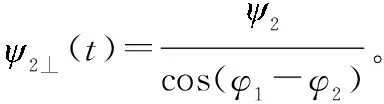
(4)
鸟翼型肘关节位置为
(5)
综上,借用鸟类翅膀运动学简化模型,便可产生鸟类目标扑翼模型的雷达回波信号。
1.2 鸟类目标微多普勒模型
忽略鸟身宽度且假设鸟类翅膀在运动过程中翼面不弯曲,建立如图2所示的空间坐标系。具体地,以雷达S为原点建立坐标系(X,Y,Z)和以鸟两侧翅膀根部连线中点O(以下称为对称中心)为原点建立鸟类目标扑翼坐标系(x,y,z),其中y轴方向为鸟首方向。雷达坐标系与鸟类目标扑翼坐标系平行。雷达S到O点的距离为R0,方位角为α,俯仰角为ϑ。为简便计算,假定鸟类目标以扑翼频率Fbird沿y轴正半轴飞行,其翅膀上任意点的移动可以认为是平飞和翅膀扑翼两种运动的合成。若平飞速度为v,扑翼角度φ(即翼面与xoy平面的夹角)为随时间变化的函数,即
φ(t)=θmaxsin(2πFbirdt+φ0)=θmaxsin(ω0t+φ0)
(6)
式中:θmax为扑翼角度幅值,即翼面与xoy平面的最大夹角;ω0=2πFbird为扑翼角频率;φ0表示初始时刻鸟类目标扑翼角度相位。为简化分析,令φ0=0。
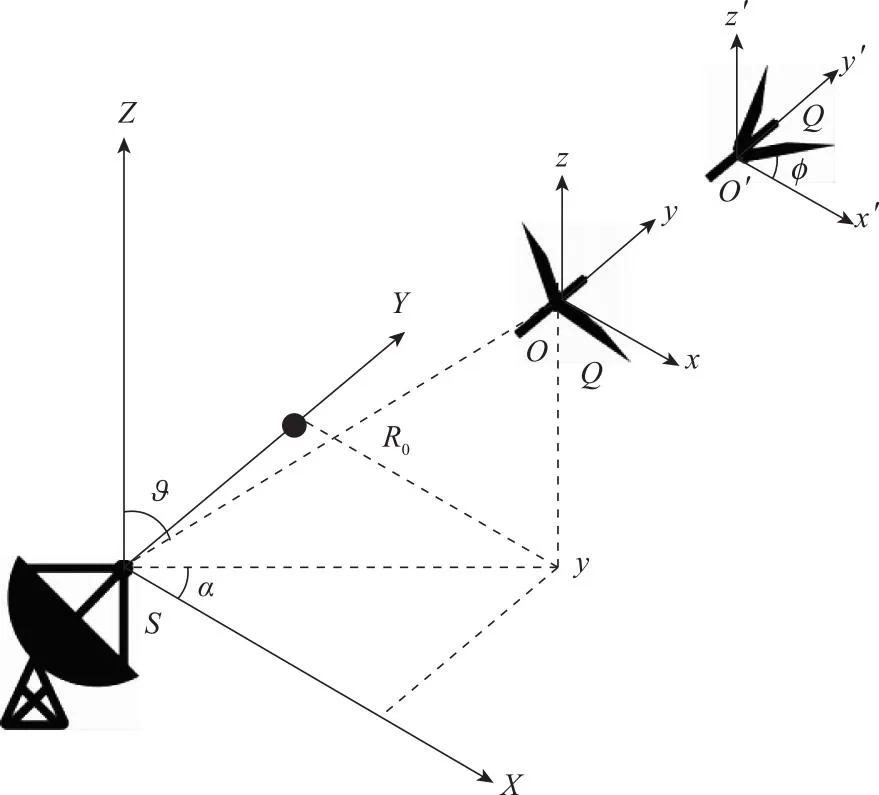
图2 雷达与鸟类目标几何关系图Fig.2 Geometric relationship diagram of radar and bird target

R(t)=|R0+OO′+O′Q|2=
{(R0sin ϑcosα+lcos[φ(t)])2+(R0sin ϑsinα+vt)2+
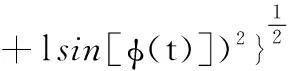
(7)
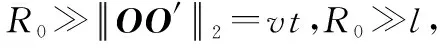
R(t)≈R0+vtsin ϑsinα+
lcosαsin ϑcos[φ(t)]+lcos ϑsin[φ(t)]
(8)
(9)
式中:-4πR(t)/λ为t时刻Q点相位。将式(8)代入式(9)并对其求导,可以得到Q点回波多普勒频率为
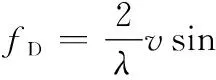
[cos ϑcosφ-cosαsin ϑsinφ]=fd+fmicro(t)
(10)
式中:第一项fd表示由平动引起的多普勒频率;第二项fmicro(t)表示由扑翼运动引起的微多普勒频率。若观测初始雷达径向对准该鸟类目标,即α=0,fmicro(t)可进一步化简为
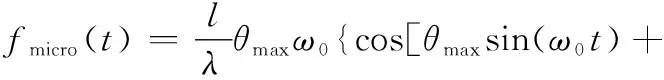
cos[θmaxsin(ω0t)+ϑ-ω0t]}
(11)
从式(11)可以看出,鸟类目标微多普勒频率至少以2π为周期进行周期性变化。
2 雷达回波信号时频分析
第1.2节给出了鸟类目标微多普勒模型,可基于此进行微多普勒效应仿真模拟。由式(11)可知,鸟类目标微多普勒频率是周期时变信号,若采用常规傅里叶变换对整个信号进行分析,只能得到信号在频域上的特性,不能获取信号在时域上的信息。因此,需要对鸟类目标微多普勒模型进行时频分析。本文采用物理意义明确的STFT时频分析方法,其原理是在时域内选取一个合适的窗函数,并对该窗函数进行采样。同时,对雷达回波信号y(t)进行采样,得到回波采样序列y。接着,利用窗函数对该采样序列进行截取,并假定截取序列是平稳的。通过不断移动窗函数得到不同时刻截取序列的傅里叶变换,这些傅里叶变换的集合就是对整段信号进行时频分析的结果[20]。本文选择高斯窗作为STFT窗函数。

xi=FHyi
(12)
式中:yi∈CL×1;H∈CL×L是由L个窗函数采样点构成的对角矩阵;F∈CN×L是傅里叶变换矩阵;xi∈CN×1是对应yi的待恢复微多普勒特征。进一步,可将上述公式改写为
(13)
式中:A′∈CL×N是STFT矩阵FH的伪逆。在实际探测鸟类目标时,由于周围环境存在大量噪声,雷达回波往往易受噪声及近场强杂波的影响。因此,将上式修正为
(14)
式中:ni∈CL×1表示噪声以及近场强杂波。由于观测噪声的影响,若直接求解,可能会出现频域分辨率下降等问题。由于微多普勒特征在时频二维平面具有稀疏特性,利用CS理论可知,可以把提取微多普勒特征转化为基于CS的特征增强问题[7-9]。
2017年,五建进行了区域化改革。区域化运行在促进“资源优化、责任落实”的同时,也尽可能地实现了“安居乐业、人文关怀”。“让员工可以在相对稳定的区域内工作是我们的一大初衷。这样可以对自己的职业进行有针对性地规划,比如在哪里工作,在哪里安家,孩子在哪里上学,如何照顾老人等等,解决了干事创业的后顾之忧。”蒋德军说。
为了方便解释后续参数更新过程,将全部M段截取信号排列成一个列向量,则有
Y=AX+N
(15)
式中:Y∈CLM×1;A∈CLM×NM是由A′构成的分块对角矩阵;X∈CNM×1;N∈CLM×1。
3 微多普勒特征贝叶斯学习
贝叶斯学习将关于未知参数的先验信息与样本数据相结合,基于贝叶斯原理得出未知参数的后验概率密度函数,并选择合适的贝叶斯推理方式求解,进而推断未知参数。
3.1 广义高斯先验概率模型
假设待恢复的微多普勒特征的每个元素均独立同分布。为了实现动态模拟散射场先验统计特性,自由选择先验模型,本文采用灵活自适应的GGD[21-22],其表示为
(16)

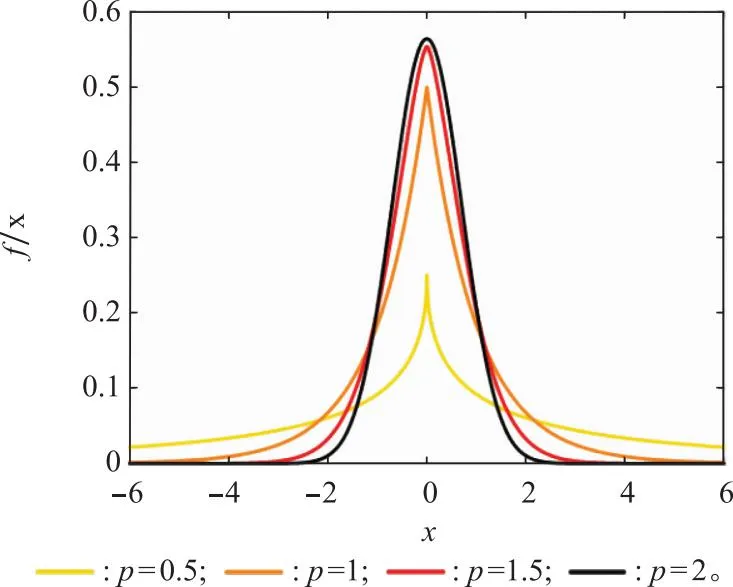
图3 一维GGD概率密度函数Fig.3 Probability density function of one-dimensional GGD
3.2 回波数据似然函数模型
通常,与模型相应的似然函数可写为
f(Y|X,β)=CN(Y|AX,βI0)
(17)
式中:CN(·)代表复高斯分布;β表示噪声方差;I0表示单位矩阵。
3.3 贝叶斯分层模型
由于鸟类目标微多普勒场景GGD先验与式(17)高斯似然函数不共轭,无法求得后验概率密度函数的闭合解析解[23]。针对此问题,采用贝叶斯分层模型对先验分布和似然函数分层以保证得到闭合解。由于GGD等价于p范数,为了能够更好地实现先验自适应,减少预固定先验影响,在贝叶斯分层模式下将形状参数p建模为均匀分布,即
(18)
式中:L[0,2]表示在区间[0,2]上的指示函数,当p在此区间时,L[0,2]=1,否则,L[0,2]=0。
为了减少系统误差,将尺度参数γ建模为无信息Jeffrey’s先验
(19)
式中:当γ>0时,LR+=1,否则为0。
通常,噪声服从加性高斯白噪声(additive white Gaussian noise, AWGN)。此时,可将噪声方差β建模为共轭逆Gamma分布
f(β|a,b)=TG(β|a,b)=
(20)
式中:TG(·)表示逆Gamma分布;a和b分别代表形状参数和比例参数,调整其数值可以改变Gamma分布的特性,通常令a=10-3,b=10-3,此时可以确保先验没有信息。
由此,通过对形状参数p和尺度参数γ以及噪声方差β进行层级建模,构建出了似然函数和先验分布之间的联系,为下节求解后验概率密度函数奠定了基础。根据式(16)~式(20),可得X,p,γ,β的联合后验分布为
f(X,p,γ,β|Y)∝
f(Y|X,β)f(X|p,γ)×
f(p)f(γ)f(β|a,b)∝
CN(Y|AX,βI0)GGD(X|p,γ)×
(21)
至此,鸟类目标微多普勒特征贝叶斯分层模型已构建完成。根据上述分层信息,可以使用有向无环图(directed acyclic graph, DAG)表示各个随机变量之间的关系,如图4所示。
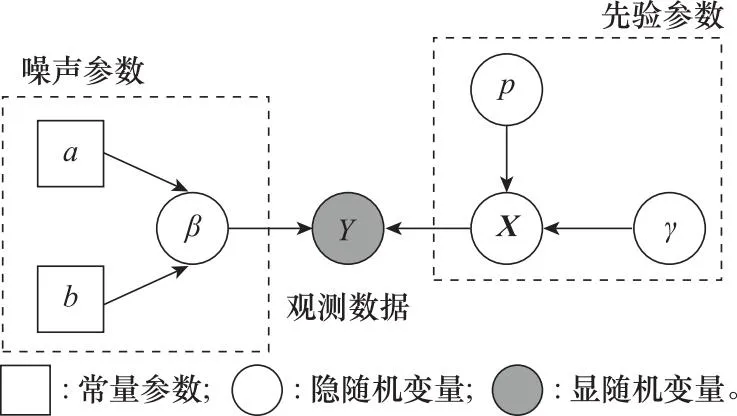
图4 概率图模型Fig.4 Probabilistic graphical model
图中,Y为显随机变量,表示雷达回波数据;X,p,γ,β为隐随机变量,X表示待恢复的微多普勒特征,p,γ,β为贝叶斯分层建模引入的3个超参数,分别为GGD先验的形状参数、尺度参数以及目标场景内加性噪声方差;a和b为固定常量参量。
3.4 后验概率密度函数求解
求解后验分布的方法可分为两类:近似确定性算法和统计采样算法[24-27]。其中,Gibbs采样作为一种典型的统计采样算法,基于马尔可夫链蒙特卡罗(Markov chain Monte Carlo,MCMC)[24]方法建立,能够在确定后验概率分布的条件下,通过循环采样获取参数估计值。变分贝叶斯期望最大化(variational Bayesian expectation maximization,VB-EM)是典型的近似确定性算法[25-27],可以实现隐随机变量推理,但其运算涉及矩阵求逆,求解复杂且效率低。为了降低运算复杂度,本文选择统计采样算法求解各个参数服从的条件后验分布。
根据式(17)和式(20),针对噪声方差进行边缘后验推导,结果如下:
f(β|Y,X,p,γ)∝
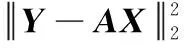
(22)
式(22)为常规逆Gamma分布,可直接根据该后验分布式进行Gibbs采样[15]。对于可变GGD先验形状参数p和尺度参数γ,由式(16)、式(18)和式(13)可得边缘后验分布为
f(p|Y,X,γ,β)∝
(23)
(24)
f(X|Y,p,γ,β)∝
(25)
ULA算法源自分子动力学,可用Langevin方程来表示随机粒子在流体中的布朗运动[28],其表达式为
(26)
式中:X代表粒子某一时刻的位置;m为粒子质量;-λ(dX/dt)表示流体分子粘滞力;η(X)表示分子热运动带来的热涨落力,通常表示为零均值高斯分布。求解式(26)即可得到粒子位置X分布。因此,模拟Langevin分子动力学,可以得到Langevin采样估计算法,该算法可以对以下形式对数凸分布进行采样
f(X)∝e-U(X)
(27)
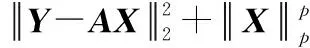
(28)
式中:ε表示更新步长;X(r-1)、X(r)分别为X第r-1次和第r次迭代后的采样值。考虑势能函数U(X)中含有p范数,此时势能函数U(X)很可能为非平滑函数,用ULA算法可能无法求解。因此,引入近端算子来解决非平滑势能函数不可微问题,其标准定义形式为
(29)
式中:U(X)为非平滑不可微势能函数;proxU(v)表示U(X)在v处的近端算子,近端算子可理解为某种求梯度的步骤,其中ε表示步长。由式(28)及近端算子与梯度之间的关系[29-30],近端ULA(proximal unadjusted langevin algorithm, P-ULA)中X的更新公式为
(30)
式中:proxU(X(r-1))为X在第r-1次更新时的近端算子,可用对偶前向后向(dual forward-backward, DFB)算法求解[29-31]。
4 贝叶斯增强算法流程
经过上述分析与讨论,所提雷达鸟类目标微多普勒贝叶斯增强算法流程如图5所示,主要包括初始化参数、超参数采样与微多普勒特征采样3个步骤。
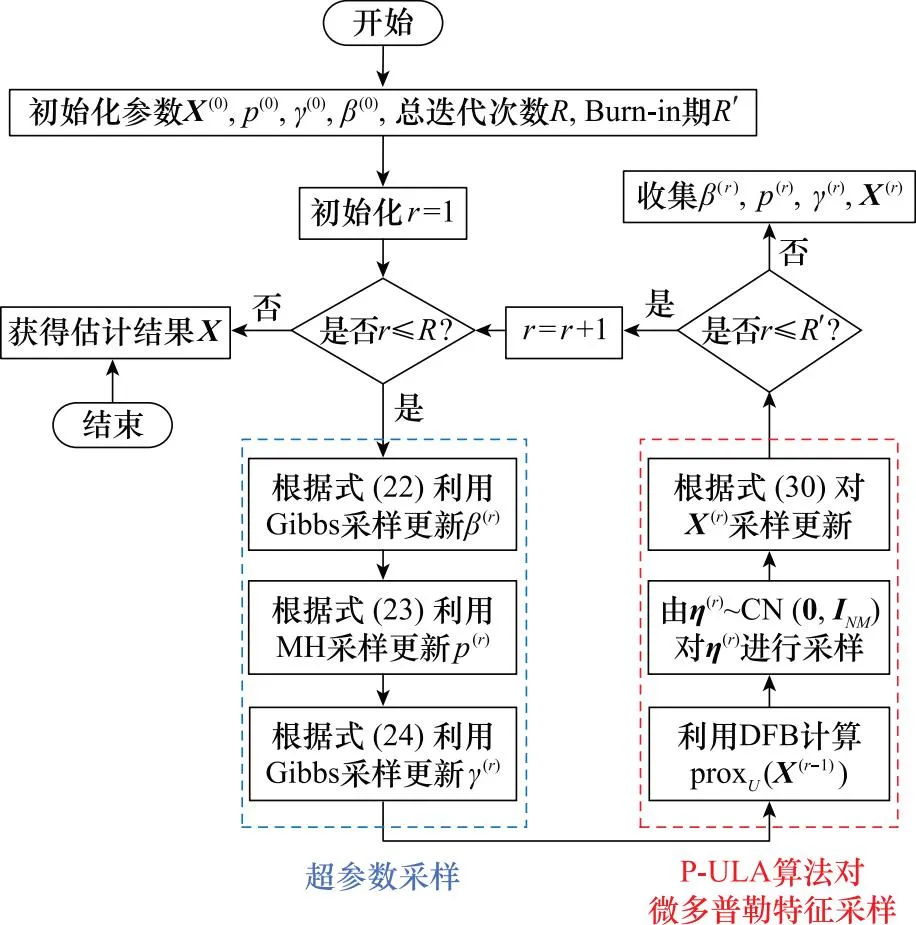
图5 雷达鸟类目标微多普勒特征贝叶斯增强算法流程图Fig.5 Flowchart of radar Bayesian enhanced algorithm of micro-Doppler feature of bird target
具体解释如下:首先,对待更新的参数集进行初始化,同时设置算法总迭代次数、Burn-in期。Burn-in期指在参数采样估计过程中,样本未收敛至目标分布前的阶段,所以在更新参数时应舍去该阶段样本数。
接着,进行超参数采样求解,如图5中左侧虚线方框所示。根据式(22),利用Gibbs采样器对噪声方差进行迭代采样更新。根据式(23)和式(24)分别利用MH和Gibbs采样算法迭代更新GGD先验形状参数p和尺度参数γ。
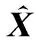
5 实验验证
根据上节所述概率模型,本文所提贝叶斯增强算法可以实现不同场景下鸟类目标微多普勒特征的增强。需要明确的是,本算法强调在时频域进行特征增强,不涉及时频分析前校正距离徙动等内容。换言之,本文所提算法仅仅考虑在进行时频分析时,在时频域上直接进行鸟类目标微多普勒特征增强。本章由仿真数据实验与实测数据实验组成。其中,仿真数据实验选择强杂波噪声、窄窗超分辨两种仿真场景;实测数据实验将以X波段雷达探测飞行鸽子数据为例,通过与STFT算法、凸优化算法[14]进行对比,验证了本文所提雷达鸟类目标微多普勒贝叶斯增强算法的有效性和优越性。
仿真数据实验中雷达工作在X波段,发射带宽为600 MHz,脉冲重复频率约为820 Hz,脉冲数为8 192,目标观测时间约为10 s。鸟类目标翅膀扑翼频率为1 Hz,正向平移速度为1 m/s,翅膀长度为1 m,上臂和前臂长度均为0.5 m,上臂扑打角度幅值为40°,上臂扑打角度滞后15°,前臂扑打角度幅值为30°,前臂扑打角度滞后40°,前臂扫角幅值为20°。在本文所提贝叶斯增强算法中,近端算子的步长为自适应调节,设置Gibbs采样老化期为40,设置总迭代次数为50。根据第1.1节给出的鸟类目标扑翼模型及以上参数,建立如图6所示的鸟类目标运动仿真简化模型[19]。其中,图6(a)为鸟类目标翅膀扑翼图,图6(b)为鸟类目标翼尖及肘关节飞行轨迹。图7为雷达追踪鸟类目标仿真及鸟类目标扑翼距离像。其中,图7(a)为雷达追踪鸟类目标仿真,雷达位置为(20,0,-10),图7(b)为鸟类目标扑翼距离像。
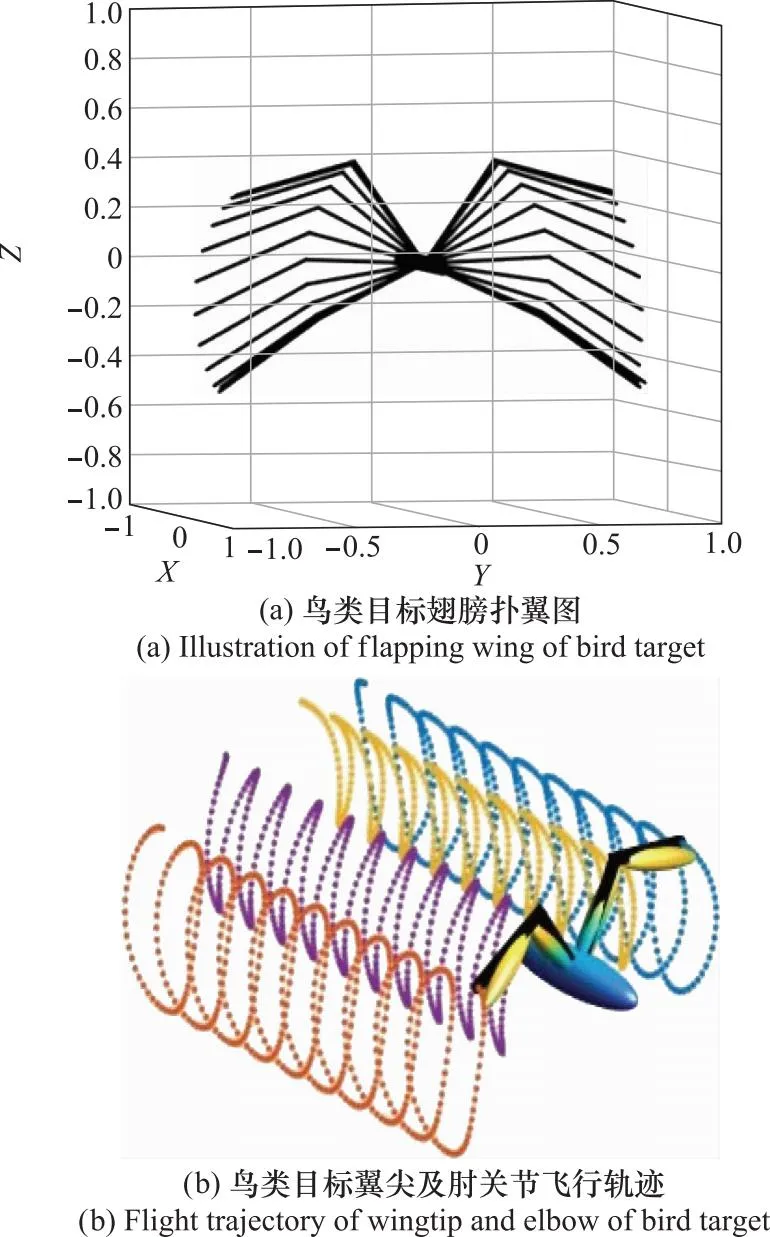
图6 鸟类目标运动仿真简化模型Fig.6 Simplified model of simulating motion of bird target
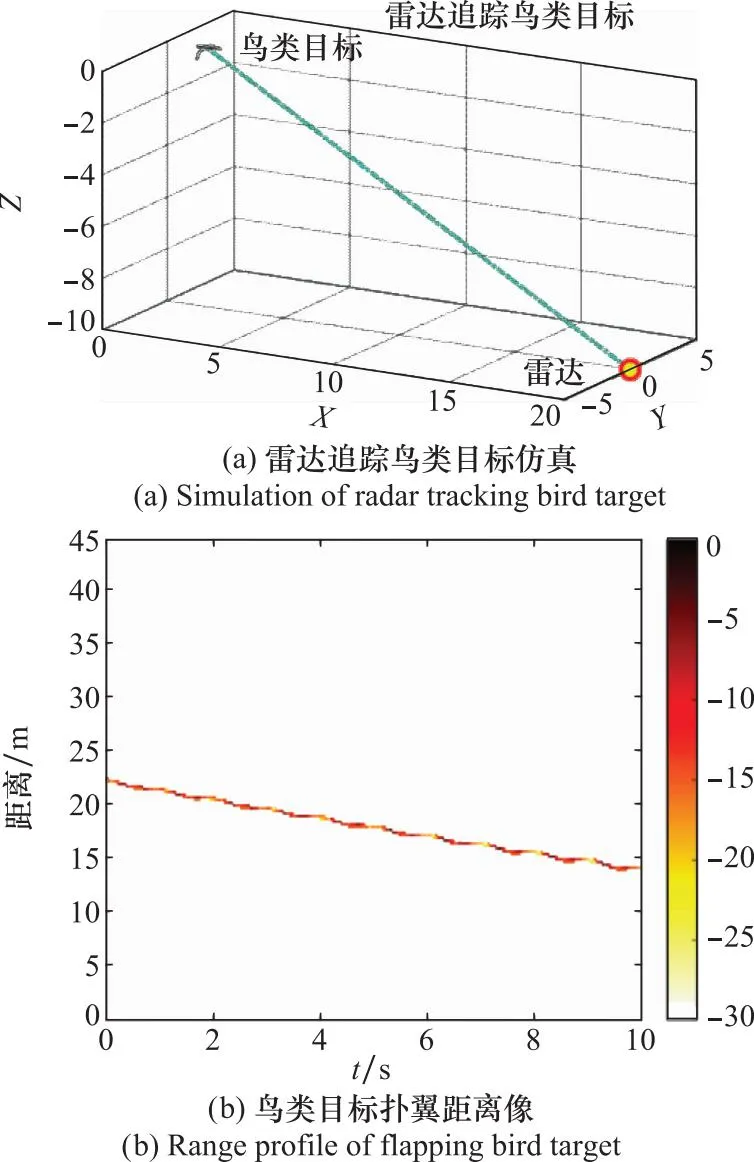
图7 雷达追踪鸟类目标仿真及鸟类目标扑翼距离像Fig.7 Simulation of radar tracking bird target and range profile of flapping bird target
5.1 仿真数据实验
本节由强杂波噪声与窄窗超分辨仿真实验组成,并定量、定性分析每组仿真实验的结果。
5.1.1 强杂波噪声仿真实验
为验证本文所提算法在抑制噪声的同时保留微多普勒特征完整性方面的有效性,本节以信噪比(signal-noise ratio, SNR)分别为0 dB、5 dB场景为例,将本文算法与STFT算法、凸优化算法作对比。图8和图9给出了SNR=0 dB、SNR=5 dB下运用STFT算法、凸优化算法以及本文所提算法得到的鸟类目标微多普勒特征结果。当SNR=0 dB时,图8(a)为采用STFT算法得到的结果,不难看出背景噪声斑点较多,鸟类目标微多普勒特征淹没在背景噪声中,难以有效识别鸟类目标。图8(b)为运用凸优化算法进行稀疏特征增强后的结果。从该鸟类目标微多普勒特征图中可以看出,尽管经过稀疏特征增强处理后,大量背景噪声被抑制,但鸟类目标微多普勒特征的连续性被破坏。图8(c)为运用本文所提算法提取鸟类目标微多普勒特征的结果,相较于图8(a)、图8(b),图8(c)不仅抑制背景噪声效果明显,而且保留了微多普勒特征更多的连续性,其连续性特征更加明显。
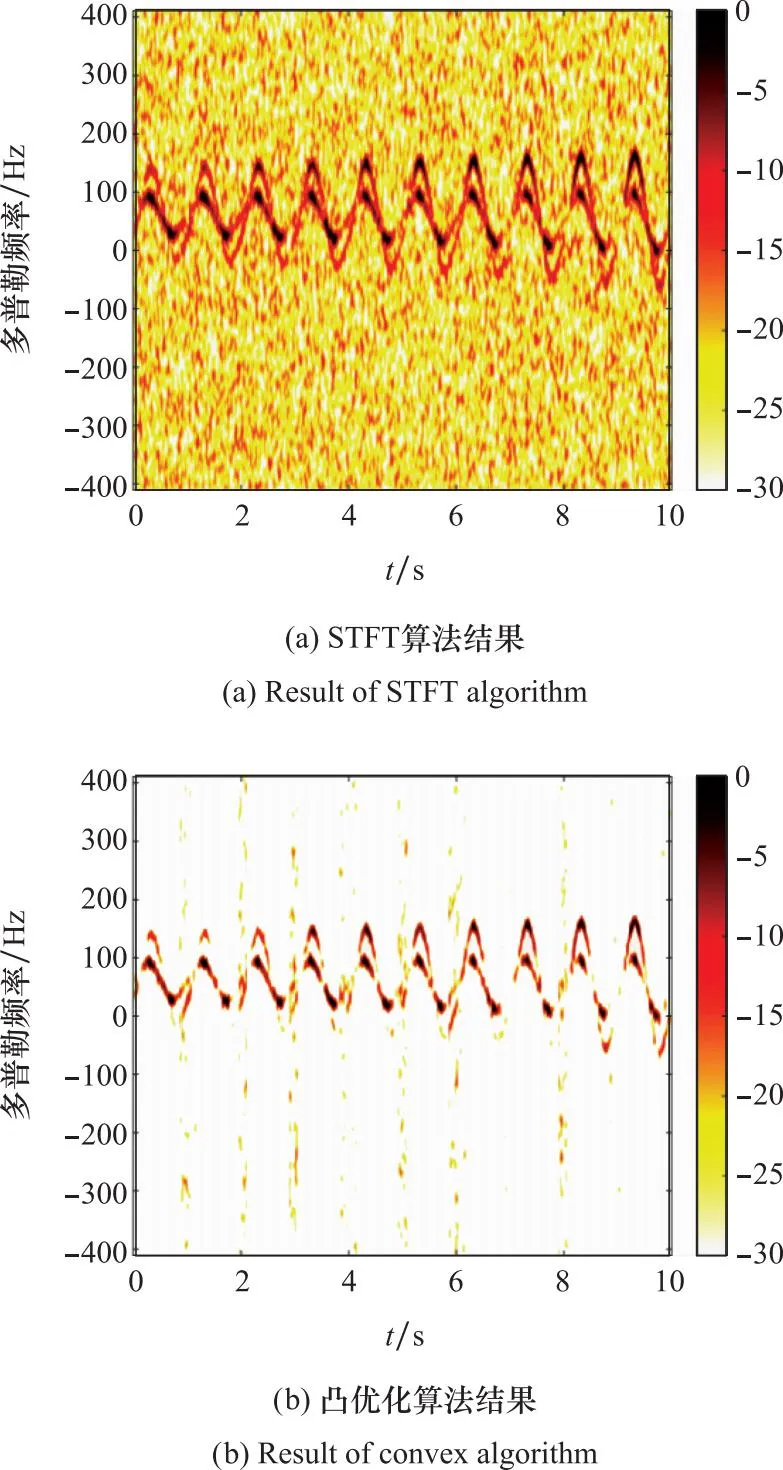
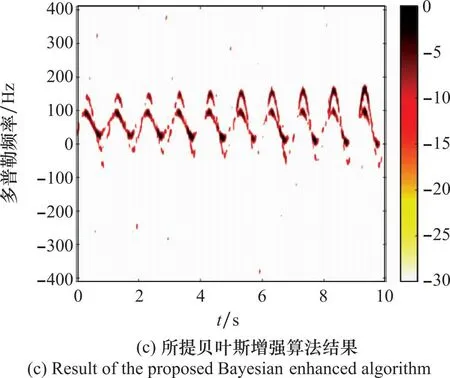
图8 SNR=0 dB时仿真数据实验结果对比Fig.8 Comparison of experimental results of simulation data with SNR=0 dB
为定量描述不同算法恢复微多普勒特征的性能,引入归一化均方误差(normalized mean square error, NMSE),其数学公式[15]为
(31)
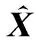
当SNR=5 dB时,不同算法提取的鸟类目标微多普勒特征结果如图9所示。从图9(a)、图9(b)、图9(c)可以看出,随着SNR的增大,所有算法恢复的鸟类目标微多普勒特征完整性均比图8有所提升。特别地,对于利用本文所提贝叶斯增强算法恢复的图9(c)结果,在有效抑制背景噪声的同时,保留了更多微多普勒特征的连续性。经过MCM仿真计算,图9(a)、图9(b)、图9(c)对应算法的NMSE分别为0.490 7、0.505 4、0.234 7,由此可见本文所提贝叶斯增强算法微多普勒特征恢复精度高。观察以上两组仿真实验结果,鸟类目标微多普勒特征由多组重叠类正弦波多普勒图形组成,每组多普勒图形中多普勒频偏最大的类正弦波图形为鸟类翅膀翅尖扑打所产生,由此可推算出该鸟类目标翅膀总长度为1 m,符合预设。而重叠在内部的类正弦波图形由鸟类翅膀前后臂间的节点扑打所产生,由此可推算出该鸟类目标翅膀前臂长度为0.5 m,符合预设。
图10给出了在一定SNR范围内,STFT算法、凸优化算法、贝叶斯增强算法恢复鸟类目标微多普勒特征性能曲线的对比示意图。继续沿用MCM仿真,采用NMSE评价不同算法在不同SNR条件下恢复鸟类目标微多普勒特征的性能。由图10可知,随着SNR不断增加,STFT算法的NMSE呈直线式下降,表明STFT算法易受SNR影响,对噪声敏感,算法恢复稳定性差。而凸优化算法虽然在低SNR条件下恢复性能优于STFT算法,对噪声不敏感且性能曲线平稳,但是在高SNR条件下,其仅能进行稀疏特征增强的凸优化算法,不能够满足恢复精度的要求。相比前两种算法,本文所提贝叶斯增强算法,不仅性能曲线相对平缓,不易受SNR影响,而且在NMSE数值上明显优于其他两种算法。综上所述,在不同SNR条件下,本文所提贝叶斯增强算法不仅能够以较高精度有效提取鸟类目标微多普勒特征,而且具有一定的性能稳定性。
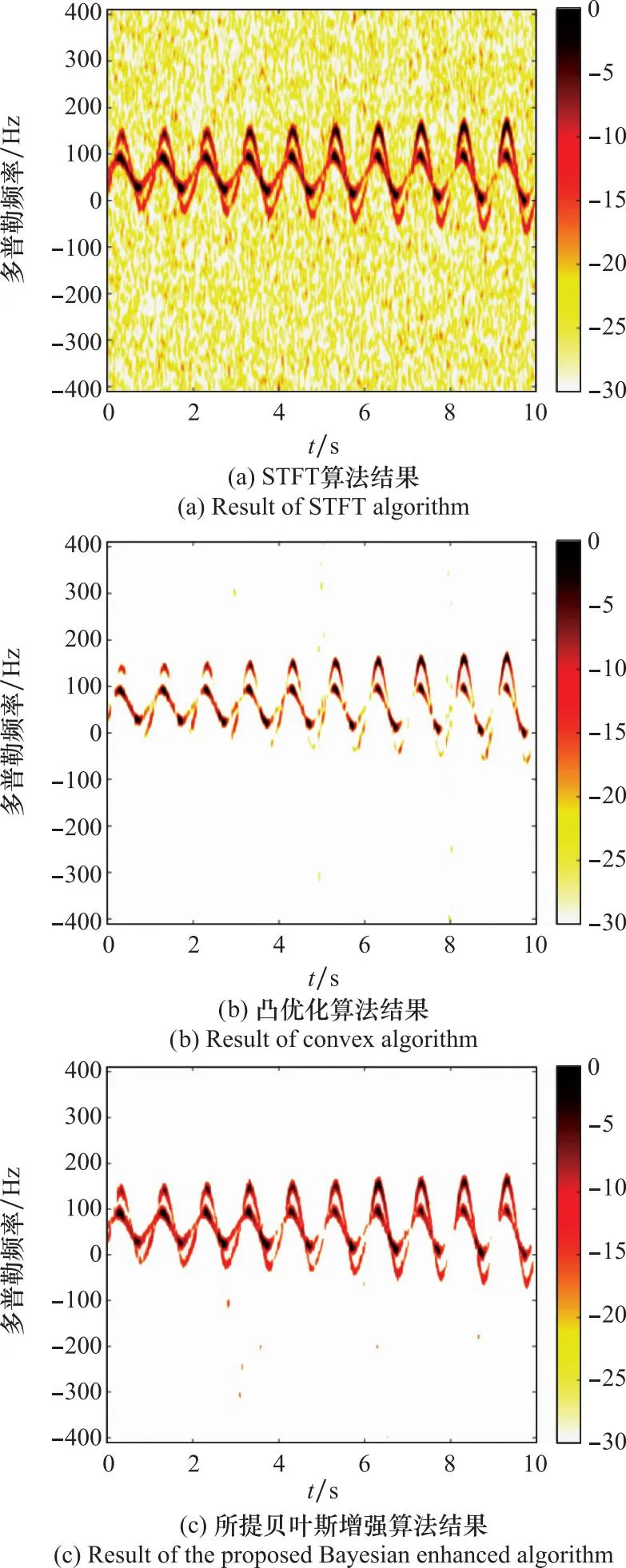
图9 SNR=5 dB时仿真数据实验结果对比Fig.9 Comparison of experimental results of simulation data with SNR=5 dB
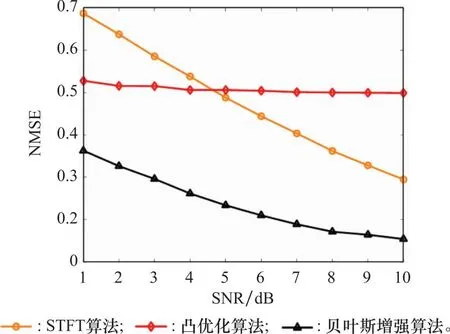
图10 不同SNR条件下不同算法的性能曲线对比Fig.10 Comparison of performance curves of different algorithms under different SNR conditions
5.1.2 窄窗超分辨仿真实验
为验证所提算法在超分辨方面的有效性,在SNR为5 dB前提下,将强杂波噪声仿真实验中采用的短时窗函数长度缩短至原来长度的50%,再将本文所提算法与STFT算法、凸优化算法作对比,考察各个算法恢复鸟类目标微多普勒特征的性能。图11(a)为运用STFT算法提取鸟类目标微多普勒特征的结果,由图11(a)可见,短时窗函数变窄使得微多普勒特征变得模糊,即频率分辨率降低,同时STFT算法无法抑制背景噪声,难以通过该微多普勒特征图准确获取与鸟类目标相关的特征信息。图11(b)为运用凸优化算法进行稀疏特征增强后的结果,此算法虽然能够有效抑制背景噪声,但同时也抑制了微多普勒特征的连续性,使得微多普勒特征不够连续,超分辨效果一般。图11(c)为运用本文所提贝叶斯增强算法进行特征增强后的结果。从图11中可以看出,该算法既能有效抑制背景噪声,同时又尽可能保留了微多普勒特征中更多的连续性,相较于图11(a)、图11(b),本文所提贝叶斯增强算法所恢复的微多普勒特征连续性更加明显,超分辨效果较好。经过MCM仿真计算,图11(a)、图11(b)、图11(c)对应算法的NMSE分别为0.674 1、0.553 3、0.510 8,验证了本文所提贝叶斯增强算法在超分辨方面的有效性。
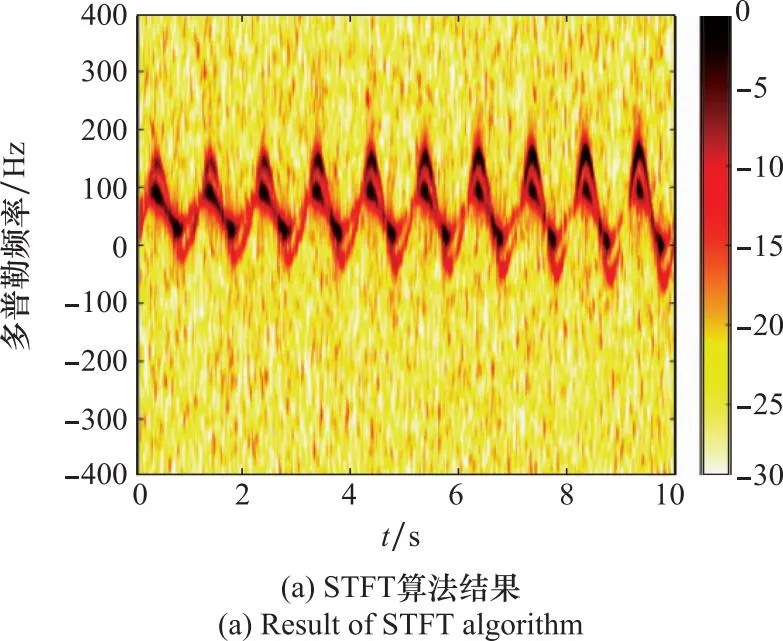
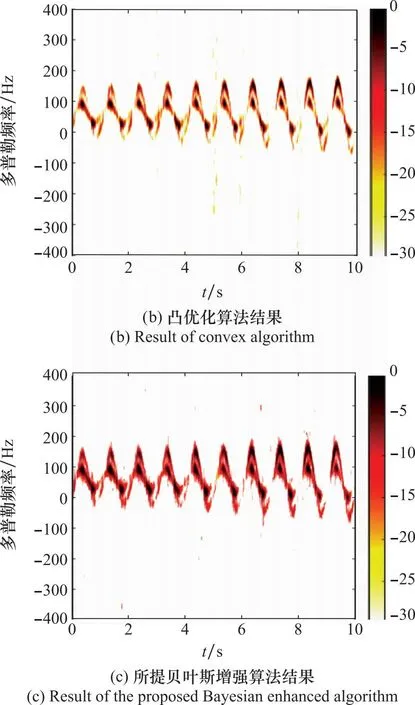
图11 SNR=5 dB时窄窗超分辨仿真数据实验结果对比Fig.11 Comparison of super-resolution experimental results of simulation data with SNR=5 dB and narrow window
5.2 实测数据实验
本节将雷达探测飞行鸽子实测数据用于验证鸟类目标微动信号模型的通用性与所提贝叶斯增强算法的有效性。该实测数据对应阵列雷达系统工作在X波段,发射信号瞬时带宽为16 MHz,阵列单元数目为16,工作模式为单发16。图12给出了该鸽子目标探测响应结果。其中,下面的线表示单天线目标探测响应结果,上面的线表示多天线目标探测响应结果。很明显,通过观察单天线目标探测响应结果,可疑距离单元445处的鸽子目标淹没在了近场强杂波中。在多天线目标探测响应结果中,虽然该鸽子目标探测响应强度得以提高,但近场强杂波的影响依然显著存在。因此,利用传统CFAR检测方法不易探测类似鸽子这种低慢小目标,而且容易导致虚警率高。接下来,考虑提取该鸽子目标微动特征来实现对其的探测。
图13给出了飞行鸽子的微多普勒特征图,其中图13(a)、图13(b)、图13(c)分别为由STFT算法、凸优化算法和本文所提贝叶斯增强算法提取的微多普勒特征结果。为了能够一致地评价各个算法的恢复效果,对每个算法恢复的微多普勒特征结果进行归一化处理。在图13(a)中,STFT算法作为线性运算,虽然运算效率快,可以实现多分量微多普勒特征提取,但是其恢复的微多普勒特征相对模糊,微多普勒特征周期性不明显,难以有效从图中获取该鸽子目标的特征信息。相比STFT算法,在图13(b)中,由凸优化算法恢复的微多普勒特征虽然在频率分辨率方面得到一定程度提升,但是造成了微多普勒连续性特征损失,同样不利于从其中准确提取该鸽子目标特征信息,甚至可能会遗漏重要的特征信息。相比前两种算法,由本文所提贝叶斯增强算法提取的微多普勒特征在有效改善频率分辨率的同时,保留了微多普勒特征更多的连续性,提高了获取该鸽子目标相关信息的准确性。由图13(c)所示,观测目标总时间约为3.3 s,由此可推算出鸽子扑翼的频率约为5 Hz,属于鸽子飞行时正常扑翼频率范围。因此,通过本文所提贝叶斯增强算法可以获得鸟类目标扑翼周期,以用于后续鸟类目标的检测与识别。综上所述,经过雷达探测飞行鸽子实测数据的验证,本文所提贝叶斯增强算法在处理实测数据时仍然具有一定的有效性。
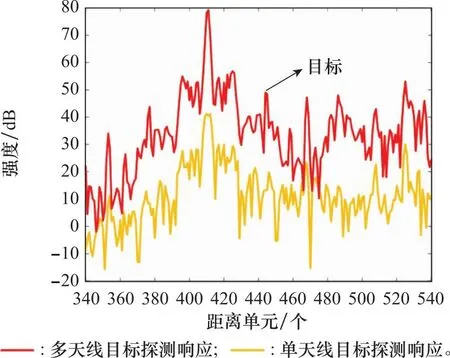
图12 鸟类目标探测响应图Fig.12 Figure of detection response of bird target
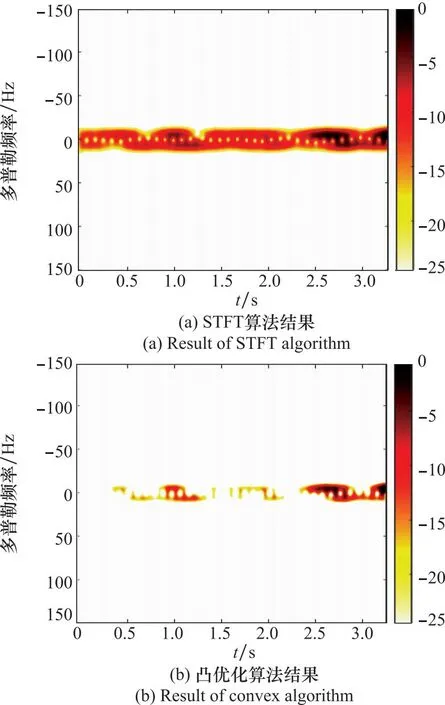
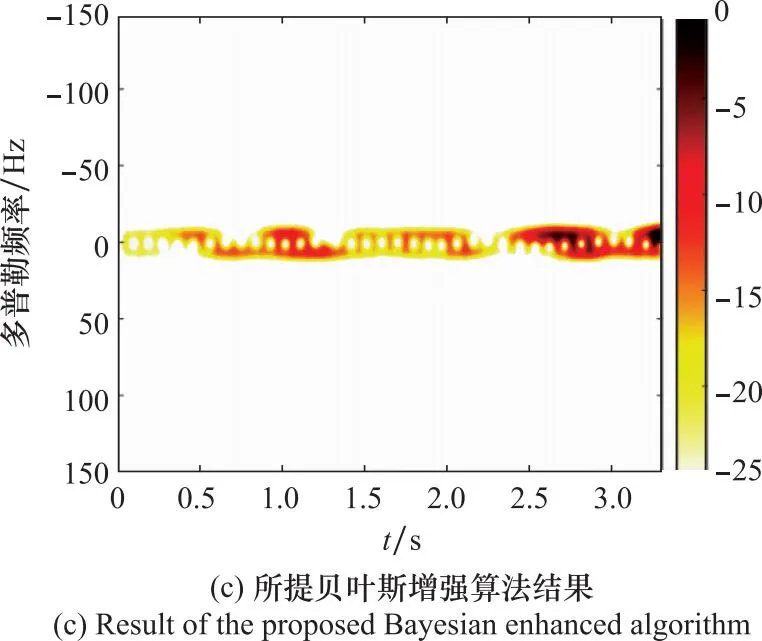
图13 实测数据实验结果对比Fig.13 Comparison of experimental results of measured data
6 结 论
针对鸟类目标RCS小、近场强杂波干扰等因素造成探测鸟类目标困难的问题,本文提出运用鸟类目标扑翼运动产生的微多普勒特征对鸟类进行探测与识别。首先建立鸟类目标扑翼模型,继而推导出鸟类目标雷达回波及微多普勒模型,最后针对STFT线性时频分析方法获取的微多普勒特征分辨率低、特征不明显以及场景复杂多变等问题,提出利用GGD对先验进行自适应建模,借助贝叶斯推理,采用P-ULA算法高效求解后验概率密度函数,在时频域实现鸟类目标微多普勒特征增强。经过仿真数据实验验证,在低分辨率、高噪声的情况下,本文所提算法可以得到特征明显的微多普勒特征。同时,本文所提算法在实测数据上依然可以有效提升微多普勒特征的分辨率,保留微多普勒特征更多的连续性。本文为雷达鸟类目标识别提供了新思路,在此基础上,可以研究更加复杂的鸟类模型以及提高时频分辨率的算法。同时,在利用本文所提贝叶斯增强算法进行特征增强时,虽然保留了连续性特征,但是损失了一部分结构性特征,有必要研究适用于更多特征的增强算法,这将是后续研究工作的重点。
