基于宽带极化纯度估计的极化测量定标修正
2024-01-30殷红成黄培康
白 杨, 殷红成, 黄培康, 刘 芳
(1. 中国传媒大学信息与通信工程学院, 北京 100024;2. 北京环境特性研究所电磁散射重点实验室, 北京 100854)
0 引 言
雷达目标极化散射特性通常用极化散射矩阵(polarization scattering matrix, PSM)表征,其随工作频率与目标姿态而变化,对于给定的频率和目标姿态特定取向,散射矩阵可表征目标散射特性的全部信息[1]。在实际工作中,由于极化散射特性及其产生机理的复杂性,通常需要通过实验测量来获取复杂目标的PSM。极化散射测量系统通常需要完成4种极化收发组合下对目标散射信号的获取,因此具备多通道能力是此类系统最显著的特征。极化散射测量及其系统使用的复杂性,造成了其测量误差模型相对于同极化测量更加复杂:由测量系统幅度与相位噪声引起的统计误差、系统线性误差,以及由有源器件引起的非线性误差等,都是影响极化散射测量不确定度的主要因素[2-3]。在诸多因素中,不同极化通道间的耦合与天线的极化纯度、收发隔离度等密切相关,构成了PSM测量中影响系统误差的主要因素[2]。开展测量时分别对环境、定标体和目标的各极化组合回波信号进行采集,通过定标体幅度-相位理论值求解复数形式的雷达极化系数矩阵(radar polarimetric coefficients matrix, RPCM),可以对目标的PSM求解,实现对测量系统的幅度-相位标定,通常可使目标测量结果不同极化分量间的能量隔离度达到40 dB以上[1,4-6]。
扩展目标是具备多个散射中心分布的复杂目标[1],其各个部位的散射中心随类型不同会产生不同的退极化现象[7-9]。根据Kennaugh[10]提出的最佳极化理论,以及Huynen[11]在此基础上提出的交叉极化概念,表明简单目标的交叉极化差别很大,复杂扩展目标的交叉极化也有明显差别,这就使得退极化效应成为可用于雷达目标识别的一种标志特征。在定标确定的极化隔离度下,各散射中心各极化分量间依然存在相互耦合的能量泄漏[12]。当弱散射中心退极化效应较为明显但强散射中心退极化效应不明显时,这种能量泄漏仍会使极化特性存在较大偏差,掩盖目标真实的极化散射现象,进一步影响基于极化特性的复杂目标的极化特征提取与识别的准确性。解决这一问题的思路,一方面是不断提高极化测量标定后的极化纯度,但是这种方法难度较大,且较难保证目标区域获得全面提升;另一方面是在一定的测量极化隔离度保障下,开展高分辨分析与修正[13],以进一步提升测量结果的准确性。
本文针对极化测量标定后PSM各分量间残余能量泄漏影响极化散射特性测量准确性的问题,提出了一种针对扩展目标极化散射测量误差的高分辨表征模型,进一步给出了面向独立散射中心的极化特性测量结果修正方法,并通过对典型目标实验数据处理前后的比对分析,验证了所提方法的有效性。
1 极化定标测量及误差
对复杂目标PSM的测量,需要利用具备多个极化通道的散射测量系统,完成信号极化调制、发射、散射信号接收和解调4个主要过程,测量过程原理如图1所示[8]。图1中,使用一组正交的线极化基表示电磁场的极化方式,其中水平极化用h(horizontal)表示,垂直极化用v(vertical)表示。当电磁信号在一个极化的发射通道和接收通道中传输时,可以用一个极化组合对其进行描述,如hv表示垂直极化发射、水平极化接收的信号。泄露现象的存在,会对另一个极化通道产生影响,形成影响极化测量精度的主要乘性误差。系统发射通道和接收通道存在电磁信号的泄露,加之目标区固有的背景散射,构成了重要的加性耦合误差[3,14]。为了准确获取复杂目标的极化散射特性数据,需要采用极化校准测量的方法开展实验,以修正上述误差。
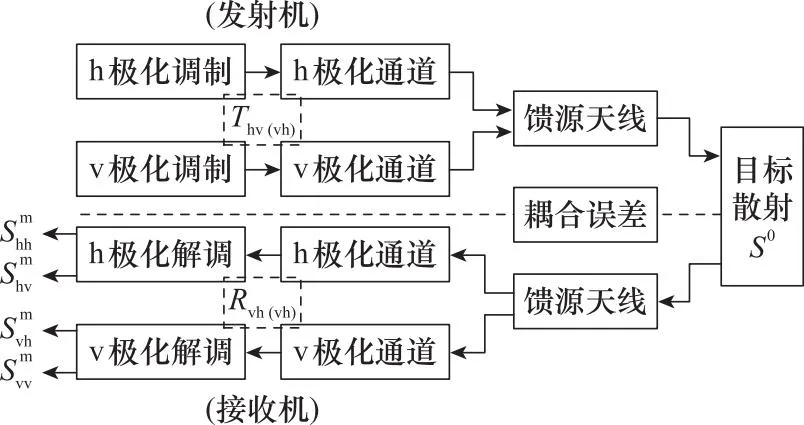
图1 PSM测量过程的原理Fig.1 Principle of PSM measurement process
极化校准测量运用最为广泛的误差模型描述为由系统接收极化误差矩阵R、目标极化散射矩阵S和系统发射极化误差矩阵T构成的RST模型。该模型由Sarabandi等[15]提出,能够描述被测目标PSM的测量至于理论值之间的量化关系,其表达形式如下:
Sm=I+RS0T
(1)
式中:Sm为目标测量的散射矩阵;I为加性误差矩阵,含馈源耦合、目标支架反射和微波暗室残余反射等;T为发射路径的乘性误差,含频响误差和交叉极化耦合误差;R为接收路径的乘性误差,含频响误差和交叉极化耦合误差;S0为目标真实的散射矩阵。
在进行目标散射矩阵测量时,会使用一个极化特性已知的目标来检验极化校准的效果,通常选择金属球或金属方板一类没有退极化效果的标准体[12]。由于测量系统是非理想的,以及测量结果存在误差,在实际情况下无法测得前述标准体的理论散射矩阵,会存在正交极化泄露。例如,直径300 mm金属定标球X波段的极化散射扫频雷达散射截面(radar corss section, RCS)的测试结果曲线如图2所示,由图2可知,在经过极化校准后,正交极化间的差异约为40 dB。这就意味着,当目标存在同极化分量较强的散射中心时,即使点目标测量达到了一定极化纯度,仍然会对相对较弱的正交极化散射中心产生比较明显的影响。因此,需要进行进一步修正,以提高对复杂目标全极化高分辨特征获取的准确度。
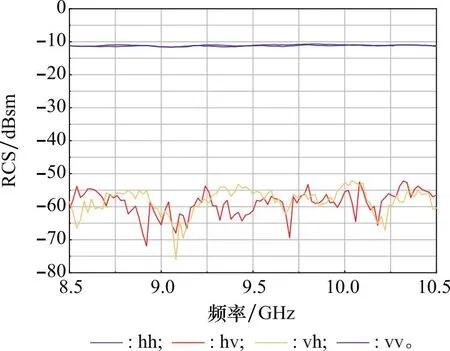
图2 直径为300 mm的金属定标球极化散射扫频测量结果Fig.2 Polarization scattering sweep frequency measurement result of a metal calibration ball with diameter of 300 mm
2 残余测量误差的表征与估计
2.1 残余测量误差的表征
理想的正交极化测量校准算法是不存在正交极化残余泄漏的,即对式(1)中T和R的求解是无偏的,但在实际测量中,这种假设是不可能达到的。为了在校准过程中显化残余误差的影响,假设T和R是可准确求解的,则校准后存在的正交极化残余误差可表征为叠加在目标散射矩阵上的一个误差矩阵,即
Sm=I+R(S0+S0_err)T
(2)
式(2)可进一步改写为
Sm-I=R(S0+S0_err)T
(3)
将式(3)展开为2×2阶矩阵表达,可得
(4)
由式(4)可知,为了求解目标真实的散射矩阵S0,需要求解组成I、R、T和S0_err的16个未知元素。考虑到加性误差可以通过环境重复测量后的矢量减法进行较好的消除,因此可以近似测得I中的4个元素,但仍需解决R、T和S0_err中12个误差参数的计算求解问题。S0_err中各元素的值与S0是相关的,每更换一个不同定标体,就会得到一组独立的S0_err,无法构成联立方程,进而无法求解。定义矩阵如下:
St=S0+S0_err
(5)
M=Sm-I
(6)
以及正交极化纯度
(7)
将式(7)代入式(5)并按照列向量整理,得
(8)
将式(6)和式(8)代入式(3),并按照列向量整理,得
(9)
其中,
(10)
2.2 正交极化纯度误差的估计
由于正交极化纯度的引入,式(9)相较于式(1)增加了4个未知量。理想状态下,在系统是收发互易性系统时,即T=RT时[2],式(1)的系数矩阵可通过测量一个非退极化校准体(如金属球、金属圆盘)和一个退极化校准体的不同旋转角度(如金属二面角),之后求解线性方程组获得[6,14,16-18],求解式(9)则需加测一个极化校准体。实际上,极化纯度与系数矩阵C的部分元素间为乘积运算,获得的是二阶多元方程组,求解较为困难。为了简化运算,可以先行求解系数矩阵C,再利用求解结果对不同的极化校准体进行测量,估计极化正交纯度误差。
针对系数矩阵C的测量校准方法可参见相关文献[3,6,17,19-21],此处讨论正交极化纯度的估计方法。根据式(8)可知,通过测量PSM已知的目标可以估计4个未知的正交极化纯度。观察等号右侧4×4矩阵的特点,可以使用完全退极化和完全不退极化的两种标体来直接估计4个正交极化纯度,如金属球、金属圆盘和滚转45°的金属二面角。金属球相较于其他同体积目标RCS较低,对其测量获得的残余正交极化散射分量较小,精度可能受到系统噪声、环境杂波等影响;金属圆盘RCS对姿态十分敏感,在测量中不易操作,因此宜选择金属二面角进行正交极化纯度估计。
金属二面角的姿态定义如图3所示,二面角每个平面的边长分别为a和b,将折边沿竖直z轴方向放置时定义为滚转角θ为0°。θ=0°时,电磁波沿二面角角分线-x方向入射时,二面角在光学区的PSM[5,17,20,22]为
(11)
式中:λ为测量的波长。当目标绕x轴旋转θ时,有:
(12)
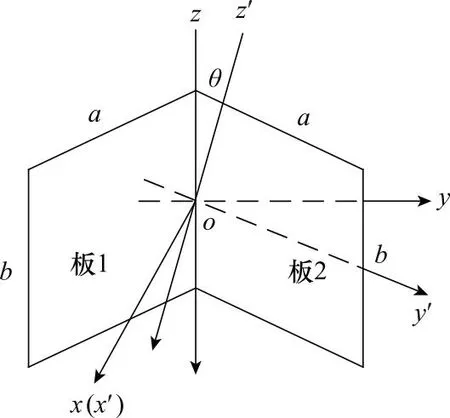
图3 金属二面角的姿态定义Fig.3 Attitude definition of metal dihedral
由式(11)和式(12)可得
(13)
将式(13)代入式(8)并整理,可得正交极化纯度的表达式为
(14)

根据式(14)中表达式的特点,θ可以选择0°、22.5°、30°、45°等特殊角度中的一个或多个求解正交极化纯度的值;也可以通过滚动二面角并进行连续均匀采样,之后求解其数学期望以减小估计误差,即
(15)

在获得正交极化隔离度后,即可通过式(8)对目标的极化校准测量结果进行修正。修正后的目标PSM各元素为
(16)
3 目标散射中心极化特性的修正
在高频区,目标总的电磁散射可以认为是某些局部位置电磁散射的合成,这些局部性的散射源通常被称为等效多散射中心,或简称多散射中心[5]。根据这一理论,可以认为复杂目标的散射矩阵是由多散射中心的复散射矩阵叠加而成的[16,23-26]。因此,可将RST模型改写为
(17)
式中:下标n代表第n个散射中心;RT0和RR0分别表示发射和接收天线到目标参考相位零点的距离;RTn和RRn分别表示目标的第n个散射中心到发射和接收天线中心的距离。可以看出,式(17)是对RST模型应用散射中心合成理论构造的测量模型,各变量定义相同。对于互易系统,背景环境散射和直漏路径能量可以合并到I中。
为了重点讨论散射中心极化泄漏的影响,首先假设天线形成的照射场极化性能是一致性分布的,即达到了理论远场条件,天线辐射场极化特性的空间分布可忽略,此时点目标不同极化的散射响应仅与入射波方向相关,与其空间位置无关。

(18)
其中,单个散射中心的各极化散射分量及正交极化纯度都包含了多个频率点的散射值,根据加法原理可知,式(16)对目标单个散射中心同样适用。对于目标总体PSMS0,以水平同极化hh分量快速傅里叶逆变换(inverse fast Fourier transform, IFFT)求一维距离像为例,有:
(19)
式中:*代表卷积运算。其他极化分量有类似结果。由式(19)可以看出,宽带条件下正交极化纯度积分变换形成的加权函数通过卷积运算对相应极化分量的每个分辨单元进行加权[27],之后合成对目标极化散射高分辨数据的测量修正结果。在此计算过程中,只有散射中心分布的分辨单元对式(19)的值有明显影响,其他分辨单元的计算结果都非常小。因此,对宽带高分辨测试结果的修正可以针对散射中心位置开展,对最终的结果精度影响不大,即
(20)
式中:N为修正目标散射中心的总数。
4 实验验证与结果分析
为了验证宽带极化测量误差修正方法的有效性,使用金属定标球、双金属二面角组合体和复杂金属类弹头目标模型进行了单站实测验证分析。实验在紧缩场微波暗室中进行,测试频率范围为8~12 GHz,频率点的采样间隔为1 MHz。测试系统采用ZVA40型一体化矢量网络分析仪构建,由微波功率放大器、极化控制器、距离门、目标支架转台和主控计算机等构成,具备极化单发双收和距离门选通测试能力,微波暗室的布置与测试系统的结构如图4所示[7]。测量时,被测目标放置在目标支架上,依次开展空暗室、定标校准体、修正校准体和目标的全极化测试,之后进行对目标和修正校准体的极化定标处理,最后进行宽带极化纯度估计和目标PSM的修正,获得实验结果,并分析修正效果。
4.1 正交极化纯度估计
实验中使用边长为200 mm的金属二面角进行正交极化纯度估计,在三定标体法[5-6,28-30]测量定标后,加测了连续滚动金属二面角的全极化响应。测量中使用的金属二面角如图5所示,为了方便和准确调整二面角的滚动角度,测试中的支撑采用带有精密角度刻度的可调节支座。通过式(15)可以求解本次测量正交极化纯度各量的估计,频域结果曲线如图6所示。

图5 金属二面角测试状态Fig.5 Metal dihedral angle testing status

图6 正交极化纯度估计结果(频域)Fig.6 Estimation result of orthogonal polarization purity(frequency domain)
4.2 金属球的修正结果
以直径为200 mm的金属定标球作为目标之一,验证方法的有效性。金属球类目标没有退极化效应,其PSM[1]形式为
(21)
式中:σ0为直径为200 mm的金属定标球在8~12 GHz频率范围内同极化RCS的理论值,约为-15.1 dBsm。
试验中,直接获得的金属定标球全极化RCS测试结果如图7所示。由图7可以看出,金属定标球的同极化RCS测试结果与理论值较为接近,频段内各点实测值的偶发误差在0.3 dB以内;正交极化RCS与同极化RCS的差值最小约为25 dB左右,这与图6中正交极化纯度各量的估计结果很接近,也说明本次测量的正交极化标定结果并不十分理想。通过式(6)对金属定标球测试结果的各极化散射分量进行修正,结果如图8所示。由图8可以看出,在修正后,正交极化RCS与同极化RCS的差值基本大于40 dB,同极化RCS的测试偶发误差在0.2 dB以内,验证了修正算法有较明显的效果。

图7 修正前的金属定标球测试结果Fig.7 Metal calibration ball test result before correction

图8 修正后的金属定标球测试结果Fig.8 Metal calibration ball test result after correction
4.3 双二面角组合的修正结果
为了验证修正方法对多散射中心分别修正的有效性,设计了带有一定滚转角的金属二面角组合体目标试验,其结构示意图如图9所示。测试时,电磁波沿-x轴方向入射,z轴方向为垂直极化v方向,两个金属二面角的角分线沿x轴方向放置,二面角A由边长为120 mm的正方板组成,折线沿z轴方向竖直,二面角B由边长为80 mm的正方板组成,折线绕x轴旋转与z轴形成2.5°夹角。两个金属二面角中心在xoy平面内,二面角A中心坐标(xA,yA)为(300 mm,200 mm),二面角B中心坐标(xB,yB)为(-450 mm,-300 mm)。

图9 金属二面角组合体结构示意图Fig.9 Schematic diagram of metal dihedrals angle combination structure
金属二面角组合体理论上可以形成两个较强的散射中心,由式(13)可得其各自散射矩阵的模矩阵近似为
(22)
实际测得的一维距离像曲线如图10所示,从图10中可以清楚地看到两个散射中心的相对位置和各极化组合的散射强度。受到图形显示空间的限制,图10仅标记出了部分极化的散射中心幅度值,全部的散射中心峰值结果如表1所示。

图10 金属二面角组合体全极化一维距离像(修正前)Fig.10 Fully polarized one-dimensional range profile of metal dihedral angle combination (before correction)

表1 金属二面角组合体一维距离像各散射中心峰值(修正前)
根据表1数据可以求得各散射中心实测散射矩阵的模矩阵为
(23)
对比式(22)和式(23)可以看出对两个散射中心的测试结果存在一定误差,利用第4.2节所述方法,根据式(20)对测试结果进行修正,散射中心峰值结果如表2所示,获得的一维距离像曲线如图11所示。

表2 金属二面角组合体一维距离像各散射中心峰值(修正后)

图11 金属二面角组合体全极化一维距离像(修正后)Fig.11 Fully polarized one-dimensional range profile of metal dihedral angle combination (after correction)
根据表2数据可以求得各散射中心修正后散射矩阵的模矩阵为
(24)
对比式(22)和式(24),可以看到两个散射中心的各极化分量经过修正后更接近于理论值,数据的正交极化纯度相应提高,强极化散射分量对弱极化散射分量的影响减小。
4.4 对复杂目标的实测验证
实验中采用的验证目标是全金属的类弹头模型,长度约4 500 mm,筒体直径约为800 mm,带有4个模拟方向舵结构,其外形尺寸如图12所示。
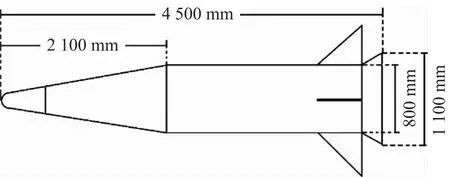
图12 全金属类弹头模型外形示意图Fig.12 Outline diagram of all metal warhead-like model
对实测结果直接进行二维逆合成孔径雷达(inverse synthetic aperture radar, ISAR)成像处理,成像中心视角沿模型头部0°方向,成像带宽4 GHz,成像孔径角30°。以hh极化二维像的最强散射中心为参考,对全部极化分量的像进行归一化处理,结果如图13所示。图13中,红色框线标记的散射中心是目标头部球头锥及其后边缘产生的,按照式(18)的描述,可求得这个局部的合成散射矩阵的模矩阵为
(25)
根据球头锥头部的散射机理,不应存在较强的退极化效应,但此时结果的正交极化差异仅为约27 dB,因此需要进行修正。
修正后的目标二维IASR成像结果如图14所示。由图14可以看到,两个交叉极化分量红色框线部分的散射中心强度明显减弱,同极化分量基本没有影响。再次求得这个局部的合成散射矩阵的模矩阵为
(26)
此时的正交极化差异为48 dB,验证了修正方法的有效性。
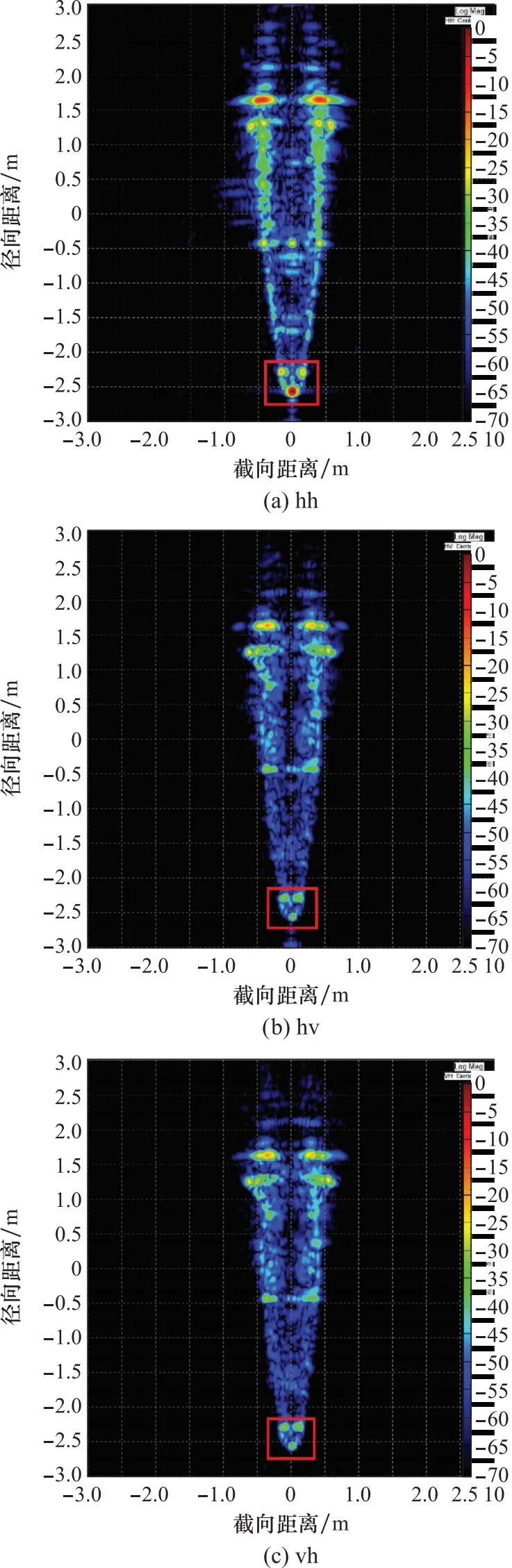

图13 金属类弹头模型的二维ISAR成像(修正前)Fig.13 Two-dimensional ISAR image of metal warhead-like model(before correction)


图14 金属类弹头模型的二维ISAR成像(修正后)Fig.14 Two-dimensional ISAR image of metal warhead-like model (after correction)
5 结 论
本文针对扩展目标宽带极化散射特性测量中,极化测量定标后仍存在正交极化分量互扰进而影响目标极化特性精度与特征判别的问题,由极化测量定标原理与宽带高分辨测量模型表征入手,阐述了干扰量的产生原因以及对测试结果的影响机理,提出了通过增测标准目标进行正交极化纯度估计进而修正复杂目标极化测量结果的方法,并通过对标准球体、二面角组合体和类弹头模型3类目标的实测,完成了对方法有效性的验证分析。与既有目标极化散射测量定标方法相比,本文所提方法丰富了复杂目标宽带极化测量误差的表征描述,在具体目标的既有定标精度限制下,利用极化纯度开展面向宽带测试结果的误差估计和修正,进一步减小了系统非理想因素对测试的影响,并可针对目标散射中心开展局部修正,特别适合于在扩展目标各部分结构散射测试结果极化分量差异与测量极化纯度可比拟时,提高PSM测量定标精度,本文所提方法对提高扩展目标极化散射特性静态测量获取精度、提升目标宽带极化特征精细化研究而言,具有一定的实用价值。
