不同GNSS在高纬度地区时间传递性能分析

陶琳琳,涂 锐,张鹏飞,左 航,王培源,方 婧

(1.中国科学院国家授时中心,西安 710600;2.中国科学院大学集成电路学院,北京 100049;3.中国科学院精密导航定位与定时技术重点研究室,西安 710600)

0 引言

基于全球卫星导航系统(global navigation satellite system,GNSS)的高精度时间传递是全球各守时实验室参与国际标准时间(coordinated universal time,UTC)计算和保持时间同步的关键技术之一,对推进国家军事战略水平、科技快速发展具有重要意义[1]。该技术主要包括共视[2]、全视[3-4]、载波相位时间传递技术[5-6]。共视是指两台GNSS接收机在同一时刻观测到一颗或多颗相同卫星,通过卫星钟这一公共参考源交换两地原子钟的时间偏差。但因该方法受作用范围限制,众多学者采用全视法,即直接观测所有卫星后求解该地时间与卫星星历参考时间的差值。在传统全视方法的基础上增加载波相位观测量的时间传递方法,称为载波相位时间传递方法,该方法与导航定位中的精密单点定位(precise point positioning,PPP)技术原理一致,因此又将载波相位时间传递称为GNSS PPP 时间传递。目前,GNSS PPP时间传递技术是全球卫星导航定位技术在高精度时间传递领域的主要研究方法之一,基于该方法可实现亚纳秒级精度的时间传递,同时具有短期稳定性高、数据处理较简单、连续性好、成本较低等特点。

随着美国全球定位系统(global positioning system,GPS)的现代化发展,俄罗斯卫星导航系统(GLONASS)的逐步完善,欧盟伽利略卫星导航系统(Galileo)的稳步推进以及我国北斗三号的建成,诸多学者在不同系统GNSS PPP载波相位时间传递领域开展了一系列研究工作。Ge等[7]选用CEBR,AGGO,BRUX,KIKU等多个中低纬度测站进行GLONASS的PPP时间链路传递,表明GLONASS的PPP时间传递与GPS/GLONASS PPP时间传递的标准差差值大约为0.4 ns;Zhang等[8]研究了附加先验信息约束的Galileo载波相位时间传递,研究表明长基线USN8-NTS1链路附加先验信息约束结果的频率稳定度明显优于未加约束的结果;Qin等[9]在BDS-2,BDS-2+BDS-3,BDS-3 和GPS 系统时间传递频率稳定性上展开分析,表明BDS-3在时间间隔分别为1 000 s,10 000 s和86 400 s时与GPS系统相比,链路稳定性的改善幅度分别为22.91%,38.40%和19.03%,与BDS-2 相比改善幅度分别为40.08%,34.06%和10.90%。

但是以上当前关于高精度时间传递性能的研究主要是对中低纬度地区的测站,在高纬度地区测站开展的研究较少。由于GNSS星座构型不同,高纬度地区可视卫星结构也存在较大差异。众多学者研究了高纬度地区不同GNSS精密定位的差异,首先在高纬度地区卫星观测数据方面,左宗等[10]对极区北斗卫星数据质量进行了分析,并与中低纬度地区载波相位观测量残差值对比,认为极地地区的BDS载波相位观测量残差整体比中低纬度小。除此之外,杨元喜等[11]指出高纬度地区与中低纬度地区相比的主要问题,虽然具有更多的可视卫星,但多数卫星高度角较低,在北纬75°时卫星的最大高度角低于70°,在北纬85°时,卫星的最大高度角仅为50°。高纬度地区在时间传递方面的研究并不多见,不同系统之间时间传递性能的差异也尚不清楚,需要进行深入研究。

同时,在高纬度地区卫星高度角较低,高度角的合理选择会涉及误差的放大和可视卫星增多之间的权衡问题。佘娣等[12]研究表明,对流层折射误差随卫星高度角的减小而增加,且当卫星高度角较小时误差急剧增大;丁朋辉等[13]和Beutler等[14]研究了低高度角信号的截止角选择对于可见卫星数、精度衰减因子等的影响。在高纬度地区合适的截止高度角设置方面,周润扬等[15]研究表明5°是最适合高纬度地区BDS/GPS定位的截止高度角;任超等[16]分析了低高度角对提高对流层估计精度的影响,并指出当截止卫星高度角为5°时对流层估算精度和高程定位精度更高。因此,有必要分析不同截止高度角对高纬度地区GNSS PPP 时间传递性能的影响。

本文主要分析了不同GNSS系统在高纬度地区的时间传递性能,并根据高纬度地区可视卫星高度角低的特点,对比分析了5°,10°,15°和20°不同截止高度角条件下不同GNSS系统时间传递链路稳定性。

1 PPP时间传递原理

GNSS载波相位时间传递方法与卫星导航定位中的PPP原理基本相似,但一般会有外接时间和频率的接入,用户可获得基于本地时频系统提供的高精度时间标准和频率标准的伪距和载波相位观测值,再结合国际GNSS 服务中心(international GNSS Service,IGS)提供的精密卫星轨道和钟差产品进行PPP解算,分别获得两地本地参考时间尺度与IGS参考时间尺度的差值。

PPP载波相位时间传递采用双频无电离层组合消除电离层一阶影响后,其观测方程可表示为

式中:s,r,j分别表示卫星、接收机、所采用的频率;表示无电离层组合伪距观测量、无电离层组合相位观测量;ρ表示卫星和测站之间的几何距离;δts,δtr表示卫星端钟差和本地接收机钟差;Tsr为对流层延迟误差;λ为载波相位波长;Nsj表示相位模糊度参数;εP,j,εL,j分别表示伪距和载波观测值噪声。

将观测方程(1)线性化,可将未知参数表示为

式中:X是待估计参数矢量,x,y,z为待估计测站坐标。在参数求解中,地球潮汐、相对论效应等误差均使用模型加以改正[17]。

PPP解算出的测站接收机钟差即为本地接收机时钟与参考时间基准的偏移量,两地接收机钟差分别为

式中:δtr1,δtr2分别为两地接收机钟差,Tref为参考时间基准,T1,T2分别为两地原子钟的时间偏移量。

再将得到的接收机钟差进行差分,得到的两地时间传递量为

式中:δt1,2为两地时间传递量,TDelay为两地接收机系统的相对硬件时延。

高精度时间传递延迟的测量目前主要有两种方法:一种是利用参考时频传递设备与待校准时频传递设备进行共钟差实验,另一种方法是利用GNSS 信号模拟器对时频传递设备进行绝对校准。相关研究表明,延迟量通过校准后相对稳定,因此本文中暂不考虑这部分因素对时间传递的影响。

2 高纬度地区时间传递实验

为对比分析不同系统(GPS,GLONASS,Galileo,BDS)载波相位时间传递性能,分别选取南纬地区高纬度测站OHI3、北纬地区高纬度测站YEL2、中心节点测站KOUR 三个测站,所选测站均外接氢原子钟,接收机初始截止高度角设置均为零,实验采用的时间段为GPS,Galileo,BDS 三个系统2022年12月9日—2022年12月29日21天数据,考虑到GLONASS系统在部分时间段内可用卫星数目不足4颗,采用了2022年12月15日—2022年12月20日6天数据,测站位置分布如图1所示,测试站点配置信息和数据处理策略分别见表1和表2。

表1 测站信息表Tab.1 Station information table

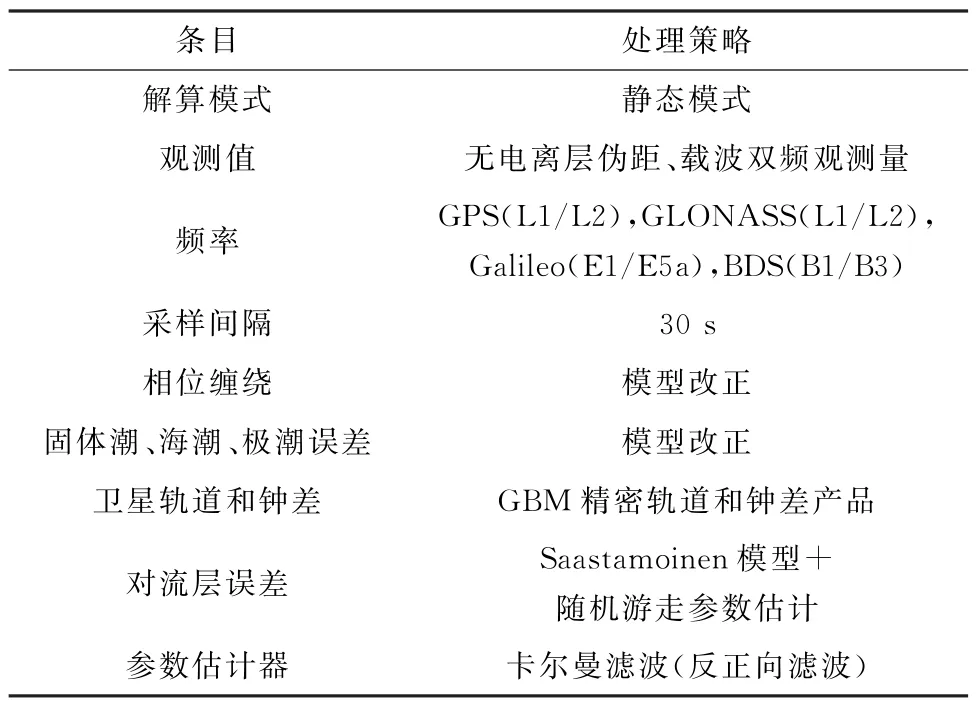
表2 数据处理策略Tab.2 Data processing strategy

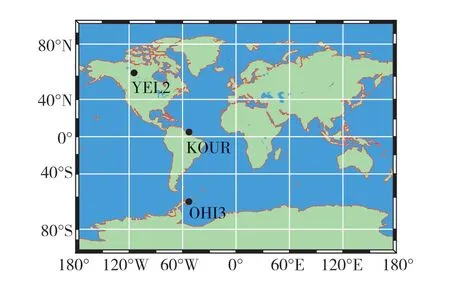
图1 实验所选测站站点分布图Fig.1 Distribution map of selected test stations in the experiment

3 卫星观测数据分析

在进行PPP时间传递性能评估之前,先从测站的卫星天空视图、卫星数、时间精度因子(time dilution of precision,TDOP)值三个方面对观测数据展开分析。

3.1 卫星天空图

天空视图展示的是测站上观测到的所有卫星一天的运动轨迹,实验中选取的三个测站2022 年12月15日的天空视图如图2所示。

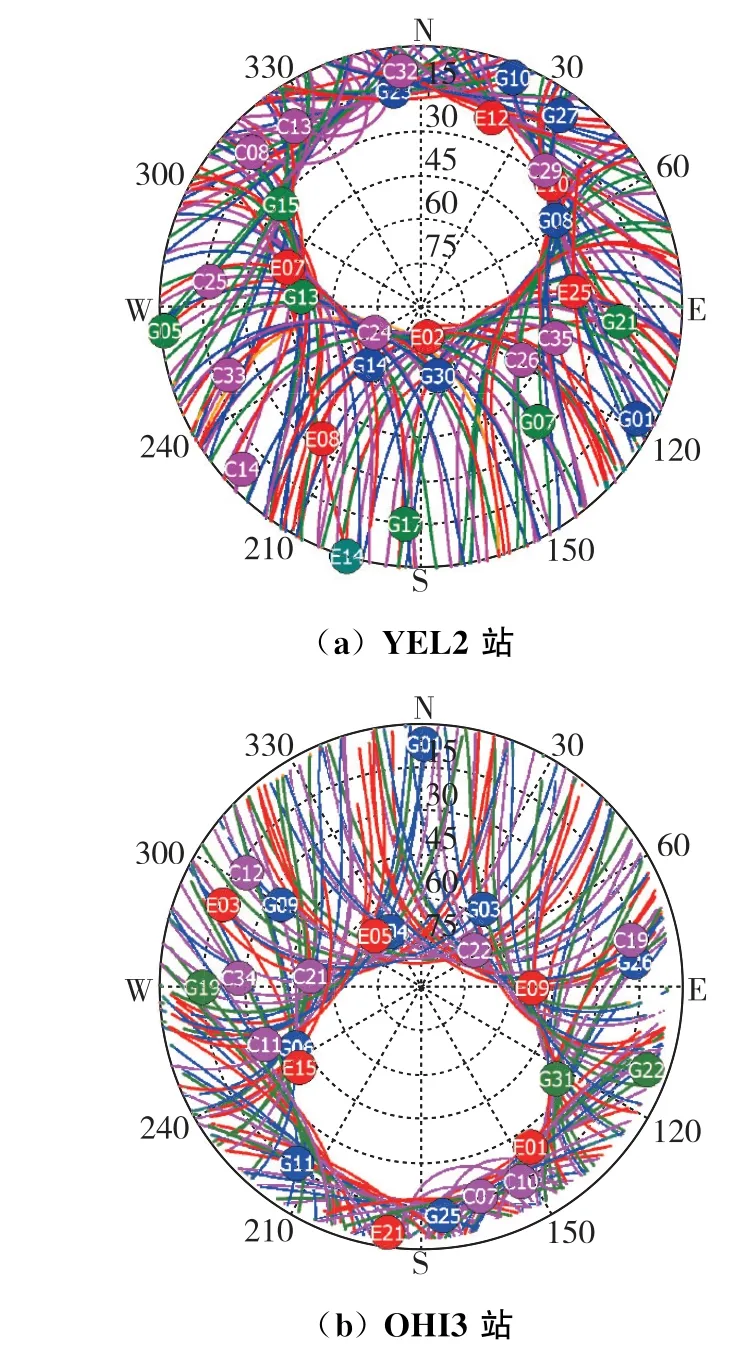
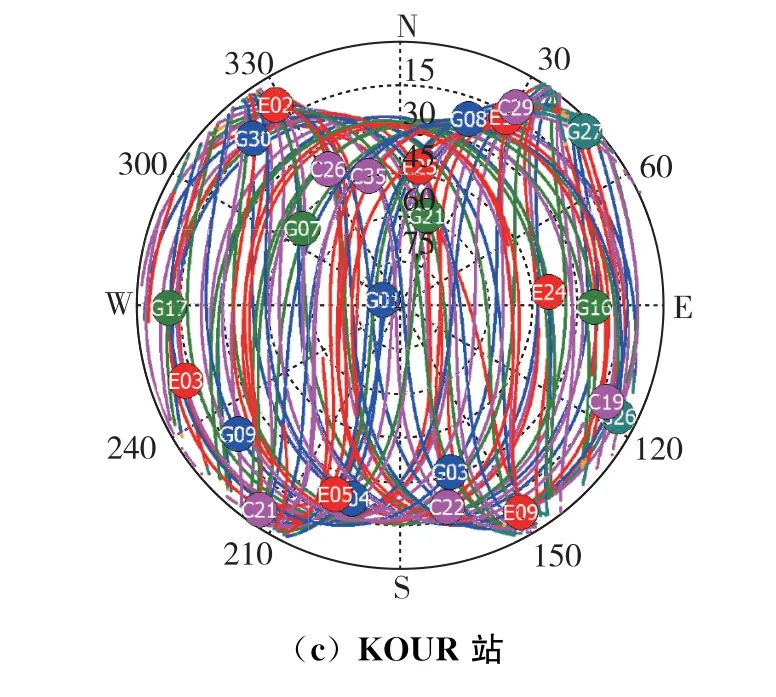
图2 实验中选定三个测站的卫星天空视图Fig.2 Satellite sky view of three selected stations in the experiment

由图2可知,从总体上看,三个测站观测的卫星数目均较多,且当高度角较低时,仍有较好的卫星可见性。

从具体上看,中低纬度地区KOUR 测站除了观测不到南北两极的卫星外,在其余方位都能收到较多的卫星,且卫星高度角都较高,没有低于30°高度角的卫星。相比之下,南半球高纬度地区OHI3测站在南部大高度角可视卫星较少,多数卫星高度角在30°以内,各个系统可视卫星数均较多,且在不同方位区域卫星分布均匀;北半球高纬度地区YEL2站在北部的可见卫星数较少,且卫星高度角较低,但整体不同方位区域卫星分布仍较为均匀。

由以上天空视图可看出,高纬度地区和中低纬度地区测站的可视卫星分布有很大差异,为进一步分析差异,3.2节对高纬度地区的卫星数及TDOP值展开研究。

3.2 可用卫星数与TDOP值

在GNSS中常用精度衰减因子(dilution of precision,DOP)值描述卫星的空间几何构型。根据所表征特性不同,DOP值又分为定位精度因子(position dilution of precision,PDOP)、垂直精度因子(vertical dilution of precision,VDOP)、水平精度因子(horizontal dilution of precision,HDOP)、时间精度因子(TDOP)等。PPP精密时间传递中卫星的数目和空间分布对于接收机钟差的影响常用TDOP衡量,因此重点对影响其时间传递精度的TDOP进行分析。

因每天观测得出的卫星数、TDOP 值变化相差不大,为了便于展示卫星数在不同历元的变化情况,图3和图4 给出了截止高度角为10°时,OHI3和YEL2测站在2022年12月15日一天内各系统观测的卫星数量、TDOP值变化情况,表3和4统计了OHI3,YEL2测站GPS,Galileo,BDS系统2022年12月9日—2022年12月29日21天的不同截止高度角下的卫星数、TDOP 的平均值,GLONASS系统2022年12月15日—2022年12月20日6天的不同截止高度角下的卫星数、TDOP 的平均值。由图3可以看出,当截止高度角为10°时,各系统观测的卫星数均大于4 颗,可进行PPP 解算。其中GPS的卫星数目较多,可用卫星数大约为7～12颗,Galileo系统的卫星数略低于GPS,在6～9颗左右。同时可以看出OHI3站北斗的卫星数历元间变化较大,在一天内最少为6颗,最多为14颗。YEL2站北斗的观测数目大约在5～13颗,历元间的卫星数目仍变化较大。各个测站的GLONASS 系统卫星数大多在4～8颗,均低于其他系统。且由图3和图4可以看出,高纬度测站的TDOP值在部分历元明显高于其他历元,因为在该历元参与解算的卫星数较少,部分历元卫星数仅有4颗,此时卫星几何构型较差,TDOP值出现大幅度抖动。

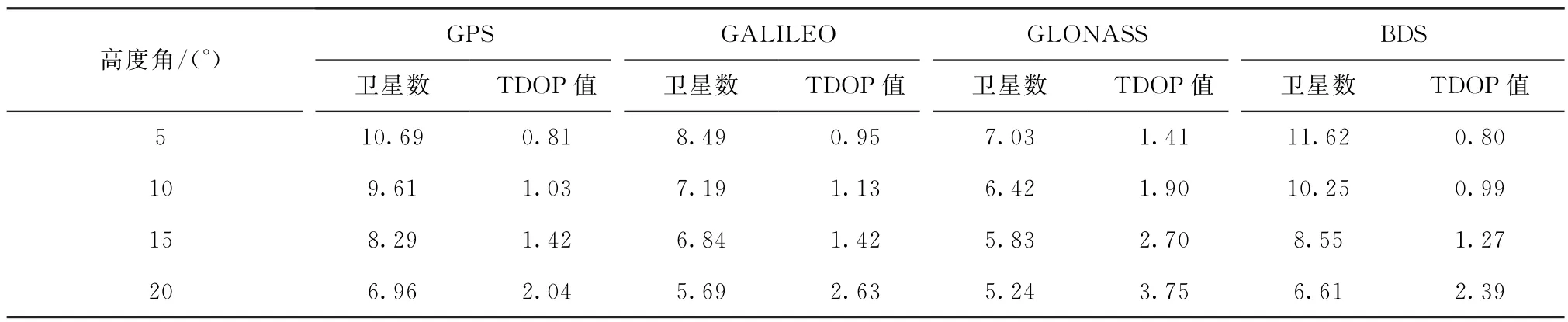
表3 OHI3测站不同系统卫星数、TDOP均值Tab.3 Number of satellites and TDOP mean of different systems at OHI3 station

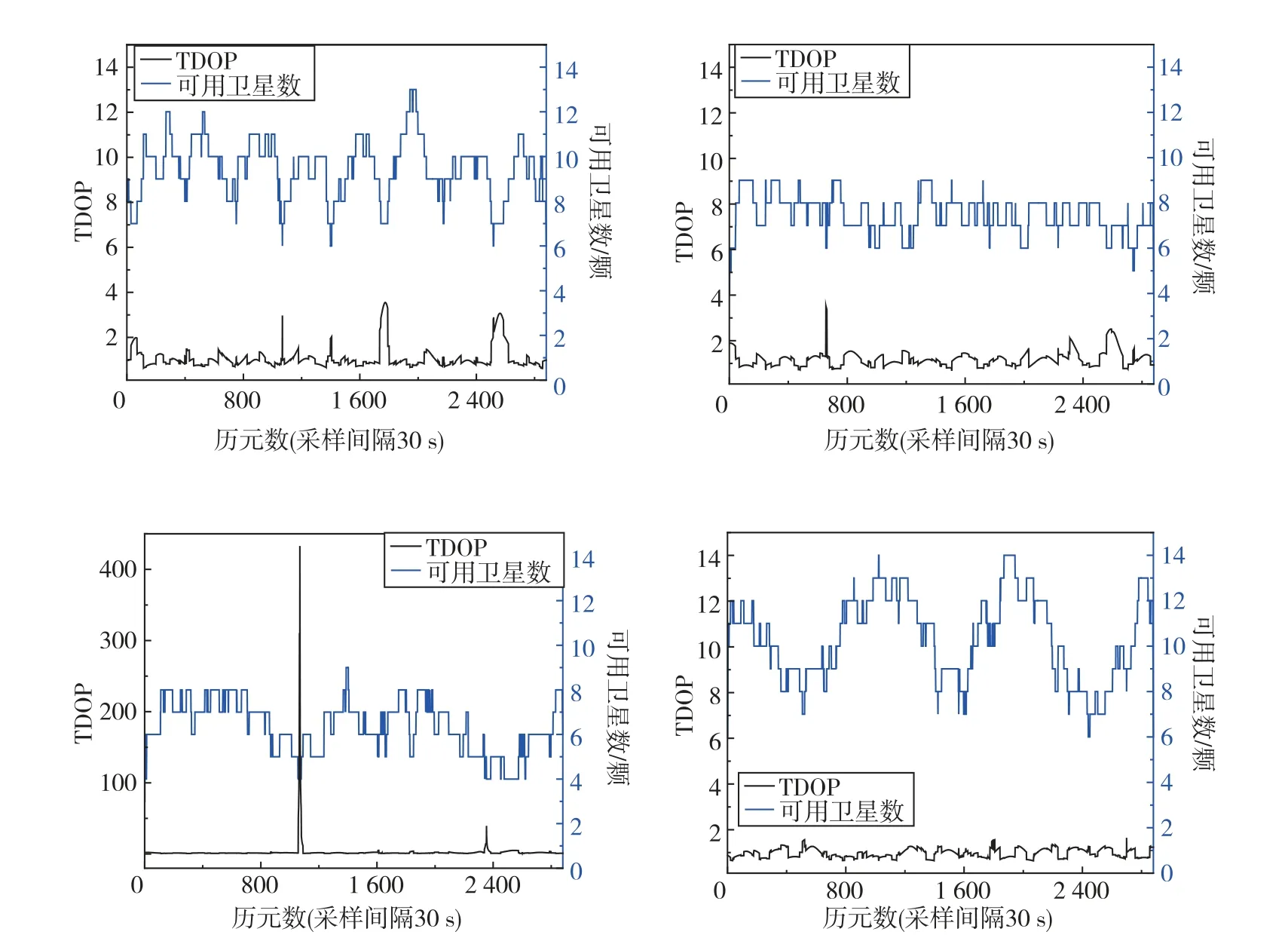
图3 OHI3测站不同系统一天内的卫星数、TDOP值Fig.3 Number of satellites and TDOP values in a day for different systems of OHI3 station

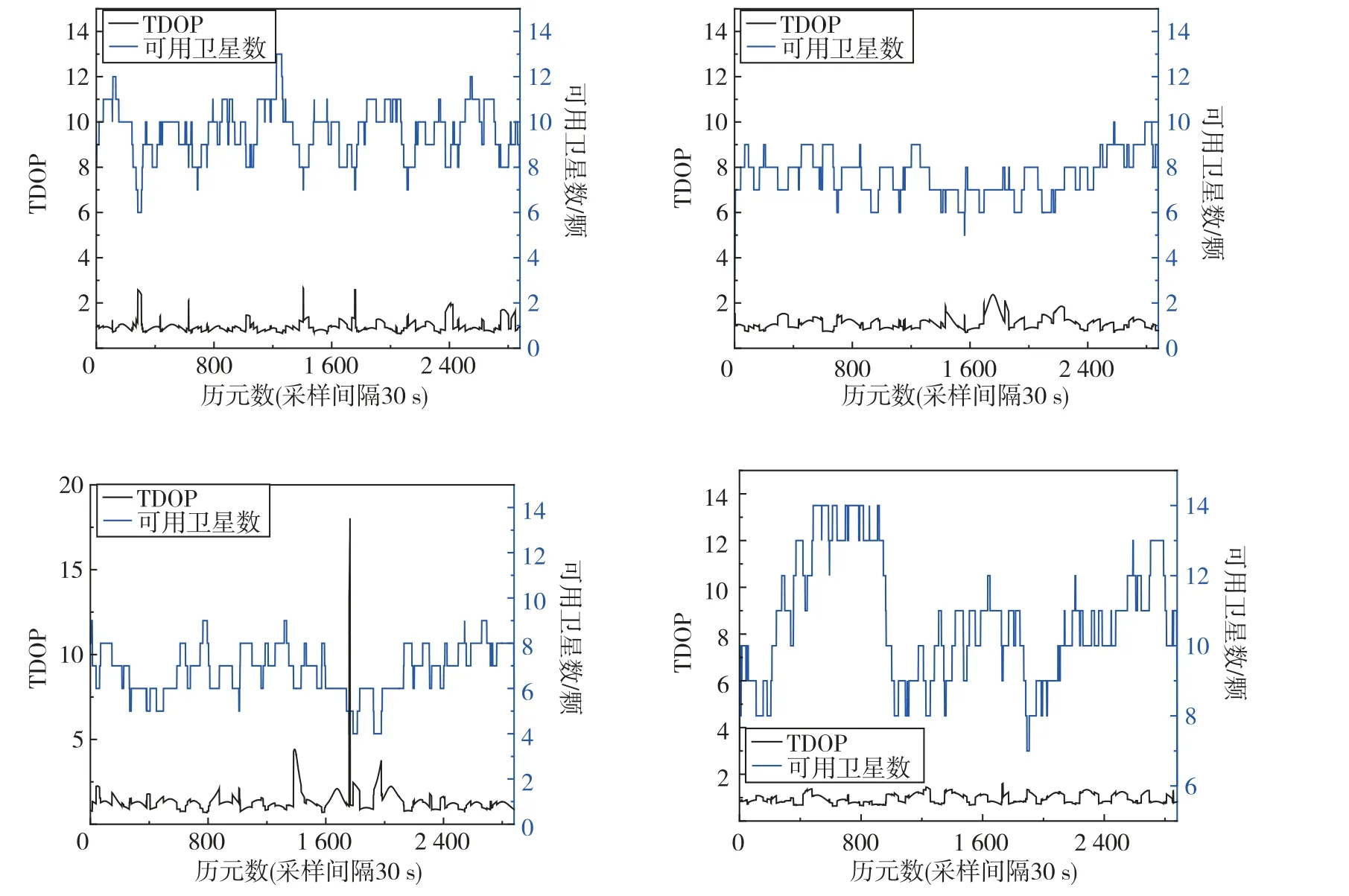
图4 YEL2测站不同系统一天内的卫星数、TDOP值Fig.4 Number of satellites and TDOP values in a day for different systems of YEL2 station

结合表3和表4可以看出,当截止高度角为5°时,卫星几何构型良好。截止高度角从5°升为10°,15°时,TDOP值衰减不大;但当截止高度角升为20°时,测站的TDOP值有较大衰减。

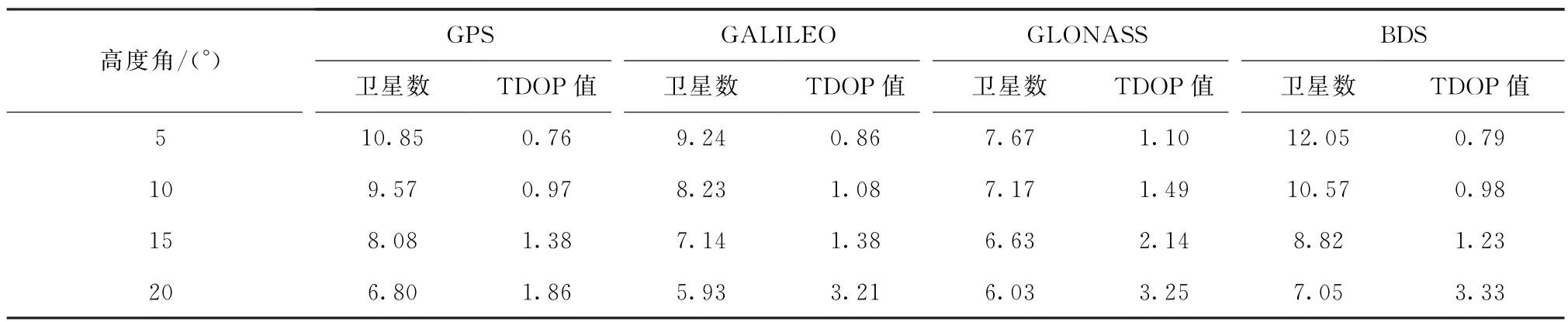
表4 YEL2测站不同系统卫星数、TDOP均值Tab.4 Number of satellites and TDOP mean of different systems at YEL2 station

分析表3和表4可得,对于GPS系统,在OHI3测站,5°,10°,15°和20°截止高度角下平均卫星数分别降低了10.10%,13.74%,16.04%,TDOP 分别衰减了27.16%,37.86%,43.66%。5°,10°,15°和20°截止高度角下YEL2测站的平均卫星数分别降低了11.80%,15.57%,15.84%,TDOP 分别衰减了27.63%,42.27%,34.78%。

结合图3、图4 和表3、表4 可以看出,测站OHI3和YEL2可用卫星数较多时,TDOP值较小,卫星的空间几何构型更好,当提升截止高度角,卫星数降为4～5颗时,TDOP值大幅衰减,此时卫星几何构型较差。在一天内,测站OHI3和YEL2的GPS,GALILEO,BDS系统TDOP 值均相对较小,根据DOP优劣等级标准,为优等,但GLONASS系统的TDOP值某些历元存在较大的跳变,几何构型不太稳定。

4 性能评估

4.1 频率稳定表征方法

Allan方差是常用的频率稳定度的表征方法。为评估PPP时间传递链路的频率稳定度,本文采用Allan方差进行评估。其表达式为

式中:δy(τ)表示计算得出的Allan方差的平方根;τ为采样间隔,τ=nτ0,其中τ0为原始序列采样间隔,其中τ0=30 s;N为观测时间序列的总历元数;i表示第i个历元,Ti为该历元的钟差解;m表示平滑因子。

4.2 卫星导航系统时间传递稳定度对比

GPS,GALILEO,GLONASS,BDS 的PPP 时间传递原理虽基本相似,但因每个系统的信号体制、卫星分布等有所不同,其时间传递性能也有所差异,为从频率稳定度的角度评价PPP时间传递的精度,使用Allan 方差分析OHI3-KOUR,YEL2-KOUR 两条时间传递链路的时差。

图5 给出了不同系统PPP 计算的OHI3-KOUR,YEL2-KOUR 时差的时间序列。可以看出,在不同系统链路时差的时间序列变化比较一致,在YEL2测站GPS,Galileo,BDS系统下的时间序列相比于GLONASS稳定性更好。在OHI3测站,四系统的时差序列稳健性差异不大,各个系统的时间序列变化趋势仍比较一致。

图5 不同GNSS系统求解的时差序列Fig.5 Time difference sequence solved by different GNSSsystems

图6给出了不同系统获取的时间传递链路Allan方差对比情况,由图可以看出,在高纬度地区,不同系统获取的时间传递链路Allan方差曲线趋势基本相似,Galileo稳定度相较于其他系统稳定性更好,GPS和BDS次之,GLONASS表现较不稳定。

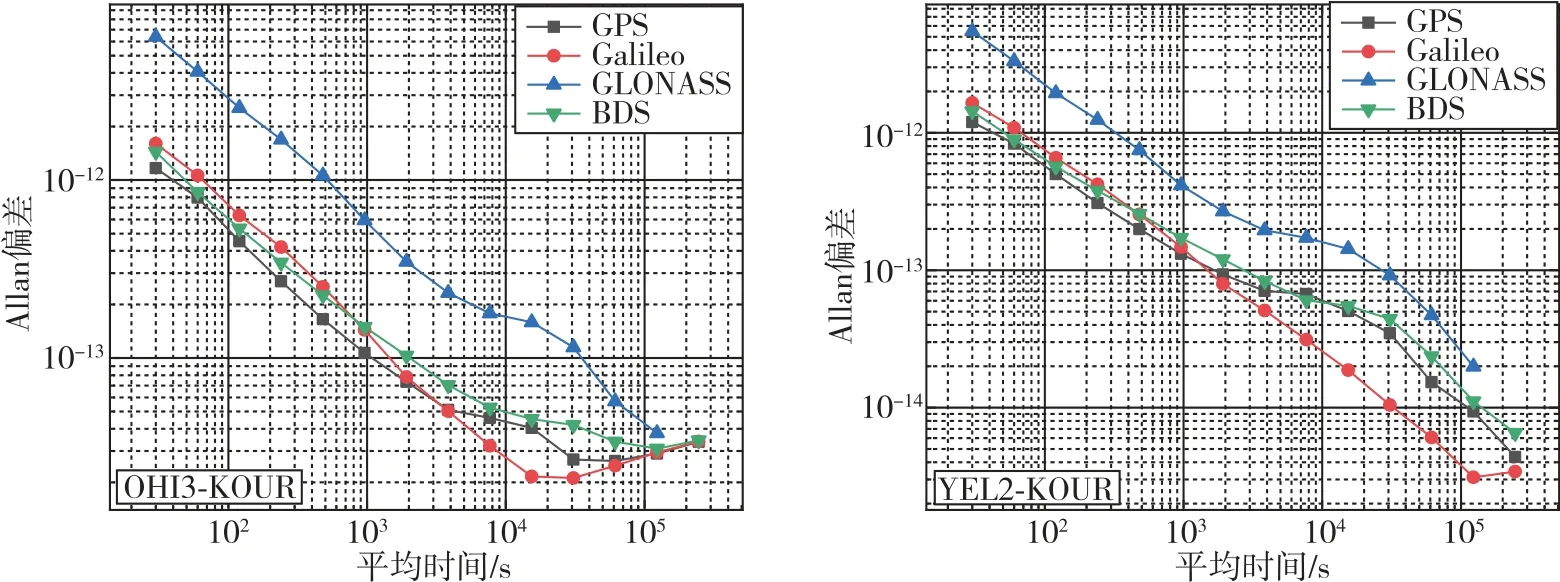
图6 不同系统获取的时间传递链路Allan方差对比Fig.6 Comparison of Allan variances of time transfer links obtained by different systems

结合图5、图6和表3、表4得出,GLONASS系统相较于其他三个系统稳定度较差,这与其较少的可用卫星和卫星间较差的几何构型有一定关系。GPS和Galileo在多系统的高纬度时间链路传递的过程中稳定度相对较好,BDS 的稳定度略差于GPS 和Galileo,GLONASS稳定度最差,其原因是GLONASS系统在卫星观测数及卫星几何构型、卫星钟差和轨道精度、频间偏差(inter frequency bias,IFB)等因素。

4.3 不同截止高度角下稳定性评估

在高纬度地区,卫星与接收机之间的高度角普遍偏低,低高度角对精密时间传递当中的对流层延迟影响较大,降低卫星的截止高度角可以增加观测冗余,提高可视卫星的个数和延长卫星可视时间。但过低的截止高度角又会导致较为严重的多路径效应和大气传播延迟,加大噪声,使观测误差增加,因此本文分析了不同截止高度角下各时间传递链路的稳定性,并分析探讨上述双向作用下的截止卫星高度角的最佳选择。图7和图8分别给出了不同截止高度角条件下不同GNSS 系统获取的OHI3-KOUR,YEL2-KOUR时间传递链路的Allan方差。

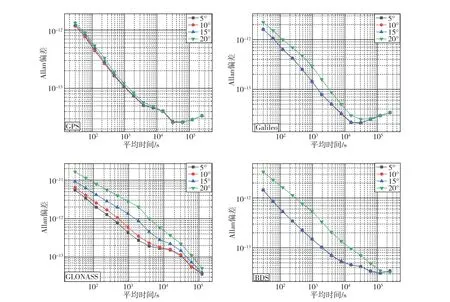
图7 不同截止高度角条件下不同GNSS系统获取的OHI3-KOUR 时间传递链路Allan方差对比Fig.7 Comparison of Allan variance of OHI3-KOUR time transfer link obtained by different GNSS systems under different cutoff altitude angles

由图7 可以看出,在OHI3-KOUR 时间链路中,GPS,Galileo,BDS截止高度角由5°增加至10°、10°增加至15°的过程中,Allan方差随截止高度角的增加并未出现明显变化;Galileo,BDS 系统在截止高度角由15°增加至20°的过程中,稳定性均明显降低。GLONASS 系统在截止高度角由5°增加至10°、10°增加至15°、15°增加至20°的过程中,时间传递链路稳定度均有明显变化,稳定性逐渐降低。

由图8 可以看出,在YEL2-KOUR 时间链路中,不同GNSS系统在截止高度角由5°增加至10°、10°增加至15°的过程中,Allan方差变化与OHI3-KOUR 时间链路相同,但在截止高度角由15°增加至20°的过程中,GPS,Galileo系统稳定度没有明显变化,BDS系统稳定度降低程度相对较小,GLONASS系统的稳定度降低仍相对最大。

结合表3、表4与图7、图8分析可得,在5°截止高度角下,拥有更多的可用卫星数,时间传递的稳定性也更好。当截止高度角由5°增加为10°时,从可用卫星数和TDOP值上看,YEL2测站GPS系统可用卫星数从10.85 降为9.57,平均TDOP 值从0.76衰减至0.97,仍有较多的可用卫星和较为良好的卫星几何构型,因此Allan方差随截止高度角的增加并未出现明显变化。当截止高度角由10°增加至15°时,不同测站上的卫星数目、TDOP值没有发生较大变化,因此不同系统的时间传递链路的稳定性未发生显著变化。当截止高度角增加为20°时,由表3和表4可以看出,平均TDOP值明显升高,部分历元的可用卫星数仅有4颗,几何构型的稳定性很差,因此不同系统的时间传递链路稳定度明显降低。

从截止高度角在15°～20°变化对时间链路稳定性的影响上看,在高纬度地区截止高度角的升高对GPS,Galileo系统的影响较小,对GLONASS,BDS系统的影响较大。但从截止高度角从5°到20°的变化当中,同样对GPS,Galileo 系统的影响较小,对GLONASS系统的影响最大。结合图5和图6中的Allan方差曲线可以得出:在高纬度地区,GPS,Galileo系统的性能相对较好,GLONASS系统的性能相对最差。

从前面的分析可以得出,时间传递链路的稳定性随截止高度角的升高而降低,在高纬度地区进行时间传递时建议选择5°截止高度角。

5 结论

本文研究了GNSS载波相位时间传递理论,选择中低纬度和高纬度地区的典型GNSS 测站进行实验,对其可视卫星数、TDOP 值和不同GNSS 在高纬度地区的时间传递性能进行了分析,得出的主要结论如下:

1)相较于中低纬度地区,高纬度地区测站卫星高度角相对较低,缺少大高度角卫星,但仍然拥有较多的可视卫星,TDOP 值较小,卫星的空间几何构型较好。其中GPS,Galileo,BDS 系统的可用卫星数大多在8～12颗,卫星几何强度也较为稳定。GLONASS 系统部分历元的卫星数仅有4 颗,TDOP值有较大跳变,几何构型相对较差。

2)从不同系统来看,高纬度地区GPS,Galileo,BDS系统的时间传递链路稳定度差异不大,Galileo最优,GLONASS系统的稳定性相对较差。此外,当截止高度角由5°增加为10°和15°时,TDOP值变化不大,因此,链路稳定性变化不大;但增加为20°时,TDOP值衰减明显,其链路稳定性也明显变差。

3)为了拥有更多的可用卫星数,增加卫星几何分布强度,保证更好的时间传递链路稳定度,在高纬度地区进行时间传递时截止高度角建议设置为5°。