工作空间限制下的机械臂路径规划方法∗
2024-01-29储泽楠张修太
赵 凯,储泽楠,张修太
(1.安阳工学院计算机科学与信息工程学院,河南 安阳 455000;2.安阳工学院电子信息与电气工程学院,河南 安阳 455000;3.安阳市异构大数据分析与处理重点实验室,河南 安阳 455000)
随着科技的进步,机械臂作为一种有力的辅助工具,被广泛应用于工业和康复领域[1]。一般情况下,机械臂被安装在固定的底座上,完成固定的工作。然而,随着机械臂可从事的工作越来越多,有些工作内容具有不确定性的,这就对机械臂能否顺利完成该工作提出了要求。每台机械臂因机械设计不同,能够工作的范围也不同。因此,确定机械臂的工作范围非常重要,也非常有助于帮助机械臂完成不确定性的工作,如人机对弈[2]。机械臂的工作范围又称为工作空间或能力地图,很多学者都对其进行了深入的研究。Porges 等[3]对空间机器人的能力地图进行了建模和分析,并对几种特定机械臂的工作空间进行了可视化和存储。对机械臂工作空间的建模包括几何方法、理论分析和数值方法。其中,数值方法因灵活方便,可操作性强,是目前的研究的趋势。蒙特卡洛方法是其中一种较为常用的数值方法。Peidró 等[4]基于高斯增长提出了一种改进的蒙特卡洛方法来获取机器人的工作空间,以改进传统蒙特卡洛方法依靠增加随机点数提高精度的缺点。Chaudhury 等[5]基于蒙特卡洛方法获取固定的工作空间,结合梯度下降方法设计多自由度并行机械臂。其他的众多学者针对工作空间的建模和分析也提出了一些其他的数值方法,如分支修剪技术[6],神经网络技术[7],六维空间划分技术[8],启发式方法[9]等。
工作空间确定以后,就可以进行下一步的工作,如机器人的设计[4]等。Porges 等[10]将建立的机械臂能力地图,用于估计机械手的抓取位姿。Isiah 等[11]根据工作空间分析,解决冗余机械臂的逆运动学闭环求解问题。Vahrenkamp 等[12]则利用工作空间解决机械臂的放置问题。Liu 等[13]则根据关节工作空间的划分,解决机械臂的轨迹规划问题。Zacharias 等[14]采用混合方法建立了工作空间模型,并指出可用于机器人的位置放置和任务规划。然而,正如我们所提到的,机械臂的许多工作并不确定,这将涉及到机械臂末端的移动,即笛卡尔空间的路径规划。很明显,路径点是否可行,不仅仅受到障碍物影响,还会受制于工作空间。针对这个问题,本文提出了一种基于工作空间和障碍物限制的快速搜索随机树(Rapidly-Exploring Random Trees,RRT)的路径规划方法。
1 背景算法
1.1 蒙特卡洛算法
使用蒙特卡洛方法确定机械臂工作空间的思想非常直观,是一种基于采样的方法,可以概括为:
式中:Ω代表机械臂在笛卡尔坐标系下的工作空间;x∈ℝ3代表机械臂末端使用坐标表示的笛卡尔空间位置;q∈ℝn代表n自由度机械臂关节空间中的各关节的值,一般为弧度值;qmin和qmax分别表示关节值的下限和上限;f(•):ℝn→ℝ3表示将关节空间映射到笛卡尔空间的变换,对于机械臂来说,实际上指的就是正向运动学变换。
典型的蒙特卡洛算法有如下2 个步骤:
①获取机械臂各关节的活动范围qmin≤q≤qmax,其中q=[q1,q2,…,qn]∈ℝn。在活动范围内,对每个关节进行随机采样,采样方法如下:
式中:rk是[0,1]上的随机值和分别为第k个关节的下限值和上限值。
②将式(2)随机产生的关节值进行n自由度机械臂正向运动学变换,可以得到笛卡尔空间的机械臂末端位置。
③大量重复步骤①和步骤②,即可得到机械臂的工作空间。
从整个算法过程,很容易知道,该工作空间是以点云的形式存在的。由于随机产生关节向量,蒙特卡洛算法也无法保证生成一个完整的工作空间。因而,要覆盖整个工作空间,随机采样次数应尽可能地多。另外,要完成如路径规划这样的任务,产生的点云数据需要按照一定的方式进行存储。例如,将点云数据分布到边长很小的正方体中,以适应路径规划等任务的需要。这样的分布过程计算量非常大。
1.2 快速搜索随机树(RRT)算法
快速搜索随机树(RRT)算法是一种基于采样的路径规划算法,广泛用于平面、立体以及高维空间的路径产生。给定起始点和目标点,RRT 算法可以快速有效地找到一条无障碍路径[15]。因其算法简单,健壮性强,可适用于多种机器人的路径规划,如导航车,机械臂,轮式机器人等。
因多自由度机械臂末端多在三维空间内活动,在这里,将三维空间中的标准RRT 算法叙述如下:
①构造一棵随机树R,并将起点Ps作为树的第一个节点。
②在笛卡尔空间中进行采样,寻找合适的满足条件的节点Sample。获取Sample 的方法一般使用随机采样,当然也可以应用其他方法,如低差异采样。
③在随机树R上寻找最近节点Pn,满足‖Sample-Pn‖≤‖Sample-Pr‖,其中Pr是任意一个随机树上的节点。最近的度量‖•‖也可以采用多种度量方式,如马氏距离,欧氏距离。
④生成新的随机树节点。给定步长h,产生新的节点
⑤检测新产生的节点Pz与最近节点Pn的连线是否与障碍物重叠。如果重叠,则放弃Pz,返回步骤②;否则将Pz作为新节点加入随机树R中,进入步骤⑥。
⑥检查新节点Pz与终点Pe之间的距离是否满足给定的阈值。如果满足阈值,则路径规划完成;否则,返回步骤②。
RRT 算法虽然不能保证生成的路径是最优的,但寻找速度比较快。标准RRT 算法虽然也采用了随机的采样方法,但采样的位置为整个笛卡尔空间,并不适用于有工作空间限制的多自由度机械臂的末端路径规划。
2 工作空间限制下的RRT 方法
为了使RRT 算法能够适用于带有工作空间限制的多自由度机械臂的末端路径规划,需要为工作空间的生成和存储设计合适的方法,并对RRT 进行改进。
2.1 基本思想
本文提出的工作空间建立方法与蒙特卡洛方法不同,基本思想如图1 所示。将整个空间离散化为许多小正方体,如图1(a)所示。其中任意一个小正方体中包含三个点,A,B,M,其中M为线段的中点,为小正方体任意一条空间对角线,如图1(b)所示。对多自由度机械臂来说,A,B,M三点中任意一点不可达,则该小正方体被标记为不可达空间,反之则为可达,如图1(c)所示。所有可达小正方体就构成了机械臂的能力地图,如图1(d)所示。
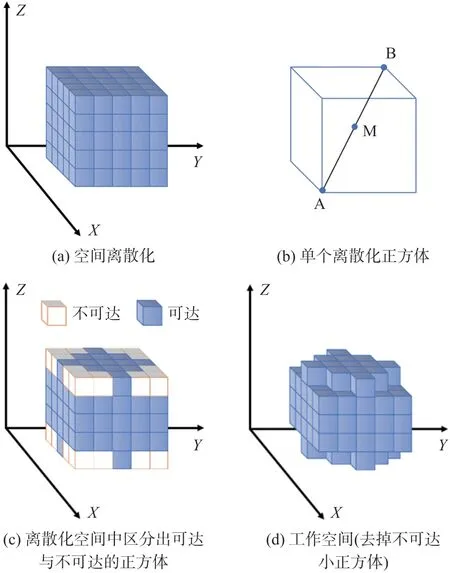
图1 工作空间产生
2.2 算法步骤
具体来说,算法包括非实时部分和实时部分,非实时部分离线完成一次即可,实时部分可支持在线进行路径规划。整个算法的步骤归纳如下:
2.2.1 非实时部分
步骤1:将整个既定空间按照要求离散为小正方体,数量为D。既定空间的获取可以根据机械臂连杆和关节的总长度确定,也可根据工作环境确定。
步骤2:获取所有小正方体顶点序列A={A1,A2,…,AD}和B={B1,B2,…,BD},并获取中点序列
步骤3:对集合A,B,M中的元素进行遍历,求解多自由度机械臂的逆运动学,对于无法获得逆运动学解的元素进行标记。第k小正方体中,Ak、Bk、Mk中任意一点无法求出逆运动学解,则整个小正方体标记为不可达,从工作空间中移除。剩余的所有小正方体就被作为机械臂的工作空间。
步骤4:去掉不可达小正方体后,所有可达小正方体的个数为E。将E个小正方体的顶点和中点构成一个新的集合Ξ={A1,A2,…,AE,B1,B2,…,BE,M1,M2,…,ME},该集合将作为RRT 算法的搜索空间。
2.2.2 实时部分
步骤5:给定起点Ps和终点Pe,检查两点是否在工作空间内。具体做法为遍历集合Ξ,检查Ps和Pe三个坐标值是否落在某个可达小正方体内部。
步骤6:构造一棵随机树R,并将起点Ps加入树中,随机给定Ξ中元素的索引,得到采样值Sample。
步骤7:在随机树R中查找与Sample 的欧氏距离最小的节点Pn。并给定步长h,生成新的随机树节点Pz。
步骤8:检查新节点Pz与Pn的连线是否与障碍物重叠。为保证算法的通用性,对所有障碍物采用球形包络。如果重叠,则放弃Pz,返回步骤6;否则将Pz作为新节点加入随机树R中,进入步骤9。
步骤9:给定阈值ε,失败次数λ,检查终止条件①‖Pe-Pz‖≤ε,②λ≤20 000。如果两个条件均满足,则路径已经找到;如果仅满足条件②则转入步骤7 继续查找;如果不满足条件②则路径寻找失败。
3 实验及分析
为验证算法的有效性,利用机器人工具箱[16]中的机械臂对算法进行了测试。该机械臂为PUMA560,有6 个自由度。为方便对比,本文还实现了蒙特卡洛算法和标准的RRT 算法。
如图2(a)所示,蒙特卡洛算法对每个关节随机采样,使用正向运动学求解后,得到了共27 000 点的点云数据,为了方便观察和对比,图2(b)给出了整个工作空间在XY平面上的投影,是一个近似的圆环形状。周围的空白区域是由于机械臂本身的限制导致不可达区域,中间的空白区域是机械臂基座的放置位置,因距离基座和本体太近而不可达。
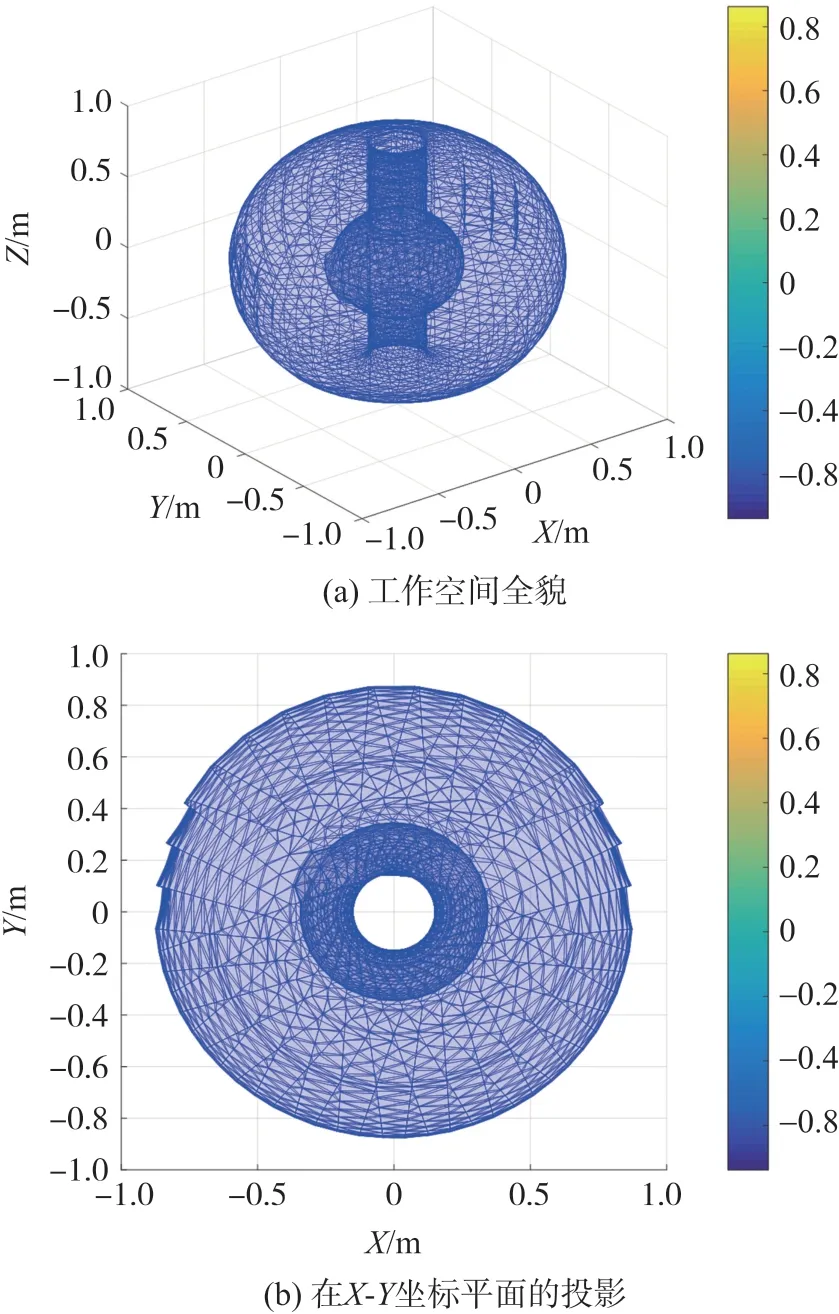
图2 蒙特卡洛算法产生的工作空间
在执行本文提出方法的实验中,环境空间假定为长宽高均2 m 的大正方体,设定离散化的小正方体的棱长为0.1 m,如图3(a)所示。如果想获取更高的精度,可减小小正方体的棱长。通过求解逆运动学,将不可达的小正方体去除,得到图3(b)所示的工作空间。为了方便对比,将工作空间投影到XY平面上,如图3(c)所示。
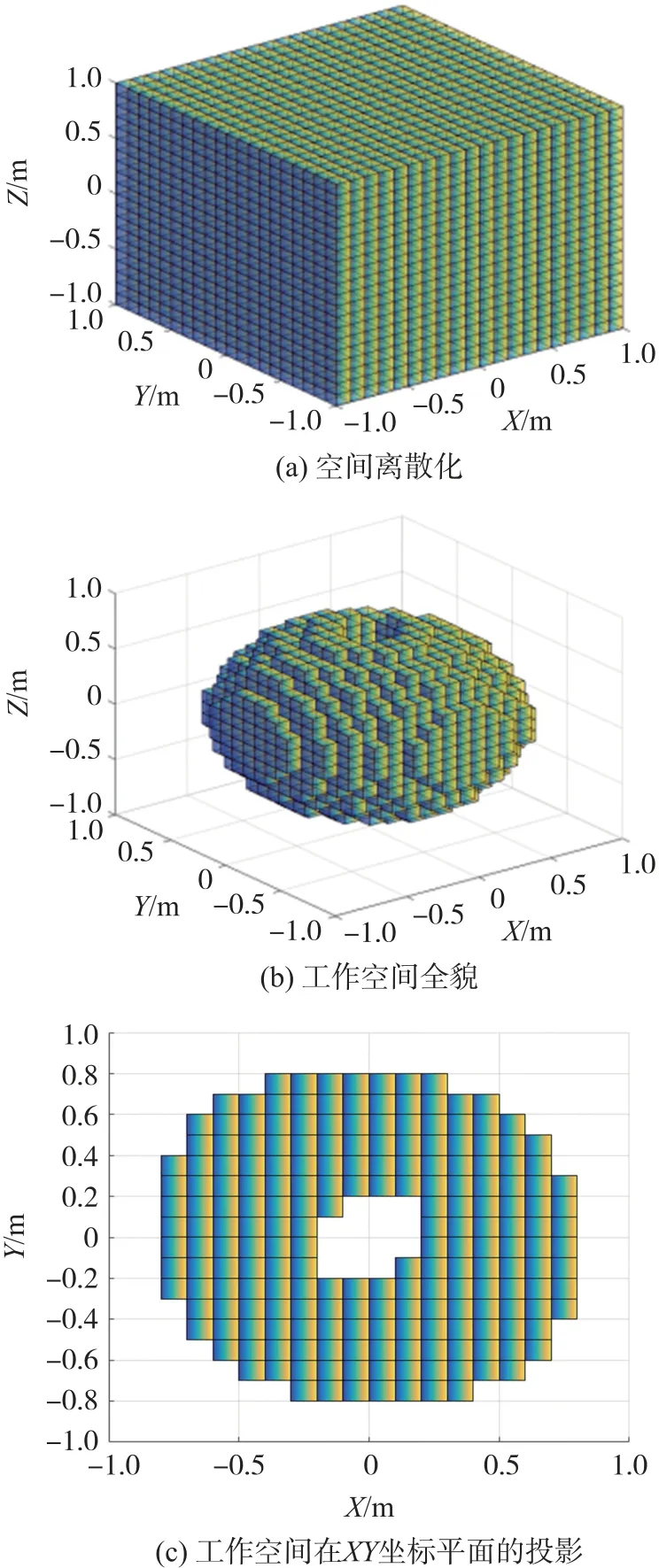
图3 本文方法生成的工作空间
对比图2(b)和图3(c),可以看出,在XY平面上的投影相差不大,造成差别的主要原因是本文的方法使用的基本元素是小正方体,而蒙特卡洛算法使用的是点云数据。严格来说,蒙特卡洛算法的精度更高,但计算成本偏高,而且点云格式的数据也不适合接下来的基于采样的路径避障和规划算法。
有了工作空间后,就可以执行路径的实时规划。为了公平对比,两种搜索算法的步长h均设定为0.05 m,新节点与终点之间的阈值ε也均设置为0.05 m。如图4(a)所示,本文所提出的基于工作空间限制的RRT 算法的搜索空间,实际是所有小正方体的顶点和中点的集合Ξ,这将最大限度地确保搜索的采样值和新节点都在工作空间内部。标准的RRT 算法的搜索空间是一个棱长为2 的空间正六面体,因而观察图4(b),搜索的节点很多都超出了工作空间的范围,甚至有的节点超出了设定的整个环境空间。
4 结论
本文为完成多自由度机械臂末端的路径规划任务,考虑机械臂工作空间的限制,提出了一种带有工作空间限制的RRT 算法。在产生工作空间时,首先将整个工作环境进行离散,然后使用逆运动求解确定工作空间。这种方法所确定的工作空间可以很容易地应用采样型的路径规划算法,如RRT 等。通过实验对比,我们发现这种方法与蒙特卡洛算法产生的工作空间相差不大,但计算量小,且在路径规划时能有效避免搜索到的节点超出工作空间,确保机械臂路径规划的成功。
