一种粒子群算法在语音识别中的应用∗

胡宏梅，别玉霞

(1.苏州健雄职业技术学院人工智能学院，江苏 太仓 215411；2.沈阳航空航天大学电子信息工程学院，辽宁 沈阳 110136)

1 粒子群算法的基本原理

粒子群优化算法(Particle Swarm Optimization，PSO)是Kennedy 和Eberhart 受鸟群觅食的启发而提出来的一种算法，将鸟群作为PSO 算法中的种群，每一只鸟相当于PSO 算法中一个粒子，鸟的觅食过程看作为粒子迭代进化过程，将鸟觅到的食物看作为PSO 算法欲求解问题的目标，找到食物的鸟即为所有粒子所追随的对象，即最优解。PSO 算法模拟鸟之间的个性化学习和彼此协作交互，促使整个群体不断搜索并向最优解靠近，常用来解决一些优化问题。

PSO 算法初始化为一群随机粒子，而每个粒子对应到优化问题中都会得到一个适应值，同时，粒子的移动是通过不断更新速度和位置完成的，而这两个参数的更新是由当前的最优粒子和个体最优值来决定的，通过跟踪这两个极值从而达到搜索最优解的目的。

假设欲求解问题的目标函数为:

记群体中粒子i的位置Xi＝(xi1，xi2，…，xin)，速度Vi＝(vi1，vi2，…，vin)，且该粒子所经历的最好位置记为Pi＝(pi1，pi2，…，pin)，整个群里所经历过的最好位置记为Pg＝(pg1，pg2，…，pgn)，则在跟踪两个极值移动过程中，该粒子第t＋1 次迭代中速度和位置更新如式(2)所示:

式中:c1、c2为学习因子，也称为加速常数；r1、r2是在(0，1)之间产生的随机数；w为惯性权重；vij(t＋1)为粒子i在第t＋1 次迭代中第j维速度，vij∈[－vmax，vmax]，其中，vmax是常数，用来限定粒子的飞行速度。

速度更新公式中，包括了三个部分，第一部分是粒子i的惯性部分，反映出了粒子i的运动习惯，使其维持之前的运动速度，保证算法的全局搜索性；第二部分是认知部分，让粒子i能记住自己所经历过的最好位置，并向其不断逼近的趋势，具有一定的目标性，防止随机搜索而偏离最优解；第三部分为社会部分，反映出粒子之间的协同合作性，使得粒子在保持自身移动的同时还能关注全局最优值，并向其移动靠近，进而能达到搜索全局最优的目的。

粒子i所经历过的最好位置Pi是由式(3)确定:

而整个群体所经历过的最好位置Pg(t)由式(4)决定:

PSO 算法的基本流程如下:

步骤1 初始化种群大小为M，维数为n及参数c1、c2、r1、r2。

步骤2 初始化M个粒子的速度V＝{V1，V2，…，VM}和位置X＝{X1，X2，…，XM}。

步骤3 计算每个粒子所对应的目标函数f(Xi(t))，并根据式(3)和式(4)更新个体最优Pi和全局最优Pg。

步骤4 根据式(2)更新粒子的速度Vi(t)和位置Xi(t)。

步骤5 是否达到最大迭代次数或最大阈值，如果是，则结束算法，输出全局最优解；如果否，则跳到步骤3 继续执行。

2 粒子群算法中参数分析

PSO 算法中主要涉及到的参数有:学习因子c1、c2，惯性权重w以及最大速度等。

2.1 惯性权重的设置[1]

惯性权重w是PSO 算法中比较重要的参数之一，它的大小决定了本次迭代中粒子飞行速度受上次迭代中飞行速度影响的程度，也间接决定了粒子全局和局部的搜索能力。

分析可知，w取较大值有利于全局搜索，但增大算法开销，降低算法效率；w取较小值有利于局部搜索，加速算法收敛，但容易陷入局部最优，因此设置一个合适的w即可平衡全局和局部搜索能力，兼顾算法收敛速度和收敛精度，降低陷入局部最优解的可能性，提高算法的整体性能。

Shi 等[2]通过一系列的实验，得出惯性权重函数的线性下降范围为[0.9，0.4]，惯性权重范围的确定使得粒子在搜索的前期能够迅速明确最优解所处的搜索范围。根据惯性权重的变化，粒子的搜索速度和范围也随之变化，从而实现更加精确的搜索。但这种方法存在一个问题，即若粒子前期未能搜索到最优位置，则后期随着粒子全局搜索能力的下降，局部搜索能力的增强，则容易出现局部收敛，针对这一现象，提出了一种非线性惯性权重算法[3]，其表示为

式中:wstart和wend分别为惯性权重的起始值和终点值，即最大值和最小值，k为控制因子，控制着惯性权重随迭代次数的变化，文献中指出k的取值为3.0～4.0 时，算法所达到的效果较好。

如图1 所示，当迭代次数在0 到200 之间时，惯性权重w从慢到快变化；而当迭代次数在250 以上时，惯性权重w由快到慢变化，故粒子在搜索前期无法保持较大的搜索范围，后期的收敛速度也受到一定的影响，同时，两者惯性权重的交接点即0.675也处于这个范围内，故在惯性权重近于交接点值时，可以通过增加迭代次数来扩大粒子的搜索范围。

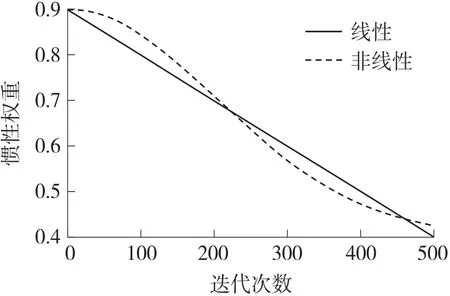
图1 线性和非线性惯性权重函数曲线

如图2 所示，可以看出k的取值不同，惯性权重的结果也会受到影响，k＝0.5、1.5、3 和3.6 时，对应的惯性权重如图2 所示，当k＝0.5 时，惯性权重取值较大，搜索范围较为广泛，不易搜索到最优解；当k＝1.5 时，惯性权重取值的前期变化较为缓慢，能够获得较大的搜索范围，而后期惯性权重相对于k＝3 和3.6 时，减小得较为缓慢，很难在局部搜索中获取最优解。为了确保粒子在整个迭代过程中既能有效地进行全局搜索，又能有效进行局部搜索，让粒子在前期能更精确获得最优解搜索范围，后期能获得最优解，本文将采用非线性和线性相结合的方式来设置惯性权重，如式(7)所示:

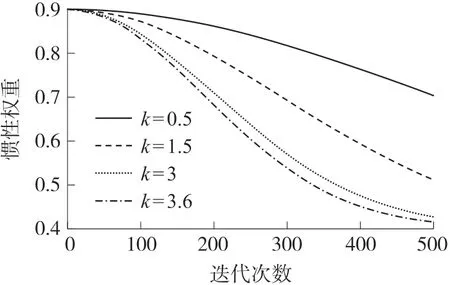
图2 k 取值不同时惯性权重的对比

2.2 学习因子的设置

学习因子c1使得粒子根据个体的历史经验向个体最优解靠近，而c2则使得粒子通过个体间的相互协作引导着粒子向全局最优方向靠近。

当c1＝0、c2＝0 时，粒子只靠自身速度在进行盲目搜索；当c1≠0、c2＝0 时，粒子将失去与其他粒子间的协作关系，仅靠自身能力搜索整个空间，缺乏搜索指导，其他粒子的优势将无法体现，易陷入局部收敛；当c1＝0、c2≠0 时，粒子的搜索主要依靠与其他个体间的相互协作，而缺少了对自身经历的学习，盲目跟随群体中的最优粒子，易错过最优解。因此，只有对c1、c2进行合理取值，才能使得粒子充分利用自身经验和个体间协作有效搜索全局最优解。

本文以线性权重和非线性权重的交接点约为0.675 为分界点，当w大于等于交点时，则学习因子c1和c2分别取2.5 和0.5，而w小于交点时，学习因子c1和c2分别取0.5 和2.5，具体如式(8)所示:

2.3 最大速度vmax的设置

粒子群里的粒子速度主要是用来控制粒子在搜索空间中的移动距离。通常，粒子速度越大，其每次搜索跨越度就越大，全局搜索能力就越强。但如果粒子最大速度设置过大，在提高其全局搜索能力的同时也提高了粒子的自由度，这样容易使粒子跳过最优解，很难搜索到全局最优；反之，如果粒子最大速度设置过小，每次迭代粒子在空间中移动就相对缓慢，局部搜索能力增强，全局搜索能力变弱，粒子容易陷入局部最优。vmax的选择通常凭经验给定，并一般设定为问题空间的10%～20%。

3 粒子群算法的应用

3.1 语音识别原理[4－6]

如图3 所示，首先将语音信号分成训练语音和识别语音，然后进行预处理和特征参数提取，得到两组随机向量序列；接着通过矢量量化器把两组随机向量序列转化成两组观测序列，一组用于训练DHMM 模型，一组用于识别，最后利用Viterbi 算法计算测试观测序列在每个DHMM 上的输出概率，输出概率最大的词就是识别结果。而本文所做工作对应的是图3 识别过程中矢量量化里的码书设计。

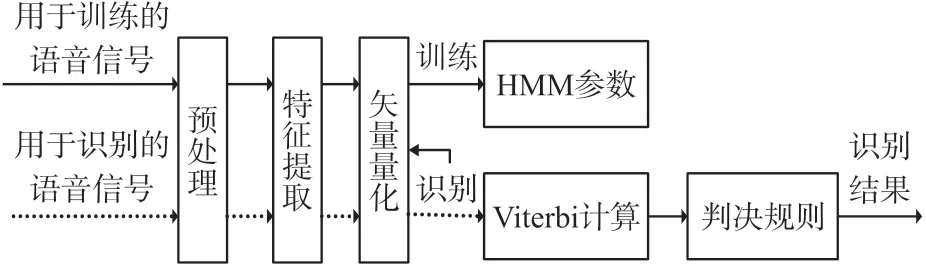
图3 语音识别方法

3.2 编码方式

从一段语音中提取M个特征矢量作为矢量量化码书设计的训练矢量，其维数为k，而码书大小为N。粒子群算法采用的是基于码书的编码方式，每个编码和可行解相互对应，每个粒子对应一个码书，即每个粒子对应具有N个码字的码书。在这种编码方式下，每个粒子都是由N个聚类中心(码字)组成，故每个粒子的速度Vi和Xi位置都是N×k维矢量，均可表示为:

3.3 初始粒子的设置

数据维数为k，给定n个粒子，最大迭代次数为Tmax。最初将训练矢量任意归类，随后将采用最近邻条件和质心条件获取初始粒子。初始化中，粒子i的位置矢量即为矢量量化码书的胞腔质心，其速度矢量可随机初始化为0，按照此过程循环n次，即可产生n个粒子速度和位置矢量。

3.4 适应度函数

在矢量量化码书设计中，通常采用类内、类间离散度以及矢量不均匀来衡量码书设计算法的性能，本文采用类内离散度的倒数作为适应度函数。设训练矢量为Z＝{z1，z2，z3，…，zM}，利用适应度函数确定最佳划分，将训练矢量聚类到每个胞腔中形成最终码书为Y＝{y1，y2，y3，…，yN}。式(11)给出了类内离散度J的求解方法:

式中:d(zi，yj)为胞腔i内所有训练矢量到其质心的距离，ziεRj表示胞腔j内的所有训练矢量。

类间离散度是指码书中各胞腔质心间的距离，其值越大，说明收敛性能越好，码书质量越高，其计算公式如式(13)所示:

式中:yi和yj分别是指第i、j胞腔的质心，T为转置。

适应度函数采用类内离散度的倒数表示，用f表示，如式(14)所示，c为一个调节常数。由适应度函数可知，类内离散度越小，则适应度值越大，码书质量性能越好。

3.5 优化粒子群算法的应用[7－11]

为了避免算法陷入局部最优及过早收敛等问题，本文将引入柯西变异策略以改进算法的收敛速度和收敛精度等问题。

柯西变异公式如式(15)所示，其中CM 为柯西变异算子，rand 为均匀分布在(0，1)范围内的任意实数。

若粒子的种群规模为N，f()代表第t次迭代中第i个粒子的适应度表示第t次迭代中粒子群适应度的平均值，根据式(15)计算粒子群的聚集度δ，当f()距离偏差越大时，δ值越大，说明群多样性越好；当f()距离偏差越小时，δ值则越小，说明群多样性越差。

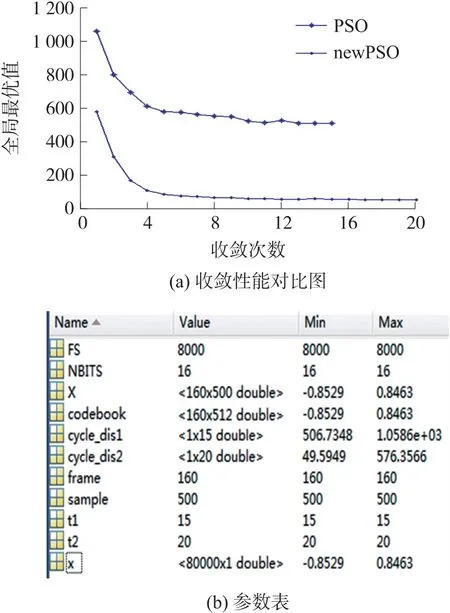
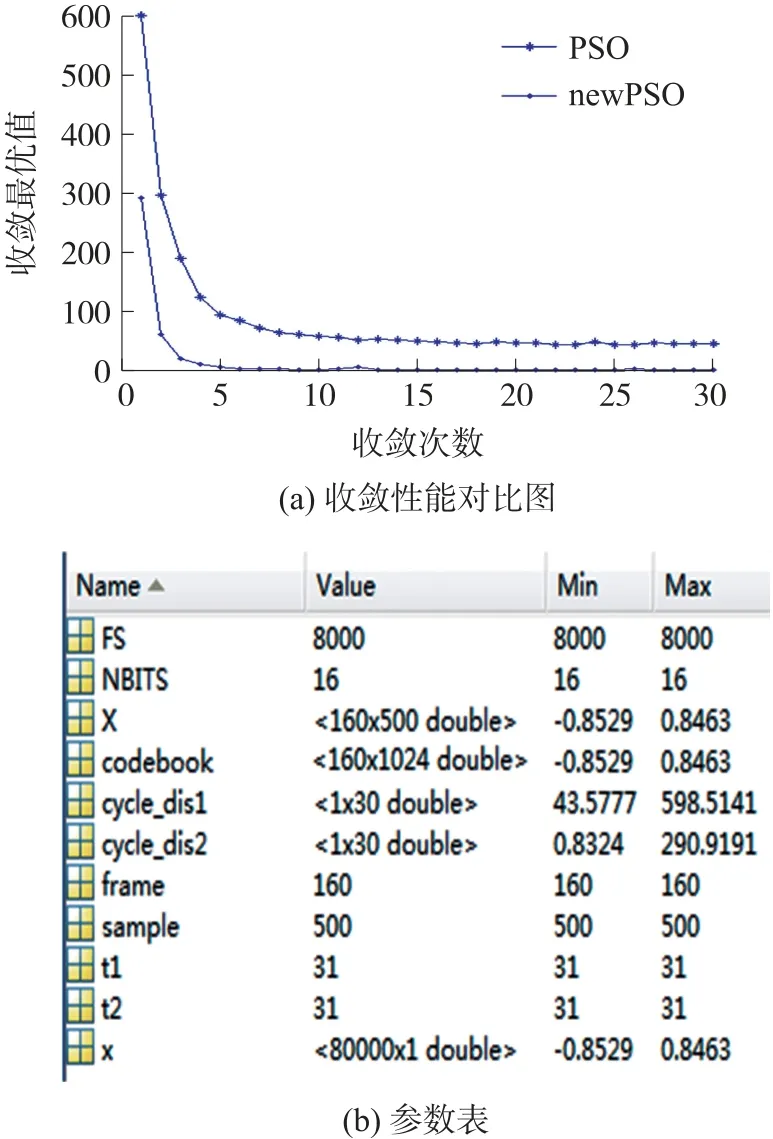
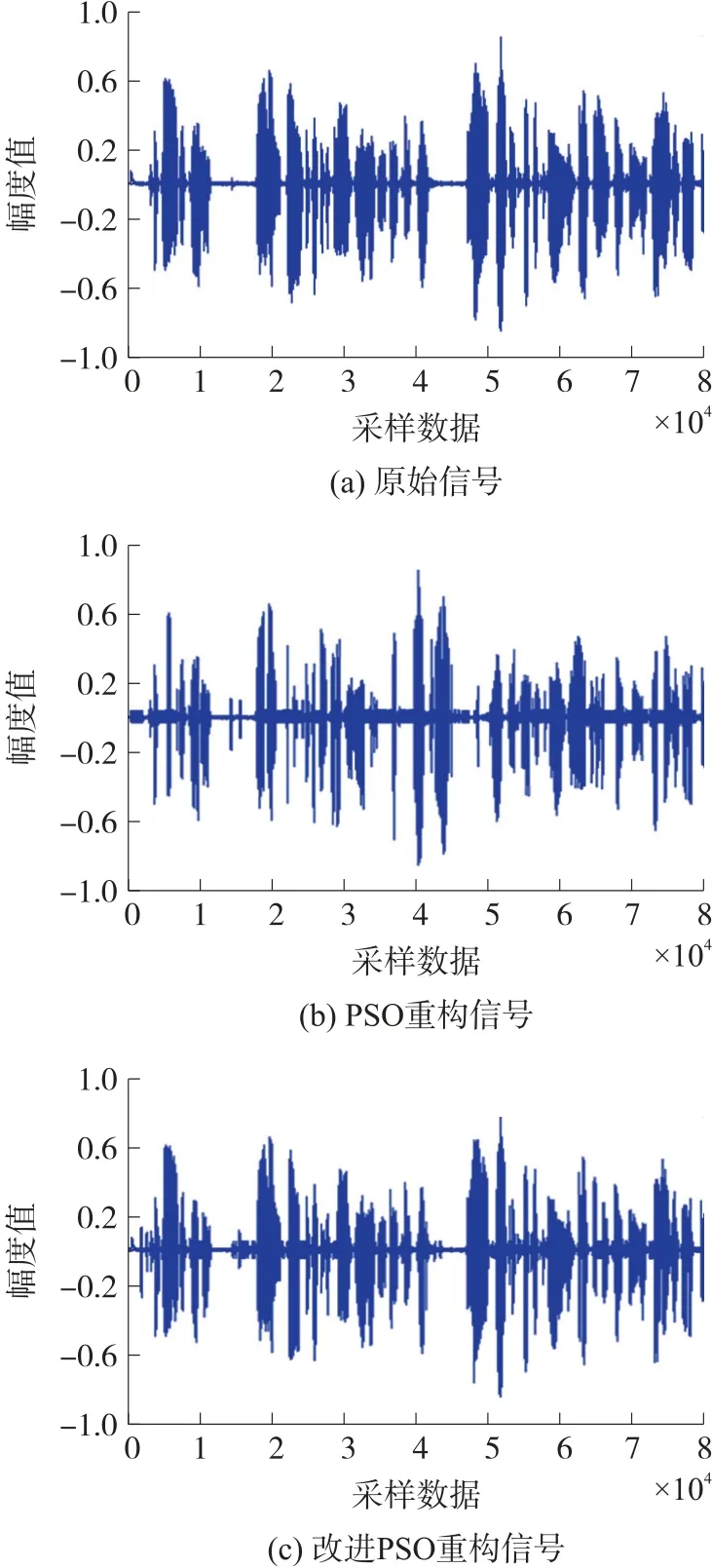
当δ

步骤1 算法初始化。从一段语音中按要求提取M个训练矢量Z＝{z1，z2，z3，…，zM}，其中，zi为k维矢量。将其随机划分聚类，得到初始码书，每个码书有N个码字，将此步骤循环L次，生成L个初始码书，作为粒子群中L个粒子的初始位置X＝{x1，x2，x3，…，xL}，粒子的初始速度V＝{v1，v2，v3，…，vL}、个体极值Pi和全局极值Pg设置为0。

步骤2 参照式(1)和式(2)更新粒子速度和位置，计算并比较其适应值，记录下此次循环中所有粒子经历的最好位置及其适应值，与全局极值Pg相比较，若适应度小于Pg时的适应度，则更新全局极值Pg；同时，记录此次循环中每个粒子所经历的最好位置及其适应值，将其与自身个体极值Pi相比较，若适应值小于自身Pi所对应的适应值，则更新该粒子的个体极值Pi，更新公式参照式(3)和式(4)。

步骤3 计算粒子群的聚集度δ和柯西变异算子CM，比较两者大小，当δ

步骤4 根据最近邻划分原则，以粒子的更新位置为质心，重新将训练矢量进行划分聚类。聚类完成后，根据聚类结果更新确定新的质心，形成新的码书，计算类间离散度。

步骤5 当算法达到最大迭代次数或最大阈值要求时，算法结束，比较类间离散度，输出最优码书，否则，t＝t＋1，转到步骤2。

4 实验结果

本文在MATLAB 平台上运行，选取一段长60 s的语音信号，其中选取40 s 语音作为训练信号，20 s语音作为测试信号，采样频率FS 为8000 次/s，采样精度NBITS 为16 位精度的采样，帧长frame 为160，采样点sample 为500。

算法中的参数选取源于经验值，粒子数N＝30，c1、c2取值见式(8)，惯性权重w的选取依据式(7)，wmax取为0.9，wmin取为0.4。本文将从收敛性和重构信号两个方面对比两种算法的不同。

如图4 和图5 所示，收敛性对比:在codebook 为512 时，迭代次数为20，此时，标准PSO 出现了过早收敛现象，且全局最优值(距离)取值很大，收敛最小值为506.734 8，未达到收敛要求，而改进后的PSO 在迭代次数＝20 时依然在遍历搜索，未完成收敛，全局最优值(距离)取值最小为49.594 9；在codebook 为1 024 时，迭代次数为31，两个算法均呈现逐步收敛，但标准PSO 收敛最小值为43.577 7，而改进后的PSO 收敛最小值却达到了0.832 4，接近原始信号提取的特征值。

图4 codebook＝512 时

图5 codebook＝1 024 时

重构信号对比:通过标准PSO 和改进后的PSO两个算法对原始信号进行量化重构，重构后的信号波形如图6 所示，标准PSO 重构后的信号相对于原始信号丢了部分数据，改进后的PSO 重构后的信号虽然出现了杂波，但整体信号特征保留，同时，通过人的听觉感知两个信号的不同，标准PSO 重构后的信号丢失了部分信息，导致听起来边界不清，内容不易理解，而改进后的PSO 重构后的信号虽出现“吱吱啦啦”的声音，但语音内容容易理解。

图6 语音信号重构对比

5 结论

粒子群优化算法是受鸟群觅食的启发而提出的一种群智能优化算法，常被用于解决多目标优化问题。本文将粒子群算法用于语音信号识别中，为了提升信号识别质量，提出一种柯西变异和粒子群聚集度混合扰动方法改进标准粒子群算法，实现当粒子群聚集度小于柯西变异算子时，则认为此时粒子群多样性欠缺，通过变异当局最优值扰动粒子聚类，避免粒子的过早收敛，增加全局遍历性，实验结果从两个方面验证了改进粒子群算法的性能，证明了其有效性和改善度。