新型双驱动足压电电机非线性接触模型及其实验研究∗
2024-01-29毕卫鹏范平清张江桥付道阔
毕卫鹏,范平清,张江桥,付道阔
(上海工程技术大学机械与汽车工程学院,上海 201620)
压电电机是利用压电元件的逆压电效应将电能转化成机械能的一种驱动装置[1-2]。由于其精度高、功率密度大、断电自锁、无电磁干扰等优点成为一种很有前途的微型致动器,已经在机器人关节、超精密加工、医疗器械、高精度平台等领域得到广泛的应用[3-4]。压电电机根据驱动足的数目可分为单足和多足。单足压电电机定子仅有一个驱动足;多足压电电机定子有两个以上驱动足,一个运动周期可以完成对动子的多次驱动,压电电机能量密度高,输出性能好,成为压电电机新的研究热点[5-6]。
压电电机是通过定/动子的接触摩擦实现宏观运动的,要提高其输出推力和传递效率,必需深入研究定/动子之间的接触摩擦能量传递机理。目前研究人员提出很多建模方法去分析电机定/动子的接触关系,主要分为等效电路法、有限元法和解析法三类。等效电路法[7]比较方便,但是在求解法向接触力和切向摩擦力时不够准确。有限元法[8]在压电电机的设计中有很大优势,可用于复杂结构的分析,但定/动子接触表面的滑移、分离、冲击等复杂接触现象不能准确模拟,而且计算量大。压电电机是一个复杂的机电耦合系统,采用能量法建立其非线性接触解析模型是解决这一问题的有效途径。
Tsai 等[9]利用模态能量法和库伦摩擦模型,通过弹簧模型模拟定/动子之间的法向力,建立了驻波直线压电电机的接触模型,分析了电机瞬态和稳定的响应。Shi 等[10]利用冲量守恒原理建立了压电电机的非线性接触模型。Wang 等[11]对驻波直线压电电机的冲击过程进行了理论和实验研究,分析了能量损耗。Li 等[12]利用等效弹簧模型研究了电机定子与动子之间粘着-滑移-分离等复杂接触关系,分析了接触时间和电弹性对电机输出性能的影响。He 等[13]利用有限元和Rayleigh-Ritz 假设模态法建立了混合仿真模型,定子与动子之间接触简化为面-点接触模型,详细描述了定/动子的黏滑接触过程。上述接触模型是针对单足压电电机的分析,并不适用与双足压电电机,无法分析一个周期中两个驱动足对动子交替驱动的复杂过程。
本文以一个新型的双驱动足压电电机为研究对象,建立该电机的非线性摩擦接触模型。考虑定/动子预压力接触变形,建立动定子非线性法向和切向接触模型,得到压电电机的输出特性模型,并进行实验验证。
1 新型双足压电电机工作原理
为了提高压电电机的输出性能,本文提出一种新型的纵弯耦合双驱动足直线压电电机,如图1 所示。金属弹性体上下共粘贴四片压电陶瓷,分为A和B 两组,压电陶瓷外表面镀银都为正极。A 组压电陶瓷施加sin(ωt)电压激励信号,B 组压电陶瓷施加sin(ωt+π/2)电压激励信号。通过相位差为π/2的两相激励信号,激发电机定子一阶纵振和二阶弯振的耦合振动,使驱动足末端产生椭圆运动,从而驱动动子运动。切换激励信号相位差,可以实现压电电机的反向运动。压电电机在一个运动周期内的工作状态如图2 所示。

图1 压电电机结构图
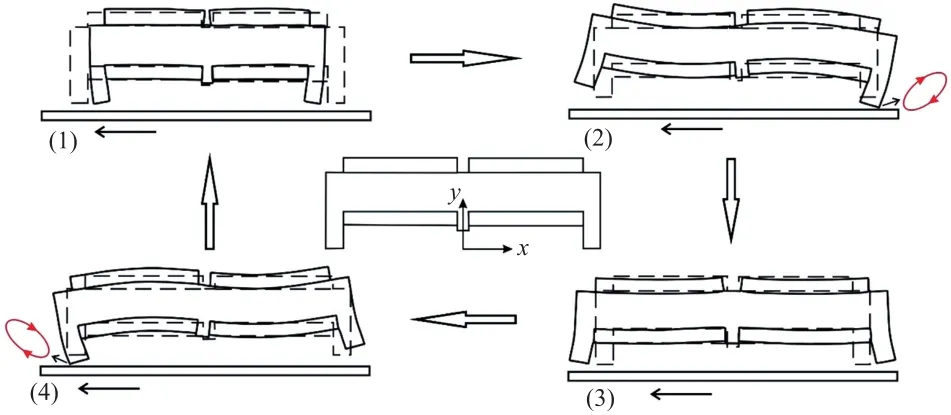
图2 压电电机一个周期的运动状态
当定子从状态(1)运行到状态(2)时,左驱动足抬起,右驱动足接触滑轨驱动动子运动;定子从状态(2)运行到状态(3)时,左右驱动足都脱离滑轨,不产生驱动作用;定子从(3)运行到状态(4)时,左驱动足接触滑轨驱动动子运动;定子从状态(4)运行到状态(1)时,左右驱动足又都脱离滑轨,不产生驱动作用。该压电电机在一个周期内,实现对动子的两次驱动,提高电机的有效做功,改善其输出性能。
2 双足压电电机接触界面模型的建立
2.1 接触模型的建立和分析
驻波压电电机在工作中,动/定子摩擦过程存在间歇分离、粘着、滑移等复杂接触关系,建立准确的接触模型,是揭示定/动子摩擦能量传递机理的关键。当给压电电机施加相位差为π/2 的两个高频正弦电压时,定子驱动足的切向和法向高频微幅振动位移响应可分别表述为:
式中:W为驱动足切向振幅,U为法向振幅。
动子表面层比定子驱动足表面的刚度小,因此预压力作用会导致动子表面发生接触形变。将定/动子的接触层,采用分布式线弹簧进行描述[14]。在预压力作用下,定/动子接触下的中间接触层变形量为ε。在电压激励和预压力的同时作用下,定子的二阶弯振被激发,产生法向振动。中间接触层的变形量随着法向振动的变化而变化,即变形量可表示为法向振动位移与预压力导致的动子接触形变差值w-ε(w=Wsinωt)。设动子和定子接触层的等效刚度为kf。在一个驱动周期内,动子和定子的法向动态接触力FN为:
式中:FP为预压力,kf为等效接触刚度为动子弹性模量,Af驱动足接触面积)。
对于双足压电电机,假设两个驱动足承受均等的预压力载荷,两驱动足的法向振动位移空间相位差为π,因此,在一个周期内交替驱动动子时,法向动态接触力FN可表达为:
当法向动态接触力FN>0 时,定/动子处于接触状态,当法向动态接触力FN<0 时,定动子处于分离状态。因此,在t1~t2和两个接触时间段,动态接触法向力FN都为正值。由于双足共同承担预压力FP,因此,预压力导致的接触形变ε为:
式中:ϕb(L1)为二阶弯振的振型,L1为定子长度,Kb为二阶弯振等效刚度,ηN为法向力载荷系数。
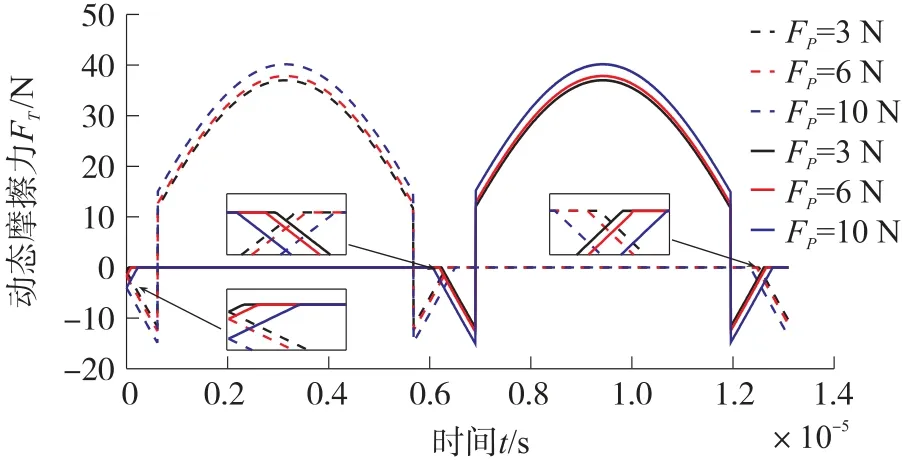
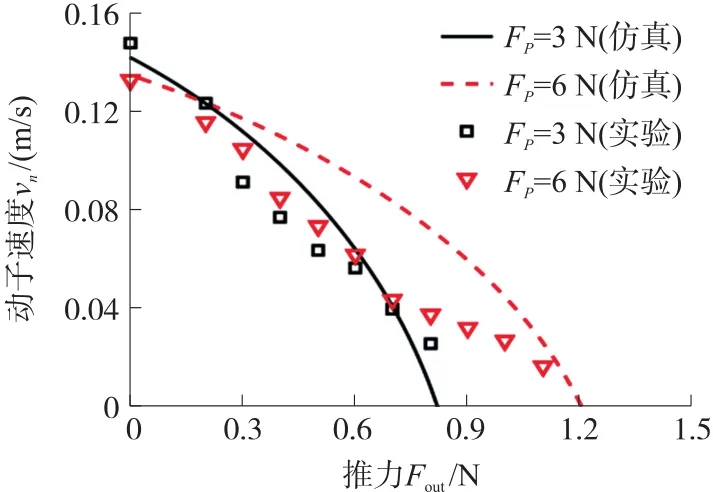
压电电机的摩擦传动依靠定/动子接触面摩擦力实现,即为定/动子接触面切向力。在定/动子稳态运行接触阶段,假设动子的速度一段时间内是恒定的。在动/定子的切向接触力作用下,定子的切向振动速度vτ(vτ=Uωsin(ωt))与动子的滑动速度vn可以分为三种情况讨论:①当vτ>vn时,接触面摩擦力对动子产生加速驱动作用;②若vτ 从上述分析可知,一个周期内接触面摩擦力对外做功有正负之分,其与定/动子接触时间和等速时间间隔的相对大小有关。如图3(a)所示,驱动足与定子接触过程中,当接触时间Δt大于等速时间间隔Δp,接触时刻t1、t2对应的区间包含两个等速时刻p1、p2,接触时间t1~p1和p2~t2段,vτ-vn<0,接触面摩擦力做负功;接触时间p1~p2段,vτ-vn>0,接触面摩擦力做正功。在图3(b)中,驱动足与定子接触过程中,当接触时间Δt小于等速时间间隔Δp,两个等速时刻p1、p2不在两个接触时刻t1、t2对应的区间内,整个接触时间段vτ-vn>0,接触面摩擦力做正功。从图3 中更清晰地看出,双驱动足在一个周期内实现两次驱动。结合库仑摩擦定律,接触面摩擦力表达为: 图3 定/动子之间的速度关系 式中:μs和μd分别为静摩擦系数和动摩擦系数。 一般摩擦问题动摩擦因数是恒定的,而对于压电电机的摩擦问题,由于超声减摩效应,动摩擦因数是一个变量,界面摩擦力会随着法向和切向的超声振动而减小,且法向振动影响更大[9,14]。相关实验已经证明界面摩擦系数与界面法向振幅呈指数方式递减[15],两者之间的表达式为: 式中:AN可等效为驱动足的法向振幅,为忽略法向振动影响的动摩擦因数,取0.3。aμ和bμ分别表示超声振动下摩擦系数衰减极限值和衰减率,考虑到超声减磨率较高,aμ取0.15,由于法向振幅一般为微米级,bμ取1×106[16]。 当压电电机稳态运行时,忽略摩擦驱动耗散能,稳态输出力可看成动态摩擦力在一个周期内的平均值,其表达式为: ①当vτ-vn<0,接触面摩擦力对动子起减速制动作用,其表达式为: ②当vτ-vn>0,接触面摩擦力对动子起加速驱动作用,其表达式写成: 本新型双足压电电机,其左右驱动足与动子,一个周期内各接触一次,其稳态输出力表达式为: 以设计的新式双驱动足压电电机为研究对象,探究界面参数对动子与定子接触面动态接触法向力、切向摩擦力以及稳态运动输出特性的影响。表1所示为双驱动足压电电机的参数设置。 表1 压电电机的主要参数 基于双足压电电机动态法向力接触模型式(3),分析不同界面等效刚度kf,法向振幅W,预压力Fp对其动态法向力的影响关系,如图4~图6 所示,其中左驱动足为虚线,右驱动足为实线。 图4 不同界面等效刚度下法向动态接触力变化 从图4 中可以看出,左右驱动足的法向动态接触力呈相似的周期性变化,当一个驱动足法向动态接触力为零时,另一个驱动足法向动态接触力大于零,可实现交替驱动,但在将要实现交替驱动的短时间里,存在两驱动足法向接触力同时大于零的情况。在其他参数不变的情况下,等效刚度大的接触面间,其法向接触力也大,从局部放大图中可以看出,等效刚度越小,两驱动足同时接触动子的时间就越长。 从图5 中可以看出,在其他参数确定时,随着法向振幅的增大,定/动子接触界面法向接触力也随之增大。而从局部放大图中看出,法向幅值越大,两驱动足同时接触动子的时间反而越短。 图5 不同法向振幅下法向动态接触力的变化 从图6 可以看出,随着预压力的增大,接触时间和法向动态接触力都会变大,两驱动足同时接触动子的时间也会随之增长。 图6 不同预压力下法向动态接触力变化 通过上述接触面动态法向力的分析可知,动态摩擦力也呈现周期性变化,且双足有相似的变化规律。根据式(5)和式(6),分析不同界面等效刚度kf、不同动子速度vn、预压力Fp对其动态法向力的影响关系,如图7~图9 所示,其中左驱动足为虚线,右驱动足为实线。 图7 不同界面等效刚度下动态摩擦力的变化 从图7 中可以看出,随着接触界面等效刚度的变化,动态摩擦力做效功的时间不变。等效刚度越大,定子与动子之间的等速点上升,输出的动态摩擦力幅值越大。同时,较大的等效刚度对应的负功也越大。 从图8 中可以看出,动子速度的变化,对定/动子动态摩擦力幅值的大小并无明显影响。但随着动子输出速度的增大,定子与动子之间的等速点上升,定子有效驱动动子的时间区域变窄,即动态摩擦力做正功的时间会减小,做负功的时间会增大。 图8 不同动子速度下动态摩擦力的变化 如图9 所示,随着预压力的增大,定子与动子之间的等速点上升,动态摩擦力的峰值增大,且接触时间也会增大,其中,定子起驱动作用的时间不变,起阻碍作用的时间增大,两驱动足同时接触动子的时间变长。 图9 不同预压力下动态摩擦力的变化 根据压电电机结构尺寸,加工制作样机,如图10 所示。其中,金属弹性体为硬铝2A12,压电陶瓷为PZT-8。 图10 压电电机定子样机 图11 机械性能实验测试平台系统 搭建压电电机实验样机测试平台,主要实验器仪器包含:FY2300H 系列双通道波形发生器、HFVA-42 型功率放大器、万用表、激光测速仪、阻抗分析仪(ZX70A- 500K,China) 等,如 图 11 所 示。FY2300H 双通道波形发生器产生两个同频且相位差为π/2 的正弦信号,经过HFVA-42 型功率放大器放大后,达到目标激励电压幅值,接入压电陶瓷上的引线,驱动电机定子。压电电机定子通过螺栓固定在滑块上,动子部分为直线型导轨,固定在底座的右挡板上,定子和动子的滑动方向为空间垂直,保证平稳驱动。预压力大小通过预压力弹簧的变形量来调整。压电电机的驱动负载可由动子的牵引砝码调节,引绳穿过负载悬吊滑轮,保持定位。滑块的速度由激光测速仪实时记录。 对该双足压电电机稳态输出特性进行研究,结合式(10)压电电机稳态输出力的数学模型,对动子速度和输出推力间的变化关系进行仿真和实验对比分析。仿真和实验过程中,激励电压幅值、激励频率和相位差分别为200 V、80.8 kHz 和π/2。在预压力为3 N、6 N 条件下,分别测试压电电机的输出推力与输出速度的关系,结果如图12 所示。从图12 中可以看出,压电电机的输出速度随着输出推力的增加而降低,适当增大预紧力可以提高压电电机的输出推力,最大推力约在1.1 N 左右。压电电机输出性能的仿真模型和实验测试相一致,但随着预压力的增大,误差会变大,这是由于预压力的增大使动定子的局部接触参数发生变化,整体刚度也会改变,而仿真过程参数是不变的,增加两者之间的差值。 图12 压电电机机械输出特性曲线 本文以新型双驱动足压电电机为研究对象,对其输出特性接触模型进行了研究,分析了电机定子振幅、预压力等参数对电机输出性能的影响。可以实现对电机机械特性进行预测和评估,并为电机后续的优化提供了方向。 研究定子与动子之间的接触摩擦机理,基于能量守恒定律,考虑超声振动对摩擦系数的影响,建立定子与动子之间的非线性接触方程,研究了接触刚度、预压力等电机参数在一个周期内对于电机的动态法向接触力、动态摩擦接触力的影响。搭建压电电机实验测试平台,研究了不同预压力下,在电机稳态状态下电机的输出性能,并与电机的数值仿真模型相对比,从而验证电机接触数学模型的正确性。 此外,从分析中可以看出,双足压电电机虽然一个周期内实现驱动足对动子的两次驱动,提高了压电电机的驱动效率。但是两驱动足存在驱动重叠现象,因此需要进一步优化电机驱动足位置,减少两驱动足相互做负功的影响,设计更高效的驱动控制,进一步改善双足压电电机的驱动性能。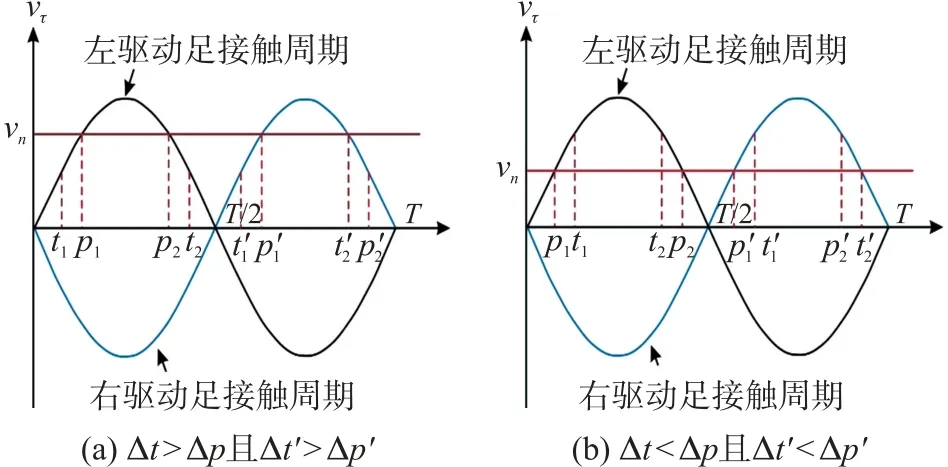
2.2 压电电机稳态输出力模型
3 案例分析

3.1 接触面的法向动态力

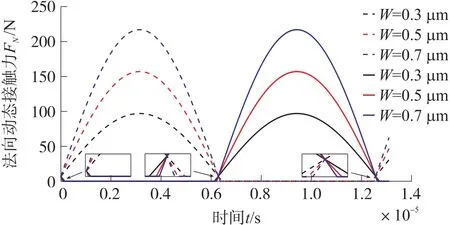

3.2 定/动子界面动态切向摩擦力
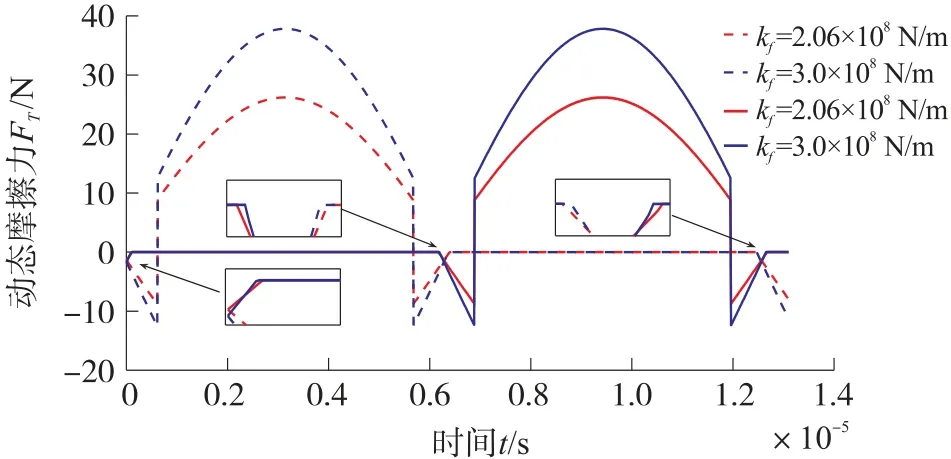

4 实验验证和分析
4.1 压电电机实验样机测试平台搭建


4.2 压电电机实验分析和验证
5 结论
