具有低纹波输出高增益DC－DC 变换器∗

王众毅，王德真，胡冠中

(1.许昌电气职业学院电气工程系，河南 许昌 461000；2.许昌学院电气与机械工程学院，河南 许昌 461000)

可再生能源，尤其光伏发电由于其清洁、无污染等优势而得到不断的关注和发展[1]。然而由于光伏电池产生的电压等级较小，因此需使用DC－DC变换器将其升压到所需的电压等级[2]。

目前常用的Boost 变换器因其成本低，结构简单而被广泛采用。但是该类传统升压电路电压增益低于5[3]。然而，硬开关会增加额外的传导损耗，降低效率。此外，二极管和开关管承受较高的电压应力。对此，文献[4]通过增加一相有源辅助电路以实现交错导通的运行模式。主开关由于断续模式(Discontinuous Conduction Mode，DCM)的运行模式，输出二极管的方向电压应力得到减少。然而，此类变换器需采用变频控制，这使用于减少电磁干扰的滤波电路设计变得困难。对此，学者提出了采用耦合电感的交错升压式变换器[5－6]。此类变换器拓扑输出二极管的反向电压较低。耦合电感的漏电感可实现半导体器件的零电流开关(Zero Current Switching，ZCS)。但是，该类变换器的耦合电感二次侧输出电流纹波较大，影响电能质量。对此，文献[7]提出三次交错Boost 变换器，并将电压应力降低一半。同时，与传统交错式Boost 变换器相比更适用于高增益场合。但是控制电路的设计较为复杂，难以量产。

近期，有学者提出将耦合电感和电压倍增单元相结合的新型拓扑[8－10]。此类变换器拓扑具有较高的电压增益和较低的开关管电压应力。此外，漏电感中存储的能量可以返回至主电路。鉴于此，文献[11－12]提出了一类基于二极管电容倍压器的交错式升压变换器。该类拓扑在无需变压器的情况下可实现高电压增益，且无需高的开关管占空比。但是缺点是主电路中二极管和开关管承受的电压应力较高，导致此类变换器设计成本较高，且损耗无法估计。

针对上述问题的不足，本文提出了一种新型的高增益DC－DC 变换器，在提升电压增益的同时减少了元器件的电压应力。文中分析了变换器的工作原理和性能特征，搭建了100 W 的实验样机对所提变换器的稳定性及可行性进行了测试。

1 本文所提变换器拓扑结构

图1 给出了本文所提一种新型高增益交错DC－DC 变换器的拓扑结构。该变换器可分为支路Ⅰ和支路Ⅱ两部分，在支路Ⅰ中，电感L1、MOS 管S1、二极管D3和电容C5构成的一个Boost 变换器，二极管D1和D2、电容C1和C2以及电感Lr1组成开关电容电路，从而提高变换器的电压。支路Ⅱ结构与支路Ⅰ类似。在所提变换器中，支路Ⅱ结构和支路Ⅰ结构对称，功率MOS 管S1和S2具有相同占空比，两者驱动脉冲相位相差180°，因此，可以有效降低输入电流纹波和输入滤波器的尺寸。与其他基于开关电容的高增益交错Boost 变换器不同，该变换器的占空比没有限制，对于大于或小于0.5 的所有占空比，变换器都能正常工作。

图1 所提变换器拓扑结构

2 工作原理

2.1 模态分析

所提变换器在CCM 模式下，每个开关周期内有6 种工作模态。图2 示出了所提变换器的关键工作波形。图3 给出了各工作模态的等效电路。为了简化分析，对所提变换器做出以下假设，所有元器件都是理想的；所有电容器都足够大，在一个开关周期内电容两端电压保持恒定。

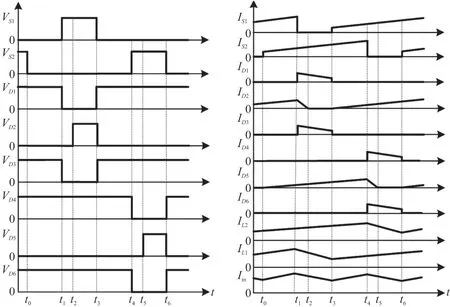
图2 所提变换器关键工作波形

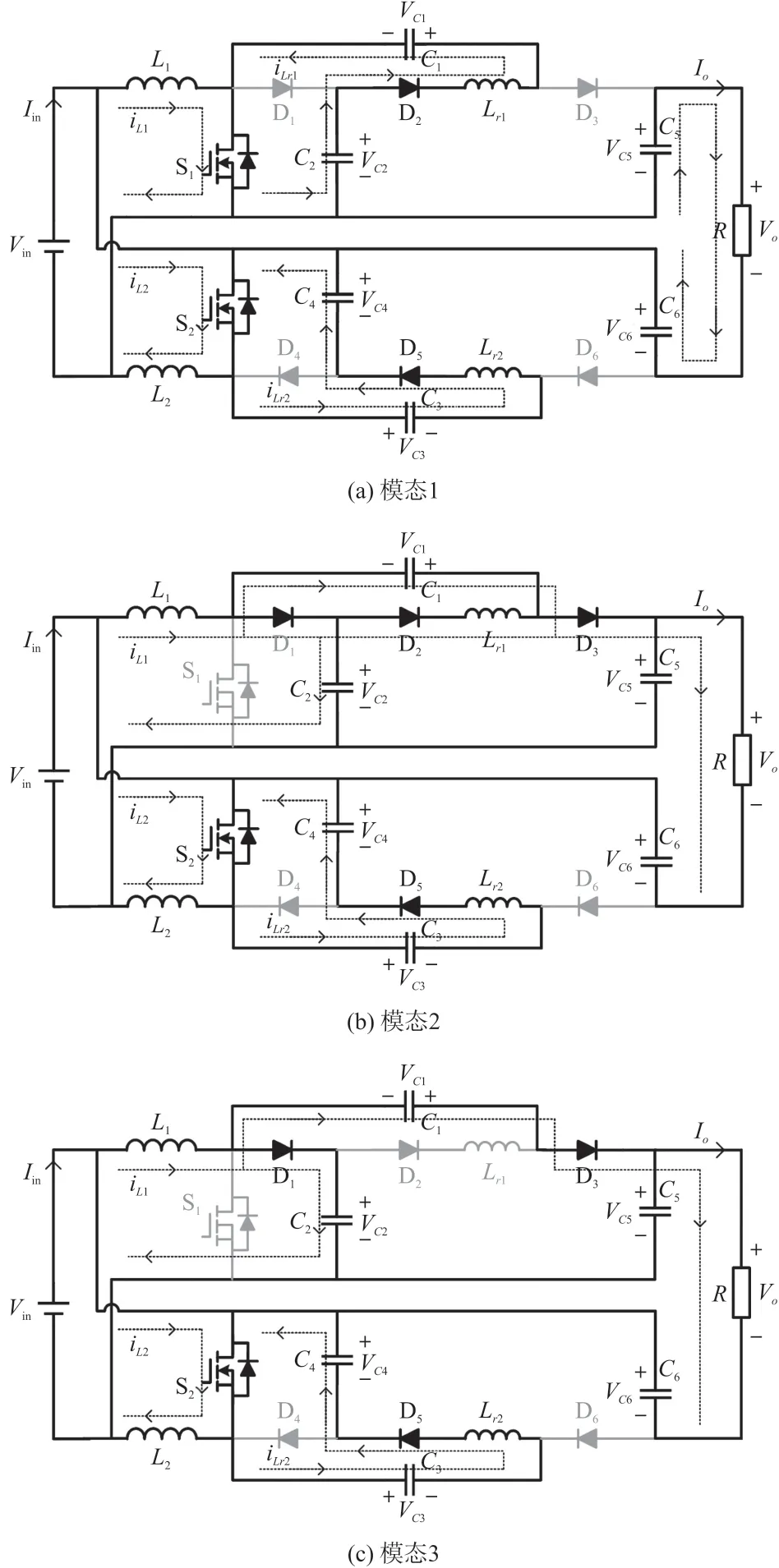
图3 所提变换器的工作模态

模态1:如图3(a)所示，变换器中的两个功率MOS 管S1、S2导通。电感L1和L2两端的电压等于输入电压，其电流线性增加。电容C2通过回路C2－D2－Lr1－C1－S1对电容C1充电，电容C4通过回路C4－S2－C3－Lr2－D5对电容C3充电，Lr1、Lr2的电流线性增加。负载电流路径为C6－Vin－C5－R。电感L1、L2、Lr1和Lr2的电流方程如下所示:

模态2:如图3(b)所示，功率MOS 管S1关断。支路Ⅰ中，二极管D1和D3导通，电感L1释放能量对电容C2和C5充电，电流线性减小。电感Lr1通过回路C1－Lr1－D2－D1续流，电感Lr1和二极管D2的电流线性减小至0，因此，二极管D2可以零电流关断。支路Ⅱ中各元件的运行状态同模态1，L2、Lr2的电流线性增加。在该模态下，电流方程如下:

模态3:如图3(c)所示，在此模态，支路Ⅰ中，二极管D2关断。电感L1中储存的能量一部分通过二极管D1对电容C2充电，另一部分通过二极管D3对输出电容充电，L1的电流线性减小。支路Ⅱ运行情况同上一模态。电流方程如下所示:

由于支路Ⅰ和支路Ⅱ交错运行，模态4 至模态6 的分析过程与模态1 至模态3 类似，此处不再赘述。

2.2 CCM 和DCM 之间的临界导通模式

若该变换器在临界导通模式下工作，则电感电流的最小值为零。电感L2的电流最小值为:

式中:D为占空比，iL2av、ΔiL2分别为电感L2的平均电流和纹波电流。因此，变换器在CCM 模式下运行时，电感最小值如下所示:

3 所提变换器的参数设计

3.1 功率器件设计

根据伏秒平衡原理，得到电容C1、C2、C3、C4、C5和C6的电压值如下:

在回路Vin－VC5－Vo－VC6中应用KVL 定律，可得:

将式(7)代入(8)中，并将其简化，得到所提DC－DC 变换器的电压增益为:

结合上一节的分析，每个功率MOS 管和二极管上的最大电压应力为:

3.2 储能元件设计

输入电感可根据以下公式计算:

式中:ΔIL为电感电流纹波，通常设计其为流过电感平均电流的40%。

变换器的输入功率为:

式中:Iainav为平均输入电流，结合式(9)可得:

每个输入电感中的平均电流相等，因此:

当开关S1在(1－D)Ts时刻关断时，流过电容C2的平均电流为Iainav/2。根据电容的电压负载方程，电容C2可计算为:

式中:ΔVC2为电容电压纹波。

类似地，电容C1、C3和C4的计算公式如下所示:

在每个开关周期内，输出电容C5和C6必须在DTs内为负载提供能量。由于输出电容串联，其容值可通过下式计算:

式中:ΔVo为输出电容电压纹波，大小为输出电压的1%。

当开关S1导通时，电感Lr1两端电压约为0.5×(ΔVC1＋ΔVC2)，假设电感电流线性增加ΔILr1，电感Lr1的值为:

电感Lr2的值同Lr1。根据上述公式，可以合理设计电感值来减小电感电流纹波，以防止MOS 管电压应力显著增加。此外，由于该电感上的电压较小，Lr1、Lr2的值通常为几微亨。因此，该电感不会显著增加电路体积。

4 比较分析

本节主要将所提变换器与传统Boost 电路以及文献[9]、[11]中的几种变换器拓扑进行了比较。图4 给出了各变换器的电压增益曲线比较。如图所示，在任一占空比下，与其他变换器相比，所提变换器的电压增益均高于其他类似变换器的电压增益。

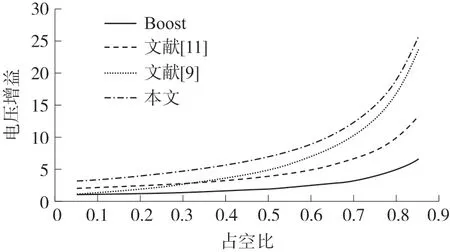
图4 各变换器输出电压增益曲线

表1 为各变换器结构与性能对比，由表1 可知，本文所提变换器电压增益较高，功率MOS 管和二极管电压应力较低，减小了系统损耗。

表1 变换器结构与性能对比

5 实验验证

为了验证所提变换器的正确性，搭建了一台功率为100 W 的实验样机。所选元器件型号和相关实验参数如表2 所示。

表2 实验电路参数

图5 给出了变换器的输入电压Vin、输出电压Vo、输出电流Io的波形图。稳态时所提变换器能够将30 V 的输入电压转换为300 V 输出电压，电压增益高，输出电流Io等于0.33 A。图6 给出了电感L1和L2以及输入电流Iin的波形，电感L1和L2在连续导通模式(CCM)下工作。Iin等于3.6 A，iL1和iL2均等于1.8 A，两者相位相差180°，此外，输入电流纹波远小于电感L1和L2的电流纹波，符合理论分析。

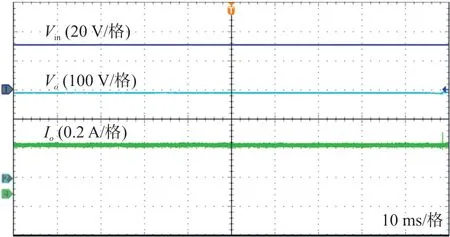
图5 Vin、Vo、Io 的波形图

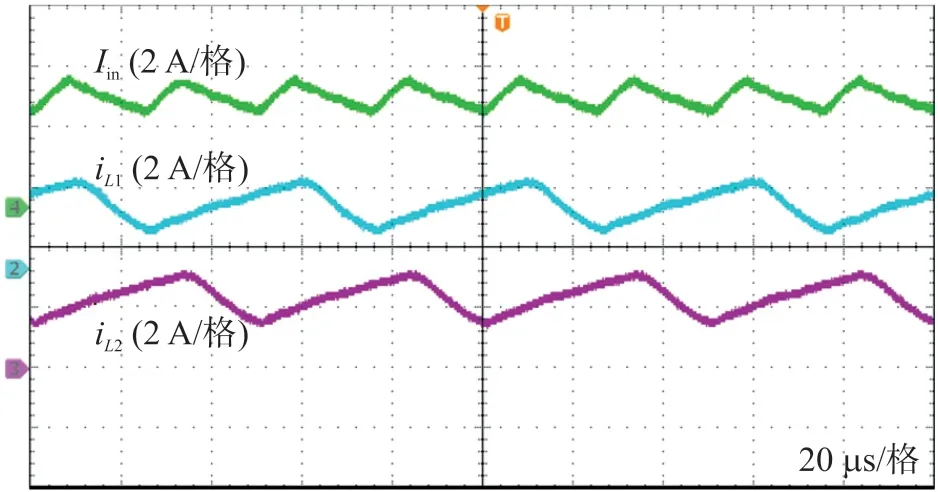
图6 iL1、iL2、Iin的波形图

图7 给出了功率MOS 管S1、S2的电流和电压波形，S2的电压波形与S1的电压波形相位相差180°，变换器的占空比约为64%。MOS 管的截止电压为87 V，远小于300 V 输出电压。此外，由图可知，当MOS 管关断时，不会产生尖峰电压。因此，可以使用低耐压的MOS 管来降低变换器的损耗。

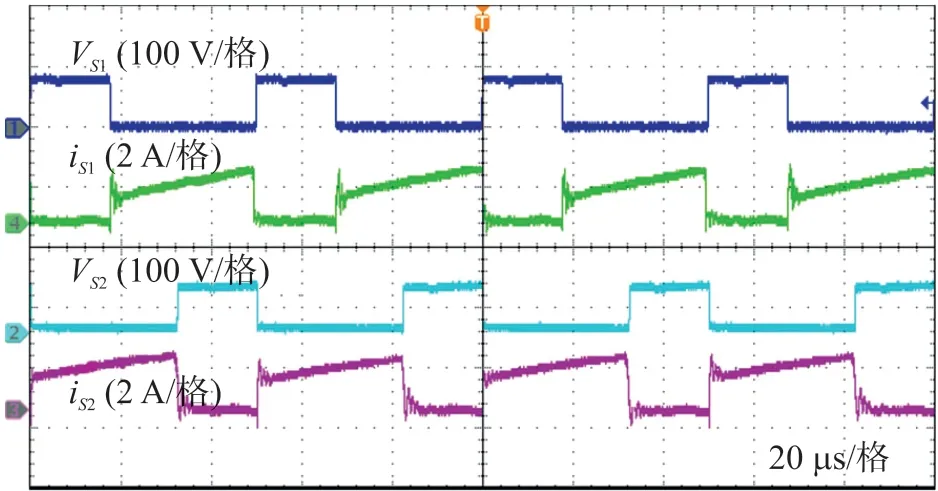
图7 S1 和S2 的电压、电流波形图

此外，图8 示出了所提变换器在不同输出功率下的效率曲线，由于MOS 管和二极管的电压应力低，并且变换器的二极管在零电流条件下关断，降低了传导损耗和开关损耗，实测最大效率高达92.7%。

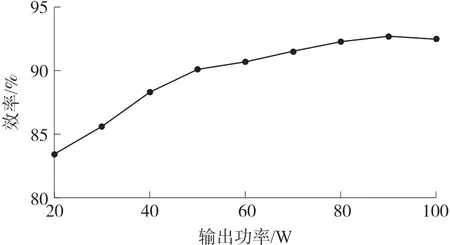
图8 所提变换器效率曲线

5 结论

本文提出了一种高增益DC－DC 变换器并对其工作原理进行详细分析，该变换器采用带开关电容的交错结构，可降低输入电流纹波。此外，由于二极管可实现零电流关断，降低了变换器损耗，可以获得更高的效率。对比分析了变换器在不同参数下的性能，所提变换器增益高，开关电压应力低。最后，对所提变换器进行的实验验证表明，其性能优异，并且设计简单、功率密度高，可广泛应用于需要高升压比的场合。