具有电压尖峰抑制能力的高增益Y 源逆变器∗

2024-01-29房绪鹏王煦超赵冰冰张胜男

电子器件 2023年6期

房绪鹏，王煦超，赵冰冰，张胜男

(山东科技大学电气与自动化工程学院，山东青岛 266590)

传统电压、电流源逆变器虽然已得到广泛应用，但仍存在许多缺点，如输出电压范围有限、发生开关管死区延迟或受到电磁干扰时易造成桥臂瞬时开路或短路等。阻抗源逆变器的出现很好地解决了上述问题。Z 源逆变器(Z-Source Inverter，ZSI)[1]允许同一桥臂开路或者短路，为按需升压或降压提供了一种机制，但其启动电流大、输入电流不连续的缺点限制了其应用和发展。准Z 源逆变器(Quasi Z-Source Inverter，q-ZSI)[2]、含有开关电感的Z 源逆变器[3－4]以及含有两绕组耦合电感的Trans-Z、Γ-Z 源逆变器[5－7]的出现改善了上述不足，并提升了电压增益。将三绕组耦合电感应用到电路中便形成了具有代表性的Y源逆变器(Y-Source Inverter，YSI)[8]及改进型Y 源逆变器(Improved Y-Source Inverter，I-YSI)[9]，I-YSI 结构如图1 所示，它拥有更加灵活的匝数比和更高的电压增益，因此获得广泛应用。然而，耦合电感的引入必然产生泄漏电感，当开关管动作时，逆变桥两端会产生很大电压尖峰，既对开关管的耐压和耐高温能力提出严苛要求，还会产生额外损耗。

图1 I-YSI 拓扑结构

为减少泄漏电感，可将耦合电感由Y 型改为△型[10]，但△型结构会使三绕组耦合电感形成独立回路，限制了匝数比选择的灵活性。另一种降低漏感影响的方法是增设缓冲电路，文献[11]将缓冲电路分为有源与无源两种，无源缓冲电路无需额外的控制与驱动部分，因此更加简便实用。文献[12]提出的无源缓冲电路仅需增设一个箝位二极管，但只能消除部分电压尖峰，且不具有泛用性。文献[13]中无源缓冲电路与原电路组成Buck-Boost 结构，可将直流链电压尖峰中能量回馈到主电路，但其元件参数要求严格，当电路发生波动时，现有的缓冲电路可能失去作用。文献[14]、文献[15]提出的缓冲电路适用于各类含耦合电感的阻抗源结构，既能有效抑制电压尖峰，还可提升电压增益，文献[16]提出仅由电容和二极管组成缓冲电路，是对前二者的简化，虽不能提升电压增益，但损耗更小，效率更高。

基于上述文献，本文提出一种具有母线电压尖峰抑制能力的高增益Y 源逆变器(Peak Suppression Improved Y-Source Inverter，SI-YSI)，既能有效减小元件应力，提升电压增益，还能够回收漏感能量，抑制直流链电压尖峰。

1 逆变器拓扑及母线电压尖峰分析

1.1 I-YSI 母线电压尖峰分析

I-YSI 拓扑结构如图1 所示，含有耦合电感漏感的I-YSI 等效电路如图2 所示，为方便分析，将逆变桥等效为单一开关SW，负载等效为电流源，SW 的导通时间与整个周期的比值定义为导通占空比d。当电路由直通状态进入非直通状态时，直流母线的电流突变，耦合电感各绕组中电流也随之迅速改变，进而导致漏感两端产生很大的电压差。

图2 I-YSI 等效电路

I-YSI 工作在直通状态时，各绕组中电流分别表示为:

工作在非直通状态时，各绕组中电流分别表示为:

式中:K＝(N1＋N2)/(N2－N3)，为耦合电感匝数比。

对比式(1)、式(2)发现，逆变器的开关管动作后，各绕组中电流变化很大，系统功率提高时，电流变化将进一步加大。根据漏感的伏安关系VLk＝LK(diLk/dt)，迅速变化的电流在漏感两端产生很大的感应电压，最终作用在直流母线上，产生电压尖峰。

1.2 SI-YSI 工作过程及母线电压尖峰抑制原理

SI-YSI 拓扑结构如图3 所示，左侧为新型Y 源结构，可有效减小元器件应力；右侧为附加缓冲电路，不但能回收泄漏能量，抑制直流链电压尖峰，还能进一步提升电压增益。

图3 SI-YSI 拓扑结构

含等效漏感的SI-YSI 在一个周期内的各工作状态如图4 所示，对应一个周期内[t0～t1]、[t1～t2]、[t2～t3]、[t3～t4]四个时段，各时段电路中简化关键波形如图5 所示。

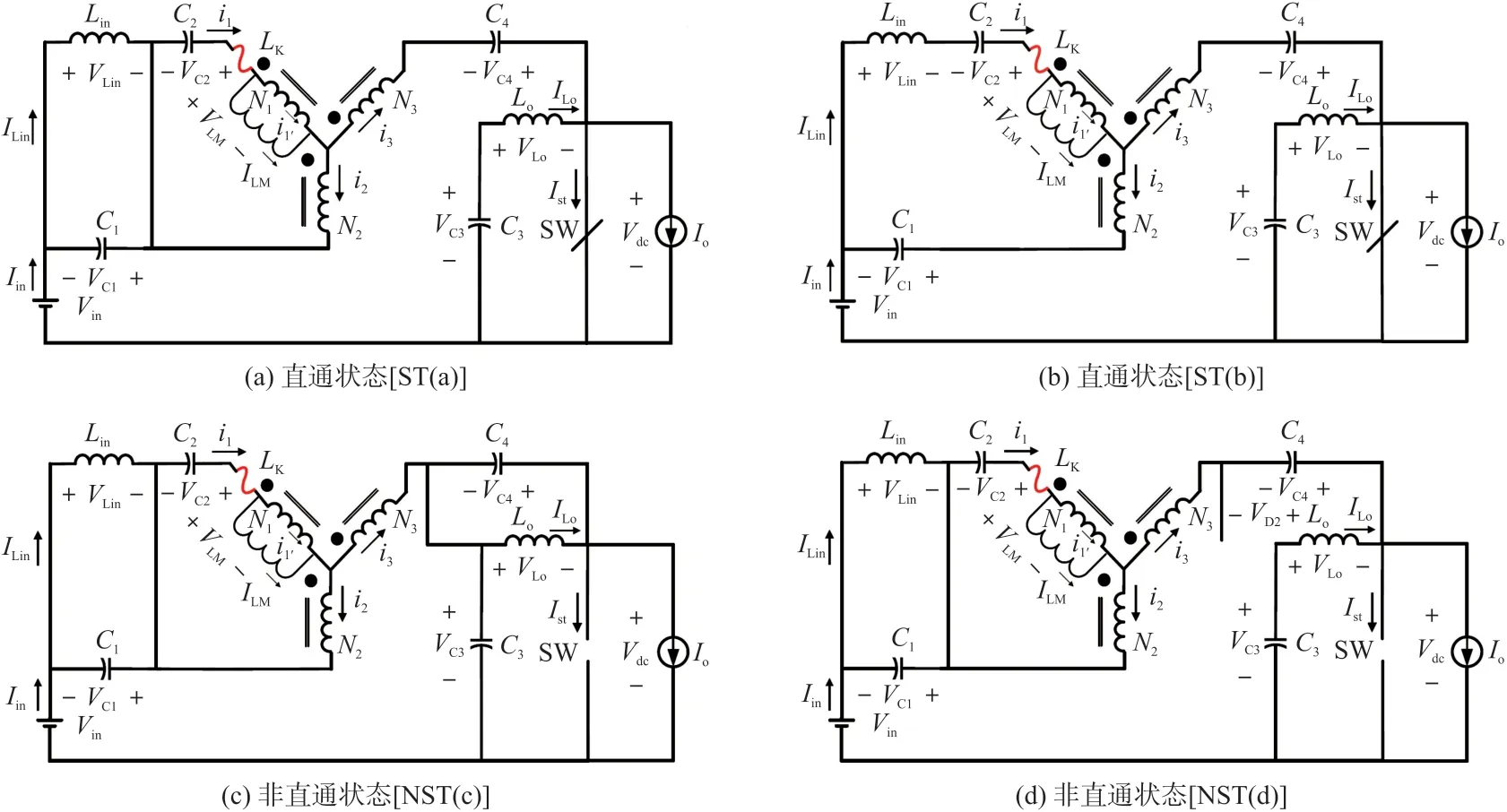
图4 SI-YSI 各工作状态图

图5 SI-YSI 简化关键波形图

图4(a)所示直通状态[ST(a)]:t0时刻，开关SW 因回路中电感的缓冲作用而发生零电流导通，二极管D1虽导通，但流过其电流迅速下降。二极管D2则承受反压保持关断。

图4(b)所示直通状态[ST(b)]:开关SW 保持导通，二极管D1中电流在t1时刻降至0 而关断，D2保持关断。输入电感Lin、输出电感Lo以及等效磁化电感LM在此期间线性充电，流过耦合电感的电流达到最大值，电容C1～C4在此期间线性放电。

图4(c)所示非直通状态[NST(c)]:开关SW在t2时刻关断，二极管D1、D2导通。从电流角度来看，逆变器直流母线电流此刻发生突变，但与I-YSI相比，变化的电流除了通过耦合电感，还通过二极管D2、电容C3进行分流，所以流经漏感电流变化缓慢，产生的感应电压较低。从电压角度来看，D2导通后，逆变桥、电容C3、C4形成了箝位回路，使直流母线电压尖峰得到很好的抑制。

图4(d)所示非直通状态[NST(d)]:二极管D1保持导通，D2关断。D1导通使互感线圈N1、N2、漏电感LK上的电压受到C2箝位保持不变。直流链电压此时等于电容C3、C4的电压以及二极管D2上一个很小的反电压。

与I-YSI 相比，SI-YSI 在每个周期内存在一个持续时间较长的NST(c)状态，此状态既给耦合电感中漏感电流变化提供了充足时间，又存在直流母线电压箝位回路，保证了直流母线电压尖峰的抑制。

2 稳态性能分析及对比

2.1 电流分析

由图5 不难发现，SI-YSI 各工作状态下的电流分度很大，由电流计算不但能够得到NST(c)状态在一个周期内的占比，还能得到各元器件的电流应力。

ST(a)状态持续时间极短，可省略此过程，从ST(b)状态开始，各电容电流表达式为:

NST(c)状态下，流过电容C1和C2的电流线性变化，流过电容C3和C4的电流因D2的导通而发生突变，表达式为:

NST(d)状态，流过电容C1～C4中电流均为恒定，表达式为:

由耦合线圈电流关系和基尔霍夫电流定律可得:

一个周期内对电容C1～C4电流使用安秒平衡原理，有:

求解上式得:

式中:a是NST(c)状态在一个周期内所占比例，定义其为非直通比例系数。Iin定义为输入电流在一个周期内的平均值。由式(8)可知，非直通比例系数a受K和d的影响，现实中往往要求d取较小值，此处设K为3，当d小于0.5 时，NST(c)状态在一个周期内的占比不低于0.25，此状态较高的时占比给耦合电感中漏感电流变化提供了充足时间。

另将式(9)、式(10)分别回代到ST(b)状态，可得到三绕组耦合电感的电流最大值，其表达式为:

2.2 电压分析

由基尔霍夫电压定律，选择合适的回路，可从ST(a)、ST(b)状态得出相同电压关系式:

NST(d)状态中，二极管D2虽保持关断，但其反电压近乎为0，所以将此状态与NST(c)合并计算，电压关系式为:

由互感线圈电压与匝数比关系可得:

一个周期内对输入、输出电感以及互感线圈N1使用伏秒平衡原理，有:

求解上式得各电容电压及输出直流链电压:

逆变器输出交流电压峰值与直流链电压关系为:

式中:B＝1/[1－(2＋K)d]，为升压因子，M为调制因数。

2.3 稳态性能对比

由上两节可得SI-YSI 主要元器件电压及电流应力表达式，将其总结在表1 中并与I-YSI 进行对比。二者的直流链电压增益对比如图6(a)所示，图中坐标为同一种变量的比值或无量纲常数，均无单位，可以看出，在直通占空比和耦合电感匝数比相同情况下，SI-YSI 具有更高的电压增益。

表1 两种逆变器稳态性能比较

图6 I-YSI、SI-YSI 稳态性能对比(K＝3)

为方便比较其他元件应力，规定两逆变器的输出直流链电压相同，即线圈匝数比需满足Kc＝K＋1，Kc为I-YSI 耦合电感线圈匝数比。由表中数据可知，SI-YSI 中互感线圈N1、N2的电流应力更小，而N3及逆变桥直通时电流应力则与I-YSI 中对应值相等。因此，无论是匝数比还是电流应力，SI-YSI 对互感线圈选型都提出了更少的要求。两逆变器电容C1、C2的电压应力对比如图6(b)、图6(c)所示，SIYSI 中两电容电压应力更小，额外增加的两个电容C3、C4的电压应力也较小。此外，SI-YSI 中二极管D1承受反压相对有所减小，其值仍较大，而新增二极管D2电压应力相对较小。

3 额外损耗分析

与I-YSI 相比，SI-YSI 中改进Y 源结构无新增元器件，但缓冲电路多使用了一个电感、一个二极管和两个电容，产生了额外的损耗，其中二极管、电感损耗较高，而电容的损耗较低，所以在计算中将其忽略。

3.1 二极管损耗分析

二极管D2的损耗主要有导通损耗和截止损耗，分别表示为:

式中:Vf为正向导通压降，IR为反向漏电流。由于二极管D2在NST(d)状态承受反压几乎为0，所以VD2仅为逆变器直通时二极管D2所承受反压。

3.2 电感损耗分析

电感的损耗主要由磁芯损耗和线圈铜耗组成。

磁芯损耗为:

式中:Ae为磁芯截面积，le为磁路长度，PL为磁芯损耗密度，可从磁芯损耗表或曲线中得出其计算式:

式中:a、b、c是由磁芯损耗曲线契合度决定的常数[17]，f为电感电流的频率，磁感应强度B由下述拟合公式给出:

式中:d、e、g、j、k、x为磁化曲线决定的常数[17]，磁场强度H与电感电流均值Iav、波动值ΔI及线圈匝数N有关:

电感的铜耗由电感电流有效值IL及线圈电阻RL产生:

最终，SI-YSI 的额外损耗表示为:

4 实验验证

基于理论分析，本文搭建了图7 所示I-YSI 及SI-YSI 实验样机，由TMS320F28335 型号DSP 产生控制信号，通过DA962D 驱动电路进行驱动，实验参数如表2 所示，实验波形如图8～图11 所示。

表2 实验参数

图7 I-YSI、SI-YSI 实验装置图

图8 I-YSI、SI-YSI 输出直流链电压

图8 为I-YSI、SI-YSI 输出直流链电压波形，可以看出，SI-YSI 输出直流链电压更高(理论值60 V)，而且当逆变器由直通转换到非直通状态时，I-YSI 因漏感作用产生了电压尖峰，SI-YSI 的电压尖峰得到明显抑制。

图9、图10 所示电流波形中，NST(c)与NST(d)两状态区分明显，NST(c)状态的周期占比约为0.44，与理论计算结果相符。其中各互感线圈电流在本工作状态下变化缓慢，不至使漏感两端感应出过高的尖峰电压，线圈电流峰值与表1 数据相符。

图9 输入电感电流波形及互感线圈电流波形

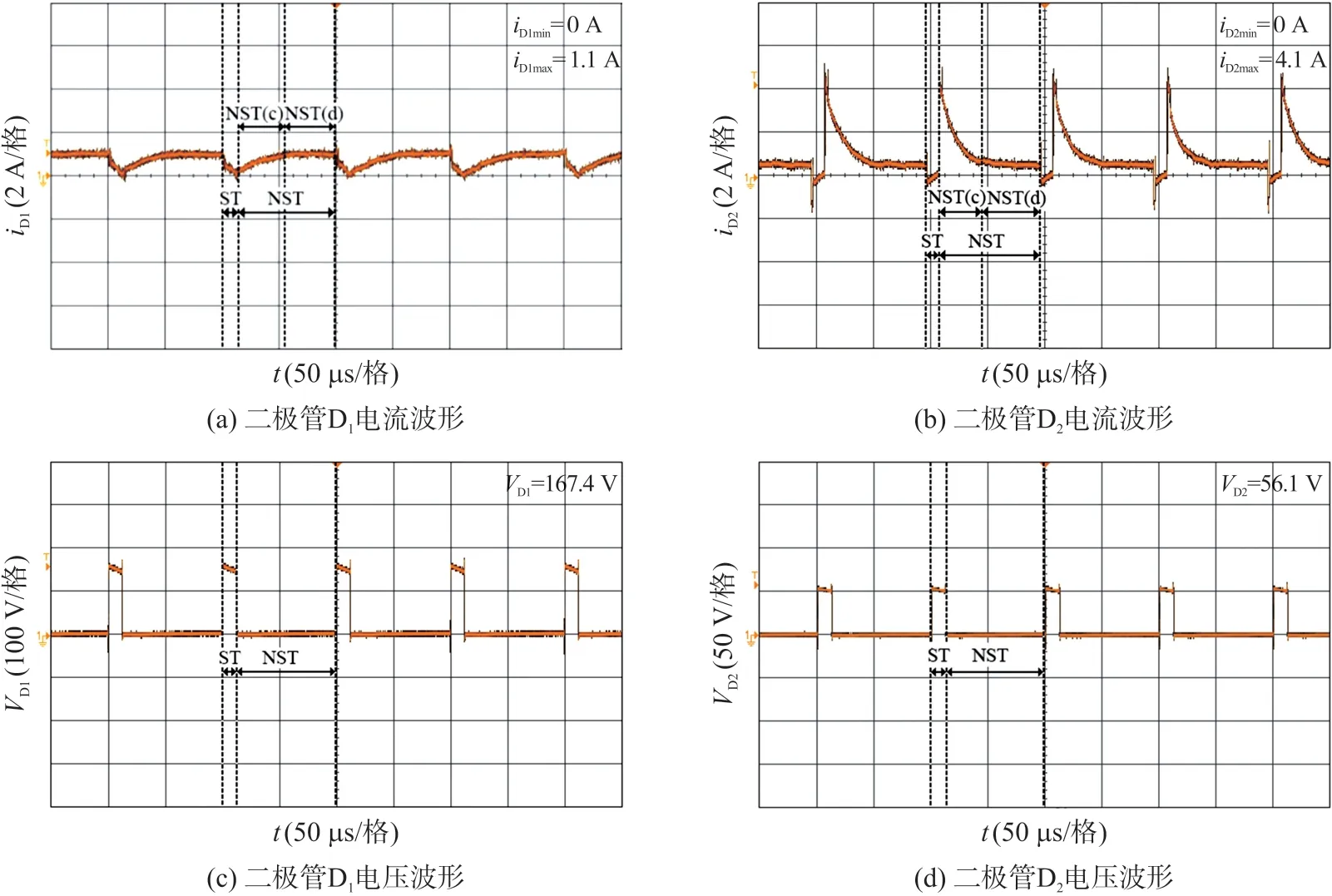
图10 二极管D1、D2 电流及电压波形

图10(c)、(d)分别为二极管D1、D2电压波形(理论值分别为180 V、60 V)，D2电压波形及直流链电压波形在整个非直通状态没有明显波动，验证了理论分析所述，NST(d)状态D2虽保持关断，但所承受反压几乎为0。

图11 为SI-YSI 输出交流电压波形(理论值为52.8 V)，其数值及上述各实验数值相对理论值均存在一定偏差，主要是受到泄漏电感、线路阻抗、器件压降影响，选择更加精密的元件以及采用PCB 制板将在一定程度上减小偏差。另外，如图12 所示，提高系统功率水平也将使各类损耗所占比重降低，进而提升系统效率。