巧算立方根之尾数魔法

吕佳夕

关于立方根的起源，可追溯到公元前429年，一场瘟疫袭击了希腊蒂洛斯岛。为了遏制瘟疫，国王要将阿波罗神殿中那个立方体的祭坛加大一倍（也就是要求做一个正方体，使它是已知正方体体积的2倍），这就是有名的“倍立方问题”。它和三等分角问题、化圆为方问题共称为尺规作图不能问题，也叫作古希腊三大几何问题。为了解决这个问题，[23]应运而生，这就是立方根的由来。

【故事原型】

我国数学家华罗庚在一次出国访问途中，看到飞机上邻座乘客的杂志上有一道智力题：求59319的立方根。华罗庚脱口说出答案，众人十分惊奇。华罗庚教授并没有使用计算机，也无法背出较大数的立方根，那他是怎么算出来的呢？

【分析探究】

华教授的计算方式是：

（1）确定位数。

103=1000，1003=1000000，而59319正好在1000和1000000之间，可以确定[593193]是一个两位数。

（2）确定个位上的数字。

59319个位上是9，也就是说，我们需要一个立方后个位上是9的数。1的立方个位上是1，2的立方个位上是8……9的立方个位上是9！所求两位数的个位上是9。是19，29，39，49……还是99呢？

（3）确定十位上的数字。

103=1000，203=8000，303=27000，403=64000，59319处于27000和64000之间，即303和403之间。那么所求数的十位上是3。

猜出答案：39。

進行验证，计算393，其结果刚好等于59319。

【真相揭秘】

其实，华教授计算立方根的方法就是我们今天要说的尾数魔法。我们已经知道，一个五位数或六位数的立方根，必是一个两位数。（确定数的位数）

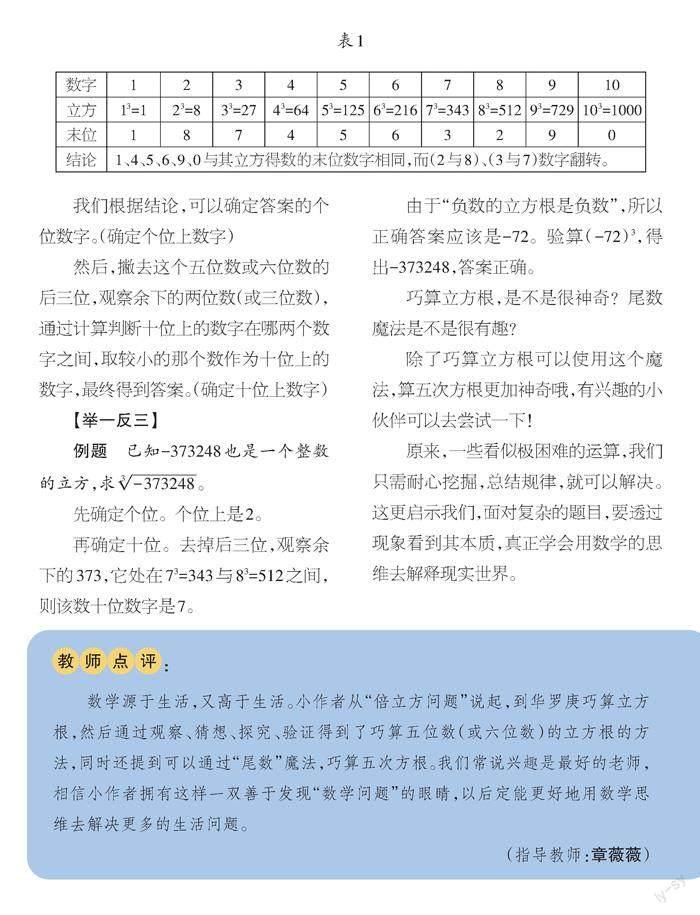
接着观察该数，由其个位数字推导出其立方根的个位数字，可参考表1：

我们根据结论，可以确定答案的个位数字。（确定个位上数字）

然后，撇去这个五位数或六位数的后三位，观察余下的两位数（或三位数），通过计算判断十位上的数字在哪两个数字之间，取较小的那个数作为十位上的数字，最终得到答案。（确定十位上数字）

【举一反三】

例题 已知-373248也是一个整数的立方，求[-3732483]。

先确定个位。个位上是2。

再确定十位。去掉后三位，观察余下的373，它处在73=343与83=512之间，则该数十位数字是7。

由于“负数的立方根是负数”，所以正确答案应该是-72。验算（-72）3，得出-373248，答案正确。

巧算立方根，是不是很神奇？尾数魔法是不是很有趣？

除了巧算立方根可以使用这个魔法，算五次方根更加神奇哦，有兴趣的小伙伴可以去尝试一下！

原来，一些看似极困难的运算，我们只需耐心挖掘，总结规律，就可以解决。这更启示我们，面对复杂的题目，要透过现象看到其本质，真正学会用数学的思维去解释现实世界。

数学源于生活，又高于生活。小作者从“倍立方问题”说起，到华罗庚巧算立方根，然后通过观察、猜想、探究、验证得到了巧算五位数（或六位数）的立方根的方法，同时还提到可以通过“尾数”魔法，巧算五次方根。我们常说兴趣是最好的老师，相信小作者拥有这样一双善于发现“数学问题”的眼睛，以后定能更好地用数学思维去解决更多的生活问题。

（指导教师：章薇薇）