空间引力波望远镜超前瞄准机构致动器电荷驱动位移行为研究

闫泽昊，周子夜，李 杨，周 虹，黄林海，顾乃庭*，饶长辉

1 中国科学院大学，北京 100049；

2 中国科学院光电技术研究所，四川 成都 610209；

3 中国科学院自适应光学重点实验室，四川 成都 610209

1 引言

LIGO (Laser interferometer gravitational-wave observatory) 于2015 年观测到两个黑洞合并时产生的引力波信号，直接证明了广义相对论对引力波的预言[1]，同时也打开了一扇天文观测的新窗口。相比于地基引力波观测台，空间引力波探测能够避开地表附近低频噪声、实现更长的臂长，从而能够探测1 Hz甚至更低频率的引力波[2]。目前，正在开展的空间引力波探测计划主要包括欧洲航空局的LISA[3]、我国“天琴计划”[4]以及“太极计划”[5]，他们均通过在空间搭建激光干涉仪探测自由运动验证质量块(proof mass)之间距离的变化，进而获得引力波信息[6]。空间引力波探测一般需要三组星载望远镜组成三角形星座，为了实现微弱引力波信号探测，三个星座间组成干涉仪的臂长一般长达数十甚至数百万公里，而距离的绝对测量精度需要达到皮米量级[7]。超远距离带来的不仅是距离测量困难，由于激光光束指向偏差会带来等效的相位误差，对于达到数万公里的干涉长度，要求实现nrad 级的超高精度指向控制，同时给三组星载望远镜之间的高精度跟瞄也带来了极大挑战。超前瞄准机构 (the point ahead angle mechanism，PAAM)[8]应运而生，其被放置于星载望远镜光学平台上，提供各组望远镜超前角度修正，校正“呼吸角”等引起的跟瞄误差。超前瞄准机构本质上是一种高精度激光光束指向机构，国内外不同空间引力波探测研究团队对其进行了深入研究：2009 年Henein[8]等基于两套压电陶瓷致动器为LISA 引力波探测任务设设计了一高冗余驱动、高稳定性的高精度指向校正机构，指向范围达到±1000 μrad、指向精度达到0.14 μrad；2010 年Rijnveld[9]等为 LISA 设计了另一种超前瞄准机构，设计了一种压电陶瓷致动器驱动、以Haberland 铰链为柔性支撑机构的高精度反射镜，指向范围达到±421 μrad、指向稳定性达到8 nrad/Hz1/2；2023 年朱伟舟[7]等人为我国空间引力波探测任务设计了一套超前瞄准机构，其采用柔性铰链与杠杆相结合的结构，并在压电陶瓷致动器的驱动下实现709 μrad 偏转范围、0.44 μrad 指向精度。在上述典型的PAAM 机构中，压电陶瓷致动器是其核心组成部分，其性能好坏直接决定了超前瞄准机构的偏转范围、指向精度、指向稳定性等各项关键性能。压电陶瓷致动器(piezoelectric actuators,PZA)一般由多个压电陶瓷晶圆堆叠而成，利用其逆压电效应在外部电压的激励下产生位移响应[10]，带动超前瞄准机构内部结构产生形变并最终使反射镜偏摆，实现对空间引力波探测望远镜的高精度指向跟瞄。相比于机电式致动器，压电陶瓷致动器具有分辨率高、频带宽、效率高、驱动力大、结构紧凑等优点，在高精度位移等领域得到广泛应用[11]。

然而，目前空间引力波探测PAAM 中的压电致动器均采用电压放大器作为激励信号源，压电陶瓷在电压驱动下的迟滞特性使压电致动器产生非线性响应[12]，这会引起PAAM 对激光光束指向控制过程中出现指向误差与指向抖动问题，从而大大降低PAAM 性能。在PAAM 中，一般在电压驱动的基础上采用高分辨力位移传感器做闭环控制[13]，但PAAM亚纳弧度的角位移对传感器性能要求极高，同时引入位移传感器会使系统过于复杂。为提升PAAM 性能，需对压电致动器位移响应行为建立准确的数学建模[14]，Bruno[15]针对干涉仪的开环控制提出一种基于Prandtl-Ishlinskii 迟滞算子的模型，在1.8 μm 的行程内，模型的最大误差不超过15 nm。高源蓬[16]建立的 Duhem非对称逆迟滞模型能有效描述压电执行器非对称逆迟滞曲线，模型输出与位移响应之间拟合相对误差为 0.79% (0.5 Hz)；Iyer[17]利用Preisach 模型对位移响应进行建模，使用自适应算法来有效地近似求解 Preisach 模型，对于1 Hz 正弦信号跟踪，在60 μm 的行程下存在±0.5 μm 的误差。但是，以上方法都是在电压驱动的基础上进行的，由于压电陶瓷位移响应的复杂性，还需要进一步深入研究。电荷驱动法从压电陶瓷位移响应与激励电荷成线性关系这一特性出发实现压电致动器的高线性度驱动，是一种值得尝试的方法，该方法最早由Main[18]提出，用于NASA NAOMI 项目中提升反射镜在数个致动器驱动下的响应线性度。如果能对电荷驱动下的位移响应行为做出定量分析，对于实现空间引力波探测望远镜超前瞄准机构的高精度指向控制具有重要意义。

基于以上背景，本论文提出基于等效电容计算方法来定量分析压电致动器在电荷驱动下的位移响应特性，并通过数值模拟仿真和实验验证等方式验证了计算方法的准确性和可行性。结果表明：在使用幅值5 V、频率0.05 Hz～5 Hz 正弦波信号控制的电荷放大器驱动某型号压电致动器时，采用本文方法分析结果与实验结果相比，二者位移响应最大偏差小于1.35%，为空间引力波探测望远镜超前瞄准机构的高精度指向控制提供了可能的分析方法和实现途径。本文第二节对空间引力波探测星载望远镜中超前瞄准机构基本原理进行详细阐述，并对致动器在电荷驱动与电压驱动下位移响应线性度等特性进行了深入对比分析；第三节深入分析了电荷驱动压电致动器的位移响应特性，并基于对压电致动器等效电容分析结果建立致动器位移响应模型；第四节阐述了实验验证方案，并给出了实验结果，验证方法正确性；论文第五节对全文进行了总结。

2 基于电荷驱动压电致动器的超前瞄准机构基本原理

2.1 星载引力波探测望远镜中超前瞄准机构工作原理

用于空间引力波探测的星载望远镜由激光干涉仪与望远镜两部分组成，其中激光干涉仪来探测两个自由悬浮的验证质量块之间距离的变化，望远镜的功能是将激光光束从一个航天器传送到另一个航天器[19]。如图1(a)所示，为了调节激光干涉仪发射光光束的角度，可变形的超前瞄准机构PAAM 被放置在激光干涉仪内部的激光发射路径的瞳孔平面[20-21]，PAAM 通过反射镜产生一个超高精度的偏摆角，使得远端望远镜能够准确接收到光束以完成星间激光干涉。尽管不同团队设计的PAAM 不同，但是所设计的结构都是为了实现压电致动器的位移形变 Δδ与 镜面倾斜角 α的线性转换[22]，图1(b)为压电陶瓷致动器驱动下的PAAM 基本工作原理，放大器对两个压电致动器施加大小相同、正负相反的激励信号，两个致动器产生位移± Δδ，镜面产生倾角 α，致动器位移与镜面倾角存在如下关系：

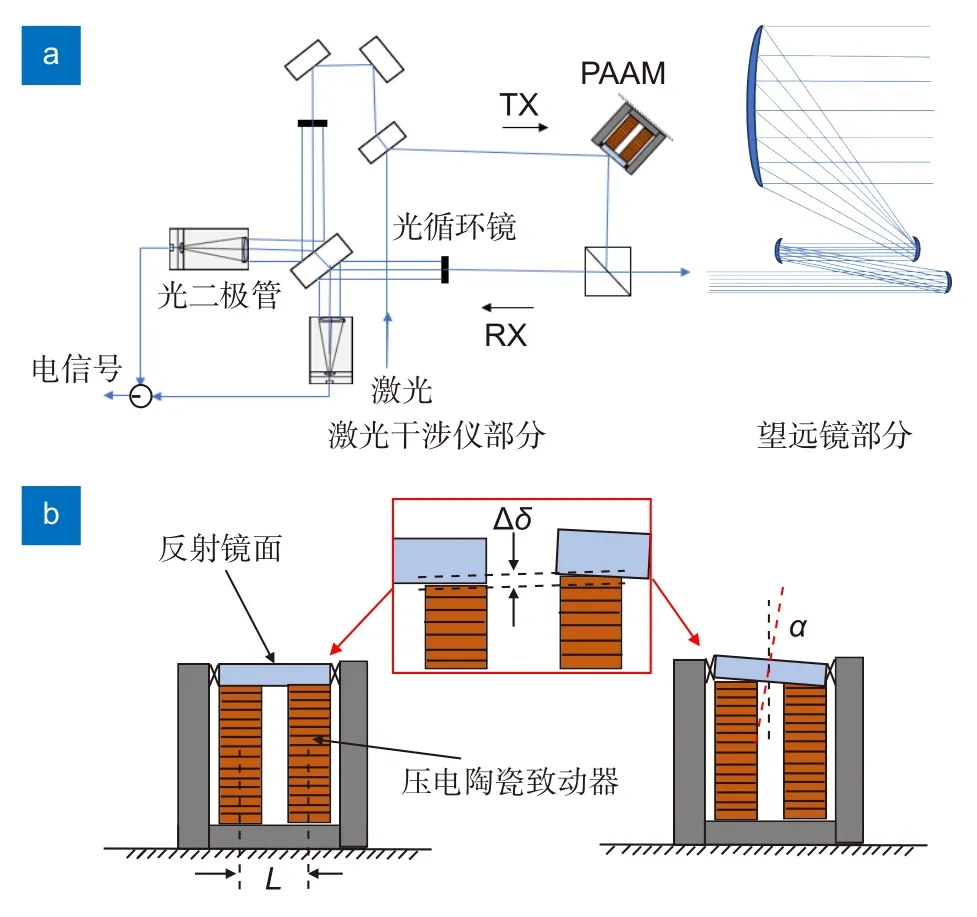
图1 星载望远镜中超前瞄准机构基本原理。(a) 星载望远镜基本原理；(b) 超前瞄准机构基本原理Fig.1 The principle of PAAM in spaceborne telescopes.(a) Basic principle of spaceborne telescope;(b) Basic principle of PAAM

式中：L是两压电致动器固定间距，因此镜面倾角α和位移响应± Δδ呈线性关系。目前空间引力波探测PAAM 中的压电致动器均采用电压放大器驱动，由于电压驱动下压电致动器存在迟滞效应，其迟滞效应所带来的位移响应 Δδ的 非线性将直接传递给指向角 α，压电致动器的位移响应非线性会严重影响引力波探测望远镜中PAAM 的指向精度。电荷驱动能有效避免压电致动器的迟滞特性带来的非线性响应，因此研究电荷驱动下压电致动器的位移响应行为，对于实现空间引力波探测望远镜超前瞄准机构的高精度指向控制具有重要意义。

2.2 压电致动器的电压驱动和电荷驱动方式

由于压电陶瓷致动器在电压电荷两种类型的放大器驱动下位移响应线性度不同，这里对两种放大器与压电致动器构成的驱动系统进行分析。由于压电陶瓷致动器本质上是由极板与电介质组成的器件，在对其进行电学分析时，普遍的做法是将其等效为一个电容Cp，但根据电介质物理，压电陶瓷的介电常数 ε0εr并不是一个定值，其等效电容Cp被称为非理想铁电电容(nonideal ferroelectric capacitors)[23]。图2 给出了两种驱动方式下驱动回路示意图，电压放大器的基本电路结构如图2(a)所示，在这种驱动方式下，运放直接对控制信号Vin进行线性放大，得到成比例放大的电压信号Vo。假设致动器的位移与电荷量存在恒定比例系数K，显然非理想电容Cp的存在使放大器始终无法通过Vin输 出成比例电荷量Qp，压电致动器也就无法产生与Vin成线性关系的位移响应。放大器输入信号Vin与位移响应L的关系如式(2)所示：

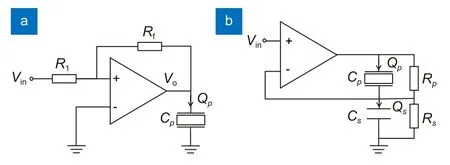
图2 压电陶瓷致动器的(a)电压驱动方式和(b)电荷驱动方式基本电路结构Fig.2 Basic circuit structures of (a) voltage driving mode and (b)charge driving mode of PZA

电荷放大器的基本电路结构如图2(b)所示。对电路分析得出压电致动器位移响应L与输入信号Vin间的函数关系，为了方便后续计算，这里写成s域表达式，如式(3)所示：

不难发现，当电路满足RpCp=RsCs时输入信号Vin与位移响应L呈线性关系，但非理想电容Cp的存在使等式无法成立，变化的Cp使压电致动器的位移响应L在信号频率较低(s趋于0)时仍无法保持与输入信号Vin的线性关系。但相较于任何信号下都无法保持线性响应的电压驱动方式，电荷驱动方式仍具有明显优势。

2.3 电压驱动与电荷驱动位移响应对比分析

为了验证压电陶瓷致动器在两种放大器驱动下产生位移响应的差异，这里对同一压电致动器分别用两种类型放大器驱动，实验使用激光测距仪对致动器位移数据进行采集，用采样电阻对放大器输出电流精确采集，以此计算放大器输出电荷量。这里对两种放大器分别输入5 Hz、1 Hz、0.5 Hz 正弦信号，对比此时输入信号与压电致动器位移响应间的关系。图3 为电压驱动下的位移响应及线性度，图4 为电荷驱动下压电致动器的位移响应及线性度。

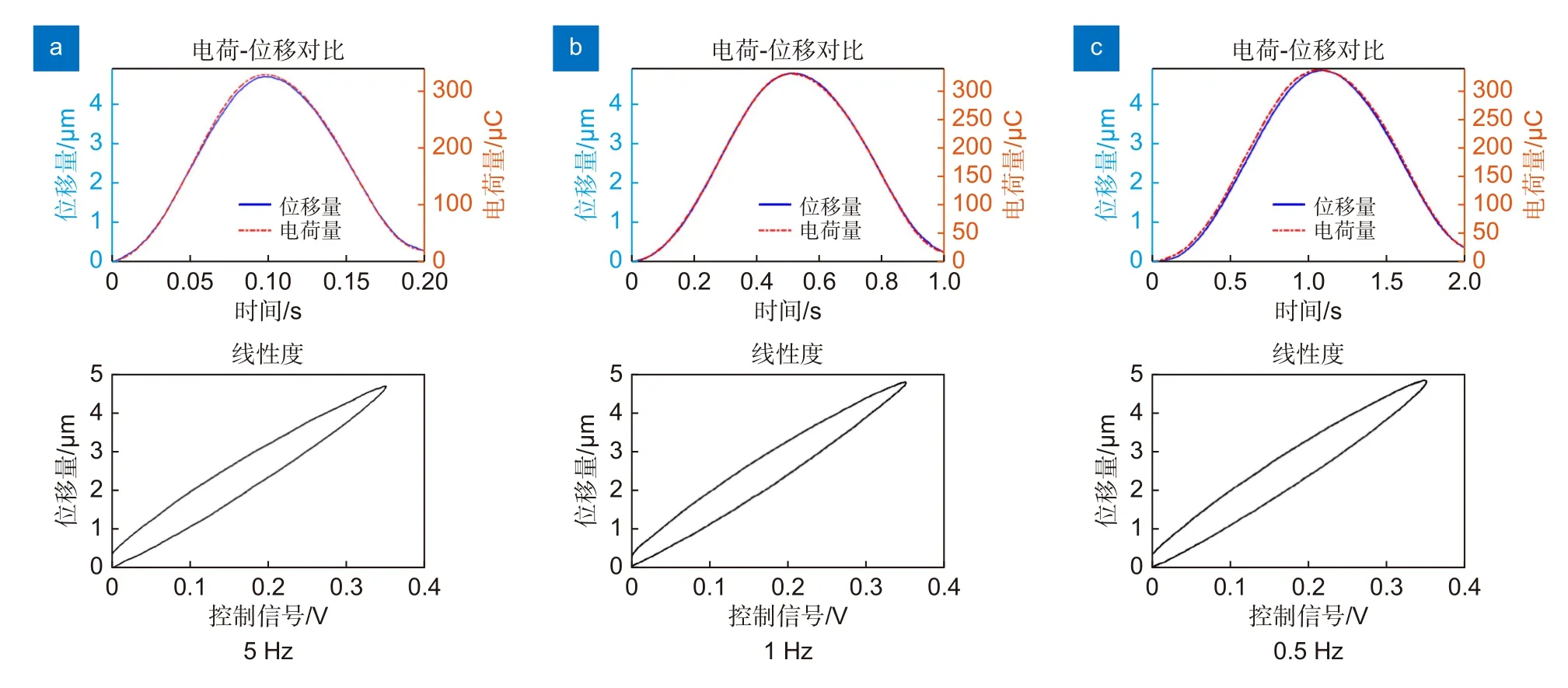
图3 电压驱动下压电致动器位移响应及线性度Fig.3 Displacement response and linearity of PZA under voltage drive

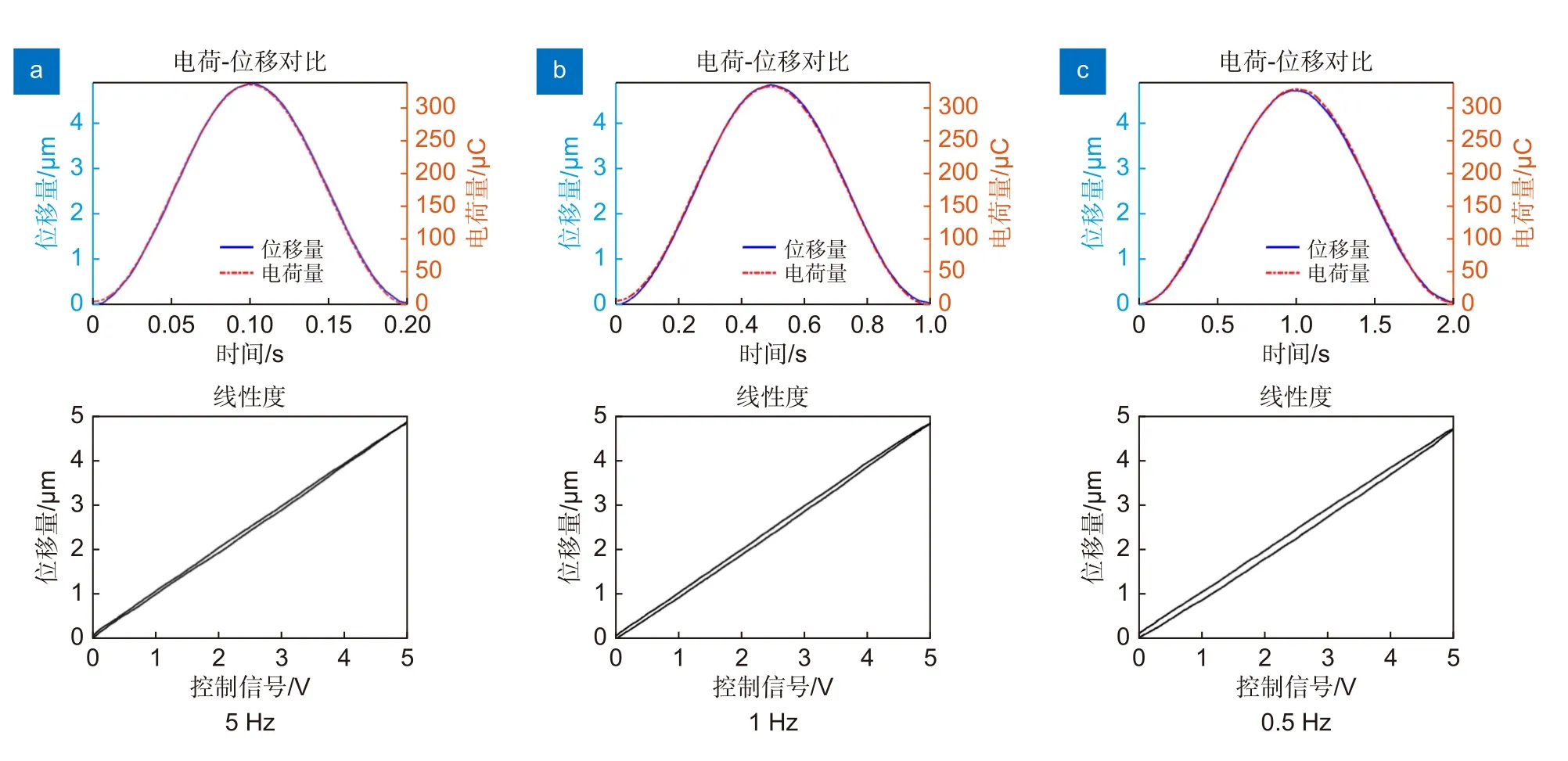
图4 电荷驱动下压电致动器位移响应及线性度Fig.4 Displacement response and linearity of PZA under charge drive

结果显示，压电陶瓷致动器在5 Hz、1 Hz、0.5 Hz 频率的电压激励信号驱动下位移响应线性度始终较差，其线性度分别为13.27%、12.53%、12.66%，在同样频率的电荷激励信号驱动下的位移线性度分别为1.75%、1.80%、2.55%，在信号频率较低时出现线性度变差的趋势。此外，在整个过程中两种放大器输出电荷量始终与PZA 位移成正比例关系，二者存在恒定比例系数K=0.014 m/C，这也证明了电荷与位移间的线性关系。总之，基于电荷驱动的压电致动器的位移响线性度要优于电压驱动。

3 电荷驱动压电致动器位移响应行为研究

3.1 压电致动器等效电容变化特性分析

根据式(3)对电荷驱动回路的描述，为了准确得出电荷驱动下压电致动器的位移响应，需首先得知其等效电容Cp在激励信号下的变化情况。根据电容的动态特性，压电致动器等效电容的容值可用电荷的变化率与电压的变化率之比来计算，这就需要获得压电致动器在激励信号下的电压变化曲线与电荷变化曲线。对于压电致动器组成的非线性电容，其电压与电荷间存在复杂的映射关系，这给不同信号下电压变化曲线与电荷变化曲线的获取及后续电容的计算带来困难。但二者的映射关系仍有规律可循：根据上文介绍，压电致动器的位移与其电荷量具有直接线性关系，因此可以用压电致动器在不同信号下所表现出的电压-位移迟滞特性直接推导出对应的电压-电荷映射关系，从而便能方便得出对应信号下电压变化曲线与电荷变化曲线及等效电容的变化曲线Cp(t)。

对于压电致动器的迟滞非线性特性，目前已经有大量研究做出分析，这里对激励信号的幅值、频率、波形对致动器电压-位移迟滞特性的影响展开介绍。对于不同幅值的激励信号，压电致动器迟滞曲线会随激励信号幅值改变，这意味着其电荷-电压映射关系也会随着信号幅值改变。图5(a)给出了不同幅值的正弦波电压激励信号下的电荷-电压映射关系，显然其等效电容在不同幅值的信号下的变化情况是不同的。对于不同频率的激励信号，压电致动器的迟滞曲线在频率较低的一定频段范围内相同，即表现出频率无关性。这意味着低频时在同样波形信号的驱动下，压电致动器的电荷-电压映射关系不会随频率发生改变，如图5(b)所示。此外，对于不同波形的激励信号，在相同的输入信号极值范围内压电致动器的迟滞曲线是一致全等的，迟滞曲线与信号的具体波形无关，即一致性。图5(c)给出了电压驱动、电荷驱动下的相同幅值范围的三角波、正弦波激励信号时的电荷-电压映射关系。

图5 压电致动器的Q-U 映射关系与激励信号的关系。(a) 信号幅值；(b) 信号频率；(c) 信号波形Fig.5 The relationship between Q-U mapping and excitation signal of PZA.(a) Signal amplitude;(b) Signal frequency;(c) Signal waveform

经过以上对压电致动器电压-电荷映射关系的分析不难得出，尽管其映射关系在不同激励信号下复杂多变，但电压-电荷映射关系在某些情况下是相同的：低频信号下同样振幅信号的频率、波形变化不会引起映射关系再次变化。因此，在实际使用时，在测得某激励信号下压电致动器电压变化曲线与电荷变化曲线，并计算出二者映射关系与电容变化曲线Cp(t)后，能够得到与该激励信号相同极值范围、不同频率的激励信号下的映射关系与电容变化曲线。

以正弦电荷激励信号为例，当给予压电致动器5 Hz 的信号时，测得此时压电致动器电压变化曲线与电荷变化曲线，可得出二者映射关系与电容变化曲线Cp(t)，如图6 所示。根据上述推论，在对5 Hz 信号下的等效电容进行拟合后，能够直接推导出2 Hz、1 Hz 等频率的同样幅值的正弦激励信号下的等效电容的拟合公式。而不再需要对这些信号过程中的电压电荷变化进行实时测量，这大大简化了等效电容的计算，对于推断不同信号下的等效电容变化具有重要意义。

图6 压电致动器在正弦信号激励下的(a)电压-电荷映射关系及(b)等效电容变化情况Fig.6 (a) Voltage-charge mapping relationship and (b) equivalent capacitance variation of PZA under sinusoidal excitation

3.2 电荷驱动的压电致动器位移响应数学模型

式(3)给出了电荷驱动下压电致动器的位移量L与输入信号Vin间的传递函数，将其写为时域表达式，如式(4)所示：

假设等效电容在某信号Vin(t)下的变化情况用多项式Cp(t)=at2+bt+c拟 合，将Cp的拟合函数代入式(4)，得到系统输入信号Vin与压电致动器位移响应L间的一阶微分方程数学模型，如式(5)所示：

图2(b)中Qp是电荷放大器真正传递给压电致动器的电荷量，是致动器存在失真现象的真实位移响应的体现，而Qs是在输入信号控制下期望通过反馈电容Cs传递给压电致动器的电荷量，是致动器无失真理想位移响应的体现，式(6)给出了系统输入信号Vin与压电致动器理想位移L′间的数学模型：

因此，在得知输入信号Vin(t)及其等效电容变化曲线的拟合函数Cp(t)后，将其代入位移响应模型式(5)与式(6)中，可解出对应真实位移与理想位移响应。对某压电致动器在1 Hz 正弦信号激励下得出的真实位移与理想位移响应情况及二者线性度如图7 所示。

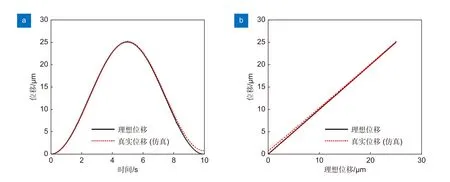
图7 (a) 压电致动器的真实位移与理想位移响应及(b)二者线性度Fig.7 (a) Real displacement and theoretical displacement response of PZA and (b) the linearity of both

4 实验验证

4.1 实验系统

为了验证以上关于压电致动器等效电容变化理论推导的正确性，本节对电荷驱动下压电致动器的位移响应开展实验，并与推导得出的位移响应做对比。为此搭建图8 所示实验平台，平台可对放大器的输入信号、压电致动器位移响应，以及放大器输出电流精确采集，实验平台工作流程如下：位于上位机的信号发生平台将控制信号经数据采集卡1 发送给放大器，控制信号经放大器放大后产生激励信号给压电致动器，再利用位移传感器测得压电致动器实时位移量，同时串联电流采集电阻对放大器输出电流进行超高速率采集，对电流数据在时间上积分得到对应时间的电荷量。信号发生器的控制信号、电流采集电阻采集信号、位移传感器的位移信号均由数据采集卡2 接收并将数据、波形存储、显示于上位机。

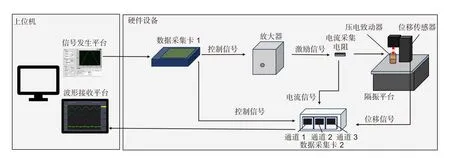
图8 压电致动器位移响应实验平台框图Fig.8 PZA displacement response experiment platform block diagram

实验平台实物图如图9 所示，平台使用电压放大器为PI E-508.00 放大器；电荷放大器为PI E-506.10模块化电荷放大器，二者输出电压均可达100 V 以上，值得注意的是：E506.10 内部的Rp=10Rs，一般每次在驱动不同的PZA 时都要替换与之小信号电容值成10 倍关系的反馈电容Cs；压电致动器为PI P-840.6，可在0～100 V 的输入电压范围内输出90 μm 最大行程；位移传感器采用KEYENCE LK-H025&LK-HD500 激光式位移传感器，精度可达0.001 μm；隔振平台采用Minus K BM-8 被动隔振平台，相较于传统气垫隔振性能提升10～100 倍；采集卡1 采用ART USB-2872A-D，采集卡2 采用KEYENCE NR-X100 采集模块，二者最大采样率均可达到1 MHz；电流采集电阻采用精度 1 Ω±0.01%、温漂±5 PPM 的金属箔电阻RJ711。

图9 压电致动器位移响应实验平台实物图Fig.9 Physical diagram of PZA displacement response experiment platform

4.2 实验结果及分析

在上述实验平台中，用电荷放大器E506.10 对静态电容10 μF 的P-840.6 压电致动器进行驱动。对电荷放大器分别输入峰值为5 V，频率为5 Hz、2 Hz、1 Hz、0.5 Hz、0.2 Hz、0.1 Hz、0.05 Hz 的正弦波控制信号，以此得出真实位移响应。同时，根据上文提供的电容变化规律，在测得5 Hz 的Q-U 映射关系及电容变化曲线Cp(t)后，以此为标准可直接推导出其它频率的电容变化曲线，并将其代入位移响应模型得出仿真位移响应，之后根据各频率信号所对应位移响应不难计算出实测与仿真线性度的具体值以及二者误差。图10 给出了对这些信号作用下压电致动器位移响应的实测位移与仿真位移，结果表明，随着信号频率的降低，压电致动器理想位移与真实位移间的失真程度逐渐增大、位移响应线性度逐渐变差，此时信号Vin与位移响应L的线性关系越差，这与上文式(3)的表述相一致。图11 给出了实测与仿真的线性度的对比，结果表明，仿真结果与实际测试结果能够较好地拟合，二者最大偏差小于1.35%。受实验系统中设备性能限制，如非接触式位移传感器长时间使用时产生的位移漂移误差、电流采集后附带的噪声给电荷计算带来的累计误差等，这些在实验中存在的误差使实验结果与仿真结果无法完美拟合，同时也为更低频率下的仿真与实验带来了一定的困难。此外，尽管本文仅给出了针对某具体型号的压电致动器在特定正弦激励信号下的仿真与实验结果，但得益于本文提出的位移响应数学模型可灵活调节参数，该方法对电荷驱动的不同型号压电致动器以及不同幅值、频率的激励信号下具有通用性。

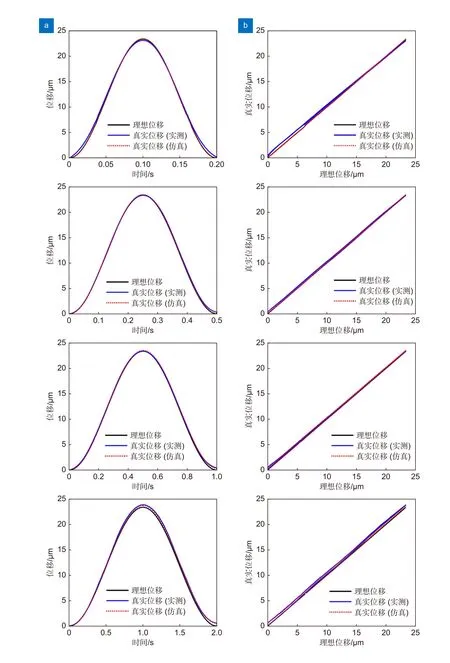
图10 电荷驱动的压电致动器位移响应线性度仿真与实测对比Fig.10 Comparison between simulation and measurement of linearity of displacement response of charge-driven PZA

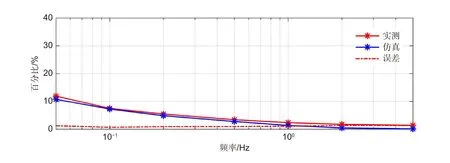
图11 不同信号下电荷驱动的压电致动器位移响应线性度仿真与实测对比Fig.11 Comparison between simulation and measurement of displacement response linearity of charge-driven PZA under different signals

5 总结与讨论

本文提出一种等效电容量计算方法来定量分析压电致动器在电荷驱动下的位移响应特性，并通过数值模拟仿真和实验验证两种方式验证了计算方法的准确性和可行性。结果表明：在使用5 V、0.05 Hz～5 Hz频率正弦波信号控制的电荷放大器驱动某型号压电致动器时，采用本文方法分析结果与实验结果相比二者位移响应最大偏差小于1.35%。受限于目前实验设备性能的限制，本文研究的信号频段范围相较于空间引力波探测领域的1 mHz～1 Hz 还有一定差距，后续通过采用更高性能的实验设备或重新设计电荷驱动电路等方法继续探索电荷驱动下压电致动器在更低频率下的响应情况，为空间引力波探测望远镜超前瞄准机构的高精度指向控制提供可能的分析方法和实现途径。