整体思想在三角函数中的应用

■吴 艳

三角函数中的公式较多,应用比较灵活,不少同学由于公式使用不当,常常陷入复杂的运算中。在解答某些三角函数问题时,若能仔细观察题目,注意与已知条件的联系,实现等价转化,采用整体思想进行求解,往往能起到很好的效果。

应用1:整体思想在姊妹关系sinx±cosx,sinxcosx 中的应用

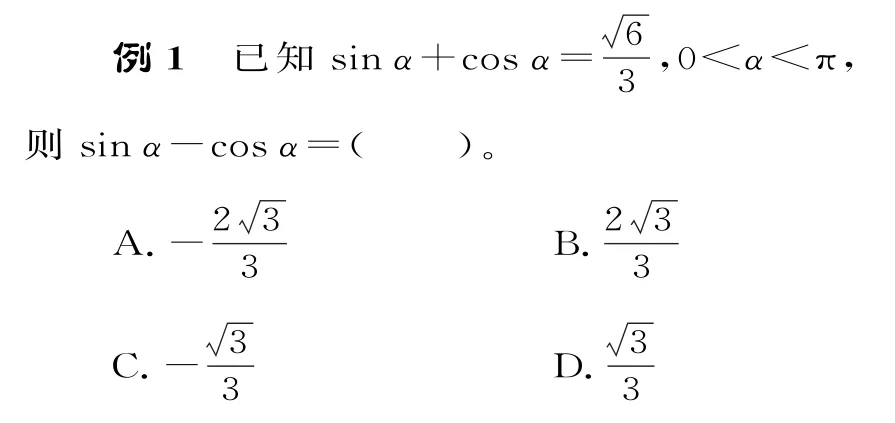
解:由(cosα+sinα)2+(cosα-sinα)2=2,直接使用整体思想求解。

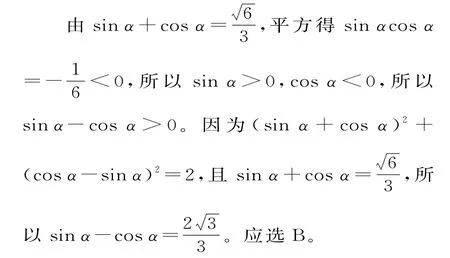
提 升:已 知sinx±cosx的 值,求sinxcosx或cos2x的值时,可利用(cosα+sinα)2+(cosα-sinα)2=2,结合cos2α=(cosα+sinα)(cosα-sinα)求解,凸显整体思想在姊妹关系sinx±cosx,sinxcosx中的应用。

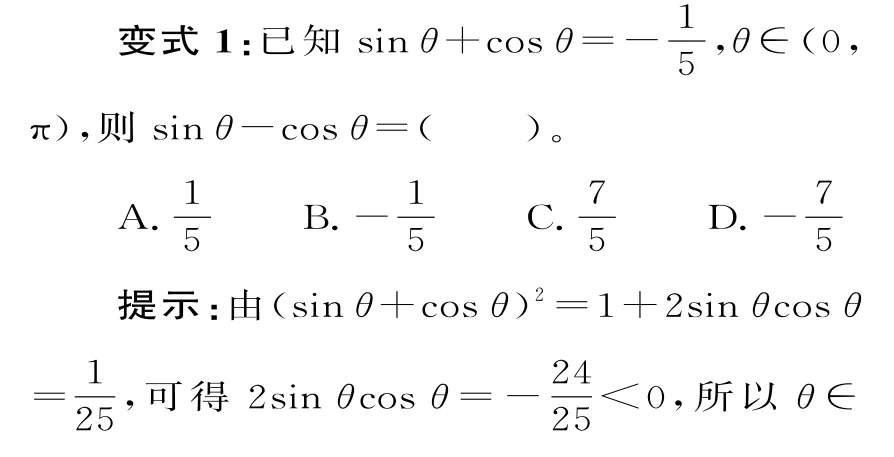
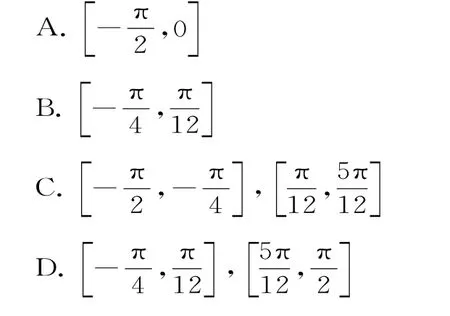
应用2:整体思想在三角函数性质中的应用

提升:解答这类问题,可通过诱导公式或三角恒等变换,将其转化为y=Asin(ωx+φ)+b或y=Acos(ωx+φ)+b的形式,结合正余弦函数的图像与性质求解。

应用3:整体思想在三角函数的最值或值域中的应用

例3 函数y=-sin2x+4cosx-6 的值域是( )。

A.[2,10] B.[0,10]

C.[- 2,10] D.[-10,-2]

解:由sin2x+cos2x=1,可得y=-sin2x+4cosx-6=cos2x+4cosx-7。令cosx=t,则t∈[-1,1],所以原函数等价于函数f(t)=t2+4t-7。

因为二次函数f(t)=t2+4t-7关于直线t=-2 对称,且图像的开口向上,所以函数f(t)=t2+4t-7在t∈[-1,1]上单调递增,所以ymin=f(-1)=(-1)2+4×(-1)-7=-10,ymax=f(1)=12+4-7=-2,所以原函数的值域为[-10,-2]。应选D。