转化与化归思想在函数中的应用

■张卫青

应用1:利用转化与化归思想解决不等式问题

例1 若实数x,y满足2020x-2020y<2021-x-2021-y,则( )。

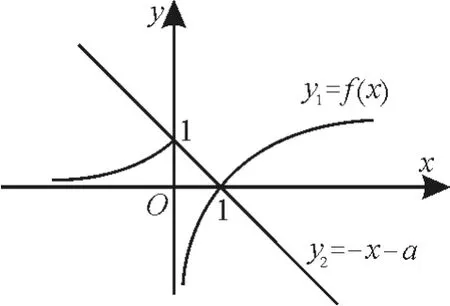
分析:构建函数f(x)=2 020x-2021-x,结合单调性得x

解:因为2020x-2020y<2021-x-2021-y,所以2020x-2021-x<2020y-2021-y。

升华:对于多个变量的不等式求解问题,可以对不等式进行适当的变形,将其转化为熟悉的函数的单调性问题求解。在解答数学问题时,有时会遇到陌生的问题,感到棘手,这时,可以想办法把陌生的问题和学过的知识联系起来,把陌生的问题转化为熟悉的问题,使所求问题得到有效解决。

应用2:利用转化与化归思想解决函数的最值问题

例2 当x> -1 时,关于代数式下列说法正确的是( )。

A.有最小值 B.最值不确定

C.有最大值 D.无最大值

升华:求形如一次函数或二次函数的代数式最值问题,可以对代数式的分母进行适当的变形,将其转化为熟悉的基本不等式求最值。

应用3:利用转化与化归思想解决函数的零点问题

例 3 已 知 函 数f(x) =g(x)=f(x)+x+a,若g(x)存在两个零点,则a的取值范围是( )。

A.[-1,0) B.[0,+∞)

C.[-1,+∞) D.[1,+∞)

分析:令g(x)=0,可得f(x)=-xa,则原问题等价于函数y1=f(x)与y2=-x-a的图像有两个交点,画出两个函数的图像即可求解。

解:令g(x)=f(x)+x+a=0,则方程f(x)=-x-a有两个根,即函数y1=f(x)与y2=-x-a的图像有两个交点。画出函数y1=f(x)与y2=-x-a的图像,如图1 所示。

由图可知,当y2=-x-a的纵截距-a≤1,即a≥-1 时,函 数y1=f(x)的图像与直线y2=-x-a有两个交点,所以a∈[-1,+∞)。应选C。

升华:研究函数的零点问题时,若发现函数的零点很难求,则可以把它转化为两个函数图像的交点问题。对于函数的零点,大部分问题的解决都离不开转化与化归和数形结合思想。

应用4:利用转化与化归思想判断大小

例4 已知55<84,134<85,设a=log53,b=log85,c=log138,则( )。

A.a

C.b

分析:结合中间值即可比较大小。

综上可得,c>b>a。应选A。

升华:对数的比较大小问题,若无法借助中间值比较大小,则可以将对数转化为同底的对数,然后比较大小。题中利用这一关系,体现了转化思想的应用。

应用5:利用转化与化归思想解决恒成立问题

例5 已知函数f(x)=x2-4x+a,g(x)=ax+5-a,若对任意的x1∈[-1,3],总 存 在x2∈[-1,3],使 得f(x1)=g(x2)成立,则实数a的取值范围是( )。

A.(-∞,-9]

B.[- 9,3]

C.[3 ,+∞)

D.(-∞,-9]∪[3 ,+∞)

分析:对任意的x1∈[-1,3],总存在x2∈[-1,3],使得f(x1)=g(x2)成立,可转化为f(x)在[-1,3]上的值域是g(x)在[-1,3]上值域的子集。这里f(x)和g(x)都是熟悉的函数,只需讨论a在不同取值时f(x)和g(x)的取值。

解:对任意的x1∈[-1,3],总存在x2∈[-1,3],使得f(x1)=g(x2)成立,即f(x)在[-1,3]上的值域是g(x)在[-1,3]上值域的子集。

因为f(x)=(x-2)2+a-4 的图像的开口向上,且对称轴为x=2,所以在[-1,3]上的值域为[a-4,a+5]。

对于函数g(x)=ax+5-a,当a<0时,g(x)在[-1,3]上的值域为[2a+5,5-2a],此时解得a≤-9;当a=0时,g(x)在[-1,3]上的值域为{5},不满足要求;当a>0 时,g(x)在[-1,3]上的值 域 为 [5- 2a,2a+ 5], 此 时解得a≥3。

综上可得,a的取值范围是(-∞,-9]∪[3,+∞)。应选D。

升华:对于恒成立问题,可以转化为值域问题,通过研究函数的值域,使问题得到解决。恒成立问题和函数零点问题类似,恒成立问题的解决离不开转化与化归和数形结合思想。

提示:只需f(x)min≤g(x)max。易得实数a的取值范围是[-3,+∞)。