New indices to balance α-diversity against tree size inequality

Li Zhang · Brady K.Quinn · Cang Hui ·Meng Lian · Johan Gielis · Jie Gao · Peijian Shi

Abstract The number and composition of species in a community can be quantified with α-diversity indices,including species richness (R),Simpson’s index (D),and the Shannon–Wiener index (H΄).In forest communities,there are large variations in tree size among species and individuals of the same species,which result in differences in ecological processes and ecosystem functions.However,tree size inequality (TSI) has been largely neglected in studies using the available diversity indices.The TSI in the diameter at breast height (DBH) data for each of 999 20 m × 20 m forest census quadrats was quantified using the Gini index(GI),a measure of the inequality of size distribution.The generalized performance equation was used to describe the rotated and right-shifted Lorenz curve of the cumulative proportion of DBH and the cumulative proportion of number of trees per quadrat.We also examined the relationships of α-diversity indices with the GI using correlation tests.The generalized performance equation effectively described the rotated and right-shifted Lorenz curve of DBH distributions,with most root-mean-square errors (990 out of 999 quadrats) being <0.0030.There were significant positive correlations between each of three α-diversity indices (i.e.,R,D,and H’) and the GI.Nevertheless,the total abundance of trees in each quadrat did not significantly influence the GI.This means that the TSI increased with increasing species diversity.Thus,two new indices are proposed that can balance α-diversity against the extent of TSI in the community: (1 -GI) × D,and (1 -GI) × H’.These new indices were significantly correlated with the original D and H΄,and did not increase the extent of variation within each group of indices.This study presents a useful tool for quantifying both species diversity and the variation in tree sizes in forest communities,especially in the face of cumulative species loss under global climate change.

Keywords Diameter at breast height (DBH) · Gini index ·Shannon–Wiener index · Simpson’s index · Quadrat · Tree size

Introduction

Indices of α-diversity are used to quantify species diversity within a defined region or community (Whittaker 1960).There are three commonly used α-diversity indices: (1)species richness (R),which denotes the number of species within a region or community;(2) Simpson’s index (D),which reflects the probability that two randomly selected individuals belong to the same species (Simpson 1949);and (3) the Shannon–Wiener index (H’),which is used to quantify the chance of choosing an individual of a dominant species at random (Shannon 1948).However,these indices do not necessarily capture the functional structure of a forest that largely reflects variations in nutrient cycling,photosynthetic capacity,competitive dominance,and vital rates among different sized trees.

Tree size distribution in natural forests and plantations is a fundamental feature of forest structure (Des Roches et al.2017).In a single-or multi-species forest,there exists at least some variation in tree size (Lai et al.2013;Cohen et al.2016;Liu et al.2016,2020),which reflects the competitive dynamics and community succession processes resulting from climatic and geographical variables (Piponiot et al.2022).Thus,a community with greater tree size inequality(TSI) can effectively be considered as actually less “diverse”than one with equal numbers of trees and species with a more even distribution of sizes.Therefore,it is useful to quantify TSI within a community to discover the influence of species diversity on inter-and intraspecific competition and adaption of species to their environments.This might reflect another aspect of competitive dominance,productivity limits,and/or a lack of functional diversity within the community.In addition,TSI also reflects differences in photosynthetic capacities,carbon capture,and carbon storage ability among forests with the same species diversity levels.In contrast,the demographic equilibrium theory assumes size-dependent growth,mortality,and recruitment,and has been shown to be capable of more precisely explaining tree-size distributions than the metabolic theory (Muller-Landau et al.2006;Moore et al.2018).Therefore,TSI can contribute to a combined index of species and functional diversity that would be missed by using conventional indices.Prior studies have demonstrated that increasing species diversity increases the stability of community productivity but decreases the stability of individual species productivity (Lehman and Tilman 2000;Tilman et al.2014).TSI is thus a good measure of the variation in forest productivity.Although previous studies have shown that population density and forest age structure can significantly affect the TSI(Taylor and Aarssen 1989;Metsaranta and Lieffers 2008),it is still unknown whether species diversity in a community affects TSI,although based on the above there should be a trade-off between species diversity and TSI.

The Lorenz curve is used in economics to represent income inequality in a given region as the bivariate plot of the cumulative proportion (or cumulative percentage)of household income vs.the cumulative proportion (or cumulative percentage) of households (Lorenz 1905).The quotient of the area between the Lorenz curve and the 45°straight line (denoted as the line of absolute equality) to 0.5 (i.e.,the area of the triangle formed by the 45° straight line,thex-axis,and the straight line ofx=1) is referred to as the Gini index (GI).If the number of data points is not sufficiently large,the use of some mathematical equations to describe the Lorenz curve is recommended to maintain the curve’s smoothness (e.g.,Gastwirth 1972;McDonald 1984;McDonald and Xu 1995;Chotikapanich and Griffiths 2002;Lian et al.2023).The numerical value of the GI ranges from 0 to 1,and the larger the GI value,the more unequal the household income distribution in a region of interest;if the Lorenz curve overlaps with the line of absolute equality,the GI equals 0.The Gini index has previously been applied to measure the inequality of plant size (e.g.,tree volume,height,diameter at breast height) or plant organ size (fruit and seed size) (Taylor and Aarssen 1989;Metsaranta and Lieffers 2008;Chen et al.2014).However,no study has yet examined whether species diversity can influence the GI of tree size distributions (or vice versa).In addition,the available α-diversity indices only consider the number and composition of species in a community.If species diversity has a significant influence on the TSI,which itself impacts forest functional diversity,productivity,and stability,then it is more reasonable to develop some new indices that can capture/account for the trade-off between species diversity and variation in tree size within a community.

In the present study,we used the species occurrence data for 999 20 m × 20 m quadrats from a temperate forest census.We calculated the GI values of the DBH distribution as a representative tree size distribution,given that the DBH can be more accurately measured than height using the protocols proposed by Lian et al.(2023).We then calculatedR,D,andH’ to test whether species diversity significantly affected the GI,and proposed two new indices that can balance species diversity against the TSI based onDandH’.

Materials and methods

Forest census data

A forest census dataset previously collected within a 400 m × 1000 m study region was used,which consisted of 1000 20 m × 20 m quadrats in Beijing Songshan National Nature Reserve,China (40°30′50″ N,115°49′12″ E) and sampled in August 2014 (see Shi et al.2018) for details;data accessible in Shi et al.(2023).Scientific names and DBH of all trees with DBH ≥ 1 cm were recorded.There was only one quadrat without trees among the 1000 quadrats.Figure 1 shows the species distribution in one of the 999 quadrats.

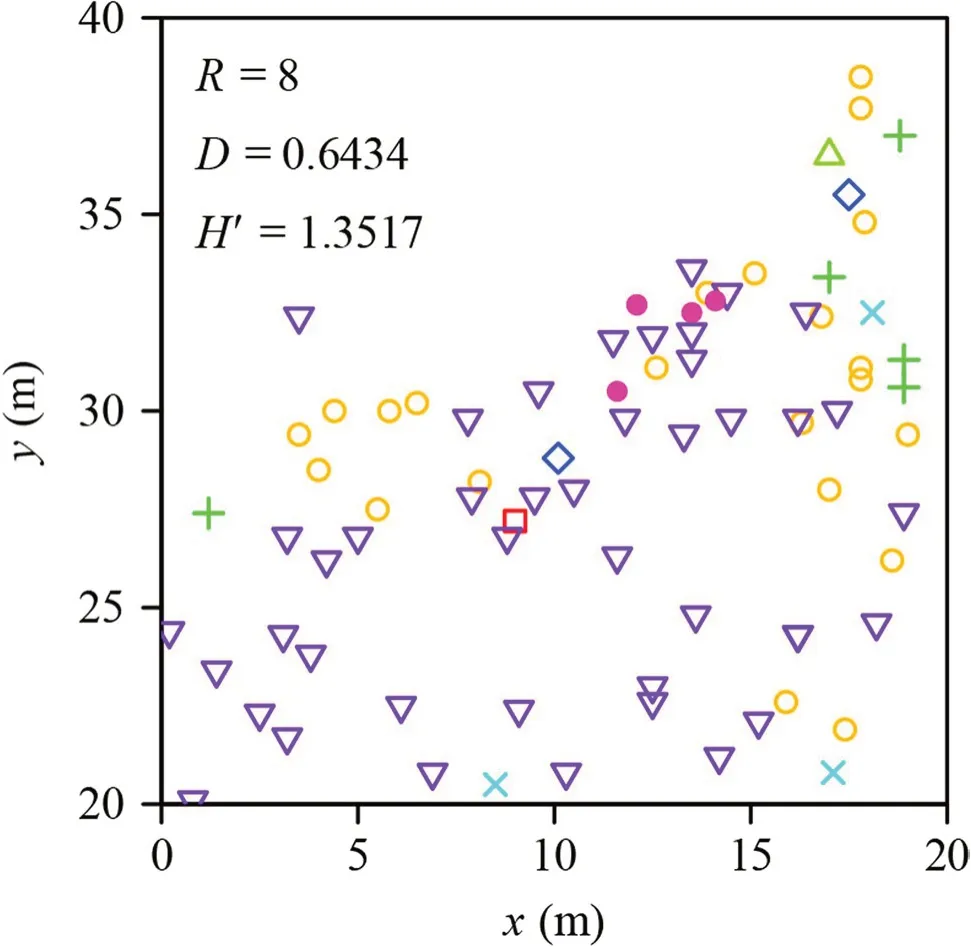
Fig.1 The spatial distribution of trees in a 20 m × 20 m quadrat randomly selected from among the 999 quadrats with trees in the study in Beijing Songshan National Nature Reserve censused in August 2014.x and y are the horizontal and vertical axes of the quadrat (m);symbols represent locations of different tree species on the coordinate plane;R is species richness,D Simpson’s index,and H’ the Shannon–Wiener index

Calculation of α-diversity indices

Species richness (R) is the number of species present in a quadrat.Simpson’s index (D;Simpson 1949) and the Shannon–Wiener index (H’;Shannon 1948) of a quadrat are calculated by:

respectively,wherepirepresents the abundance of thei-th species as a proportion of the total abundance of all species across the quadrat.

Performance equation and parameter estimation

The performance equation was initially proposed to describe the effect of temperature on the jumping distance of a frog,i.e.,animal behavior performance (Huey and Stevenson 1979),and was demonstrated to be valid for use in describing temperature-dependent development rates of insects (Shi et al.2011;Wang et al.2013).Lian et al.(2023) found that a generalized version of the performance equation could be generated after rotating the Lorenz curve of the cumulative proportion of leaf size (leaf area or leaf dry mass) vs.the cumulative proportion of number of leaves per culm by 135°counterclockwise and shifting it to the right by a distance of√2.The generalized performance equation was therefore used to fit the rotated and right-shifted Lorenz curve of the cumulative proportion of DBH (representing tree size) vs.the cumulative proportion of number of trees in a quadrat:

whereyandxare the rotated and right-shifted Lorenz curve of the cumulative proportion of DBH vs.the cumulative proportion of number of trees per quadrat,respectively;a,b,c,K1,andK2are parameters to be estimated.Figure 2 shows the original Lorenz curve,and the rotated and rightshifted Lorenz curve.Whena=b=1,Eq.(3) reduces to the non-generalized performance equation (Huey and Stevenson 1979):

The parameters in the generalized performance equation were estimated using nonlinear least squares based on the Nelder-Mead optimization algorithm (Nelder and Mead 1965) to minimize the residual sum of squares (RSS)between the observed and predictedyvalues.The rootmean-square error (RMSE) reflected the goodness of fit of the generalized performance equation:

wherenrepresents the total abundance of all tree species in a quadrat.

Gini index for tree size distribution and two extended Gini-alpha-diversity indices

The Gini index (GI) is defined as:

whereyfollows Eq.(3).Based on the parameters estimated using the generalized performance equation fit to the rotated and right-shifted data of the cumulative proportion of DBH vs.the cumulative proportion of number of trees per quadrat,the GI values of DBH distribution for 999 quadrats were obtained.Based on Eq.(6),two extended indices are proposed that weight the species index diversity values by the extent of TSI (i.e.,reduce the diversity index value when the GI value is higher),i.e.,the Gini-Simpson index (DGI)and the Gini-Shannon–Wiener index (H′GI):

Fig.2 The original Lorenz curve and the rotated and right-shifted Lorenz curve of the example quadrat illustrated in Fig.1.(A) is the fitted Lorenz curve with observations,where letters with ^ represent the estimated values of the parameters of the generalized performance equation;RMSE is the root-mean-square error;the Gini index is the ratio of the area of the gray region (i.e.,the area formed by the Lor-enz curve and the 45° straight line that represents the line of absolute equality) to 1/2.(B) is the Lorenz curve rotated 135° counterclockwise and shifted to the right by a distance of√2.The points are observations,and the red lines are values predicted by the generalized performance equation

The statistical softwareR(version 4.2.0;R Core Team 2022) was used to carry out calculations and create figures,and the "IPEC" package (version 1.0.3;Shi et al.2022) was used specifically to estimate the parameters of the generalized performance equation.

Results

The RMSE values of 990 of the 999 quadrats were smaller than 0.0030,and all were under 0.0050 (Table S1),which demonstrated the validity of the generalized performance equation as used (Fig.3).The GI had no significant correlation with the total abundance of tree species per quadrat(P>0.05),whileR,D,andH’ were significantly positively correlated with the GI (P<0.001) (Fig.4;Table S1).Relative to the originalDandH′,the new indices DGI anddid not show greater variation in their frequency distributions (Fig.5),and the introduction of the GI to the α-diversity indices did not lead to serious deviation from the traditional α-diversity indices ofDandH′,given the significant positive correlations betweenDand DGI,and betweenH’ and(Fig.6).

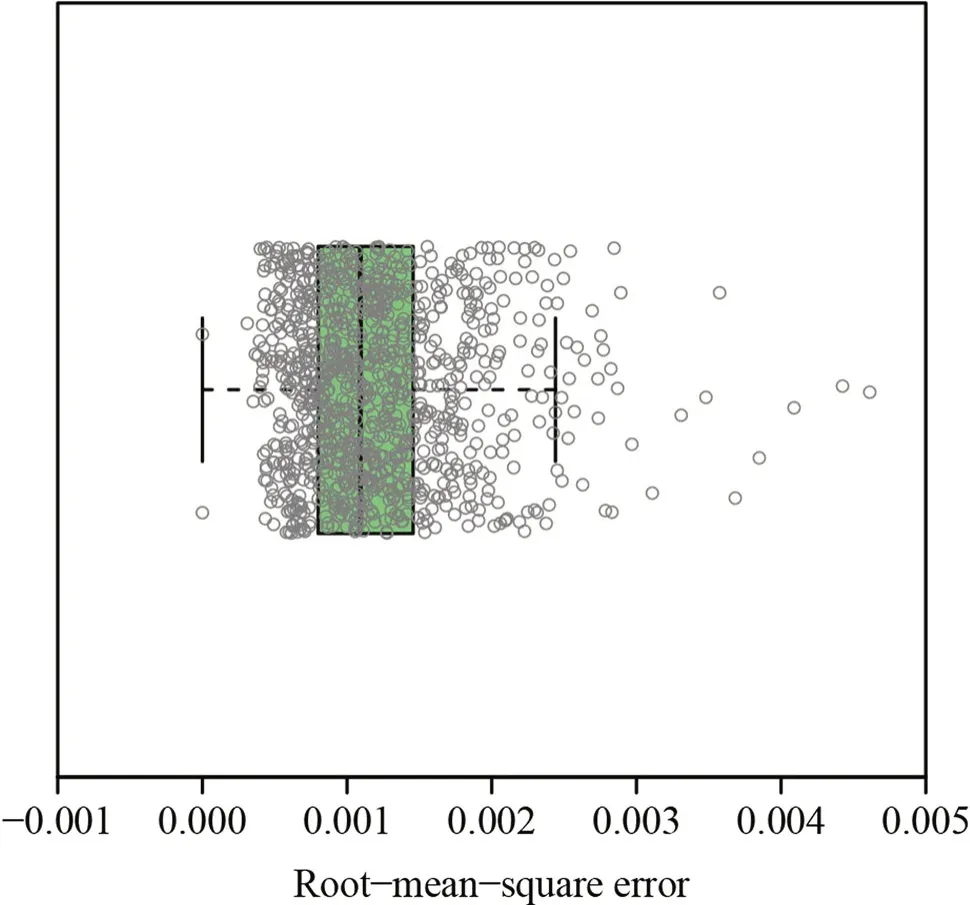
Fig.3 Root-mean-square errors obtained using the generalized performance equation to fit the rotated and right-shifted data of the cumulative proportion of DBH vs.the cumulative proportion of number of trees per quadrat for the 999 20 m × 20 m quadrats

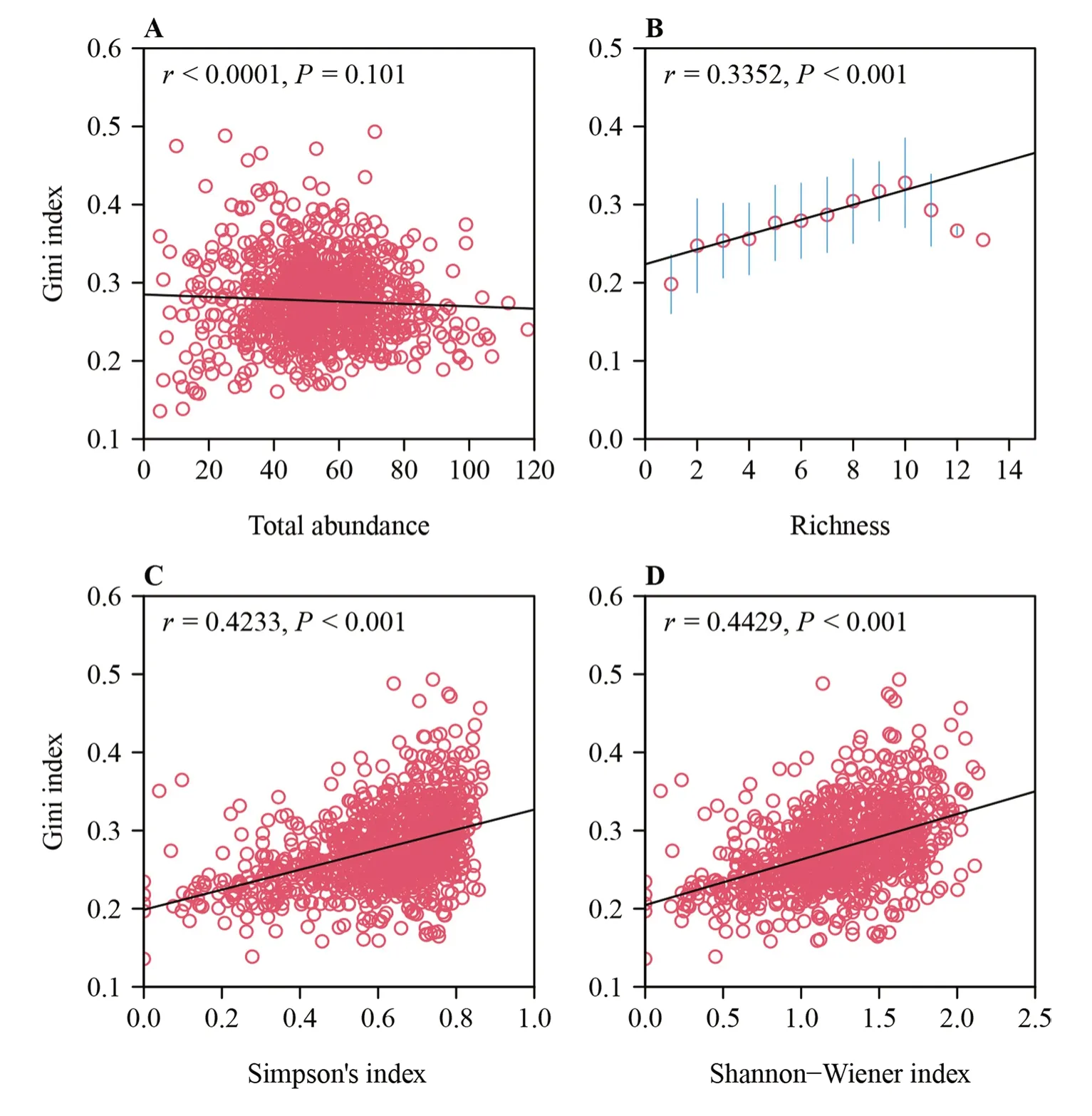
Fig.4 Correlations between species diversity indices and the Gini index of DBH distribution for each quadrat.(A) Gini index versus total abundance;(B) Gini index versus species richness;(C) Gini index versus Simpson’s index;and (D) Gini index versus the Shannon–Wiener index.Data points represent 999 20 m × 20 m quadrats of census data.In (B),open circles and vertical bars represent means and standard errors of GI indices at different species richness values.In all panels,r is the correlation coefficient,and P the P-value of the correlation test

Fig.5 Boxplots of Simpson’s index (A),Shannon–Wiener index (B),Gini-Simpson index(C),and Gini-Shannon–Wiener index (D) distributions across all 999 quadrats.The extent of variation in each index’s values was evaluated using the coefficient of variation (CV=SE/Mean × 100%),where "SE"and "Mean" are the standard error and mean of each group of index values,respectively

Fig.6 Correlations between Simpson’s index and Gini-Simpson index,and between the Shannon–Wiener index and Gini-Shannon–Wiener index.Open circles represent 999 20 m × 20 m quadrats of census data;r is the correlation coefficient,and P the P value of the correlation test

Discussion

This section largely focused on: (1) whether there are better measures to replace DBH as a representative of tree size;(2) the value of using the Gini index (GI) to measure tree size inequality (TSI) in a community;and (3) the correlation between species diversity and the TSI quantified by the GI.

Representatives of tree size

Although DBH does not perfectly quantify size,e.g.,volume is usually approximately proportional to the DBH2× height(Singh and Singh 2001),previous studies have used DBH as a representative of tree size for convenience (e.g.,Wyckoff and Clark 2005).In fact,height has an allometric relationship with DBH (Zhang 1997;Sumida et al.2013).Regardless of interspecific differences in numerical parameter values (Zhang 1997),tree height can be represented as a nonlinear function of DBH.Given this,then size (e.g.,aboveground volume,mass or crown volume) can be represented by DBH using parametric or non-parametric models.Nevertheless,measuring tree size using one variable,DBH,rather than using both height and DBH may lead to greater deviation in size distributions.When examining the photosynthetic capacity of a forest community,the crown volume or surface area of each tree might be more meaningful than tree size.With the development of drone-based LiDAR(light detection and ranging) technology and its application in forestry,it is becoming easier to obtain crown metrics(Silva et al.2016;Ahongshangbam et al.2020).It may be promising in the future to calculate the GI of the crown volume or surface area distribution for different tree species in a community.In practice,we could also choose to calculate the projection area of a crown to represent its surface area using two vertical directions of crown length (e.g.,defining the distance in the east–west direction as the crown length,and in the north–south direction as the crown width).For the projection shapes of tree crowns,it is recommended that the LiDAR measurement and the conventional eight-point crown projection be used (Fleck et al.2011).However,the Montgomery equation that assumes the area of a planar object is proportional to the product of the object’s length and width,and whose validity in leaf area calculation has been demonstrated for a large number of broad-leaved plants with diverse leaf shapes (Shi et al.2019;Yu et al.2020;Schrader et al.2021),is also applicable to the calculation of crown projection area.This will be simpler than the previous two methods to calculate the GI for quantifying the inequality of the photosynthetic capacities,as denoted by the crown projection area among individual trees in a quadrat.

Demographic equilibrium of size-dependent recruitment

If one assumes a quadrat to be a local community,then the sum of DBH of all trees per quadrat can be considered as the community productivity.The Gini index of DBH distribution is therefore indicative of the demographic equilibrium of size-dependent growth and recruitment in a community(Muller-Landau et al.2006;Moore et al.2018) because it is positively correlated with the coefficient of variation (CV=SE/Mean) of DBH per quadrat (r=0.96,andP<0.001;Fig.7).The CV in DBH per quadrat has been argued to reflect the stability of individual species productivity (Tilman et al.2014),so the larger the CV,the more uneven is individual species productivity.Thus,a large GI indicates a community lacking demographic equilibrium.Consequently,the GI quantifies the TSI per quadrat,and reflects the demographic equilibrium of size-dependent recruitment (such as productivity and mortality) given the significant correlation between the GI and CV.With increasing species richness,the GI tends to increase (Fig.4B),which suggests that the stability of the individual species productivity in the quadrat tends to decrease with increasing species diversity (Landi et al.2018).This is in accordance with the predictions based on a model of resource competition in a temporally fluctuating environment (Lehman and Tilman 2000;Tilman et al.2014).As a result,the GI and(1-GI) both range from 0 to 1 and can serve as weights to balance against the available α-diversity indices by the TSI.

Fig.7 Correlation between the Gini index and coefficient of variation of the tree size distribution for each quadrat.Open circles represent 999 20 m × 20 m quadrats;r is the correlation coefficient and P the P value of the correlation test

Influence of species diversity on the Gini index of tree size distribution

In this study,the greater the species diversity per quadrat (apart from total abundance),the larger the GI of size distribution.However,total abundance had no significant influence on the GI because the interspecific variation in tree size is usually greater than the intraspecific variation in forest communities (Des Roches et al.2017;Liu et al.2020).The GI increases with increasing species richness(Fig.4B).Huang et al.(2023) calculated the GI values of leaf area distribution for 240 individual plants ofShibataea chinensisNakai,a drought-tolerant dwarf bamboo growing in southern China that usually has 10 -40 leaves per plant,and found that the GI increased as the number of leaves per plant increased but had no significant correlation with the total leaf area per plant.Our results are similar;total species abundance per quadrat is similar to total leaf area per plant,and species richness per quadrat is similar to the number of leaves per plant.The data indicate that species richness has more influence on TSI than the density of any given species.Consequently,the two proposed indices consider the extent of TSI and balance it against the α-diversity.This is necessary for describing the structural diversity of a forest besides just compositional diversity.In the present study,(1 -GI)was used as a weight to balance α-diversity against tree size inequality.In light of differences among types of forests and biomes,an additional non-negative parameter,d,could be added as the power of (1 -GI) in Eqs.(7) and (8),i.e.,

In this case,the influence of different types of forests and biomes can be reflected by the parameterdto a certain extent,which is helpful when comparing species diversities across different climatic regions or biomes.

Conclusions

We used 999 20 m × 20 m quadrats of forest census data and calculated the Gini index (GI) of DBH distribution per quadrat using the generalized performance equation to fit the rotated and right-shifted data of the cumulative proportion of DBH vs.the cumulative proportion of number of trees per quadrat to reflect tree size inequality (TSI).The generalized performance equation was valid for use in describing the rotated Lorenz curve,as the root-mean-square errors were all <0.0050,and 99% of root-mean-square errors were <0.0030.There was no correlation between the GI and the total abundance per quadrat,but with increasing species diversity,GI significantly increased.Two new indices are proposed based on Simpson’s index and the Shannon–Wiener index by introducing a weight of (1 -GI) to balance species diversity against the TSI.We found that there were significant positive correlations between Simpson’s index and the Gini-Simpson index,and between the Shannon–Wiener index and the Gini-Shannon–Wiener index.This suggests that the two new indices do not conflict with the traditional indices of α-diversity.

AcknowledgementsWe thank Long Chen,Yanhong Liu and Julian Schrader for their valuable help during the preparation of this manuscript.We are also grateful to the three expert reviewers for their constructive comments.

FundingThis work was supported by the National Natural Science Foundation of China (32101260).

Data availabilityThe forest survey data are accessible in Dryad,an online repository,at https:// doi.org/https:// doi.org/ 10.5061/ dryad.h9w0v t4np.Statistics computed for each quadrat in this study are available in the Electronic Supplementary Materials (Table S1).

Open AccessThis article is licensed under a Creative Commons Attribution 4.0 International License,which permits use,sharing,adaptation,distribution and reproduction in any medium or format,as long as you give appropriate credit to the original author(s) and the source,provide a link to the Creative Commons licence,and indicate if changes were made.The images or other third party material in this article are included in the article’s Creative Commons licence,unless indicated otherwise in a credit line to the material.If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use,you will need to obtain permission directly from the copyright holder.To view a copy of this licence,visit http://creativecommons.org/licenses/by/4.0/.