显式算法中三维黏弹性人工边界应用及输水隧洞动力响应分析

2024-01-26陈旻铭任旭华张继勋

水力发电 2024年1期

陈旻铭，任旭华，张继勋

(河海大学水利水电学院，江苏南京210024)

0 引言

随着地下综合管道的加密，既有水工隧洞结构的安全与稳定问题愈加复杂。采用有限元法模拟无限域地基中隧洞的动力响应问题时，人工截断边界单元参数加载的合理性与准确性难以控制。动力人工边界中由于黏弹性人工边界具有克服高频失稳和低频飘移、精度高、实用性强等特点，许多学者对此开展了研究。刘晶波等[1]分析了二维黏弹性人工边界和半无限空间的静力问题的基本解，建立了三维静-动力统一人工边界理论。谷音等[2]基于集中黏弹性边界理论，提出了等效三维一致黏弹性人工边界单元。章小龙等[3]通过Fortran 程序编写命令流的方式，给计算区域批量定义黏弹性边界单元，实现了黏弹性边界理论在ABAQUS/Standard中的运用。在动力分析中，人工边界区的稳定性比内部计算区域的稳定条件更为严格，目前引入黏弹性边界时，多采用隐式的无条件稳定算法。显式算法与之相比效率优势明显，但存在边界参数设置较为复杂且容易发生失稳等问题。李述涛等[4]对此提出在二维黏弹性人工边界近端增加集中质量的方法，提高了动力分析在显式算法中的稳定性。刘晶波等[5]通过求解边界区域子系统的稳定性系数，改善其影响条件，从而提高二维黏弹性边界的稳定性宽容度及计算效率。

本文在总结前人研究的基础上，提出一种适用于动力显式计算的三维黏弹性人工边界施加方法，并依托某输水隧洞与临近高铁隧道的立交工程，在设有三维黏弹性边界的基础上，研究高速列车振动荷载对既有水工隧洞的振动影响特性与规律。

1 动力显式中黏弹性人工边界的实现

1.1 三维黏弹性人工边界系数的建立

黏弹性人工边界是一种设置在人工截断面节点上的弹簧阻尼系统，用以吸收计算模型向边界辐射的能量。为了改善黏弹性人工边界在显式动力分析中的逐步积分稳定性，本文参考文献[6]稳定性改善方法，推导了三维黏弹性人工边界的稳定性改善公式，建立整个模型的人工边界子系统，包括：①顶角子系统、②棱边子系统和③侧面子系统。布置形式见图1。图1中，MB为边界节点的集中质量系数。

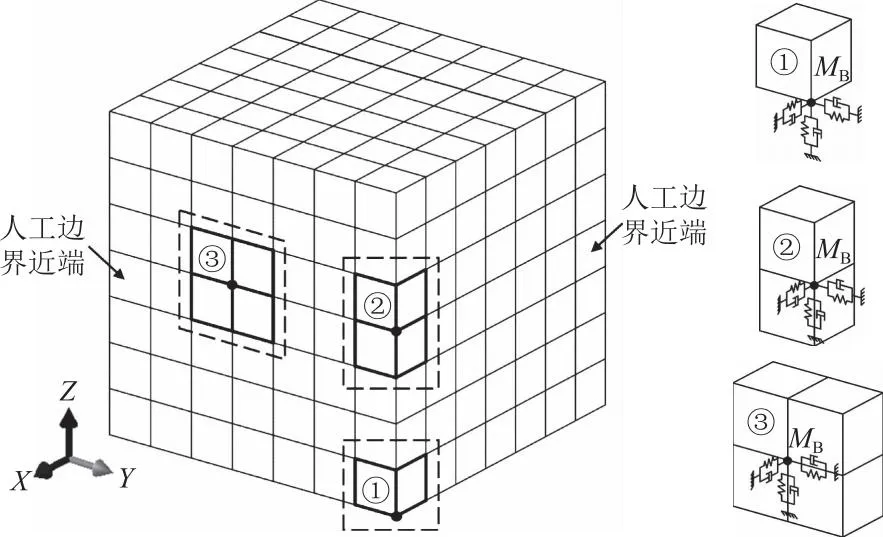
图1 人工边界子系统

三维时域下，黏弹性人工边界的稳定性改善以中心差分方法[7]为基础，逐步积分递推公式如下

(1)

U(t+Δt)=A·U(t)+P(t)

(2)

式中，U为复合矩阵；A为人工边界子系统的传递矩阵；P为外力向量。U的具体表达式为

(3)

由文献[3]可知，子系统的稳定性积分与向量P无关，实则是求解传递矩阵A的谱半径。此时，边界稳定性判别条件ρ(A)=max|λi|的取值应在[-1，1]之间(λi为传递矩阵的特征值)，即当λi的模不大于1时，积分格式满足稳定性条件。临界时间步长为

(4)

式中，γ为边界子系统的稳定性系数；L为有限单元的最小边长；cP为压缩波波速。改善后人工边界上的弹簧刚度与阻尼系数与改进前相同，人工边界近端的集中质量系数MB取值为

(5)

式中，βB为黏弹性人工边界质量参数。结合文献[2]中三维黏弹性边界系数的递推思路可知，当βB≥3ρL/2时，三维边界子系统的稳定性系数均大于内部区域，即模型的稳定性仅由内部区域决定，临界时间步长可通过改善内部区域的单元条件来提高；ρ为质量密度。因此，三维黏弹性边界系数的计算公式可表示为

(6)

式中，KBT1、KBT2和KBN为第一切向、第二切向和法向的弹簧的刚度系数；CBT1、CBT2和CBN为阻尼元件第一切向、第二切向和法向的阻尼系数；MBT1、MBT2和MBN为边界节点第一切向、第二切向和法向的集中质量系数；αT1、αT2和αN为黏弹性边界第一切向、第二切向和法向的修正系数，三维取值参考李金友[8]等研究，取法向αN=1.3，切向αT1=αT2=0.7；G为岩土体的剪切模量；R为黏弹性边界节点到轨道中心线或固定波源的最短距离；cS为剪切波的波速。cP和cS可表示为

(7)

(8)

式中，E为弹性模量；μ为泊松比。

1.2 黏弹性人工边界施加

在计算黏弹性人工边界的弹簧刚度、阻尼及附加质量时，将式(6)中的各系数乘以节点控制面积[9]即可。在ABAQUS/Explicit模块，动力隐式阶段设置的接地弹簧将会失效，此时需要重新定义接地端节点。将人工边界的所有节点分别沿X、Y、Z轴复制并移动一段距离，作为动力显式计算的远端节点，设置远端节点的Point mass/inertia，并将节点完全固定，使其等价于接地端，最后在远端节点与原人工边界的近端节点之间通过ABAQUS设置Springs/Dashpots单元即可，批量处理可通过Matlab程序完成。远端节点的设置与黏弹性边界施加见图2。ABAQUS显式动力分析中黏弹性边界加载的整体过程见图3。

图2 远端节点的定义与黏弹性边界的施加

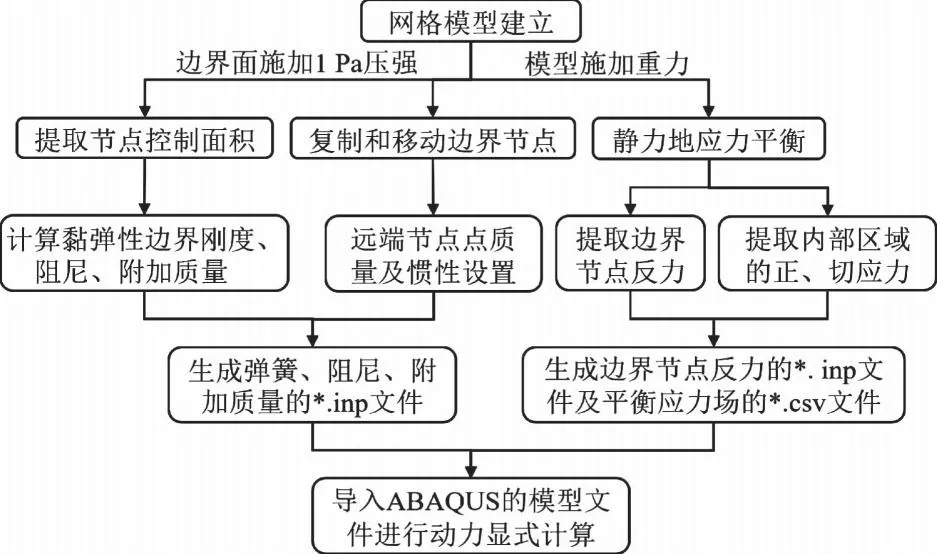
图3 ABAQUS显式计算流程

1.3 黏弹性人工边界验证

建立尺寸为50 m×50 m×100 m三维模型，见图4。图4中，A、B、C点分别为模型的顶面中心、几何中心和底面中心。采用各边边长为5 m的单元离散，顶面为自由边界面，其他面均为黏弹性人工边界面。土体质量密度为2 000 kg/m3，弹性模量为208 MPa，泊松比为0.3。从底部边界垂直入射1个前进方向沿Z轴的P波和1个前进方向沿X轴的SV波，P波和SV波的振动方向均为Z轴正向，持时0.25 s，其波形见图5。由式(7)和(8)计算cP和cS分别为374.17、200 m/s。

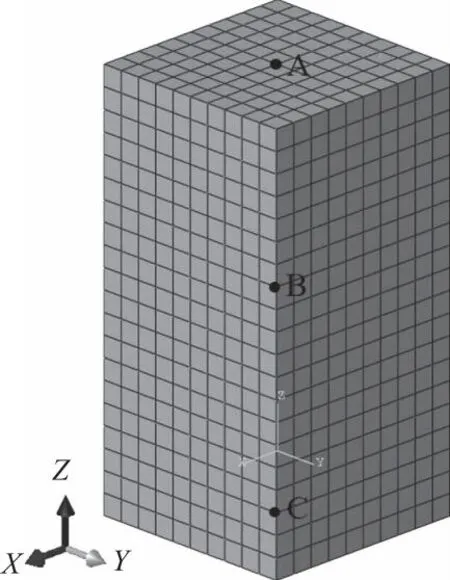
图4 显式黏弹性边界验算模型

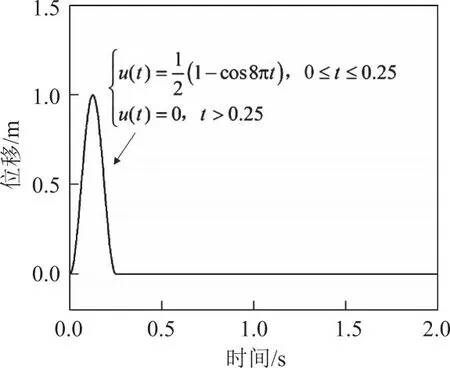
图5 振动波位移曲线

图6给出了显式计算的振动波位移数值解。从图6可知，P波、SV波分别在0.27、0.25 s时到达A点，经过自由面反射后向下传播，分别于0.53、0.50 s时回到C点，0.78、0.75 s后，P波、SV波完全穿过模型底部并向无限远处区域传播，不再向上反射。振动波在A点的最大位移是B、C点的2倍，与文献[10]中隐式求解的脉冲波位移时程曲线的变化规律完全一致，说明人工边界具有良好的吸能效果，满足远域地基弹性恢复的性能，同时也说明了上述的黏弹性人工边界在显式求解中具有的稳定性，有效地削弱了波在传递过程中的振动叠加效应[11]。

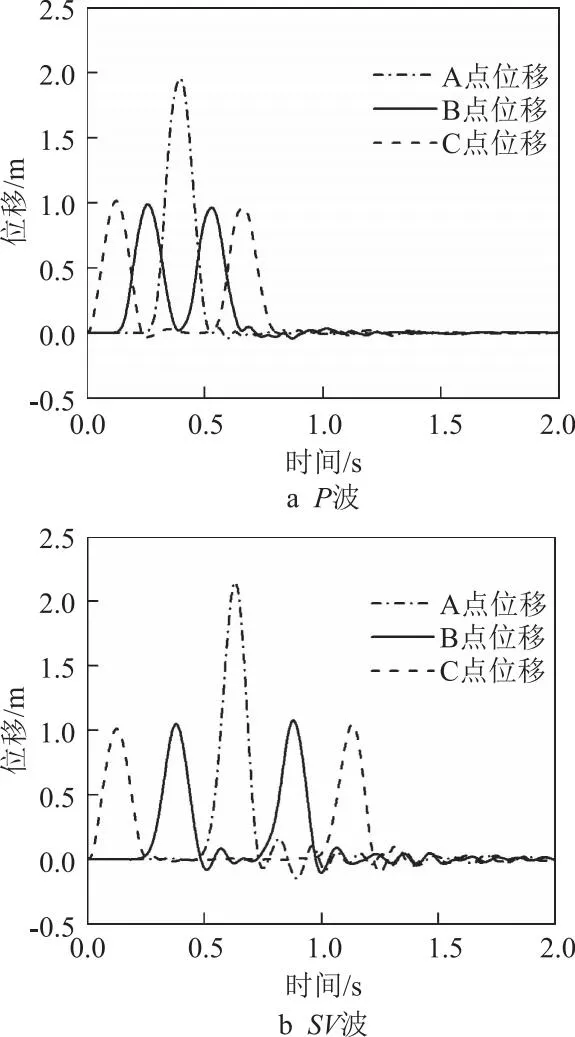
图6 振动波位移时程数值解

2 输水隧洞动力响应分析

2.1 动力计算模型及材料参数

以某输水隧洞与高铁隧道的立体交叉工程为例，研究高铁振动荷载对既有输水隧洞的动力响应。上行线为马蹄形无压隧洞，净断面尺寸7.4 m×7.4 m，衬砌厚0.4 m，拱顶埋深40.3 m；下穿线为双洞单线的列车隧道，内侧直径5.5 m，衬砌厚0.35 m。2条隧道中心线的间距为12.5 m，交叉洞线以90°立交，竖向最小净距5.4 m，交叉段为Ⅳ级围岩。截取三维模型的尺寸为90 m×85 m×85 m，见图7。

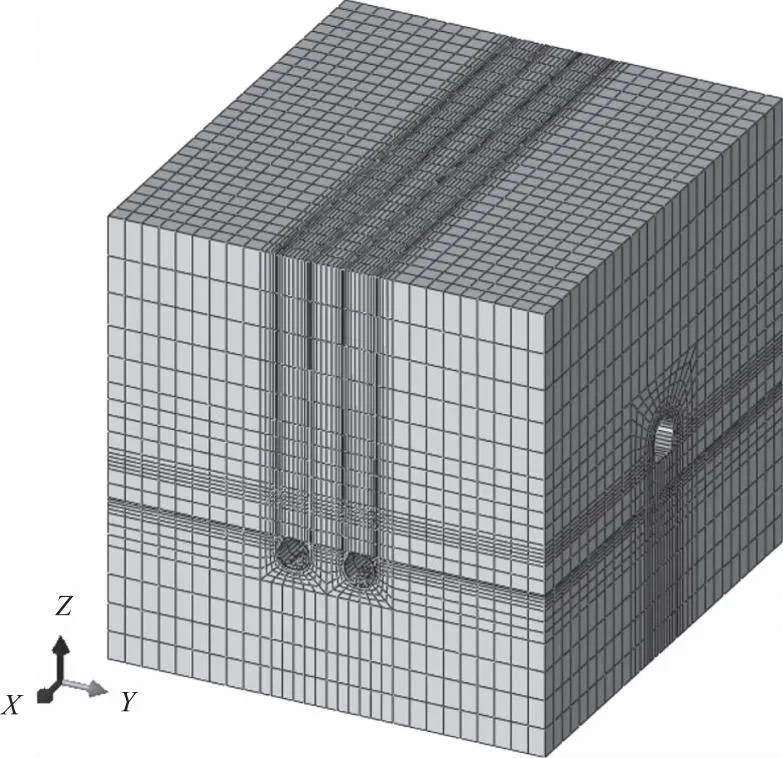
图7 交叉隧洞整体结构

数值计算仅考虑最不利工况，即下穿隧道左右线并排通行同向列车对输水隧洞运行期的动力响应。列车最高时速为350 km/h，无压输水隧洞运行期水深约5 m，振动会导致水体对衬砌产生较大的作用，动水压力参考文献[12]以附加质量的形式施加。输水隧洞监测断面见图8。观测点布置见图9。模型材料参数见表1。

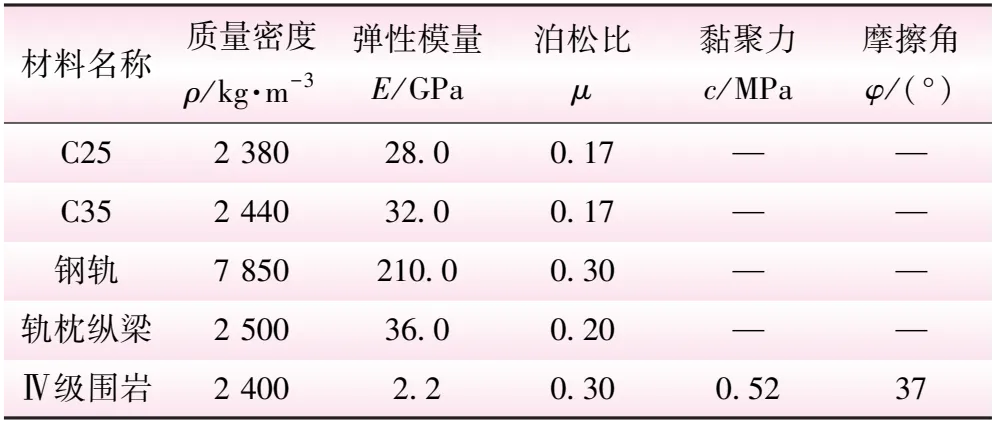
表1 交叉隧洞材料参数

图8 输水隧洞计算断面

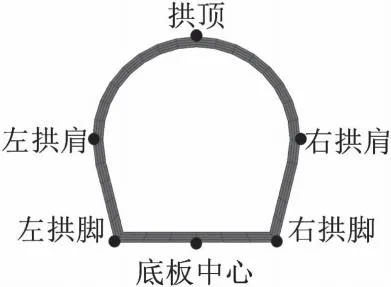
图9 输水隧洞测点布置

2.2 振动荷载模型建立

轨道结构与列车既是组合体也是离散体，振动与轮轨不平顺有关，可以归纳为：①轨道几何不平顺；②轨下基础欠缺；③悬挂与车轴发生竖向相对运动。英国铁路技术中心通过诸多理论与试验分析了轨道随机不平顺与轨面局部波形磨损，对于时速200 km/h的列车建立轨道不平顺管理标准，见表2[13]。

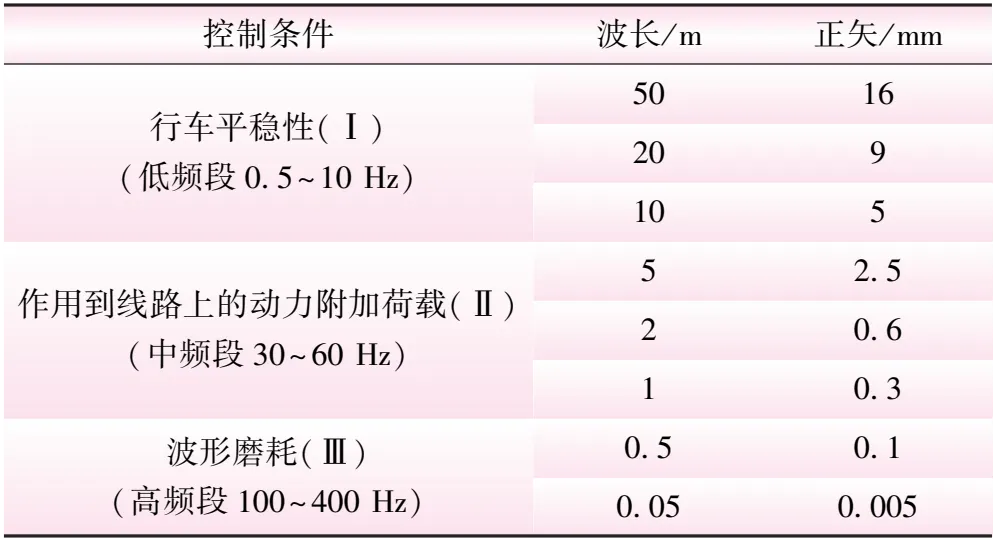
表2 英国轨道不平顺管理值

梁波等[14]考虑轨道行驶的车轮间存在振动叠加现象与荷载在轨道上传递的分散性因素，提出了列车激振力函数F(t)表达式，即

F(t)=k1k2(f0+f1sin(ω1t)+f2sin(ω2t)+f3sin(ω3t))

(9)

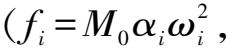
以CRH3型车为例，列车单边轴重8.5 t，簧下质量M0取750 kg。式(9)的函数应用在时速较高的列车上时，其振动荷载会出现负值现象，不符合列车-轨道耦合模型。于鹤然等[15]对此分析了轨面不平顺波形，将表2中典型矢高进行了40%～60%的折减，得到3种控制条件下的典型波长及相应的正矢，分别为L1=10 m、α1=1.75 mm；L2=2 m、α2=0.2 mm；L3=0.5 m、α3=0.04 mm。当v=350 km/h时，激振力时程函数曲线见图10。

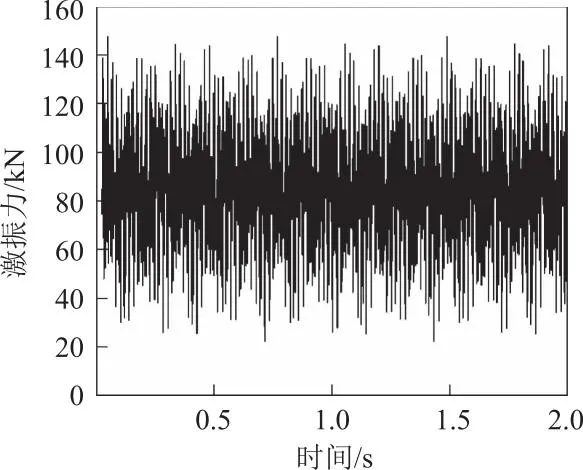
图10 激振力时程函数曲线

车轮荷载的位置和大小都是与时间相关的函数。为提高多轴移动荷载的施加效率，本文结合ABAQUS二次开发功能，采用Fortran程序编写移动载荷。为使该程序便于三维模型的计算，作如下简化：①各节车箱长度、轮对之间的间距均相等；②各节车的单边轴重、簧下质量、车轮作用面积S均相等；③位于两轨道上的同轴车轮的激振力时程完全相同。本文分析的列车由8节车箱编组，单边车轮荷载分布见图11。

图11 高铁列车单边轮荷载分布(单位：m)

2.3 计算结果

振动荷载从驶入模型到完全驶出模型用时3.34 s，各断面测点最大位移见图12。从图12可知，位于轨道左右线中部的S1断面的竖向位移最大，距离右线竖直净距最小的S2断面其次，说明S1断面同时受到左右线振动荷载的影响，其叠加响应效果大于主要受单线影响的S2断面；随着监测断面与右线轨道距离的增加，S3、S4断面的响应程度逐渐减弱，满足振动波在土体介质中传播时发生折减与发散的工程实况。各断面监测点的沉降值由大到小依次为：底板中心>拱脚>拱肩>拱顶。

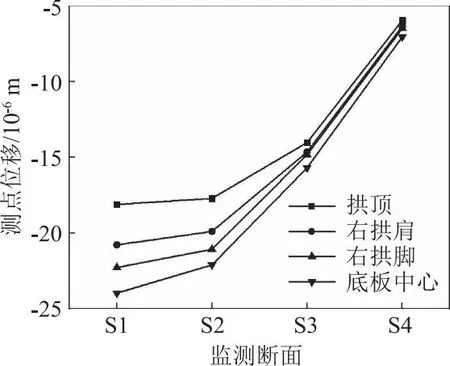
图12 测点最大位移

分析各断面底板中心加速度的响应情况。图13为S1～S4断面的底板中心加速度曲线。从图13可知，S1～S4断面加速度正向极值依次为0.079、0.044、0.024 m/s2和0.002 m/s2，负向极值依次为-0.076、-0.043、-0.024 m/s2和-0.002 m/s2。由此可见，下穿列车对上部输水隧洞的动力响应主要以正向(竖直向上)作用为主，对于S4断面的振动影响极其微弱，说明了黏弹性人工边界充分吸收了振动波能，具有较强的实用性。