基于EEMD-NGO-LSTM神经网络耦合的月径流预测模型及应用

2024-01-26王千凤齐新虎王思宇

水力发电 2024年1期

张冲，王千凤，齐新虎，王思宇，陈末

(1.黑龙江大学水利电力学院，黑龙江哈尔滨150080；2.黑龙江大学寒区地下水研究所，黑龙江哈尔滨150080)

0 引言

准确的径流预测对合理利用水资源、提升防洪减灾能力以及充分发挥水利工程的综合效益具有重要意义[1]。受全球气候变暖的影响，极端降水导致的洪水和干旱等自然灾害频发[2]，严重威胁着农业生产、人民生命和财产安全。因此，精准刻画径流过程和预测未来径流变化对防灾抗灾具有重大的现实意义。然而，径流的形成受到降雨、蒸发、气温等因素影响，各因素之间呈现极复杂的非线性关系，且在时空间分布上也具有一定的不规律性，造成了径流预测的不确定性和不稳定性。

目前，径流预测方法主要为基于物理机制的预测模型和基于统计关系的预测模型[3]。基于物理机制的预测模型需要分析径流的成因，而且模型的结构较为复杂、需要输入大量的水文实测数据、并且模型中参数率定难度较大，预测结果也会随着参数而异，不确定性极高。在实际的水文过程中，有些地方的实测资料由于自然条件恶劣而无法获取，数据量稀少等原因也极大地限制了物理预测模型的使用和预测。基于统计关系的预测模型可以利用各个水文气象要素之间的统计关系，输入历史的水文气象数据就可以对未来的气象要素进行预测，且输入的要素比物理水文模型少得多[4]。目前应用较多的统计预测模型主要有机器学习、时间序列和多元线性回归模型等。机器学习模型例如随机森林[5](RF)、支持向量机[6](SVM)等，一般为黑箱或灰箱模型，过拟合现象严重，而且无法给出明确的解析表达式；时间序列统计模型例如自回归滑动平均模型[7](ARMA)只能反映变量间的线性关系，但不能准确地反映变量间的非线性关系，预测结果在非线性方面精度不高；多元线性回归模型基于预测相关变量和预测变量之间的线性关系来构建模型，对变量间的复杂非线性关系分析不准确。综上所述，目前的模型虽然能做一些相关预测，但都存在一定的缺陷，不能满足径流预报的精度和要求。

因此，相比之下机器学习更具优势，只要加以适当的优化处理就可以达到较好的预测效果。LSTM神经网络属于机器学习的一种，在预测方面得到了广泛应用[8]，目前绝大多数应用LSTM神经网络预测的方式是采用一些数据分解方法对训练数据进行预处理或者采用优化算法对LSTM中的参数进行优化，从而完成较高精度预测。例如宋炜垚[9]使用EEMD方法将径流数据分解为几个相对独立的固有模态函数(IMF)子序列，并对每个子序列分别进行建模，再将得到的子序列输入LSTM神经网络完成了对渭河干流的预测。王立辉等[10]基于灰狼优化算法构建不同的预测模型，较好地完成了丹江口水库月入库径流的预测，纳什系数达到了0.969。刘伟琪等[11]提出了一种由北方苍鹰算法优化的高斯过程回归(GPR)模型，以此模型完成了对大坝变形的预测并与多种算法预测结果比较，其中NGO算法的优化效果最佳。Dehghani等[12]提出了NGO算法，并与PSO、GA、GSA、TLBO、GWO、WOA、MPA、TSA等8种算法进行优化性能比较，NGO算法相较于8种竞争算法具有明显的优越性。

鉴于NGO算法强大的优化能力，本文构建了EEMD-NGO-LSTM神经网络耦合模型，通过模仿北方苍鹰的捕猎行为，在搜索空间中寻找LSTM神经网络的最优参数，再对集成经验模态分解后的各个固态模函数进行训练，提高算法全局最优解的搜索能力，进一步提高了径流预测的精度，并用此模型对未来气候变化情景下2030年的年径流进行了预测。

1 研究区域与数据来源

1.1 研究区域

东辽河流域位于东经123°39′～125°32′、北纬42°37′～44°09′之间，流域气候主要为半湿润中温带大陆性季风气候，多年平均气温为5.2 ℃。区域降雨年内分配极不均匀，东部多于西部，多年平均降雨量为661.6 mm。蒸发量为1 020 mm，大体上下游蒸发多于上游。东辽河是辽河东侧的一大支流，发源于东辽县小葱顶子山，流经双辽、辽源、梨树、公主岭等地，境内河长280 km，总河长为448 km，集水面积为9 884 km2。东辽河上游方向有一座大型水库二龙山水库，于1943年建立，总库容为17.6亿m3。在东辽河下游设有王奔水文站，位于东经123°43′北纬43°25′，是东辽河中下游总控制站，集水面积10 418 km2，其中二龙山水库至王奔水文站区间面积为6 489 km2。上游189 km由二龙山水库控制，库区洪水主要由下游降水组成，涨落缓慢，流量较大时水位流量关系呈绳套曲线，含沙量较大，洪峰沙峰相应。王奔水文站的位置见图1。

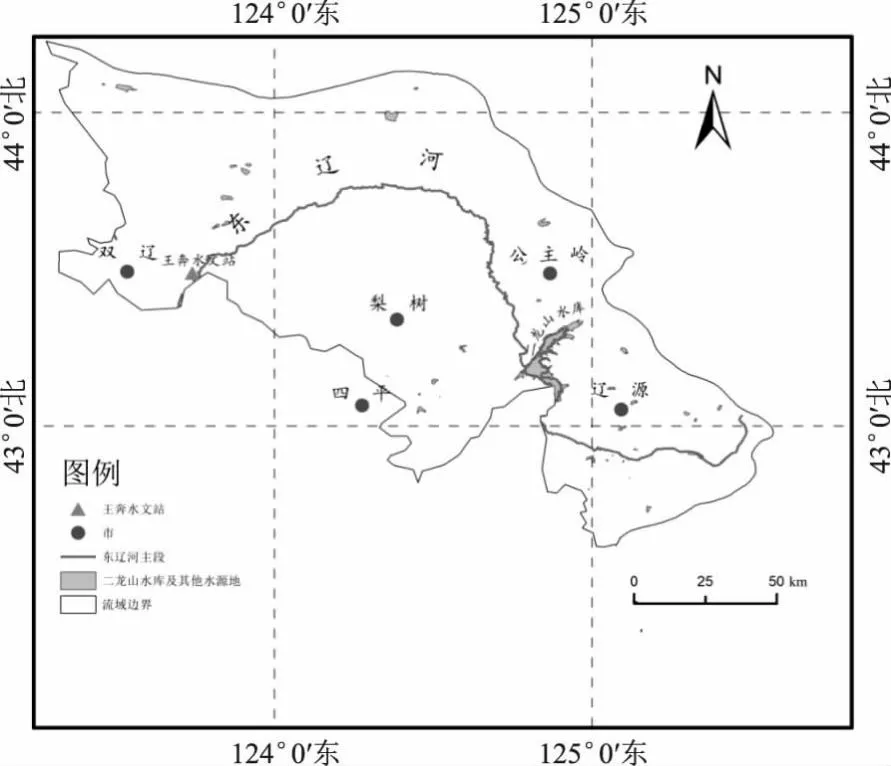
图1 研究区概况

1.2 数据来源

本文所使用的数据来自国家气象科学数据中心(东辽气象局)和王奔水文站，如表1所示。数据主要包括月尺度的径流、降水、蒸发水文气象资料，选取了2012年～2021年共10 a的数据。在数据收集期间研究区域未曾兴建过大型水利工程，下垫面保存较好，流域内的产汇流过程受人类活动影响较小，资料较为可靠，可以真实的反映自然状态下王奔水文站控制流域的径流特征。

表1 2012年～2021年气象和水文数据获取

2 研究方法

2.1 集成经验模态分解(EEMD)

经验模态分解(EMD)的原理是将输入原始信号进行重复筛选、分解，形成一定时间尺度下的IMF分量，再通过 Hilbert变换，将IMF分量的瞬时频率转化为具有物理意义的分量，最终得到非线性、非稳定的原始信号的局部时频特征分布信息[13]。但分解得到的IMF序列可能会出现模态混叠现象，所以在EMD方法的基础上，采用EEMD方法将符合正态分布的白噪声逐步加到原始信号的分析中[14]，利用白噪声改变噪声频率，经过平均计算后，噪声就会相互抵消得到集成平均结果。随着集成平均数的增加，集成平均数和原始信号之间的差异也会减少，得到的结果就越好，在一定程度上克服了IMF序列的模态混叠现象。

该方法实现的具体过程如下：

(1)在原始信号x(t)中添加白噪声w(t)，把添加的白噪声次数记为N次。

xi(t)=x(t)+wi(t)，i=1，2，…，N

(1)

(2)将处理后的原始信号采用EMD方法分解得到m个IMF分量和一个趋势项ri(t)。

(2)

(3)重复添加白噪声，将每次得到的IMF分量进行集成平均处理，作为最终的分解结果。

(3)

式中，xi(t)为处理第i次的原始信号，wi(t)为符合高斯正态分布的白噪声信号，N为添加的白噪声个数，Cij(t)为添加的第j个白噪声后的第i个IMF分量。

2.2 北方苍鹰优化算法(NGO)

北方苍鹰属于中大型猛禽，眼神犀利，速度极快往往使猎物猝不及防。北方苍鹰算法是Mohammad Dehghani等于2021年提出的，是一种基于群的算法，模拟了北方苍鹰在捕捉猎物中的行为，包括搜素辨识、抓捕、追逐与猎物逃亡再追逐等。

2.2.1 初始阶段

模拟的第一步将一只苍鹰看作矢量，那么一群苍鹰就构成了算法的种群矩阵。在初始阶段，每个苍鹰都是随机分布在种群矩阵中。

(4)

式中，X为北方苍鹰种群的矩阵；Xi为第i只苍鹰的初始位置；xi，j为第i只苍鹰在第j维度的位置；M和N分别为苍鹰总数和空间的维度。

目标函数向量为

(5)

式中，F(X)为目标函数的列向量；Fi为第i个目标位置所对应的目标函数值。随着迭代次数的增加，目标函数将会优中选优，直到找到最优解。

2.2.2 搜索识别

根据苍鹰视野良好的特点，算法可以从全领域内选取一个目标进行捕捉，识别的公式为

(6)

(7)

(8)

2.2.3 逃脱抓捕

苍鹰的速度极快，可以迅速将逃脱的猎物追回。在算法中具体表示公式为

(9)

(10)

(11)

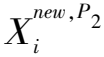
2.3 长短时记忆网络(LSTM)

长短时记忆网络是一种应用广泛的循环神经网络(RNN)的变体，不同于RNN的是它具有类似“门”的结构，LSTM拥有三个门，分别为遗忘门、输入门、输出门，还有一个特殊的记忆细胞。输入门用来控制新信息的量加入到记忆细胞当中，遗忘门决定在时间序列上的信息是否会被遗忘，输出门控制时间序列上信息的输出。通过“门”和“记忆细胞”对数据的准确处理，克服了RNN本身带有的权重影响过大、梯度消失和爆炸的缺点，使神经网络可以更精确、更快速地收敛，能够有效提高预测精度。其基本结构如图2所示。

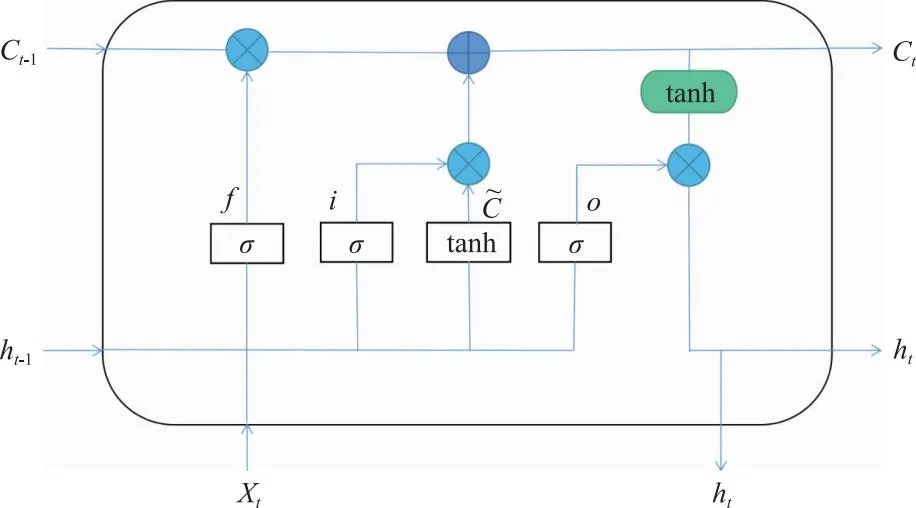
图2 长短期记忆神经网络神经元结构示意

在计算过程中采用的公式为

ft=σ(WfXt+Ufht-1+bf)

(12)

it=σ(WiXt+Uiht-1+bi)

(13)

(14)

(15)

ot=σ(WoXt+Uoht-1+bo)

(16)

ht=tanh(Ct)⊗ot

(17)

2.4 EEMD-NGO-LSTM神经网络耦合模型

EEMD-NGO-LSTM耦合模型的预测径流步骤如下：

(1)对径流数据运用EEMD方法进行分解，得到若干个IMF分量和1个趋势项，并对分解后的结果进行预测。

(2)对苍鹰种群大小、优化参数、适应度函数、迭代次数进行设定，并生成苍鹰个体初始位置。

(3)通过得到的适应度函数计算苍鹰个体的适应度值。

(4)生成苍鹰群矩阵和目标函数向量。

(5)通过公式(6)到公式(11)控制苍鹰移动，进行参数寻优。

(6)开始迭代直到满足最大迭代次数或精度，则将迭代次数带入适应度函数计算适应度值。

(7)得到最佳适应度时苍鹰的坐标，作为LSTM神经网络进行预测时的输入参数，从而对各个分量进行预测。

(8)将各个分量预测的结果进行汇总整合，得到最终的预测结果。

(9)再将调试好的模型中加入CMIP6气候模式下2030年的降水、气温数据，分别对数据进行处理，得到3种气候情景下的2030年径流变化。

3 结果

3.1 EEMD-NGO-LSTM耦合模型的整体性能

对120条月径流数据运用EEMD方法进行分解，分解完毕的径流数据分为5个IMF分量和1个趋势项，分解结果如图3所示。通过经验模态分解，减小了原始数据中的噪声干扰，信号波动趋势趋于稳定，IMF分量逐渐趋于平滑，使预测结果更加准确。将经过EEMD分解后所形成的5个IMF分量的前84项作为训练集，后36项作为测试集，采用NGO-LSTM 模型对测试集分量进行预测。通过预测模型对前84项进行训练，将调优完毕的模型用于后36项的测试，最后对预测结果与实测数据进行比对，EEMD-NGO-LSTM耦合模型的预测结果如图4所示。

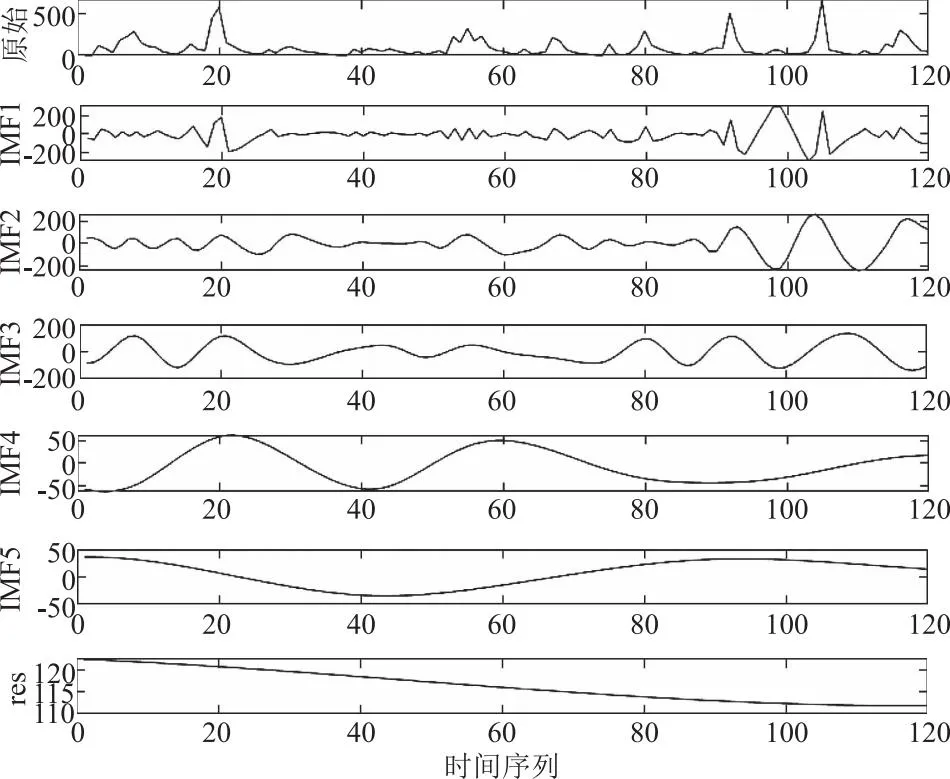
图3 径流数据EEMD分解结果

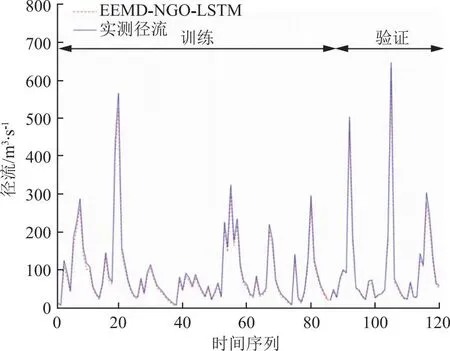
图4 EEMD-NGO-LSTM耦合模型预测结果

为了评估模型预测效果，本文以纳什系数(NSE)、均方根误差(RMSE)、平均绝对误差(MAE)、平均绝对百分比误差(MAPE)和决定系数(R2)作为评价指标。EEMD-NGO-LSTM模型在训练期和验证期间的总体性能统计结果如表2所示。

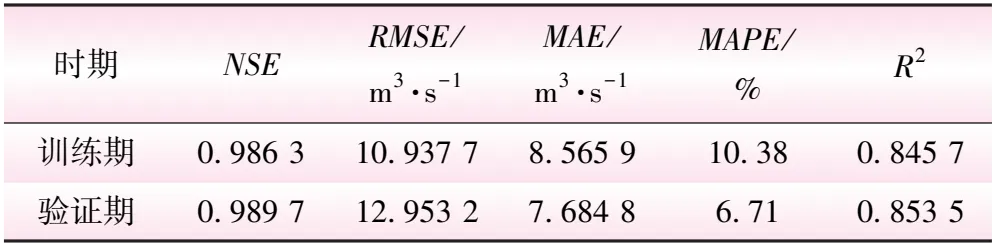
表2 EEMD-NGO-LSTM模型在训练期和验证期间的总体性能统计结果

由表2可知，在训练期和验证期模型的NSE、R2均接近于1，RMSE、MAE、MAPE均较低，说明模型的模拟效果好、质量高、具有较强的可信度，可以用来进行预测。

3.2 模型性能比较

为了验证 EEMD-NGO-LSTM 预测模型的精度，本文还采用WOA-LSTM模型和GWO-LSTM模型来模拟王奔水文站的月径流量，结果如图5、6所示。

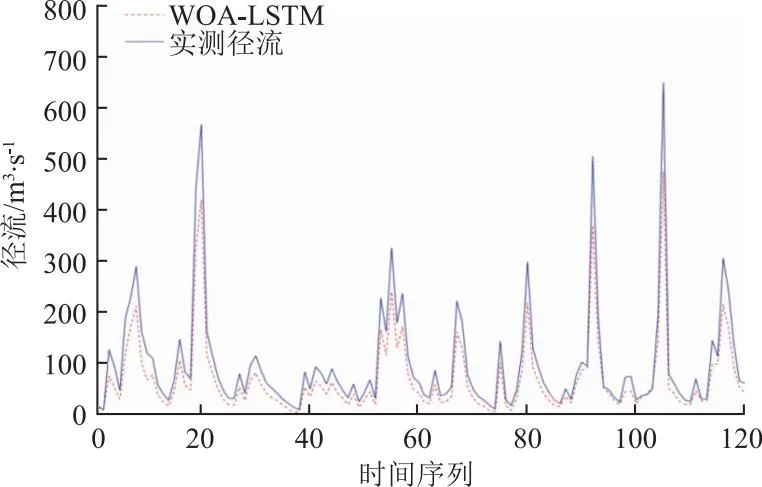
图5 WOA-LSTM模型预测结果

图6 GWO-LSTM模型预测结果

根据以上3种方法预测的结果来看，EEMD-NGO-LSTM耦合模型的模拟情况最佳，且在极值的预测方面也优于其他2种模型；GWO算法预测的效果大部分较好，但有些时间段没有拟合成功，说明灰狼算法在参数优化方面稍逊于EEMD-NGO算法，存在一定的过拟合问题；WOA算法拟合效果较差只能反映一定时间范围内径流的变化趋势，无法对极值进行准确预测。对3种模型的预测精度评价见表3。

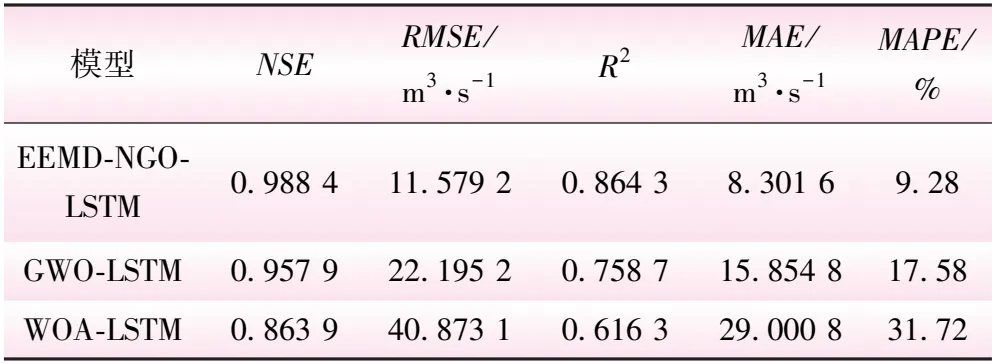
表3 3种模型预测精度评价

由表3可知，EEMD-NGO-LSTM耦合模型的纳什系数(NSE)和决定系数(R2)最接近于1，均方根误差(RMSE)、平均绝对误差(MAE)、平均绝对百分误差(MAPE)均小于其他两种模型，可见EEMD-NGO-LSTM耦合模型总体模拟效果好，精度较高，整体性能最佳。

3.3 王奔水文站月径流量预测分析

王奔水文站的径流量主要受降水和气温影响，随着全球气候变暖加剧，当今气候模型模拟的结果表明，地球表面平均温度每升高1 ℃，大气水汽将增加7%，降水约增加5%。根据CMIP6气候模式下的2030年气温降水数据，本文设置了3种气候预测情景。

3.3.1 假设气温升高1 ℃，降水不变

在此种条件下，2030年王奔水文站的径流量比2012年～2021年的平均径流量增加6.61%(见图7a)，1月～4月径流量减少，这可能由于温度升高，地表开始解冻，在下渗和蒸发双重作用下径流减小；5月～8月径流的增加情况显著，这可能由于气温的升高导致河流中的浮冰融化，水汽运移速度加快；9月～10月径流量呈下降趋势，这可能由于气温升高，蒸发加剧导致的。11月～12月份随着气温降低，河流结冰使径流量减少。

图7 2030年不同气候情景下王奔水文站月平均径流量的变化

3.3.2 假设降水升高5%，气温不变

在此种条件下，2030年王奔水文站的径流量比2012年～2021年的平均径流量增加6.95%(见图7b)。1～3月径流量增加可能原因是由于气温升高加速冰雪消融，使融化的水汇入地表河网使径流增加。4月径流量减小可能原因是气温下降河水结冰，5月～8月是雨季同时伴随气温升高会使土壤表层和深层冰雪进一步融化导致径流增加。9～12月气温下降，降雪量增加冰雪融水逐渐减少，蒸发量和下渗量也相应减少导致径流量减少。

3.3.3 假设气温升高1 ℃，降水升高5%

在此种条件下，2030年王奔水文站的径流量比2012年～2021年的平均径流量增加22.16%(见图7c)，3月～7月径流量有逐渐增加的态势，直到8月份增加到最大值，其余月份忽高忽低。

4 讨论

4.1 径流预测的潜在影响因素

4.1.1 算法迭代速度分析

为了进一步探究径流预测的潜在影响因素，考察算法参数优化速度。将迭代次数设置为120次，种群大小设置为300。不同算法的优化收敛结果如图8所示。WOA和GWO算法的收敛速度低于EEMD-NGO算法。NGO算法在迭代到第17次时率先到最优状态，适应度为0.6。3种模型的具体速度表现见表4，这表明EEMD-NGO的遍历全局以及搜寻目标的能力是优于其他两种算法的。采用此算法加强了LSTM神经网络对径流的预测效果，提高了模型的精度。

表4 3种模型迭代表现

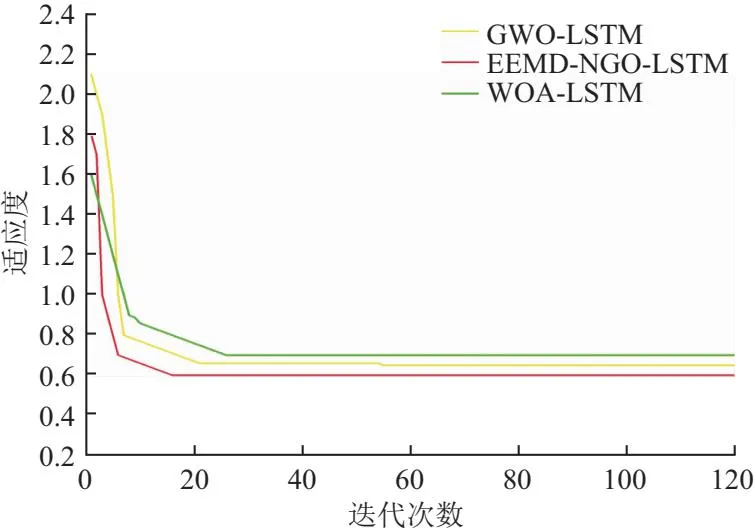
图8 三种优化算法的收敛曲线

4.1.2 模型机理分析

由于本模型是数据驱动的模型，只能反映径流变化的大致规律，做到近似代替，无法从径流形成的机理上说明径流变化的情况。且因算法本身的特点，也无法准确地把径流的变化过程提炼出来，就会造成一定的预测偏差，这些问题可以通过完善算法或者输入大量的数据得到改善。

4.2 径流变化的影响因素

径流的形成主要由降水和气温的变化决定[15]，但气温同时又影响降雨和蒸发[16]。气温的降低导致空气中的水汽冷凝，达到成水的温度时开始降雨，温度升高又会导致水面蒸发进而影响径流。刘美玲等[17]通过气象因子间的灰色关联分析，得出在齐齐哈尔地区的蒸发与气温和降水的相关性最为密切，与平均风速关联度最低。赵美亮等[18]采用趋势分析和数理统计方法得出大通河的径流量与降水和平均气温呈正相关。综上所述，在预测模型中添加降水、气温要素可以更加细致的模拟径流过程，达到提高预测精度的目的。