岩土复合地层双孔隧道开挖对地表沉降的影响

黄 戡，黄先强，杨海涛

(1.长沙理工大学土木工程学院，湖南长沙410114；2.深圳大学土木与交通工程学院，广东深圳518061)

0 引 言

在城市修建双线隧道常常穿越上软下硬复合地层，双线隧道施工容易引起上部软土层发生不均匀沉降，甚至诱发地表发生塌陷，给邻近建筑物造成巨大危害。目前，国内外学者研究复合地层双孔隧道开挖引起地表沉降的问题主要采用的方法有经验公式法[1-2]、数值分析法[3-4]以及理论解析法。理论解析法是基于严密的数学推导得到的计算公式，是预测双孔隧道开挖引起地表沉降的一种有效方法，其中最常用的是随机介质法和复变函数法。波兰学者Litwinszyn[5]建立了随机介质理论，随后经过我国学者刘宝琛等[6]的发展，随机介质理论被广泛应用到城市地铁隧道施工引起的地表变形预测中。魏纲等[7-8]针对后行隧道施工引起的不对称地表沉降，通过引入轴线偏移量对随机介质理论进行修正，获得适用于预测平行双线隧道的计算方法。然而上述研究均是将岩土层视为一种介质，李涛等[9]将土层和岩层看作2种不同的介质，采用随机介质理论得到了岩土复合地层单线隧道开挖引起的地表变形计算公式，但是在计算过程中忽略了上部软土层自重的影响，这也与实际并不吻合。

为求解双洞开挖对地层的影响，晏莉等[10]采用复变函数法和Schwarz交替法得到平行双孔隧道开挖对土体应力和位移的半解析解。张治国等[11]采用复变函数和Schwarz交替法研究了不同布置方式下浅埋双孔隧道开挖对地层变形的影响。以上学者求解双孔洞问题时，将隧道岩层和上覆软土层视为均匀单一的地层，然而在实际工程中，地层一般成层分布，岩层与土层的物理力学性质存在较大差异，忽略该差异性将会导致理论计算结果产生较大误差。

针对岩土复合地层双孔隧道开挖的理论研究相对较少，本文提出复变函数理论和随机介质理论相结合的计算方法，分析岩土复合地层双孔平行隧道开挖对岩土体沉降的影响，研究不同隧道半径、隧道间距以及土层主要影响角对地表沉降的影响。

1 问题描述

为简化计算，根据复变函数和随机介质理论的特点以及局限性作出以下基本假定：①根据隧道的形状和受力特点，该问题满足平面应变问题的条件；②岩体为各向同性的均质线弹性体，土体为均质散体材料；③将作用于岩土分界面的上覆土层自重荷载视为均布荷载；④岩土分界面沉降和隧道洞周变形为小变形，迭代过程中映射函数的表达式保持不变。

建立半无限平面复合地层双孔平行隧道开挖问题的计算模型，见图1。图1中，隧道中心到岩土分界面的距离为h；岩土分界面到地表的距离为H；2条隧道之间的间距为d；隧道半径为r；E1、E2分别为土层和岩层的弹性模量；μ1、μ2分别为土层和岩层的泊松比；γ1、γ2分别为土层和岩层的容重；R区域为岩层中隧道开挖面外的区域；Q区域为土层区域。取隧道1和隧道2的局部坐标系分别为x1o1y1、x2o2y2，地表的坐标系为x3o3y3。

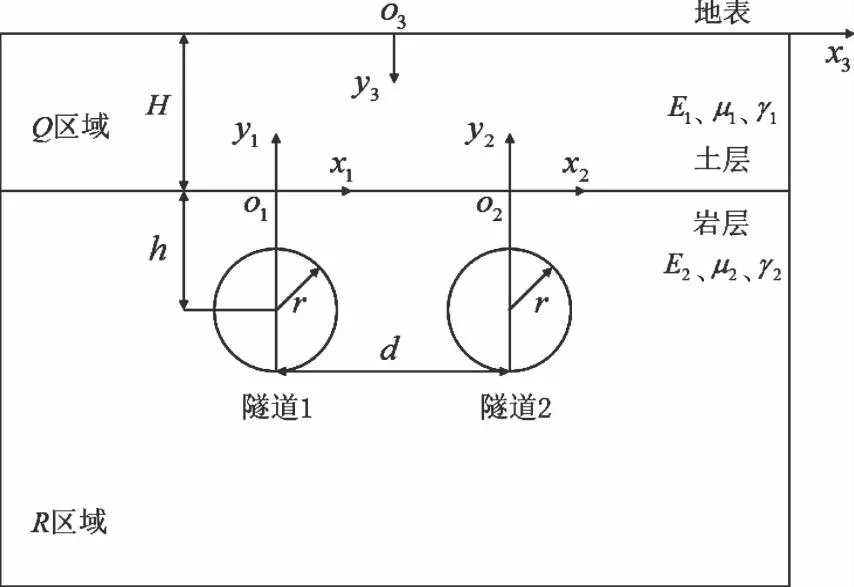
图1 复合地层双孔隧道开挖模型

2 岩层双孔隧道开挖问题求解

2.1 岩土分界面沉降求解

计算过程中，需要将土层与岩层分开计算，将岩层双孔隧道开挖问题视为半无限平面双孔洞问题，将上覆土层的自重应力均匀等效地作用在岩土层分界面，计算模型见图2。图2中，竖向荷载qy=-γ1H；水平荷载qx=-k0γ1H；k0为侧压力系数，将其视为分界面的应力边界条件[12]。

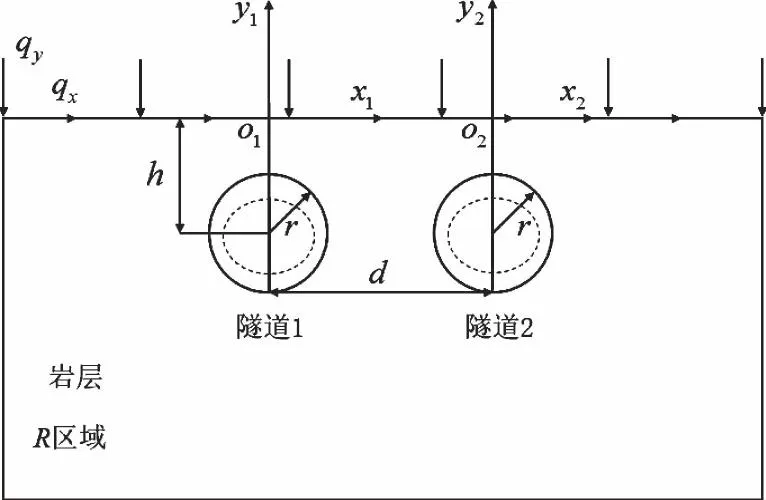
图2 岩层双孔隧道开挖模型

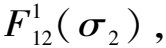
(2)将上述求得的附加面力作为隧道2的初始应力边界条件，并利用复变函数理论得到解析函数φ21(ζ2)和ψ21(ζ2)，此时第1次迭代结束，隧道2周边满足0应力边界条件。

(3)同样利用Schwarz交替法通过隧道2的解析函数φ21(ζ2)和ψ21(ζ2)获得隧道1的附加面力，并利用傅里叶级数逼近，最后利用复变函数理论求解得到第2次迭代隧道1的解析函数φ12(ζ1)和ψ12(ζ1)，并求得隧道2的附加面力。

(4)重复上述步骤(2)～(3)，经过多次迭代之后，洞周的附加面力已经足够小，可以认为满足工程需求，停止迭代计算。

(5)对隧道2的求解采用与步骤(1)～(4)相同的方法，当隧道2求解完毕后，将上述所有的解析函数叠加为φ(ζ)和ψ(ζ)，将其代入下式即可得到岩土分界面的沉降[15]，即

(1)

式中，u和v分别代表岩层的水平位移和竖向位移；i为虚数单位；G为岩体剪切模量；κ为围岩力学参数，考虑平面应变问题，取κ=3-4μ2；ω(ζ)为映射函数。

2.2 地表沉降求解

根据随机介质理论，单元开挖示意见图3。图3中，在求解地表沉降时，地层采用整体坐标系x3o3y3，开挖变形部分采用局部坐标系ε、η。其中，ε、η分别为开挖变形部分到y轴和x轴的距离，取无限小开挖单元dεdη，由开挖单元dεdη引起的距离单元中心为x的地表沉降为We(x)，计算公式如下[6]

(2)

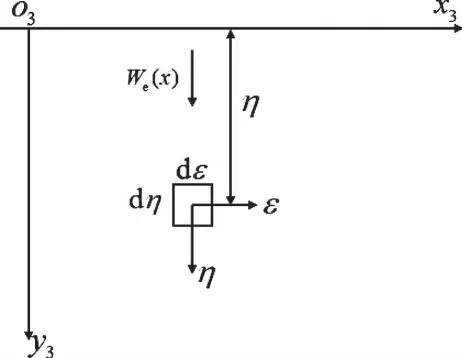
图3 单元开挖示意

式中，β为地层的主要影响角。

将双孔隧道开挖引起岩土分界面的沉降曲线与分界面所围成的区域记作M，复合地层沉降传递示意见图4。图4中，a1、b1、c1、d1为双重积分的上下限，A、B、C为抛物线系数，利用抛物线y=Ax2+Bx+C拟合分界面沉降曲线[9]，确定a1、b1、c1、d1。

图4 复合地层沉降传递示意

假定在“不等厚开挖”区域M内的开挖单元均发生变形，通过积分得到地表沉降计算式，即

(3)

根据土层的内摩擦角φ确定土层的主要影响角，通常经验公式[16]求出土层的主要影响角β，即

(4)

双孔隧道埋深、间距会影响岩土分界面的沉降曲线形态。当间距较大时，沉降曲线呈“W”形分布，此时需要先计算得到隧道1开挖及作用在其洞周的附加面力所引起的分界面沉降曲线，再计算该部分的地表沉降；然后针对隧道2开挖及作用在其洞周的附加面力所引起的分界面沉降曲线，采用相同的方式计算该部分的地表沉降；最后将2个部分的地表沉降进行线性叠加，即可得到地表沉降的最终值。复合地层沉降传递见图5。

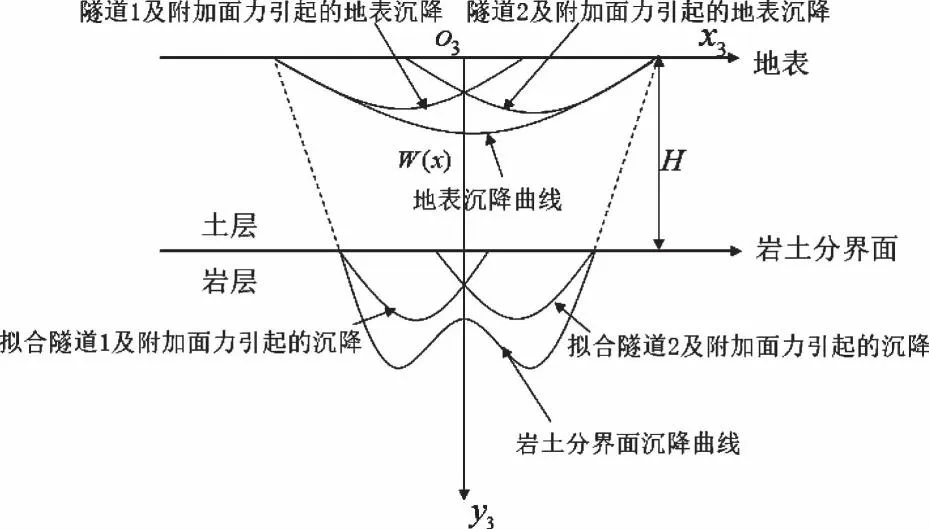
图5 复合地层沉降传递

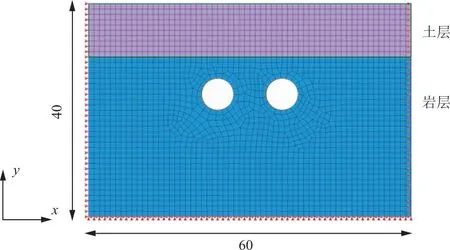
图6 复合地层双孔隧道有限元模型(单位：m)

3 与有限元结果对比

由于利用复变函数理论和随机介质理论联合求解复合地层双孔隧道开挖问题仍处于发展阶段，为了验证本文计算方法的可靠性，拟采用有限元软件MIDAS GTS NX建立平面应变模型与理论计算结果进行对比。有限元模型水平和竖向分别为60 m和40 m，对模型底部进行固定位移约束，左右两侧进行水平约束，土层采用M-C本构模型，土层厚度为10 m，容重为18.5 kN/m3，黏聚力为19 kPa，内摩擦角为17°，弹性模量为20 MPa，泊松比为0.3；岩层采用线弹性本构模型，岩层容重为21 kN/m3，弹性模量为100 MPa，泊松比为0.28；隧道半径为3 m，隧道中心埋深17 m，2条隧道中心的间距为12 m。

利用本文所提出的计算方法计算岩土分界面以及地表沉降，将计算结果与有限元结果和不考虑岩土分层的计算结果进行对比，在不分层计算过程中，直接将岩土体的物理力学参数进行加权平均，最后得到不同计算方法的分界面沉降曲线和地表沉降曲线，结果见图7。

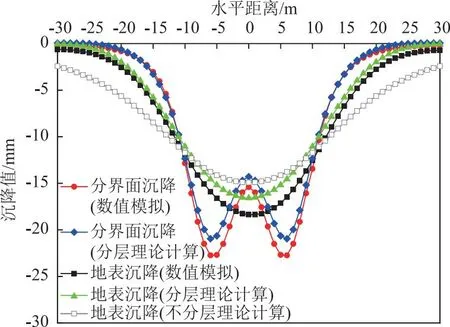
图7 地层沉降曲线对比

从图7可知，对于岩土分界面上的沉降曲线，数值模拟结果和本文分层理论计算的沉降曲线较为吻合，沉降曲线形态均为“W”形，最大沉降值出现在左右两侧隧道中心的正上方，数值模拟得到的最大沉降值为22.739 mm；而采用本文理论计算方法得到的最大沉降值为20.95 mm，计算相对误差为7.9%。对于地表的沉降曲线，相较于不分层的理论计算沉降曲线，分层的理论计算沉降曲线与数值模拟结果更加吻合，数值模拟得到的最大沉降值为18.369 mm，分层的理论计算最大沉降值为16.579 mm，相对误差为9.7%，而不考虑分层时的理论计算最大沉降值为14.919 mm，相对误差为18.8%。因此，在计算岩土复合地层双孔隧道开挖引起的地表沉降时进行分层计算是十分必要的。

4 地表沉降影响参数分析

选取不同隧道开挖半径、隧道间距以及土层主要影响角，对岩土复合地层双孔平行隧道开挖引起的地表沉降规律进行研究分析。具体参数取值如下：隧道半径r=3 m，隧道中心距分界面距离h=8 m，隧道间距d=12 m，土层厚度H=10 m，tanβ=0.5。在研究其中1个参数的影响时，保持其他参数不变。

4.1 隧道开挖半径

为分析不同隧道开挖半径下的岩土复合地层双孔隧道开挖对分界面沉降及地表沉降的影响，考虑隧道半径r分别取为2、2.5、3 m和3.5 m这 4种不同工况计算，计算结果见图8。

图8 不同隧道半径对地层沉降的影响

从图8可知，分界面的沉降曲线均为“W”形或浅“W”形，呈现出“双峰”形态，最大沉降值位于左右隧道中心的正上方处；地表沉降曲线为“U”形或“V”形，呈现为“单峰”形态，地表最大沉降值位于2个隧道的中心处，这是受隧道间距以及隧道埋深的影响。随着隧道开挖半径的增大，分界面沉降和地表沉降值均逐渐增大，这是因为隧道开挖半径越大，对洞周的岩土体产生的扰动越大。

4.2 隧道间距

由于双孔隧道的间距对土层变形的影响很大，为分析不同隧道间距下的岩土复合地层双孔隧道开挖对分界面沉降及地表沉降的影响，考虑隧道间距d分别取为8、12、16 m和20 m这4种不同工况计算，计算结果见图9。

图9 不同隧道间距对地层沉降的影响

从图9可知，随着隧道间距的增加，分界面沉降曲线形态由“U”形向浅“W”形再向“W”形逐渐变化，且最大沉降值随之减小，最大沉降值的位置逐渐远离2个隧道的中心；地表沉降曲线形态也是由“V”形向“U”形再向浅“W”形逐渐演变，地表最大沉降值逐渐减小。当间距为8 m时，地表最大沉降值为16.149 mm，而当间距为20 m时，地表最大沉降值为9.93 mm，且最大沉降值位置为左右2个侧隧道的中心正上方处。由此可见，隧道间距对地表沉降的影响不可忽视，因此在实际工程中应该将隧道间距作为重要考虑因素。

4.3 土层主要影响角

为分析不同土层主要影响角下的岩土复合地层双孔隧道开挖对地表沉降的影响，考虑tanβ分别取为0.4、0.5、0.7和0.9这4种不同的工况计算，计算结果见图10。

从图10可知，地表最大沉降值位于2个隧道中心处，且随着tanβ的增大，地表最大沉降值随之逐渐增大，但是增大的幅度逐渐减小。tanβ从0.4增加到0.5时，地表最大沉降值增大了1.56 mm；而tanβ从0.7增加到0.9时，地表最大沉降值仅仅增大了0.28 mm；随着tanβ的增大，地表沉降的影响范围不断减小，即地表沉降槽宽度逐渐减小。

5 结 语

本文基于理论分析和数值计算，采用复变函数理论和随机介质理论结合的计算方法，求解岩土复合地层双孔平行隧道开挖问题，对岩土复合地层双孔隧道开挖对地层沉降的影响进行了研究，得出以下结论：

(1)先利用复变函数法和Schwarz交替法获得分界面处的沉降，然后将分界面处的沉降视为“不等厚开挖”，通过随机介质理论计算出地表沉降，该计算方法能够充分考虑岩土体2种材料物理力学性质的差异。

(2)利用本文所提出的分层理论方法计算岩土分界面以及地表沉降，并将计算结果与有限元结果和不考虑岩土分层的计算结果进行对比可知，考虑岩土分层的计算结果与有限元结果更加吻合。

(3)随着隧道开挖半径的增大，地表沉降逐渐增大；随着隧道间距的增大，地表沉降曲线形态由“V”形向“U”形再向浅“W”形逐渐演变，地表最大沉降值随之减小；随着土层主要影响角的增大，地表最大沉降值逐渐增大，地表沉降槽宽度逐渐减小。