基于不同河道汇流方法的新安江模型研究

王 也，龚 定，李致家，肖 杨，谭 君，李巧玲

(1.五凌电力有限公司，湖南长沙410004；2.安徽省水利水电勘测设计研究总院有限公司，安徽合肥230088；3.河海大学水文水资源学院，江苏南京210024)

0 引 言

河道汇流演算在流域洪水预报中起着关键性的作用。我国幅员辽阔，流域特点各不相同，汇流条件复杂[1]。在汇流过程中，河道内水流运动受地形影响较大[2-3]，对不同特性的流域选择合适的汇流方法进行洪水预报，有利于实现更高精度的实时洪水预报。

五强溪水库作为沅水流域下游控制性水库，对沅水流域的防洪调度有显著的影响，是国家防洪重点水库之一。五强溪水库入库洪水的预报精度直接影响水库调度决策及下游洞庭湖等地区的防汛安全。为了针对五强溪流域建库后河道天然条件改变的情况，本文在河道汇流方面从水文学和水力学角度出发，加入局地惯性波法，提出组合河道汇流方案，以期更贴近真实地模拟河道情况，从而提高洪水预报精度，为五强溪水库配置水资源、防汛抗旱、应对洪涝灾害风险等提供决策依据具有重要的意义。

1 流域概况

五强溪流域属于亚热带季风气候，降水时间分布不均，暴雨发生较为频繁且集中在年内4月～9月，年降水量在1 500 mm左右。1996年12月，五强溪水电站5台机组全部投产发电，装机容量达到了120万kW，五强溪流域正式建库完成。建库后，形成了以五强溪站为出口的五强溪流域。五强溪水库坝址以上流域集水面积超过8万km2，属于季调节水库，调节库容较小，对沅水流域的防洪调度起着关键性的作用。为了更准确地预报五强溪流域流量过程，统计多场洪水的暴雨中心，研究流域面积为8 033 km2，划分10个子流域，五强溪流域示意图见图1。流域上游共有浦市、河溪和高砌头3个入流站，主要以浦市来水为主。区间洪水具有流程较短、汇流速度快、突发性强的特性，近坝区暴雨洪水时常与3个上游控制站以上流域来水相叠加，使得库区水位迅速抬升[4]，从而使得水库洪水预报与调度的时间短，增加了实时预报准确性的难度。五强溪流域属于湿润地区，下垫面条件和径流关系较好，选用新安江模型对流域内洪水进行预报。本文收集整理了2020年～2022年4个控制站(浦市、河溪、高砌头、五强溪坝上)的逐日流量过程，以及近坝区28个观测资料较为齐全雨量站的逐日降雨资料，从中选取了10场包括大、中、小不同量级的洪水进行五强溪水库近坝区洪水预报方法改进研究。

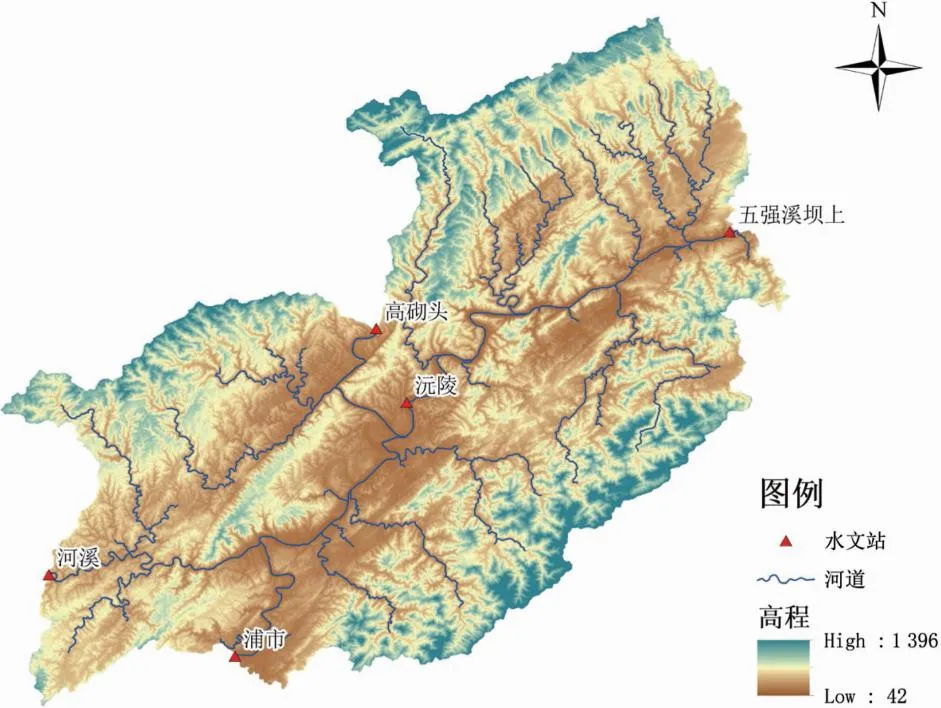
图1 研究流域及河道示意

2 研究方法

2.1 新安江模型

新安江模型属于概念性水文模型，在实际应用中通常把流域分成多块，目前新安江模型流域的划分主要是利用GIS技术，根据流域的DEM数据进行自动的流域划分，并提取相应的地理学参数，对每块子流域进行产汇流计算，汇总得到研究流域的径流过程[5]。新安江模型4个模块分别为：蒸散发模块、产流模块、分水源模块和汇流模块。每个模块的流程见图2。

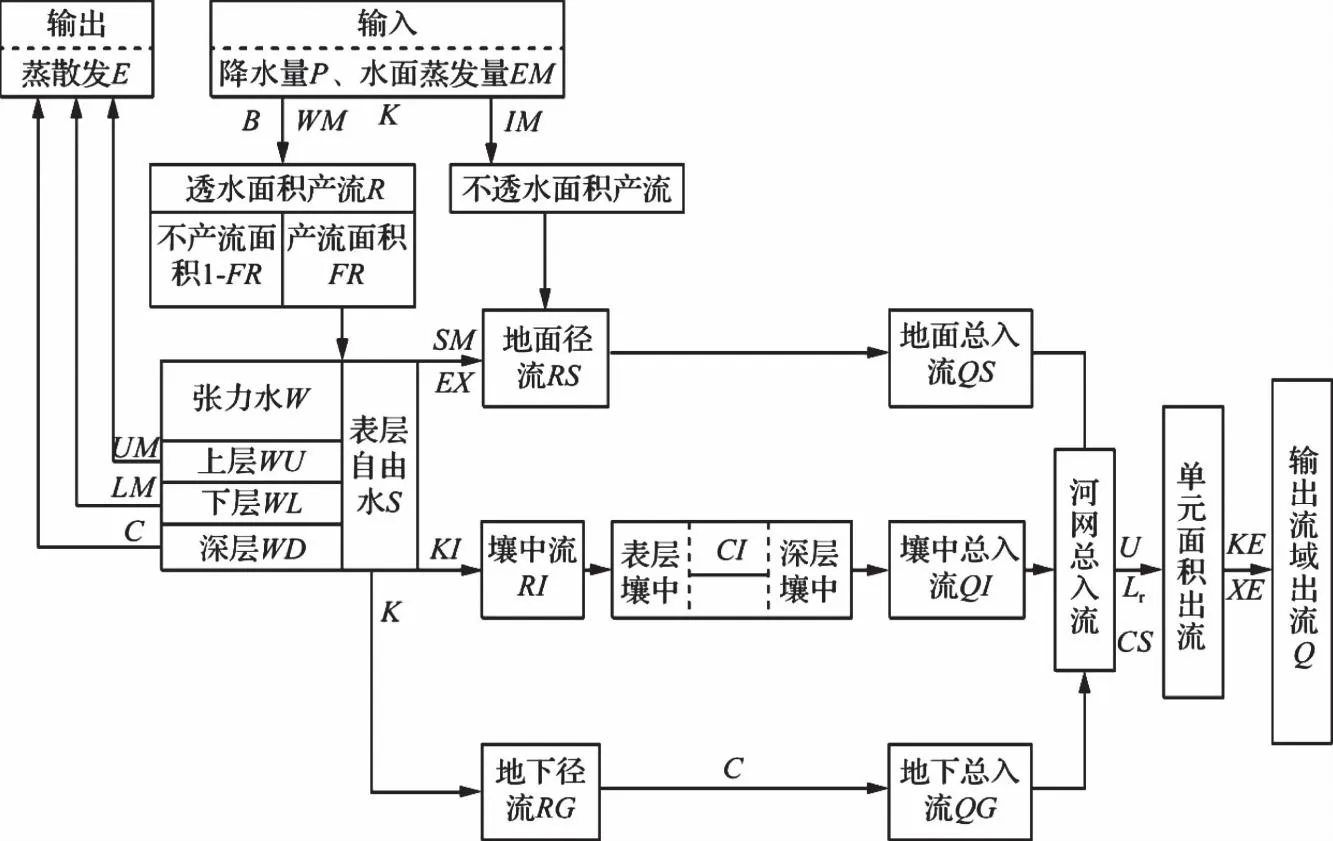
图2 新安江模型结构概化

2.2 分段马斯京根法

传统的马斯京根法基于水量平衡方程和槽蓄方程[6]，联立成为马斯京根法的公式组

(1)

式中，O2、O1分别为下一个时段和当前时段河段下断面的出流量，m3/s；I1、I2分别为当前时段和下一个时段河段上断面的入流量，m3/s；C0、C1、C2均为演算系数；Δt为计算时段步长，h；k为槽蓄系数；xk为流量比重系数。

对于具体的研究河段，参数k和xk根据历史洪水资料，利用试算法，假定xk值，绘制槽蓄曲线，从而进行率定xk值并得到k值。但在真实河道中，由于长河道水流会带来水流不稳定问题，很难满足假定的河段入流量和出流量在时段Δt内是线性变化的、流量在河段内的沿程变化是线性的两个线性条件，且k值大于Δt。为了提高方法适用性，需要采用分段马斯京根法，把长河段分成若干短河段进行连续演算[7]，分段马斯京根法参数ke、xe可由k、xk计算，公式为

(2)

(3)

式中，ke为分段的槽蓄系数；xe为分段流量比重系数；N为河道分段数。

2.3 局地惯性波法

描述缓变不稳定流的数学方程是由St. Vennat于1871年导出[8]的，由连续性方程和动力方程构成。无旁侧入流情况下，缓变不稳定流的连续性方程为

(4)

式中，Q为流量，m3/s；A为过水断面面积，m2；x为沿水流方向的步长，m；t为时间，s。

无旁侧入流情况下，缓变不稳定流的动力方程为

(5)

式中，h为水深，m；z为河底高程，m；n为河道糙率；R为水力半径，m；g为重力加速度，一般取值为9.8 m/s2。

运动波忽略了惯性项和附加比降项，适用于山区性河流；扩散波忽略了惯性项，适用于河底比降平缓的河流中、下游段[9]。但当河底比降进一步减小，惯性项不可忽略时，如底坡较缓河道和水库型河道，考虑惯性项的惯性波可以很好地对此类河道进行流量演算。

2007年Hunter等人提出对于许多洪泛平原，迁移加速项相对不重要[10]。传统的惯性波中重力项和阻力项恰好相抵消，即忽略这两项。本文提出局地惯性波，保留重力项，阻力项和局地惯性项，忽略迁移加速项。同时假设一个矩形河道，得到方程式

(6)

根据时间步长Δt离散方程式，整理排列得到流量Q在时间t+Δt的显式方程，得到局地惯性波的演算公式[11-12]

(7)

2.4 汇流方法配置

局地惯性波适用于河底较为平缓的河流或靠近库区的回水区河道，五强溪水电站建成开始蓄水后，改变了原有河道的天然状况，在靠近库区的河道水面比降减小，库区河段水深增加，附加比降增大，考虑在回水区使用局地惯性波，回水区以外使用分段马斯京根法。水库型河道在靠近库区时一般为变动回水区，变动回水区是指靠近水库上游一段河道内可能会因为回水影响分别表现出水库特性和河道特性的河段，是库区到天然河道的过渡段，其长度定义为不同库区水位下回水曲线末端的移动范围[13]，示意图见图3。

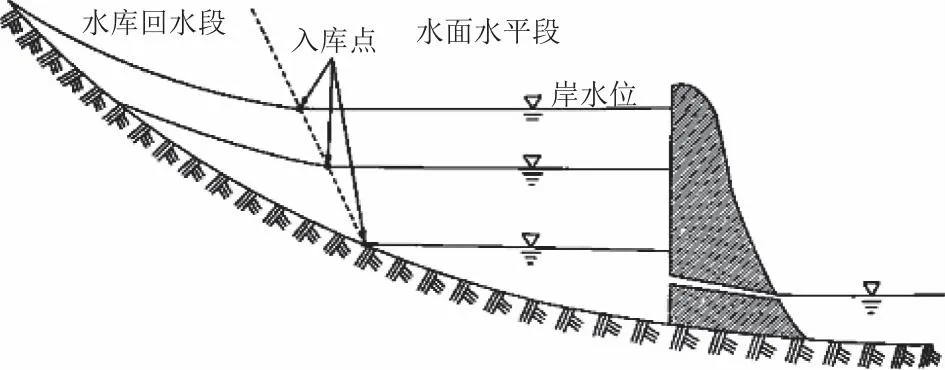
图3 水库回水段示意

根据库区水位资料，进行回水区范围确定，回水区范围见图4。沅陵在回水段附近，库区水位站只有沅陵站，考虑以沅陵站为界结合使用2种汇流演算方法，即沅陵站以上使用分段马斯京根法，沅陵站属于水位站，没有实测流量资料，所以分别将3个上游站入流演算至沅陵站，获得总流量数据；沅陵站以下至入库点，即变动回水区段，使用局地惯性波法进行演算。具体汇流模块配置方案见表1。

表1 河道汇流模块配置方案情况

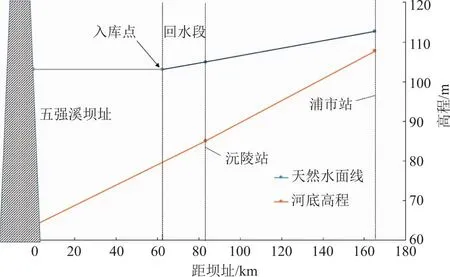
图4 五强溪流域主河道概化

2.5 参数率定

2.5.1 新安江模型参数

基于2020年～2022年五强溪近坝区所有水文站和雨量站及浦市、河溪、高砌头和五强溪坝上的日流量和雨量资料及相应的时段资料，采用蒙特卡罗随机采样模型自动优选和人工调试相结合的方法，率定新安江日模型和次洪模型参数，率定的日模和次洪参数见表2。

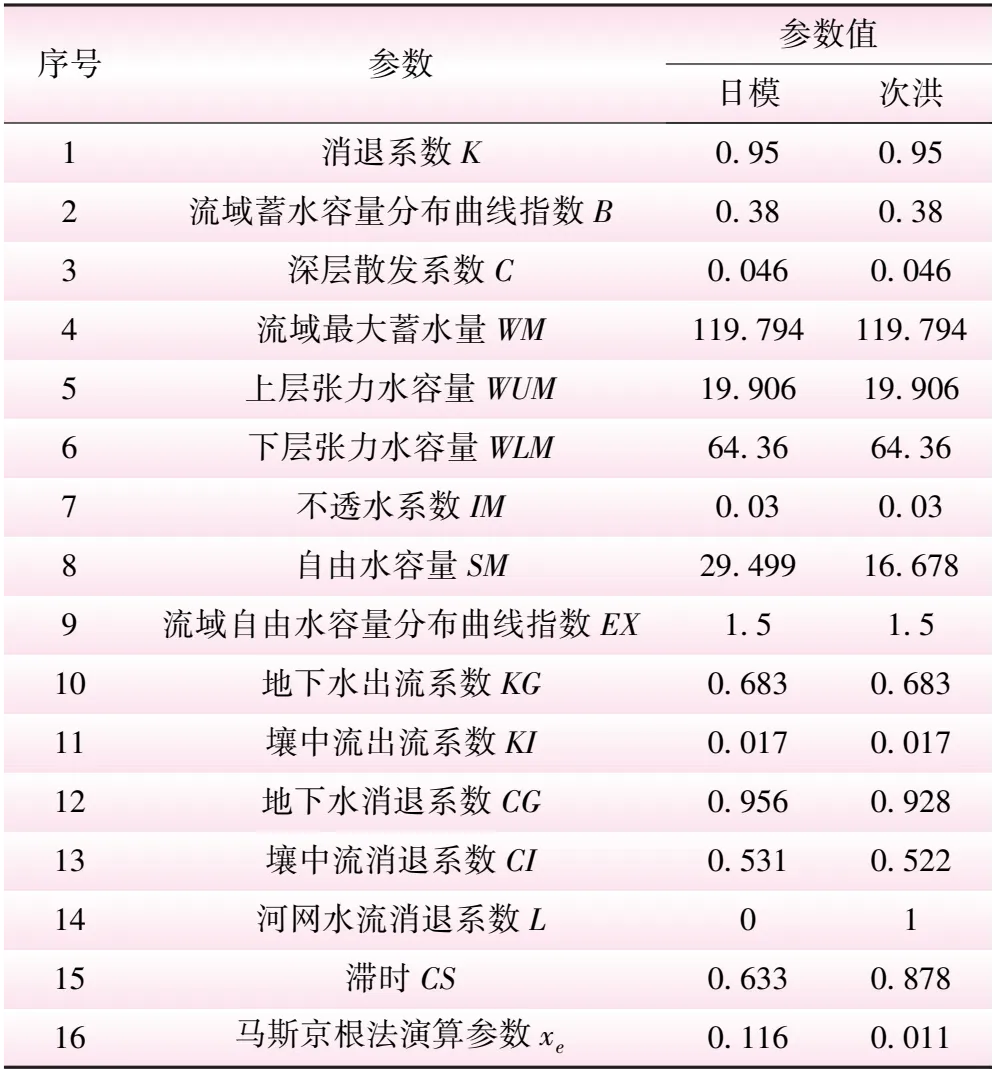
表2 五强溪流域新安江模型参数

2.5.2 方案1参数

根据实测流量资料率定分段马斯京根法3个入流站参数，分段数一般表现为洪水在站点之间的传播时间，即洪水的预见期。距离越远，一般汇流时间越长，段数越多。具体数据见表3。

表3 分段马斯京根法参数

2.5.3 方案2参数

方案2为两段式汇流结构。第一段采用分段马斯京根法从流域3个入流站演算至沅陵，根据实际汇流时间确定分段数，流量比重系数不变。参数见表4。

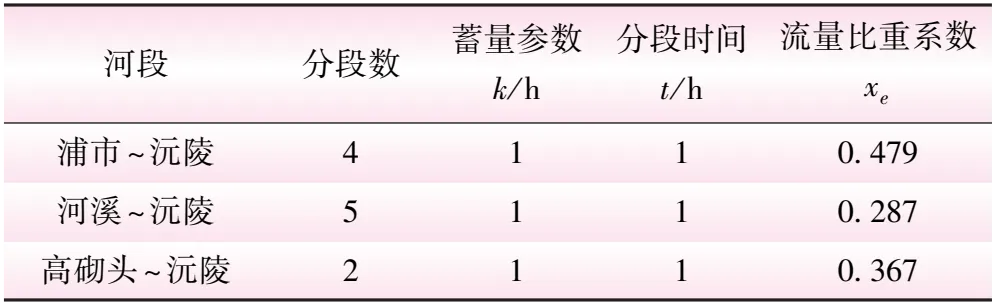
表4 入流—沅陵站分段马斯京根法参数

第二段为水库回水区，由沅陵站局地惯性波法演算至入库点。根据典型场次洪水，确定入库代表点，沅陵站水位与库区水位较为接近，且沅陵站为靠近库区的唯一有水位数据站点，以沅陵站为回水区末端。由图4可知，入库点距沅陵约83.1 km，距回水段约20.8 km，根据河道情况确定局地惯性波法参数，参数见表5。

表5 回水段局地惯性波法参数

2.6 精度评价指标

根据GB/T 22482—2008《水文情报预报规范》的建议，考虑选用确定性系数DC、洪峰相对误差RPE、峰现时间误差TE、洪量相对误差RRE作为模拟精度评价指标。

2.6.1 确定性系数DC

确定性系数DC用于描述洪水模拟过程与实测过程之间的契合程度，当模拟序列与实测序列完全重合时，模型模拟结果为最优拟合，DC值为1。DC指标的计算公式为

(8)

DC值越接近1，表明模拟过程越接近实测过程；反之，则表明模拟过程越偏离实测序列。DC的合格线值为0.6。

2.6.2RPE指标

RPE指标计算公式为

RPE=(qc，p-qo，p)/qo，p×100%

(9)

式中，qc，p为模拟洪峰值；qo，p为实测洪峰值。

RPE指标表示洪峰流量模拟的误差大小，其绝对值越大，表明模拟洪峰与实测洪峰的差距越大。RPE为负值说明模拟洪峰偏小，反之偏大。实测洪峰流量的合格误差在±20%以内。

2.6.3TE指标

TE指标计算公式为

TE=tc，p-to，p

(10)

式中，tc，p为模拟洪峰出现的时刻；to，p为实测洪峰出现的时刻。

TE用于描述模拟序列与实测序列洪峰出现时间的差距，TE为负值时，说明模拟洪峰出现时间较早，反之滞后。以模拟开始时间实测峰现时间时距的30%，为允许偏差，如果允许偏差低于±3 h，那么允许偏差为±3 h，作为峰现时间是否合格的判断标准。

2.6.4RRE指标

RRE指标计算公式为

RRE=(Rc-Ro)/Ro×100%

(11)

式中，Rc为模拟洪量值；Ro为实测洪量值。

RRE用于描述单场洪水过程计算洪量与实测洪量之间的偏离程度；洪量的合格误差在±20%以内。

3 结果分析

将新安江模型分别配置以上2种汇流方案进行建库后五强溪流域场次洪水模拟，比较2种方法构成的河道汇流方案的洪水模拟结果，模拟过程如图5所示，分析讨论不同河道汇流演算方法在新安江水文模型中的应用效果。

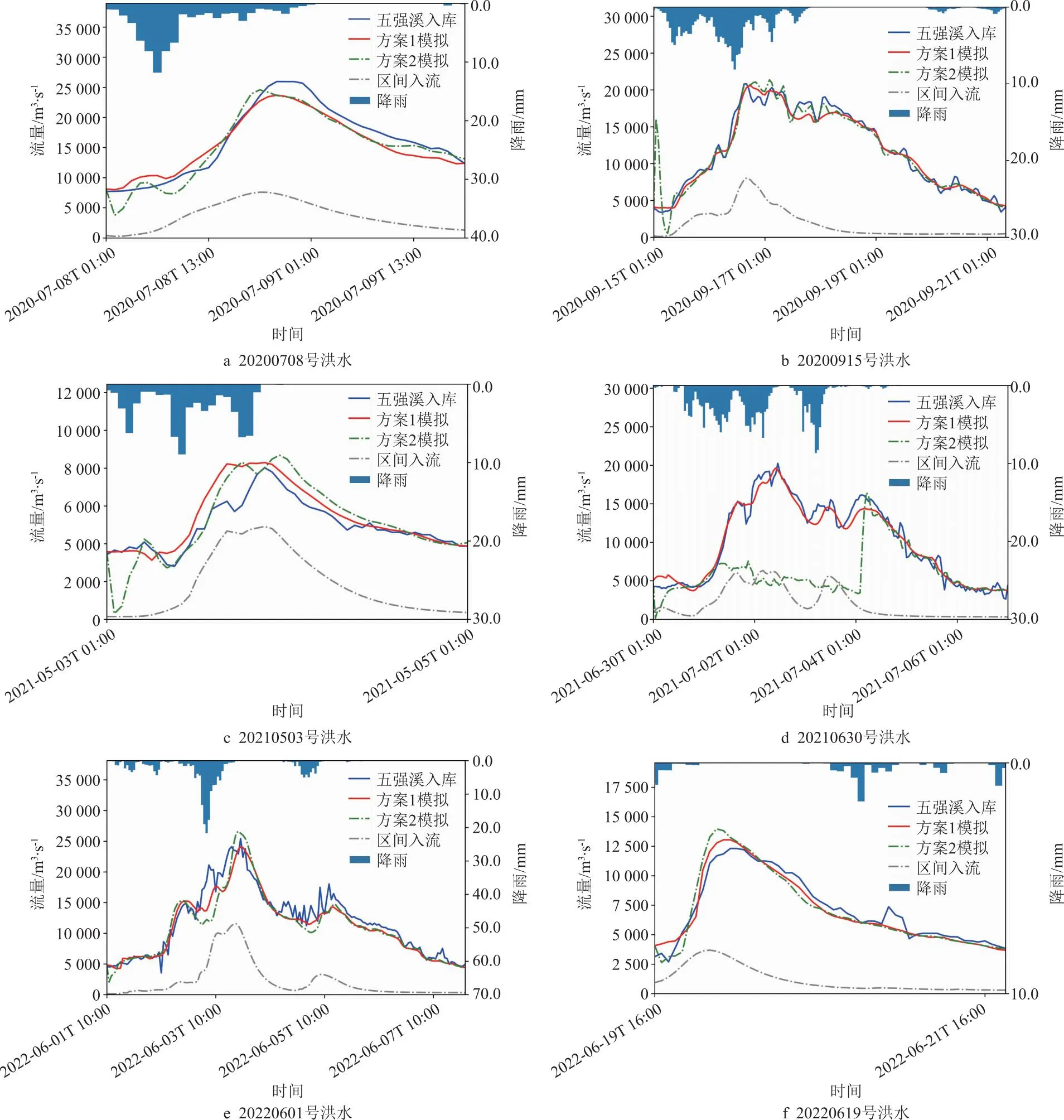
图5 不同汇流方案下模型模拟过程

2种汇流方案分别对应分段马斯京根法、分段马斯京根法和局地惯性波法组。其中五强溪入库流量是根据五强溪实测出库流量、坝上水位资料和五强溪水位库容曲线进行反推得到。由图5可知，2种方案在五强溪湿润流域模拟的洪水过程线与入库洪水均拟合较好。图中灰色过程线为五强溪子流域降雨后产生的区间入流，从图中可以得到，区间入流也是入库流量重要的一部分，模型产流参数的率定对其精度影响较大。其中，方案2中加入了基于水力学方法的局地惯性波法，在洪水开始前期，表现出陡涨陡落的不稳定情况，鉴于此，在进行后续模拟精度的计算过程中将洪水开始的前10 h作为预热期，而后进行精度计算，减小由于方法的结构性原因带来的不确定性。但方案2在20210630号洪水出现模拟异常状态，模拟洪水过程线与实际出现较大偏差。综上，2种方案的模拟情况较为满意，局地惯性波法在模拟精度和稳定性方面仍需进行深入分析讨论。

表6为两种汇流方案配置下新安江模型模拟精度情况。其中方案2在20210630号洪水中模拟出现异常状态，确定性系数为负值，方案2不予考虑此次洪水模拟情况。在2020年～2022年11场洪水模拟中，方案1、2的洪量合格率均为100%；洪峰合格率分别为100%、90%；峰现时间合格率分别为91%、90%。

表6 不同汇流方案配置下新安江模型模拟精度

由表6可知，方案1的平均洪量相对误差为2.95%，平均洪峰相对误差为6.47%，平均峰现时间误差为8.6 h，平均确定性系数为0.87；方案2的平均洪量相对误差为4.56%，平均洪峰相对误差为7.78%，平均峰现时间误差为10.6 h，平均确定性系数为0.85。

不同汇流方案配置下新安江模型模拟精度箱型，如图6所示。从图6可以看到，洪量模拟精度上方案1最优；洪峰模拟精度上，两个方案的精度集中情况比较相近，但方案2数据超出四分位数范围更多，四分位数范围即数据序列在25%～75%区间内，反映数据的集中情况；确定性系数情况上，在去除异常场次并设置一定时间的预热期后，方案1确定性系数稍优，但方案2较为集中。

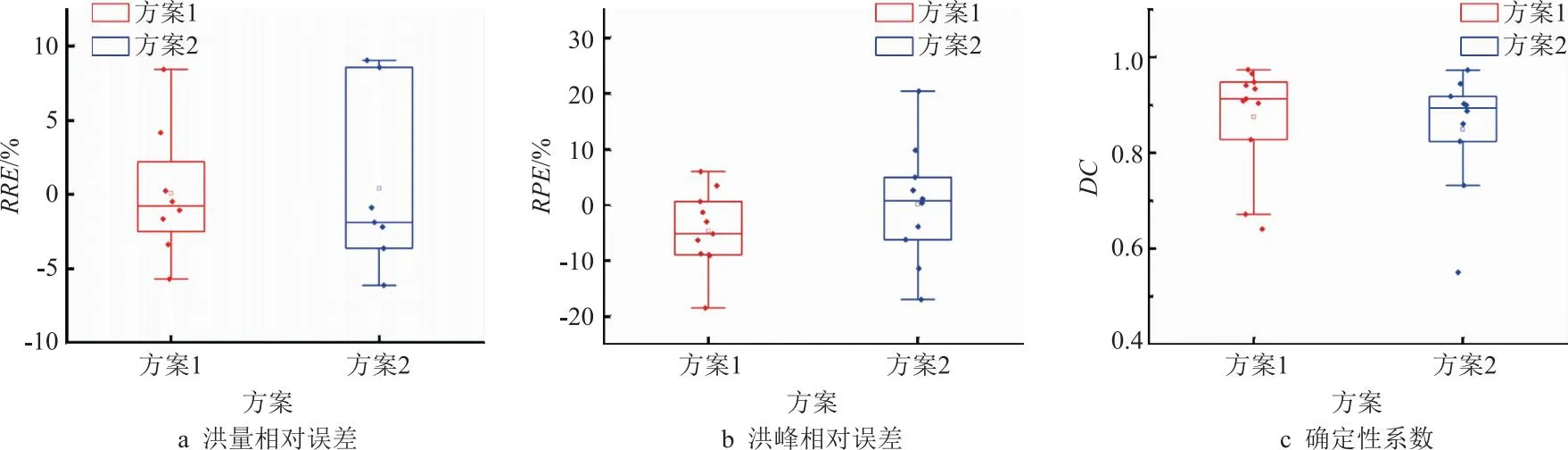
图6 不同汇流方案配置下新安江模型模拟精度箱型

总体上来看，方案1模拟精度更高，方案2模拟精度次之，在沅陵站～入库点进行局地惯性波法演算时，首先需要设置一定时间长度的预热期，使在进行演算时达到一个较为稳定的数据状态，但仍会出现计算不收敛的情况，这就增加了局地惯性波法的不稳定性问题。但方案2在20200708号、20200718号、20200824号、20200915号和20220619号5场洪水表现较好，且在前3场洪水模拟精度高于方案1，说明在靠近库区的回水段应用局地惯性波法具有一定的可靠性和适用性。

4 结 论

(1)对新安江模型配置不同汇流方案，结果表明分段马斯京根法仍是最简便、准确和稳定的汇流演算方法，模拟精度高且峰现时间误差低；靠近库区河道水面比降减小，库区河段水深增加，附加比降增大。在水库型河道中构建分段马斯京根法和局地惯性波法的汇流模块，具有一定的研究性，从结果来看，取得了较高的模拟精度，但不同流量和水位下的库区存在着不同长度的变动回水区，局地惯性波法的演算参数存在着不确定性，方法的稳定性和收敛性仍需进一步深入研究和解决。

(2)总体上来看，在湿润地区五强溪流域构建新安江模型是适用且准确的，模型配置不同汇流方案，取得了不同的模拟效果，但模拟精度均较高。汇流方案中加入局地惯性波法具有一定的创新性，为实时洪水预报提供了新的研究方案和路线。