基于λ-Bernstein基函数模型的拟合研究*

程文韬,沈苏琴

(安庆师范大学 数理学院,安徽 安庆 246000)

石油是全球性的重要资源,我国是主要石油消费国和进口国之一,随着国际油价的上涨和国内汽油价格的波动,需要建立健全石油风险规避机制。2004年8月25日,燃料油期货作为首个能源期货品种在上海期货交易所上市。何莹[1]研究了中国燃料油期货市场有效性及价格发现功能,我国燃料油期货自上市以来,其市场有效性和价格发现发挥的水平如何,一直是监管者和投资者十分关心的问题。

本文基于Bernstein基函数拟合模型[2-5],提出构造广义的Bernstein基函数拟合模型,即λ-Bernstein基函数拟合模型。选取某一时段燃料油期货收盘价格的数据资料,以拟合精度为要求,利用MATLAB,通过模拟构建λ-Bernstein基函数来拟合燃料油价格,并对拟合效果进行分析。

1 模型构建

1.1 λ-Bernstein基函数的确定

λ-Bernstein基函数[6-10]为

设原始时间序列数据为Yi,i=1,2,…,n,以λ-Bernstein基函数拟合的总体模型为

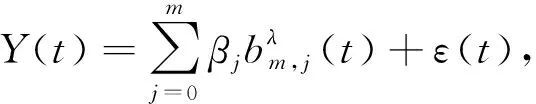
(1)

其中,βj(j=0,1,…,m)为系数矢量,在这里也称为拟合曲线的控制点;ε(t)是总体模型的误差项。

1.2 λ-Bernstein基函数建模

设参数化后时间序列数据为Y(t),0≤t≤1,以m次λ-Bernstein多项式

为基函数,构造总体模型为

(2)

拟合这一时间段的数据点,得到样本回归方程为

(3)

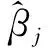
(4)

其中,e(t)为误差项。

枢纽锚固是在对外客运枢纽布局的基础上，充分发挥城市交通网络的功能，如道路、轨道交通等。在对外客运枢纽设计中，发挥锚固区域交通网络的作用，如高速公路、干线公路、城际公路、铁路以及公路客运班线等。因此，城市综合客运枢纽的锚固能够为人民群众出行的便捷性提供保障。

πi+1-πi=C。

为了整理方便,让πi取整数序列,即为

πi=i,i=1,2,…,n。

将参数化后的结果再进行规范化,即可得到规范参数化结果

以下采用规范参数化后的结果进行讨论。

采用最小二乘法[11]来确定拟合的曲线,并建立相应的模型。设所需的拟合曲线为

(5)

样本模型为

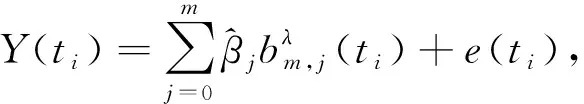
(6)

为求控制点βj(j=0,1,…,m),需使得

达到最小。

根据要求可以得到

(7)

1.3 模型改进

在用最小二乘法进行参数估计时,随着控制点个数m的增加,会出现严重的多重共线性,导致控制点的精度和稳定性下降。为了消除共线性,采用岭回归[12-15]来改进控制点的估计,设岭参数为k,则有

其中,I是m+1阶单位矩阵。选择合适的岭参数k,即可保证控制点的估计值具有较好的有效性。

2 实例分析

2.1 参数的选取

根据第1部分构建的模型,对2011-2022年燃料油期货收盘价格的月数据进行分析,用岭回归对参数估计进行改进,为此虽牺牲了部分拟合精度,但消除了共线性,提高了结果的准确性。岭参数k根据(8)式选取。

(8)

其中,λmax和λmin分别是设计矩阵BTB的最大特征值和最小特征值。

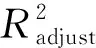
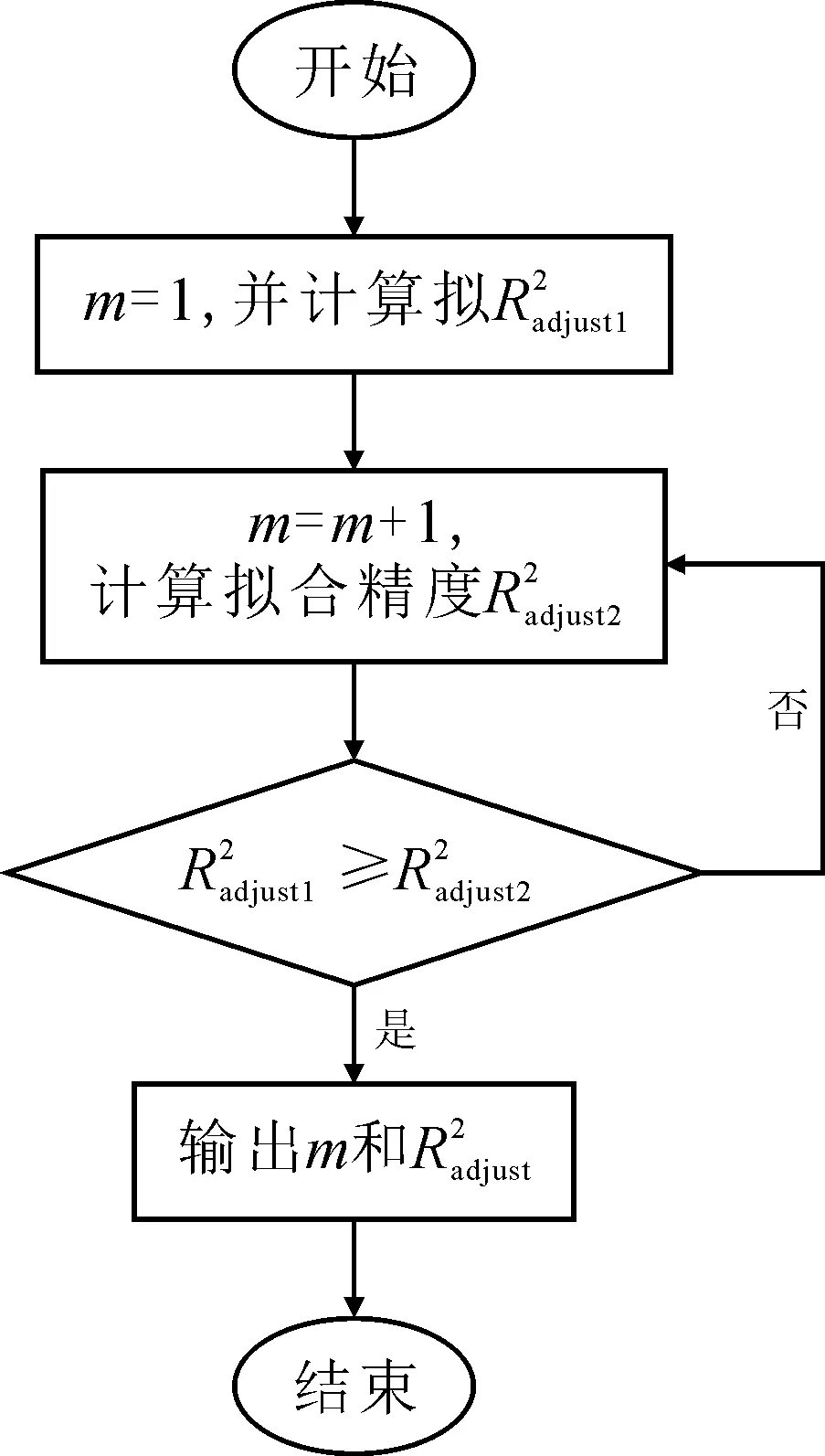
图1 基函数建模流程图Fig. 1 Basis function modeling flowchart

2.2 燃料油收盘价建模

2011-2022年燃料油期货收盘价格的原始数据如图2所示。

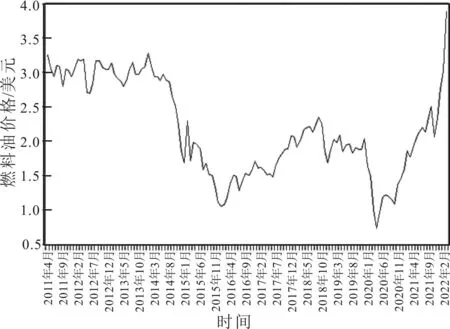
图2 原始燃料油时间序列的变化图Fig. 2 Diagram of time series of original fuel oil

根据第1部分的模型以及2.1节选取的参数,得到控制点的估计值,如表1所示。

表1 控制点的估计值Tab. 1 Estimates of control points

因此,由控制点的估计值得到拟合曲线如图3和图4所示。图3为最小二乘估计得到的拟合曲线,其调整的拟合优度达到95%,但存在共线性。图4为岭估计得到拟合曲线,减少了共线性的影响,其调整的拟合优度达到90%,结果稳定性更高。由于数据不光滑且有个别离群点,一定程度上会影响拟合精度。

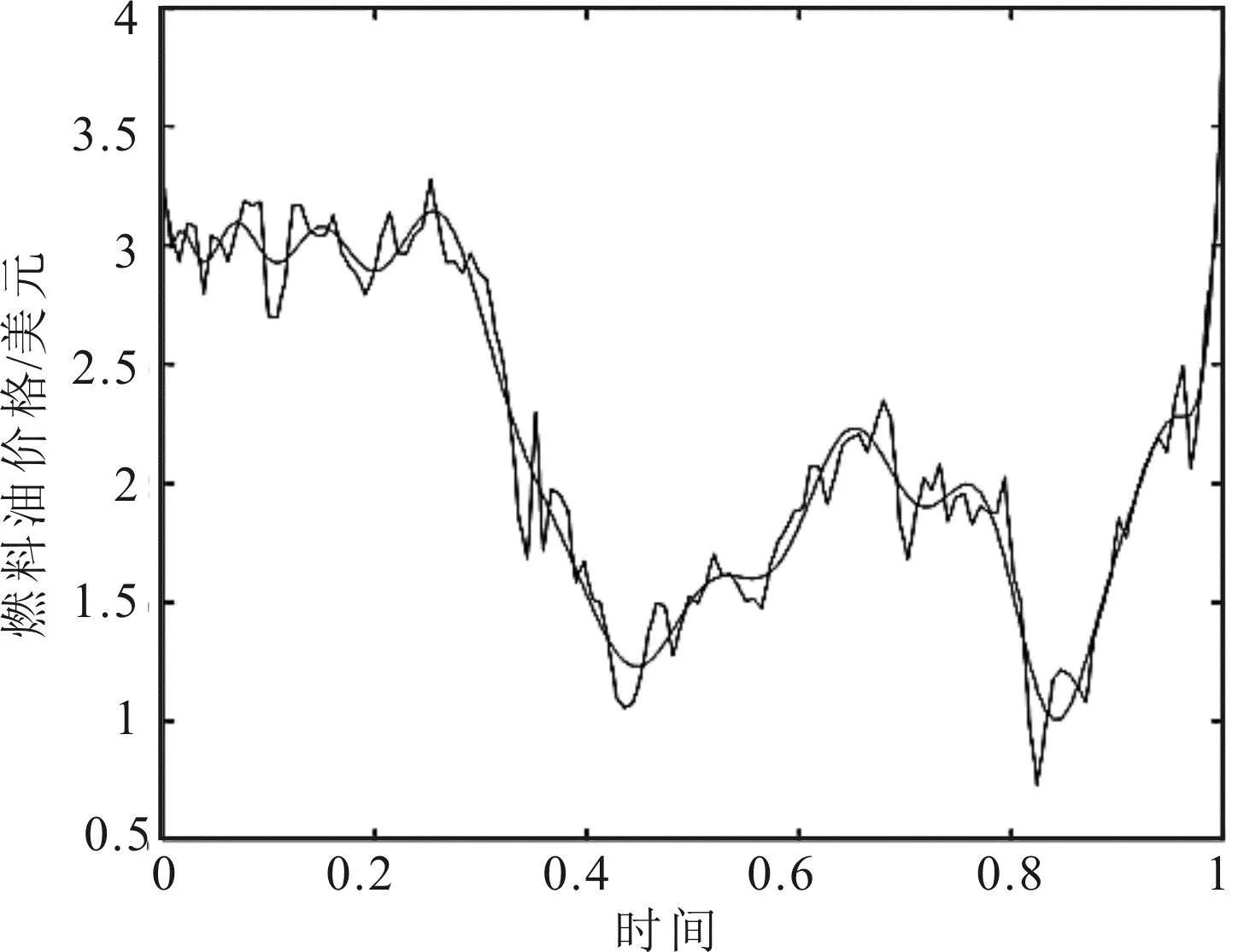
图3 最小二乘拟合结果Fig. 3 Least squares fitting results

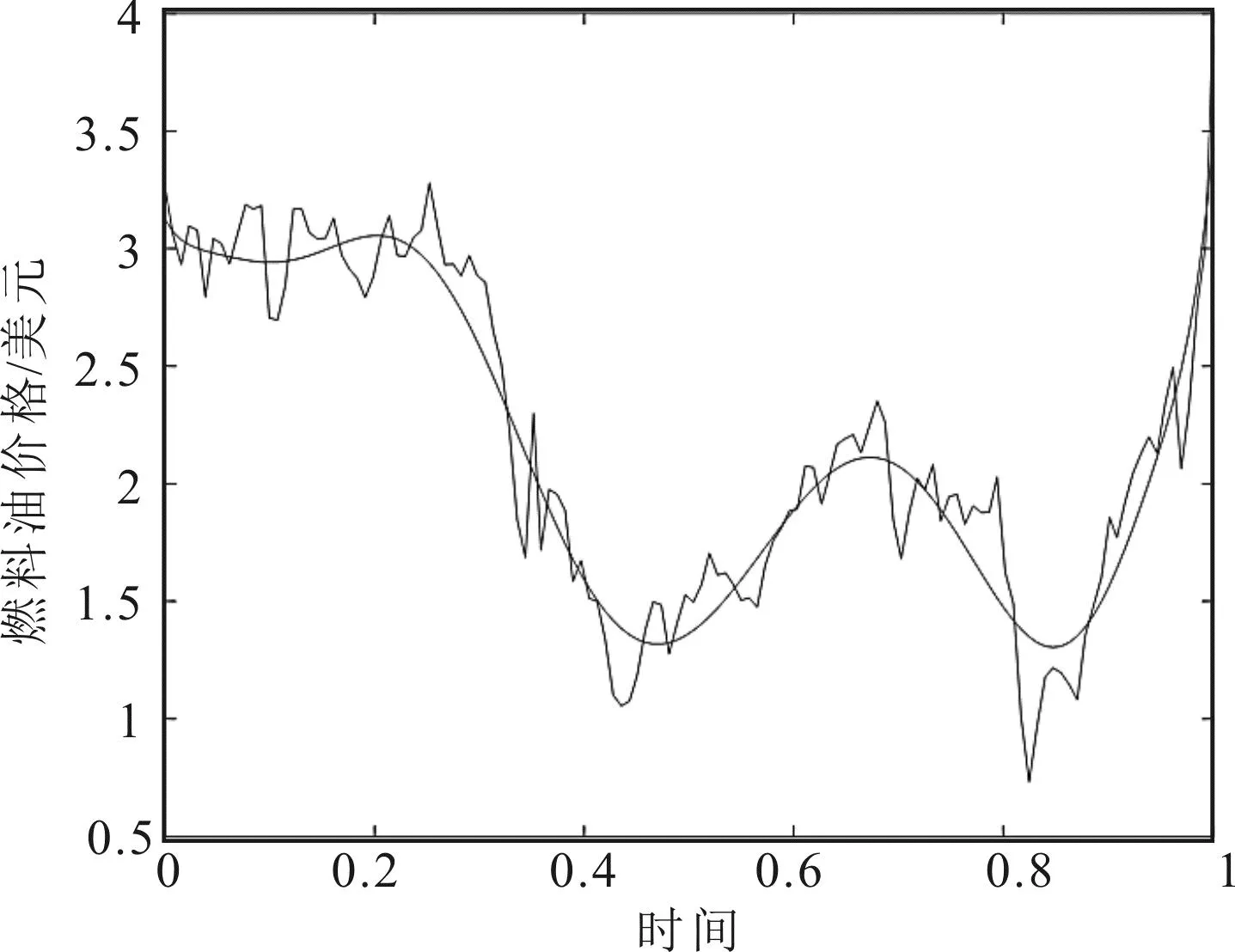
图4 岭回归拟合结果Fig. 4 Ridge regression fitting results

由此绘制残差比图像,如图5和图6所示。图5是图3中拟合曲线和实际曲线的误差图,图6是图4拟合曲线和实际曲线的误差图。图5误差范围小,但结果稳定性低;图6误差比图5稍高一点,但结果稳定性高。图中极个别点误差较大是由于数据不光滑导致的,若选取光滑的数据,精度会提高,误差会更小。

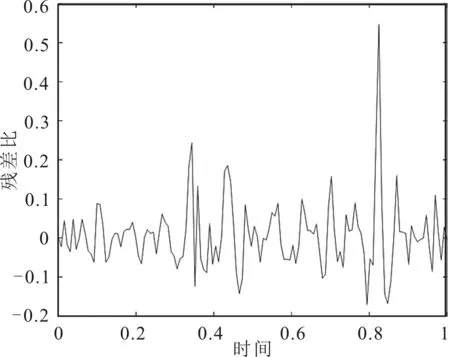
图5 最小二乘—残差比图Fig. 5 Least squares-residual ratio graph

图6 岭回归—残差比图Fig. 6 Ridge regression-residual ratio chart

3 总结

本文在传统Bernstein基函数模型的基础上,推广得到λ-Bernstein基函数模型,λ-Bernstein基函数模型的优势在于可通过调整模型参数λ的大小,控制拟合曲线的形状,从而提高拟合精度,且实证出λ取-1时比λ取0时,拟合效果更好,即λ-Bernstein基函数模型的灵活性和拟合精度均比原有的Bernstein基函数模型好。