基于GF(2m)域上Ⅱ型最优正规基的模乘算法及实现∗

高 照 王庆年 樊 荣

（中国船舶集团有限公司第722研究所 武汉 430205）

1 引言

椭圆曲线密码体制（ECC）自出现以来，由于其安全性更高、计算量更小等特点，引起了人们的关注与研究。在椭圆曲线密码体系的应用中，通常采用基于素数域或伽罗华域（二进制域）上的椭圆曲线点群，特别是GF(2m)域上的算法，易于硬件实现。

在有限域的运算中，乘法是极其重要的一部分。二进制域上最普遍使用两种基：多项式基和正规基。其中正规基上的乘法较为缓慢且代价为多项式基的两倍以上。但在正规基上的平方运算只需要进行移位，远远优于多项式上的平方运算。因此正规基一般只在某些特殊情况下使用：硬件面积要求小，平方运算多或乘法运算较少。

本文主要研究二进制域上的正规基模乘运算，通过一种变化，使得正规基能够使用多项式基的方法进行乘法运算，并在FPGA 中实现。结果表明，此方法比起传统正规基算法效率提高且资源占用更少。

2 背景知识

2.1 Ⅱ型最优正规基和重序正规基［1］

假设β是GF(2m)上m次不可约多项式的原根，如果集合中的元素互相线性无关，则集合N是GF(2m) 上的一组正规基。对于∀a∊GF(2m)有

对于任意的m，正规基总是存在的。高斯正规基是一种特殊类别的正规基，因其乘法运算更简单、更有效，又可称为低复杂度正规基。高斯正规基的特征值T是个衡量该基乘法复杂度的正整数。除了能被8 整除的m，二进制域GF(2m)中均存在高斯正规基。特征值T为1和2的高斯正规基被称为最优正规基，分别被称为I 型最优正规基和II型最优正规基。

两种正规基的差别在于定义中所采用的数学公式不同。但出于安全角度的考虑，Ⅰ型最优正规基已经被许多安全标准排除在外，如NIST ECDSA和ANSI X9.62。而Ⅱ型最优正规基由于其更好的安全性，被广泛应用推广及使用在密码算法应用中。判断GF(2m)中是否存在II 型最优正规基可以用如下定理［2］：

定理1 如果m不能被8 整除，且2m+1 是素数，且下面两个条件之一成立：

1）2是模2m+1的原根；

2）2m+1 是模4 为3 的一个素数，并且2 模2m+1的次数为m。

则β=γ+γ-1可生成一组GF(2m)上的Ⅱ型最优正规基，其中γ为2m+1次本原单位根。

2.2 正规基到Ⅱ型多项式的转换

文献［5］和文献［6］研究了多项式基与正规基之间的联系，以及它在实现正规基高性能乘法中的应用。文献［6］中描述了如何利用高斯生成正规基进行乘法，并进一步将乘法简化为多项式乘法。文献［7～8］则在前面的基础上，提出了一种将正规基通过线性变换转到多项式基后相乘，再将乘积通过线性变换的逆过程转变回正规基的算法。文献［8］将这种新的多项式基称为Ⅱ型多项式基。

以GF(25) 为例：重序正规基为={γ+γ-1,γ2+γ-2,…,γ5+γ-5}，其中：

文献［8］中将P称为Ⅱ型多项式基，文献［7］中证明了可以利用线性变换使得转变为P，并且P上可以使用任何适用于普通多项式的乘法算法。但文献［7］中先将扩展到={1,γ+γ-1,γ2+γ-2,…,γm+γ-m}，然后变换到P'={1,γ+γ-1,(γ+γ-1)2,…,(γ+γ-1)m}。这种扩展使得原本的m项的乘法变为m+1项。

文献［8］在前者的基础上提出了改进，给出了如下变换：

向量e∊，ei为e中第i个元素，i∊{1,2,…,k}，e=(e1,e2,…ek)。当i不在{1,2,…,k}范围内时，ei=0。对于每个k≥1 定义一个转换函数，规则如下：

1）T1(e)=e。

2）当k≥2 时，j为在{1,2,…,k-1} 中最大的2 的幂。将向量e分为f和g，f=(e1,e2,…ej)，g=(ej+1,ej+2,…ek)，得到一个新的向量ℎ，ℎi=fi+gj-i。

通过T变换，就能使得重序正规基变换到Ⅱ型多项式基

3 基于基转换的正规基模乘算法

设GF(2m)中的重序正规基={γ+γ-1,γ2+γ-2,…,γm+γ-m} 和Ⅱ型多项式基P={γ+γ-1,(γ+γ-1)2,…,(γ+γ-1)5}。两者间的关系为

其中Tm为m阶转换矩阵，可由T变换得到。

对于任意a,b∊GF(2m)及其乘积c∊GF(2m)，以排序正规基表示：

令z=γ+γ-1，结合式（3～5）可得a,b在多项式下的表示为a',b'：

将式（6）、（7）两个m项多项式相乘，得到一个2m-1项的多项式：

将(p2m,…,p3,p2) 补充为(p2m,…,p3,p2,0)，然后通过逆变换得到c'：

由此便得到了a×b的结果c=(cm,…,c2,c1)。

4 基于基转换的模乘算法的改进

T变换生成的转换矩阵Tm是一个上三角矩阵，如图1所示，因此逆变换对应的矩阵也是一个上三角阵。约减的过程也可以看成是向量乘上一个约减矩阵R，约减矩阵如图2所示。

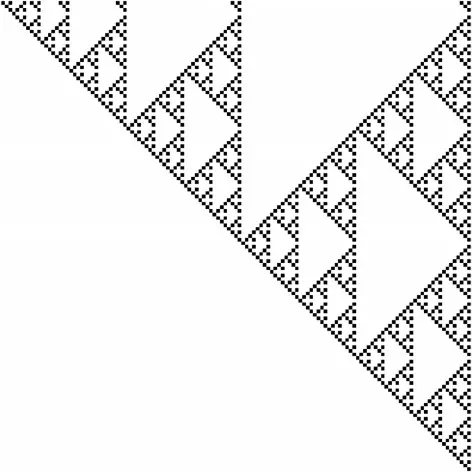
图1 m=131的转换矩阵

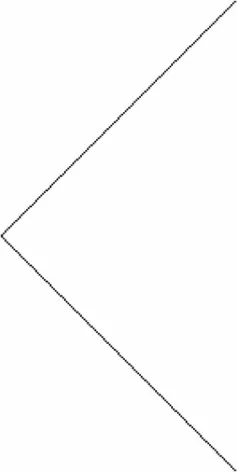
图2 m=131约减矩阵

另外在多项式乘法上，选择使用改进的karatsuba 算法。原karatsuba 算法是将m项多项式扩展为m+1 项或缩短为m-1 项后进行二分，改进思路则是将m分解为m=2k+d，然后再对2k进行二分：

对于多项式A=a1x+a2x2+…+amxm，将其分为

由此，多项式A与B相乘等于

其中AL和BL为2k项多项式。然后再对AL和BL进行半分，即

其中n=2k，对ALH和ALL继续半分，直到分为小于等于6项时停止。

将改进后karatsuba 算法同改进后的转换算法合并，得到的过程如下：

1）通过式（1）将a,b的正规基表示转换为重序正规基。

2）计算a'=(am,…,a2,a1)×Tm和b'=(bm,…,b2,b1)×Tm。

3）由a',b'算出多项式p=p2mz2m+…+p3z3+p2z2。

4）计 算c=(p2m,…,p3,p2,0)×TR=(cm,…,c2,c1)。

5）利用式（1）将c由重序正规基排回正规基。

5 改进后的性能优势

改进后整个计算过程涉及到两次排序（正规基与重序正规基）、两次矩阵乘法和一次m项的多项式相乘。其中排序时，因为两种基（正规基和重序正规基）之间是一一对应关系，所以不占用任何资源。Tm变换所需要的XOR 运算为而多项式计算需要的运算XOR 和AND 为M(m)，取决于所采用的方法。约减则因为我们将逆变换和约减部分合并后省去。所以整个算法过程所需要的XOR 和AND 运算约为，相比于原算法节省了m。

多项式计算上使用改进后的karatsuba 算法，改进后需要2d(2k+1)-1 个XOR 和2d2k个AND，故整个计算过程需要的XOR 和AND 运算为

常用的高斯正规基算法还有IEEE 规定的标准算法［9］、Massey-Omura［10～12］、Τeoplize 矩阵［13～14］以及ΤMVP［15］等，所需的算法复杂度如表1所示。

表1 不同算法性能比较

本文设计上可以看成是一个多项式乘法加上两次基转换，因此可以看到，相比于其他传统的正规基乘法，即使多项式乘法上采用直接相乘，即M(m)=2m2，本文的设计在复杂度上也是更低的。

6 实现与测试

为了验证本文改进算法的正确性并对其资源开销及其运算性能进行评估，我们选择在GF(2131)和GF(2233) 两条曲线上进行实现。硬件选型为Xilinx Artix-7 FPGA（XC7A50T-1FTG256C），进行实际验证与测试。

图3、4 分别为GF(2233)上实现的乘法器的RTL原理图以及仿真结果。另外，我们以100MHz时钟频率进行综合，并将结果与将正规基基转换到普通多项式基后进行模乘，再将结果转回正规基的方法进行对比。结果如表2所示，由于从重序正规基到Ⅱ型多项式的变换是线性的，与正规基到普通多项式基的转换矩阵不同，因此LUTs的数量减少了近40%。

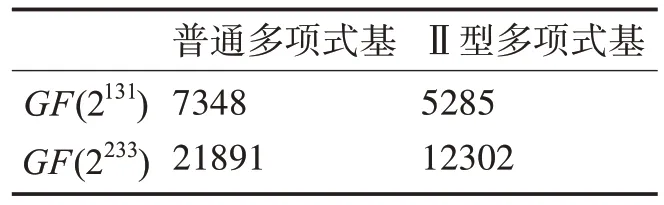
表2 综合后LUTs数量对比

图3 233bit乘法器RTL原理图

图4 233bit乘法器仿真结果

此外，文献［15］中实现了m=255 的乘法器，LUTs数量为19997。尽管我们只在m=233 上实现乘法器，但与其支持位宽较为接近，且LUTs数量仅仅是其60%。因此我们估计在位宽相同情况下，本文所设计的乘法器将优于前者。

7 结语

本文介绍了最优正规基、排序正规基、Ⅱ型多项式等相关概念，在现有算法基础进行改进，提出了新的Ⅱ型最优正规基乘法方案，并在GF(2131)和GF(2233)两条曲线上进行了实现。从算法复杂度和综合后的结果来看，本文设计相比于其他正规基乘法算法实现了较大的提升。