求解三维裂缝型多孔介质流体的场分裂预条件子研究

杨念 杨海建,* 邵柏强

(1.湖南大学重庆研究院,重庆,401120;2.湖南大学数学学院,长沙,410082)

1 引言

由于采用高分辨率网格进行流动模拟可以捕捉精细尺度现象,因此它常用于对复杂地质流体的物理现象进行精确描述.例如裂缝型油藏问题,在模拟过程中连通的裂缝只占据很小的计算区域,但可以完全控制从毫米到数百公里的流动过程[1].为了模拟长时间的移动过程和多尺度的复杂地形,往往需要利用非常多的网格块进行全尺度计算[2,3],这使得完成预测可能需要数周甚至数月的时间[4,5,6].对于如此复杂、非线性的流动问题进行大规模模拟,需要的计算资源非常大.因此,为了提高计算效率必须建立能够充分利用大规模并行计算机优势的并行流场模拟器或求解器.

对于大型非线性方程组,Newton-Krylov 算法[7,8,9]是一种具有快速局部收敛特性的通用迭代求解方法.这种迭代方法可以在一些流行的开源库中找到,如PETSc[10],NITSOL[11].由于Jacobi矩阵的高度非对称和病态,在求解非线性系统时的一个主要瓶颈是如何在每次Newton 迭代时保证对线性系统预处理的鲁棒性和高效性.如果没有适当的预条件子,Newton-Krylov 算法可能不会有良好的收敛速度.因此,即使有超级计算机系统和大量的计算核心可用,也不能减少计算时间.一种重要的Newton-Krylov 预处理器被称为场分裂(FS)预条件子,它将原始系统划分为一系列简化的隐式系统.FS 预条件子具有块结构,使用物理变量作为拆分策略,然后应用不同的预处理器来处理具有不同属性的变量.因此,用不同方法从原始系统矩阵中提取块,可以得到不同的预条件子,如加性FS 预条件子[12,13]、乘性FS 预条件子[14]、舒尔补FS 预条件子[13,15]和约束压力残差(CPR)预条件子[16,17,18].加性或乘性FS 方法是基于Jacobi 或Gauss-Seidel 方法,分别将耦合问题分解为一系列更简单的问题.舒尔补FS 方法也是为利用不同耦合过程的特性设计的.约束压力残差预条件子是Wallis 在1980 年代初提出的[17],是一个行业标准的求解器,已成功应用于各种流动问题[12,13,14,18,19],包括油藏模拟和计算流体动力学.

本文研究基于物理和区域分解方法的不同组合的FS 预条件子,应用于裂缝型多孔介质中的非定常流体问题[1,4].在该算法中,FS 预条件子中的所有子系统都采用基于RAS 的具有多层重叠的域分解技术进行求解,构造包括稀疏LU 或ILU 分解在内的不同子域求解器,并对其进行详细比较.为了进一步提高算法的鲁棒性和可扩展性,并节省计算时间,本文利用几何多重网格框架构建一种两水平FS 预条件子,通过粗网格校正,获得粗网格和细网格之间附加的子域间信息,以解析误差的低频分量.数值实验表明,所提出的预处理方法在超级计算机上对某些地下流动问题具有高度的可扩展性.

本文安排如下:在第2 节中介绍裂缝型多孔介质的双孔双渗模型;在第3 节中,给出基于物理和区域分解方法的不同组合的FS 预条件子,并将对应的算法应用于求解所得到的非线性系统;在第4 节中进行数值实验来检验所建立算法的效率和有效性;最后在第5 节对本文进行归纳总结.

2 裂缝型多孔介质双孔双渗模型

本节介绍描述裂缝型多孔介质中的油藏流动的双孔双渗(DPDP)模型[1,4].在该模型中,基质和裂缝被视为两个独立的连续体,通过界面相互连接并允许它们转移.DPDP 模型的质量平衡方程为

其中,ϕα为基质和裂缝的孔隙率,ρα为流体密度,uα为达西速度,Kα为渗透率张量,pα为多孔介质的压力,µ为流体的粘度,g为重力矢量,计算域为Ω⊂Rd,最终模拟时间为Te.此外,τ和q分别为转移项和生产项,计算式如下:

其中,Lx,Ly和Lz分别表示x,y,z方向上的裂缝间距,θ是一个与生产井位置有关的常数,re是排水半径,rw是井半径,pb是井底压力,pv是井周围的平均裂缝压力.

利用Peng-Robinson 状态方程(PR-EoS,[5,20])将多孔介质中可压缩流体ρα的密度描述为温度和压力的函数:

其中,W,R和T分别为分子量、通用气体常数和温度.气体压缩系数Zα由下式计算:

这里,PR-EoS 参数Aα和Bα定义如下:

其中,Tc和pc分别为气体临界状态下的温度和压力,b是如下的分段函数:

其中,Tb是沸点温度,patm是大气压.

针对上述问题,本文使用混合有限元(Mixed Finite Element,MFE)方法进行空间离散,用显式第一步、单对角系数、对角隐式Runge-Kutta 格式进行时间离散(详见参考文献[21]).式(2.1)的完全离散形式是一个具有未知数(p1,p2)的非线性代数方程组:

3 Field-Split 预条件子

本节介绍求解非线性代数系统的Newton-Krylov 算法,并在Newton-Krylov 算法中,构建几种基于物理和区域分解方法的的场分裂(FS)预条件子.

3.1 Newton-Krylov 算法

首先介绍求解非线性代数方程组(2.2)的Newton-Krylov 算法[7,8,9],记未知量组成的向量为X=(x1,x2,···,xl)∈Rn,残差向量为F(X)=(F1(X),F2(X),···,Fi(X))T∈Rn.设(2.2)对应的Jacobi 矩阵为:

假设初始向量为X0∈Rn,第k次Newton 迭代的近似解为Xk,则第k+1 次Newton 迭代的近似解为:

其中,dk是用Krylov 迭代法[22]求得的搜索方向,λk∈(0,1]是由三次线搜索确定的步长.由此可得到求解(2.2)的迭代形式:

其中,∇F（Xk）为Jacobi 矩阵(3.1),满足以下条件:

其中,ηr∈[0,1)是线性迭代的相对误差,ηa∈[0,1)是线性迭代的绝对误差.迭代过程的终止条件为:

其中,εr和εa分别是Newton 迭代的相对误差和绝对误差.

在Newton-Krylov 算法中,求解器最重要的部分是选择合适的预条件形式:

3.2 场分裂预条件子

场分裂预条件子的方法是使用域松弛或域分解来求解l×l线性块系统.为简单起见,将线性块系统限制为2×2 块,即(3.1)中的Jacobi 矩阵为:

本文给出四种场分裂预条件子,即加性FS 预条件子、乘性FS 预条件子、舒尔补FS 预条件子和CPR 预条件子.

加性FS 预条件子和乘性FS 预条件子分别为:

舒尔补FS 预条件子为:

其中,C=J22-.舒尔补FS 预条件子的逆可以写成以下形式:

并且舒尔补FS 预条件子可以全分解为LDU形式,通过去掉某些项得到预条件子的几种变体,如下三角(LD)-1,上三角(DU)-1和对角线等类型.注意,对角线“diag”类型具有以下形式:

在实际中,C的近似值有以下几种形式:“a11”类型C-1=;“selfp” 类型C-1=(J22-J21(diag(J11))-1J12)-1;“full”类型C-1=.

第四种FS 预条件子是约束压力残差预条件子(CPR 预条件子).利用CPR 预条件子求解方程是一个两阶段过程:首先通过消除某些变量求解一个较小的简化系统,然后近似求解原始的完整系统.第一阶段预条件子为:

在两水平FS 预条件子中,粗网格主要用于信息交换.在定义的粗网格上需要求解以下线性问题:

由于一些直接求解方法在大规模仿真应用中计算成本较大,所以采用一水平FS 预条件子的GMRES 方法.当用迭代法求解粗线性系统时,整体的预条件子是一个迭代过程,且预条件子在每次迭代中都有变化.因此,使用两水平FS 预条件子求解线性系统时,采用柔性GMRES(fGMRES)方法.

3.3 限制加性的Schwarz 预条件子

在FS 预条件子中,用限制加性Schwarz(RAS)算法来近似对应变量Jacobi 矩阵的逆.假设待求解的原始系统AX=b有N个未知数和N个线性方程.在定义RAS 预条件子之前,先介绍区域Ω 的一种分解方式.首先将区域Ω 分解为Np个互不重叠的子区域Ωi,i=1,2,3,···,Np(Np为处理器的个数),然后将每个子区域Ωi向外扩张δ层网格,得到重叠子区域Ωi,δ,其中δ为子区域的重叠参数.图1是区域Ω 的某一分解方式,其中灰色实线表示网格线,黑色实线表示区域Ω 的非重叠划分方式,深灰色区域为某一非重叠子区域Ωi,0,浅灰色区域为该非重叠子区域Ωi,0向外扩张的δ=2 层网格.设Ni和N分别是区域和Ω 内的自由度.定义限制性算子Ri,δ∈,该矩阵的元素定义为:若1≤l1≤Ni和1≤l2≤N,对应于子区域Ωi,δ内的同一个网格点,则该元素的值取为1,否则为0.

限制加性Schwarz 预条件子定义为:

其中,Ri,0的定义与Ri,δ类似,当且仅当其对应的网格点在区域Ωi内时,矩阵元素的值为1.(Ai,δ)-1是子域Jacobi 矩阵Ai,δ的近似逆,它是由稀疏LU 或ILU 因子分解[22]计算出来的.

4 数值实验

本节将进行一系列数值实验来评估所提出的场分裂预条件子的性能.本文研究的算法使用开源的可移植、可扩展的科学计算工具包(PETSc)[10]来实现,数值测试在天河2 号超级计算机上进行.在以下测试的表格中,“N.It”表示每个时间步的Newton 迭代次数的平均值,“L.It”表示每次Newton 迭代一水平或两水平FS 预处理GMRES 迭代的平均次数,“Time”是总计算时间(以秒为单位),“Np”表示处理器核心的数量.

4.1 算例一:抛物型渗透率

在算例一中,油藏的计算域是Ω=(0 m,50 m)3.如图2(a)所示,在基体中,高渗透带位于(y≥0.16x2-7.78x+112.22)[23],渗透率为100 md(图中红色部分),其他为低渗透带,渗透率为1 md;裂缝中的渗透率值比基体中的渗透率值大100 倍,裂缝孔隙率为0.001,基体孔隙率为0.05;初始压力随深度的变化而变化,设定在10∼11Mpa 之间;注水井和生产井的井底压力分别为12Mpa和8Mpa.图(b)–(d)为不同时刻裂缝压力分布图.

图2 算例一中渗透率分布图和不同时刻裂缝压力分布图

表1显示了加性FS 预条件子和乘性FS 预条件子在不同子域求解器和重叠因子下的测试结果能.在测试中,网格大小固定为64×64×64,处理器的数量为Np=8,时间步长∆t=0.1 天,计算5 个时间步.测试结果表明:(a)LU 子求解器在线性迭代方面优于ILU 子求解器,而ILU 子求解器在计算时间方面有优势;(b)重叠因子越大,线性迭代次数越少,但由于通信成本增加,计算时间不一定减少.为线性迭代和计算时间之间的平衡,在接下来的测试中,我们固定一个最优参数组合为重叠因子δ=1 和求解器ILU(1).

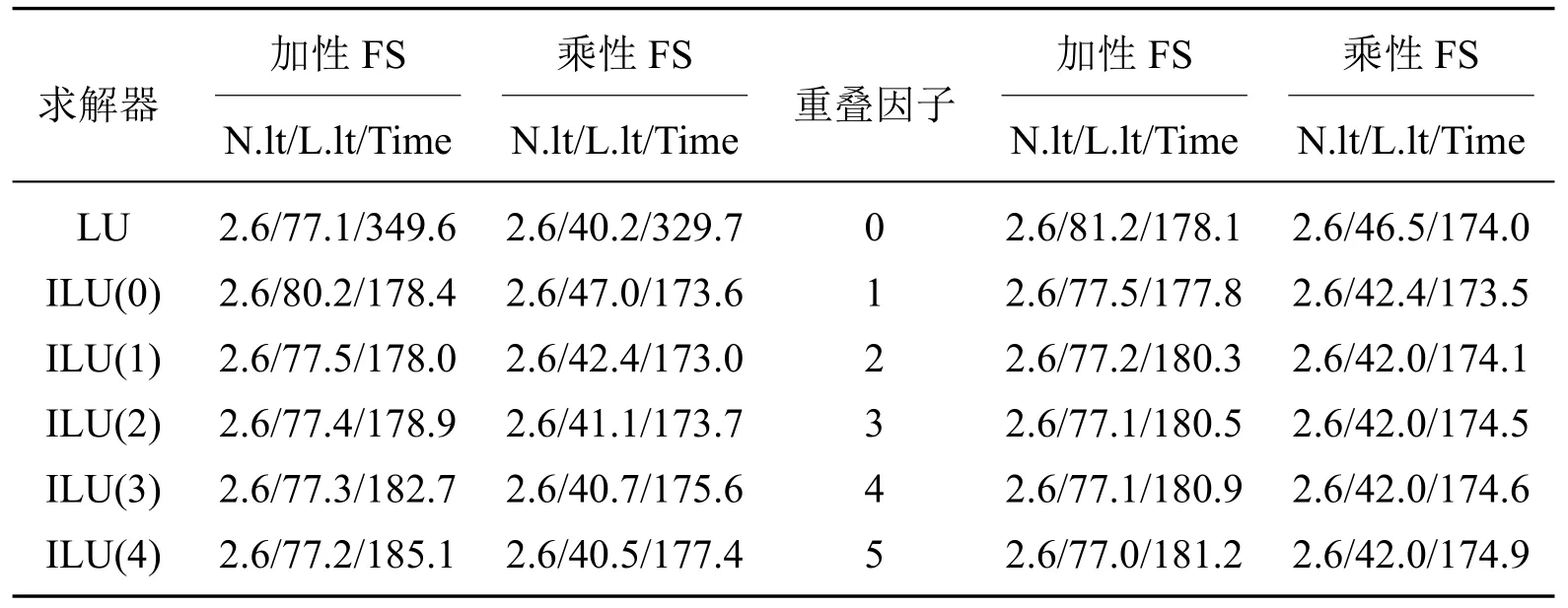
表1 算例一中不同子域求解器和重叠因子对加性和乘性FS 预条件子的影响

表2显示了在“full”类型的近似块分解下,舒尔补FS 预条件子在不同预处理类型下的性能.而表3显示了在舒尔补FS 的预处理类型固定为“a11”时,使用不同的近似块分解时预条件子的性能的测试结果.测试结果表明:(a)线性迭代次数对网格尺寸不敏感;(b)预处理类型和近似块分解的选择对舒尔补FS 方法的鲁棒性和效率有很大影响;(c)在舒尔补FS 预条件子中,“a11”预处理类型和“full”类型近似块分解的组合是一个用于接下来的数值试验的最优选择.舒尔补FS 预条件子的线性迭代次数非常少,主要原因是“lower”类型或“upper”类型的舒尔补FS 预条件子具有1 或2次最小多项式,一般在2 次线性迭代后收敛.从图4从可以看出,舒尔补FS 预条件子可以将Jacobi矩阵的特征值很好地限制在1 附近,因而线性迭代次数少.

表2 算例一中不同预处理类型对舒尔补FS 预条件子的影响(“∗”表示计算两小时仍无结果)

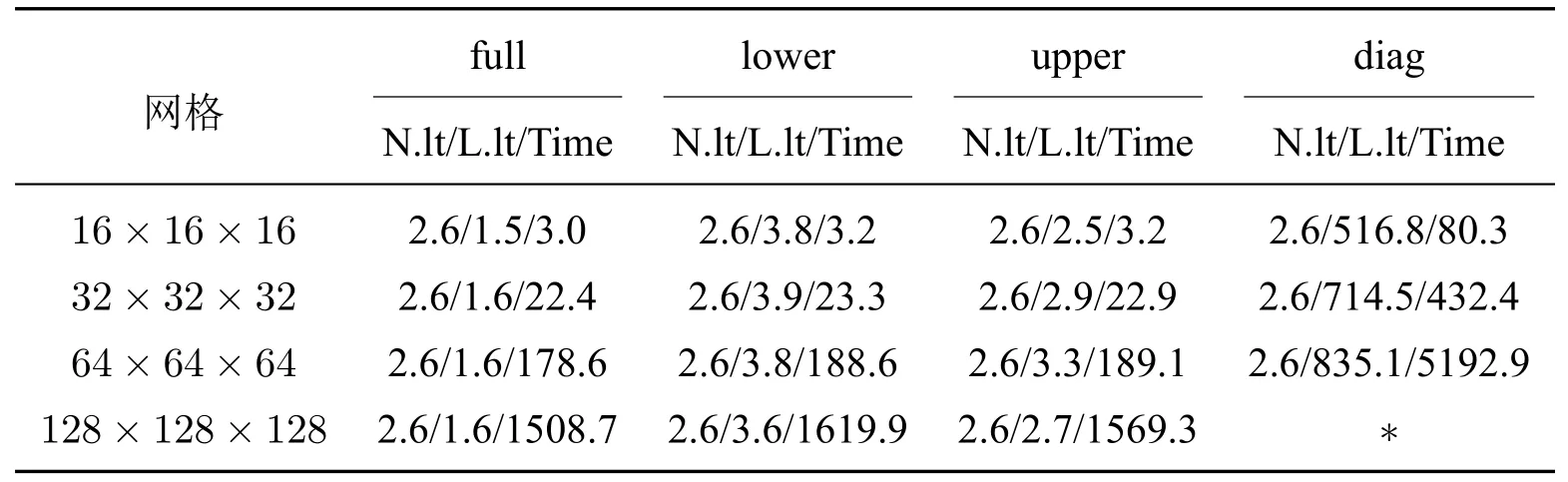
表3 算例一中不同近似块分解对舒尔补FS 条件子的影响(“∗”表示计算两小时仍无结果)

4.2 算例二:阶梯型渗透率

在算例二中,油藏的计算域是Ω=(0 m,800m)×(0 m,800m)×(0 m,400m).如图3所示,基质中的红色区域为高渗透区,渗透率为100md,蓝色区域为低渗透区,渗透率为1md;裂缝中的渗透率值比基质中的渗透率值大100 倍;基质中的孔隙率值为0.2,比裂缝中的孔隙度大10 倍.注水井和生产井的井底压力分别为12Mpa 和8Mpa.

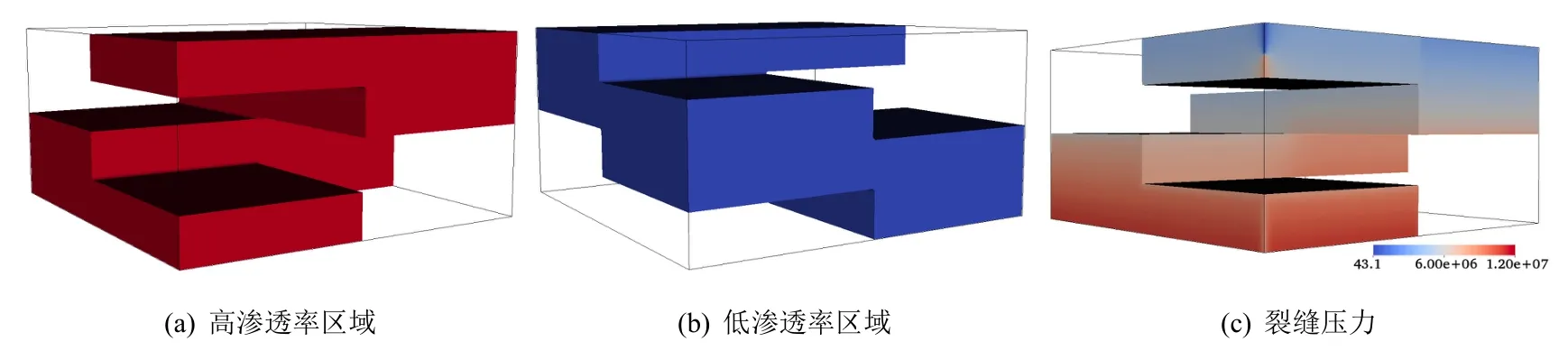
图3 算例二中渗透率分布图和压力分布图

采用一水平的FS 预条件子求解上述DPDP 模型,表4显示了几种不同FS 预条件子在不同网格尺寸下的线性迭代和计算时间方面的性能.表中“CPR-p1”表示第一级预处理条件子(3.8)中的构造基于基质压力p1,依此类推.从表4可以看出:(a)舒尔补FS 预条件子需要的GMRES 迭代次数最少;(b)加性FS、乘性FS 和CPR-p2预条件子的性能在线性迭代方面具有相似的数值结果;(c)平衡线性迭代和计算时间最优预条件子为CPR-p1.

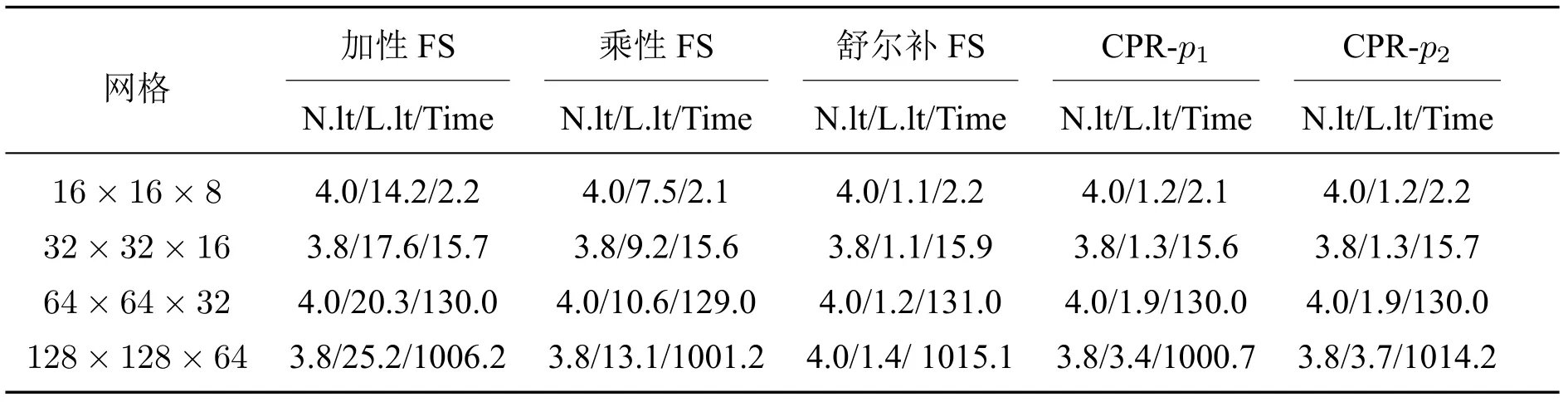
表4 算例二中不同FS 预条件子性能的比较

图4使用16×16×8 的网格绘制了该问题的原始Jacobi 矩阵和具有不同FS 预条件子的预处理矩阵的特征值.从图中可以看出原始Jacobi 矩阵的特征值是非常分散的,在使用场分裂预条件子处理后特征值的分布聚集度高,并且CPR-p2预条件子的效果最好.

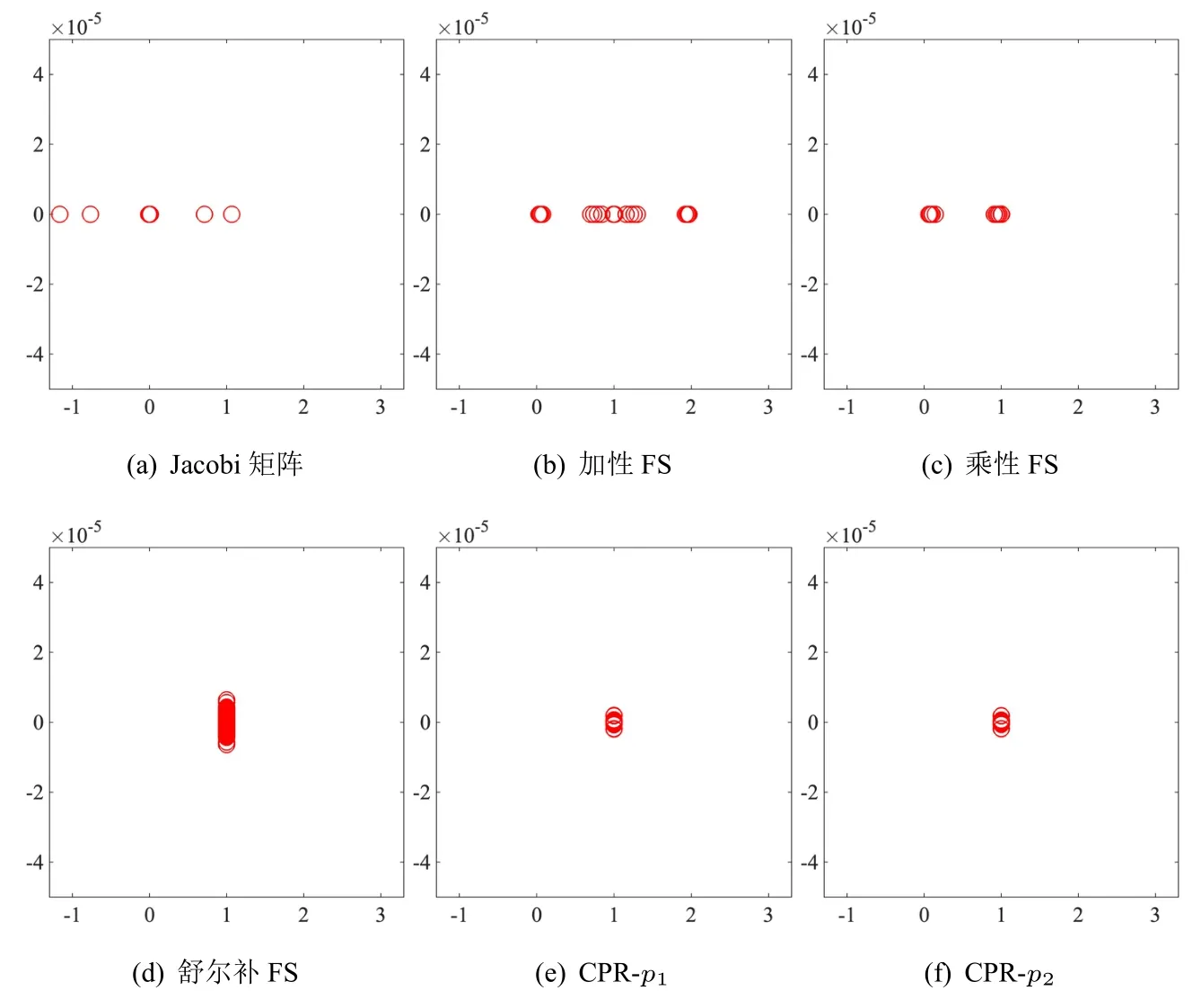
图4 算例二中Jacobi 矩阵和预处理矩阵的特征值分布图

4.3 算例三:SPE10 基准算例

算例三采用SPE10 基准算例(SPE10)[24]来测试三维裂缝型油藏模拟问题.由于渗透率和孔隙度的高度非均质性,该测试算例是油藏模拟中一个具有挑战性的基准问题.如图5所示,基质的渗透率在垂直方向的变化从6.65×10-4md 到2×104md 不等,其变化速度快于水平方向,基质孔隙度不再是一个常数,其范围为0 到0.5.实验中裂缝渗透率值比基质处大400 倍,裂缝孔隙度比基质小30 倍,基质和裂缝中的初始压力随深度变化,设定为10.0Mpa 到10.4Mpa.井底压力为p=3.45Mpa.在数值试验中采用60×220×85 网格对油藏区域1200ft×2200ft×170ft 进行模拟,从区域左侧注入流量,从右侧产出.

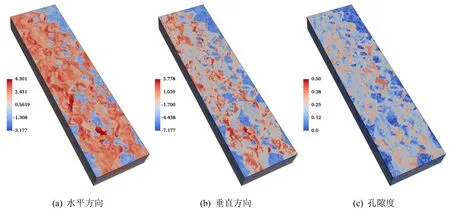
图5 算例三中SPE10 基质渗透率对数分布图和孔隙度分布图

首先测试当时间步长∆t改变时,所提出的不同FS 预条件子的性能,测试结果见表5.在测试中,模拟时间为T=1 天,式(3.3)中的线性停止条件为ηr=10-8和ηa=10-5,式(3.4)中的非线性停止条件为εr=10-10和εa=10-6.表5中的结果表明,采用不同FS 预条件子在几种不同时间步长的迭代过程都是收敛的,且是无条件稳定的;在计算时间方面,CPR 预条件子的性能优于其他FS预条件子,并且随着时间步长∆t的减小,非线性和线性迭代的平均次数变小,而总计算时间增加,这与全隐式方法在各种应用中的结果一致.

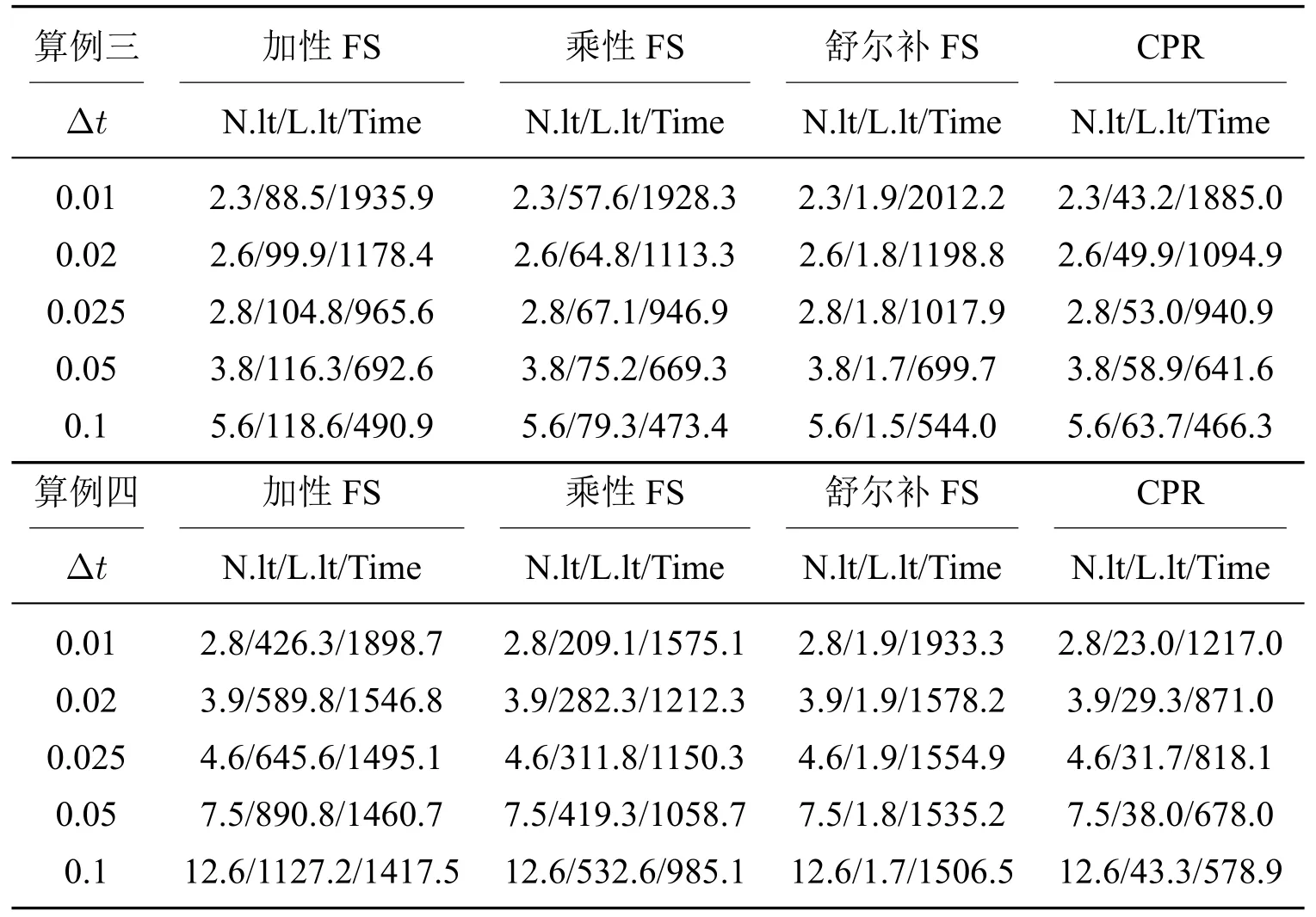
表5 不同时间步长对FS 预条件子性能的影响

4.4 算例四:随机渗透率

在算例四中,使用开源工具箱MRST 生成了网格大小为128×128×128 的随机非均匀渗透率.如图6所示,在基质中,随机渗透率取对数后的分布范围为[0.59,4.1],裂缝渗透率值比基质处大400 倍,基质中的孔隙度为0.05,裂缝中的孔隙度为0.001.在数值试验中对油藏区域[0,100]3进行模拟,从区域左侧注入流量,从右侧产出.试验固定模拟时间为T=1 天,数值结果见表5.从表中可以看出不同FS 预条件子在几种不同时间步长的迭代过程都是收敛的.

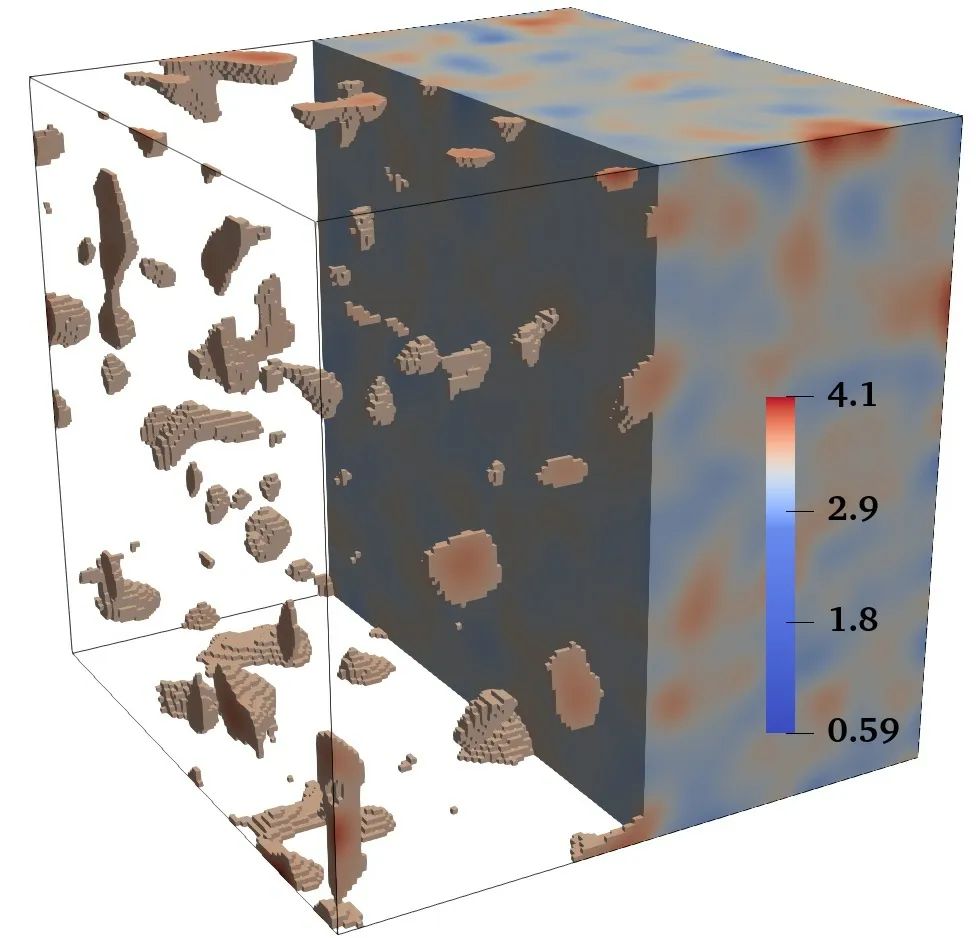
图6 算例四中随机渗透率对数分布图

4.5 并行测试

本小节测试所提出的并行求解器在将Newton-Krylov 算法与一水平或两水平FS 预条件子相结合时的强可扩展性和弱可扩展性.在两水平FS 预条件子中,粗细网格比固定为4,粗网格上的线性系统采用一水平RAS 预条件子的GMRES 方法求解,求解器绝对误差为0.2.可扩展性的衡量指标是Speedup=T1/T2,其中T1和T2分别是使用Np,1和Np,2个处理器(Np,1≤Np,2)时,算法的计算时间.在进行强可扩展性的测试时,将时间步长固定为∆t=0.1 天,网格设置为256×256×256,处理器的数量从128 个依次增加到2048 个,对算例一的前五个时间步长的情形进行模拟.表6为强可扩展性测试的非线性和线性迭代的次数以及在处理器数量下的计算时间,结果表明算法的总计算时间随着处理器数量的增加而减少.在弱可扩展测试中,网格规模从128×128×128(处理器数量Np=128)增大到256×256×256(处理器数量Np=1024),测试结果见表7.结果表明,采用两水平FS 预条件子的Newton–Krylov 求解器具有较好的并行性能,在线性迭代和计算时间方面均优于一水平FS 预条件子.

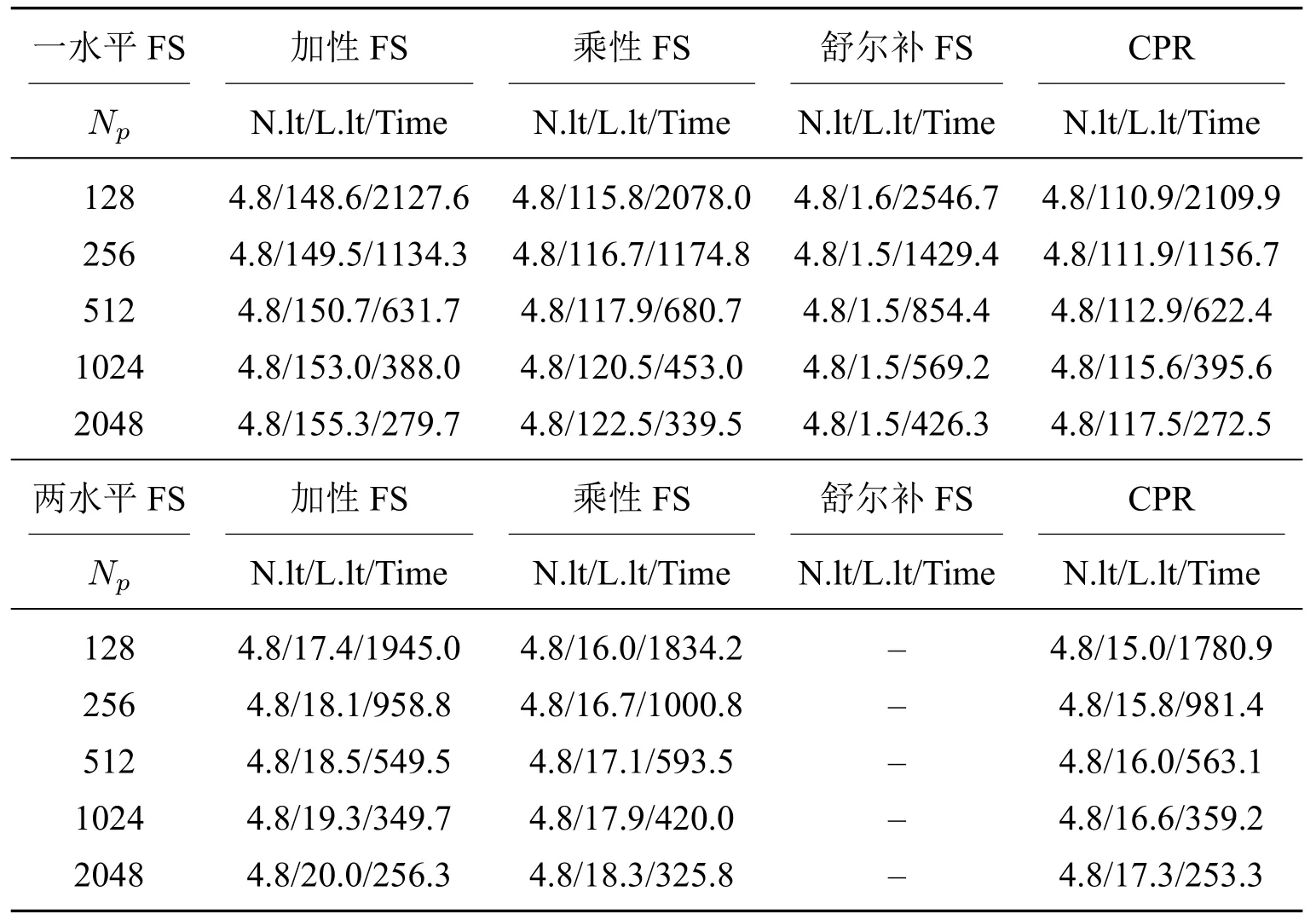
表6 算例一的强可扩展性(“–”表示未测试)

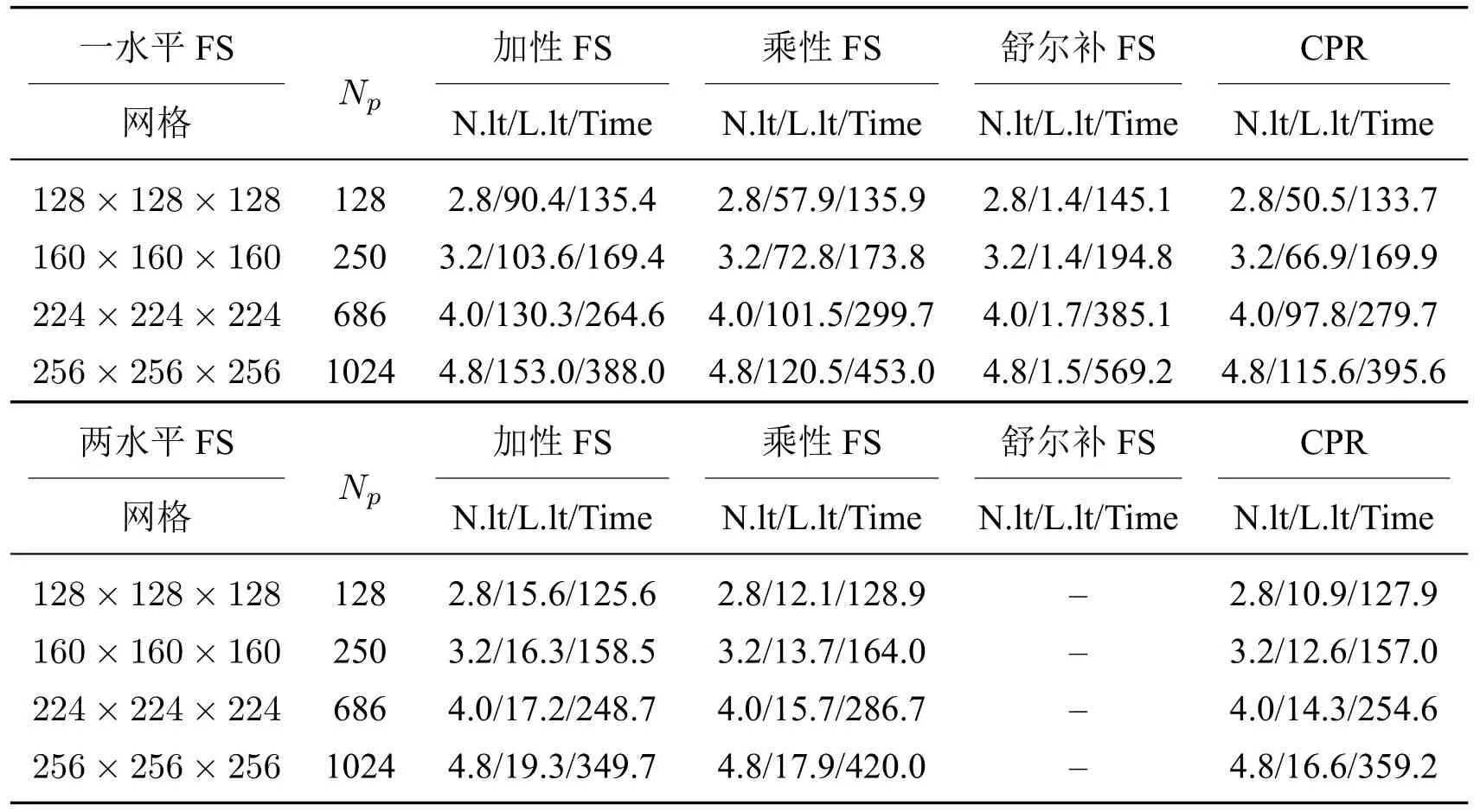
表7 算例一的弱可扩展性(“–”表示未测试)

同样,研究算例二的一水平和两水平FS 预条件子的强、弱可扩展性.表8为强可扩展性测试结果.测试中使用256×256×128 的网格进行模拟,处理器的数量从64 个增加到2048 个,比较非线性和线性迭代的数量以及相对应处理器数量的计算时间.表9为弱扩展性方面的并行性能结果.模拟从使用256 个处理器在256×256×128 的网格上计算开始,以1372 个处理器在448×448×2246网格上计算结束.结果表明,两水平的FS 预条件子在线性迭代和计算时间方面优于一水平FS 方法.随着处理器数量的增加,算法表现出良好的强、弱扩展性,CPR 预条件子优于加性FS 和乘性FS 预条件子.

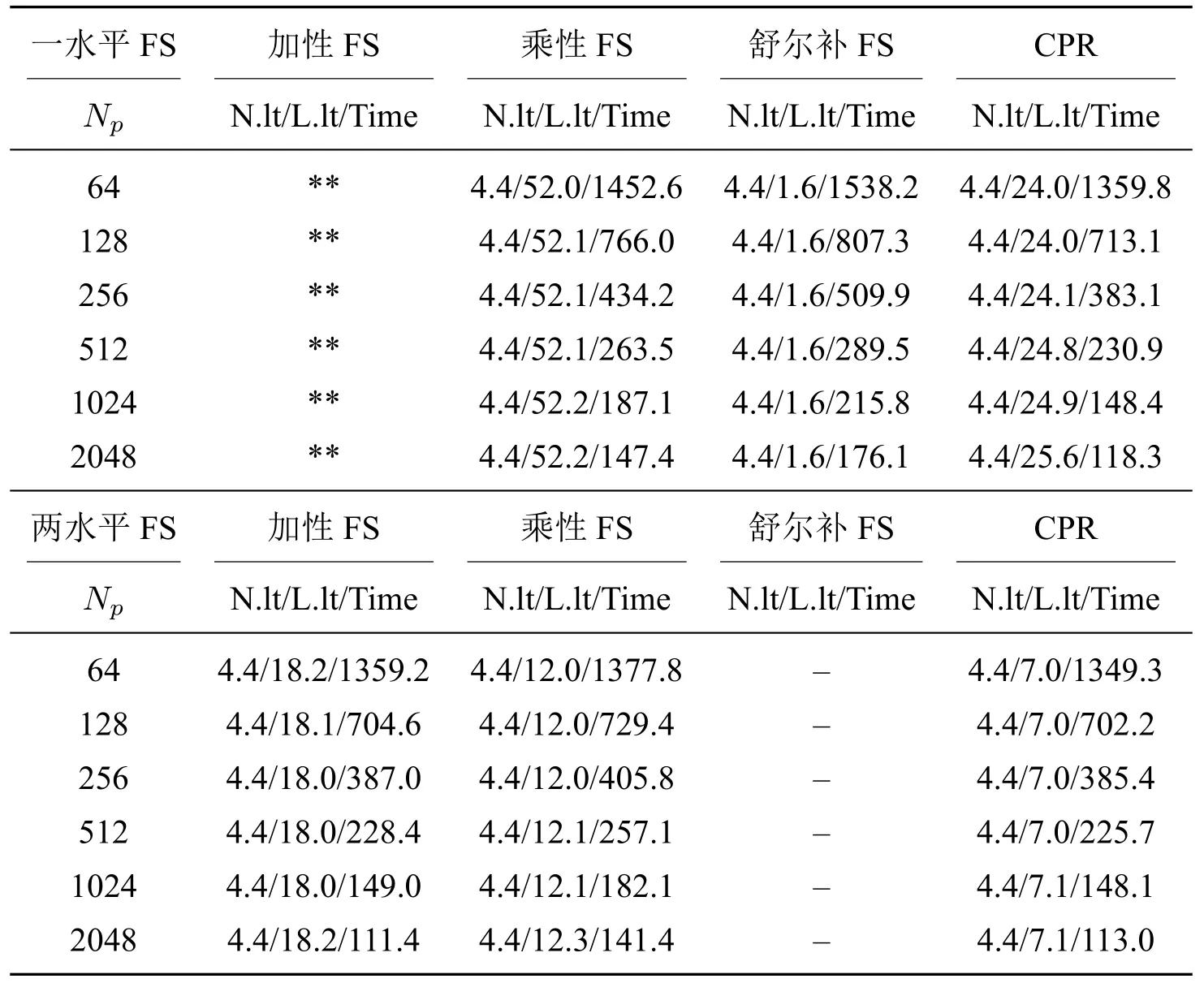
表8 算例二的强可扩展性(“**”表示算法不收敛,“–”表示未测试)

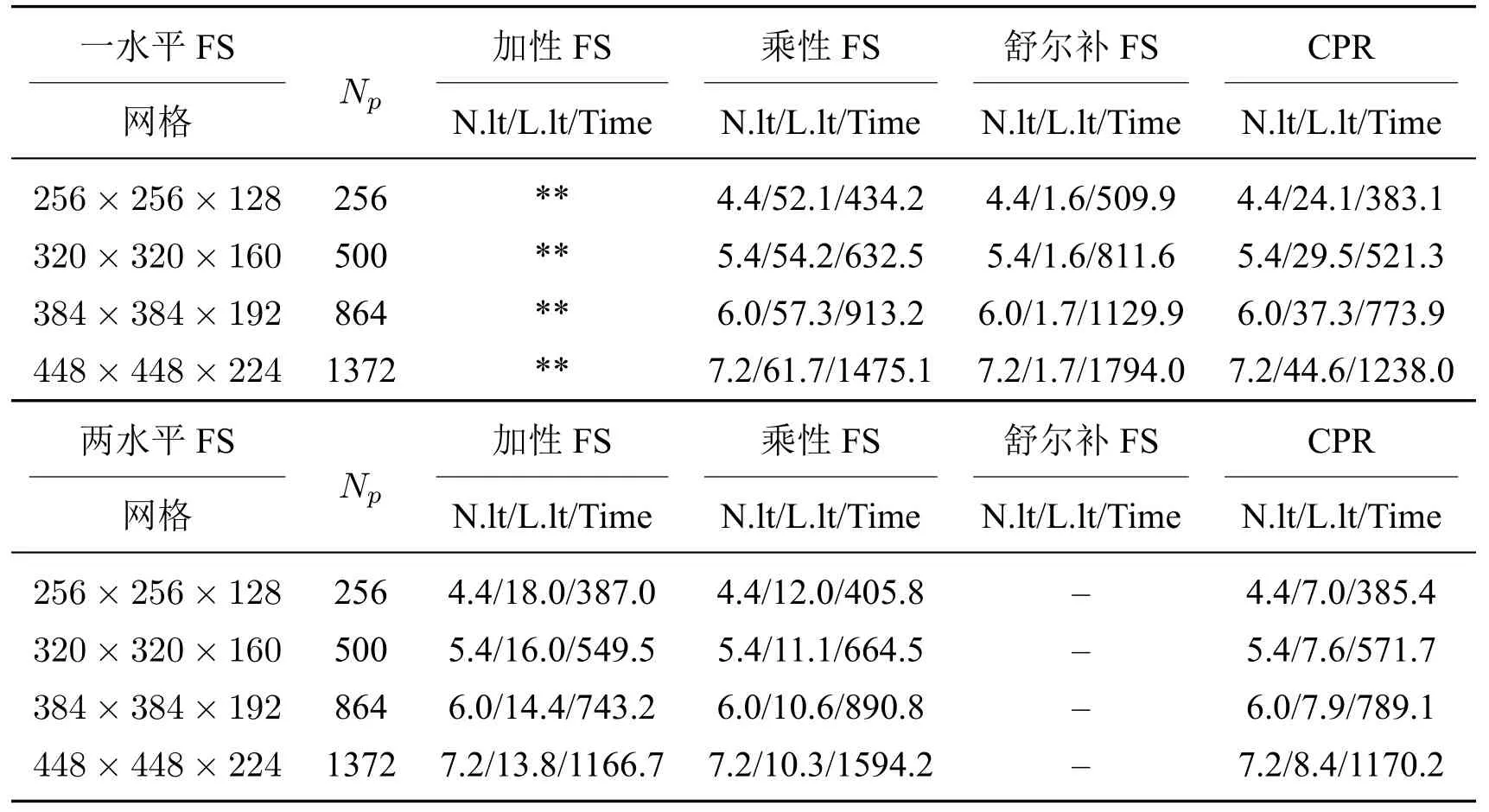
表9 算例二的弱可扩展性(“**”表示算法不收敛,“–”表示未测试)

5 结论

本文研究用于裂缝型多孔介质非定常流动问题的场分裂预条件子.在区域分解框架下考虑几种不同类型的场分裂预条件子,包括加性FS 预条件子、乘性FS 预条件子、舒尔补FS 预条件子和约束压力残差(CPR)预条件子.其中相应的子系统采用限制加性Schwarz(RAS)算法进行近似求解,RAS 的每个子块通过LU 或ILU 分解得到.为了提高一水平FS 预条件子的计算效率和并行性能,在区域分解和多重网格方法的基础上引入粗网格,设计两水平FS 预条件子.最后在超级计算机上计算几个基准案例,得到具有良好鲁棒性和并行可扩展性的精确数值解.在对流动问题进行实验后,发现两水平的CPR 预条件子在线性迭代和计算时间方面对所研究的问题特别有效.本文所提出的多水平场分裂预条件子可以推广到更复杂的流动问题.