系统生物学中的随机微分方程数值仿真算法
2024-01-23牛原玲陈琳陈洛南
牛原玲 陈琳 陈洛南
(1.中南大学数学与统计学院,长沙,410083;2.江西财经大学统计与数据科学学院,南昌,330013;3.中国科学院系统生物学重点实验室,分子细胞科学卓越创新中心(上海生物化学与细胞生物学研究所),上海,200031)
1 引言
随机微分方程(stochastic differential equation)常常用来描述一些自然社会现象中事物的发展规律,由于考虑了随机因素的干扰,它往往能比确定性的微分方程更为准确地刻画变量随时间的演化规律.随机微分方程的本质是随机积分方程,根据所用随机积分的不同,主要分为Itô 型和Stratnovich 型,两种类型的随机微分方程是可以相互转换的.本文我们只关注如下的Itô 型随机微分方程:
其中t∈[0,∞),X(0)=X0,W(t)=(W1(t),W2(t),···,Wd(t))T是d维维纳过程,又称为d维布朗运动.f:R+×Rn→Rn和g:R+×Rn→Rn×d分别称为漂移项系数和扩散项系数,它们均为[0,∞)上的Borel 可测函数.
如果随机扰动出现在微分方程的系数中,如
其中ηt为一个随机过程或者随机变量,这样的方程通常叫做带有随机输入的微分方程(random ordinary differential equation).本文不涉及此类微分方程的数值仿真.
作为一个重要的建模工具,随机微分方程已经在生物、经济、控制等领域得到广泛的应用.但是对大部分随机微分方程而言,一般不能得到其真解.有些随机微分方程的真解虽然可以得到,但由于形式过于复杂,实际应用中不太方便处理.因此,研究随机微分方程的数值算法就显得尤为重要.确定性微分方程的数值算法是一个已经得到长足发展的领域[1–4].近几十年来,国内外对随机微分方程数值计算的研究也取得了快速的发展,参见[5–20].常用的求解随机微分方程的数值方法有Euler-Maruyama 方法、Milstein 方法和Runge-Kutta 方法等.收敛性是数值方法的一个重要评价指标.要求数值方法在一定意义下是收敛的,并且希望其具有较高的收敛阶以提高仿真效率.与确定性的情形不同,随机微分方程数值方法的收敛性有多种定义,其中人们最为关注的分别是强收敛性和弱收敛性.强收敛性要求数值近似的轨道充分接近真实轨道,而弱收敛性关注的则是解过程在矩意义下的收敛性.本文主要涉及前者.此外,我们还希望数值方法能够保持原系统的一些重要特征,比如保区域,保结构等.
本文主要回顾系统生物学中的随机微分方程模型及相关的数值仿真算法.这些随机微分方程一般具有高维、高度非线性、真解位于某个特定的区域等特点,因此对它们的数值模拟需要做专门的研究.鉴于篇幅有限,我们仅从生物化学(生化)反应系统、生态系统、传染病模型、群体遗传学模型以及细胞分化模型的数值仿真来加以阐述.
需要说明的是,目前成熟的商业软件和开源软件中也存在一些可以用于数值求解随机微分方程的软件包:如MATLAB 中的“SDETools”和“SDELab”及R 中的“sde”和“yuima”.其中“SDETools”主要采用的数值格式为Euler–Maruyama 格式和Milstein 格式(要求随机微分方程具有对角噪声);“SDELab”则主要采用θ-Maruyama 和Milstein 格式(不要求随机微分方程具有对角噪声);“sde”仅能数值求解一维的随机微分方程,主要采用的数值格式为Euler–Maruyama 格式,Milstein 格式和Predictor-Corrector 格式;“yuima”可以数值求解多维的随机微分方程(可以是分数阶噪声驱动,也可以存在Levy 跳),采用的数值格式为Euler–Maruyama 格式.这些软件包中采用的数值格式均较为简单,应用于本文提到的这些复杂模型时效果往往不太理想.
2 生化反应系统的数值仿真
细胞中发生的大多数生化反应本质上是随机的.由于传统实验成本昂贵,生化反应系统的随机模拟近年来受到越来越多的关注.假设有一个搅拌良好的生化反应系统,包含N种分子S1,S2,···,SN,这些分子通过多个反应通道在定容恒温的环境下发生反应.用xi(t)(i=1,···,N)表示t时刻Si的数量,则该系统的状态可用向量X=(x1(t),x2(t),···,xN(t))T来表示.用矩阵v表示化学计量矩阵,其元素vij表示第j个反应Rj导致分子Si数量的变化.
2.1 化学主方程模型
化学主方程(Chemical master equation,简记为CME)描述了生化反应系统在不同时间点处于每种状态的概率:
其中X(t)是状态变量,aj(X(t))是倾向函数,aj(X(t))dt表示在下一个小时间段[t,t+dt)第j个反应Rj发生的概率.
化学主方程似乎是发现随机系统时间演化规律的理想方法,它可以返回系统的概率密度函数.然而,化学主方程只有在非常简单的情况下可以求出真解.也就是说,在大多数情况下,需要借助数值方法来对其进行数值模拟.此外,由于必须在每个时间点对每个可能的状态进行评估,并且状态的数量可以呈指数增长,因此计算量非常大,这使得化学主方程模型最初只能有效地用于短期模拟小规模或者简单系统.近年来,虽然化学主方程的数值求解方法取得了长足的进步[21,22,23],但当分子数和倾向函数太大以致于无法使用化学主方程计算时,必须使用新的数值模拟方法,如Gillespie型算法.
2.2 离散状态马尔可夫链模型
随机模拟算法(stochastic simulation algorithm,简记为SSA)由Gillespie 于1977 年提出[24],该方法可以精确模拟化学主方程给出的完整分布中的各条路径,是一种离散状态马尔可夫链方法.由无限多个SSA 模拟建立的概率密度函数将与化学主方程给出的系统真实分布相同.无限次模拟显然是无法达到的,不过适度多的重复次数可以获得令人满意的近似概率密度函数.尽管近年来Gillespie 型方法取得了不小的进展[25–30],但这些算法针对复杂的生化反应系统的计算成本仍然会非常高,尤其是在反应速率和分子数范围很广的情况下.
2.3 郎之万方程模型
在描述生化反应系统时,化学主方程在零分子数时有一个自然边界条件.Fokker-Planck 方程是对化学主方程的近似[31],近似的过程中可能丢失了一些信息,此时,人们需要给Fokker-Planck方程加上合适的边界条件,如Neumann 边界条件[32],反射边界条件[33],以更好地描述生化反应过程.利用Feynman-Kac 公式,某些偏微分方程的解可以用对应的随机微分方程的解来表示.与Fokker-Planck 方程数学上等价的随机微分方程叫做郎之万方程.该模型是离散状态马尔可夫链方法的一种有吸引力的替代方法,因为它可以显著提高计算速度.然而,随机微分方程模型的解可能会变成负数,甚至是虚数.显然,负数甚至是虚数作为分子的数目是不合理的.此时,人们在做数值模拟时通常的做法是,当近似值变为负值时,将其设置为0,或者对维纳增量重新采样,直到数值解为非负值.但这些措施会给数值解带来偏差.文献[34]探索了一种修改化学郎之万方程噪声项的方法,以使变量保持非负.他们只允许物种参与的反应步骤具有随机性.但是,文献[34]在去掉乘积噪声项后得到的改进的保持非负性的郎之万方程不能保证协方差矩阵的匹配条件.文献[35]研究了漂移项和扩散项均为隐式的可保非负性的Milstein 方法,用于数值求解化学郎之万方程.该格式在牛顿迭代中施加了取值非负的约束,计算过程中需要删除因反应物耗尽而停止的反应通道Rj,即删除化学计量矩阵v的第j列vj和相应的倾向函数aj,直到反应物浓度再次升高,再将删除的反应通道Rj恢复,同时修改化学计量矩阵和倾向函数.这些措施使得算法的“保非负性”得以实现.该方案始终满足协方差矩阵匹配条件.但是因为全隐式方法需要额外的计算,并且计算过程中需要实时修改化学计量矩阵和倾向函数,所以计算成本可能非常高.文献[36]表明,通过将郎之万方程的定义域扩展到复空间,得到复数域上的郎之万方程,该方程得到的反应物的平均浓度落在实数域.但是此时分子数是复数,在生物学上不合理.
当使用化学郎之万方程通过连续过程近似化学主方程描述的离散过程时,目前尚不太清楚边界条件的行为.文献[37]中,作者通过将边界条件纳入随机微分方程,得到了确保随机微分方程模型的生物学上合理的解决方案.由此产生的模型称为带反射边界的随机微分方程模型.此类方程之前曾用于模拟人类代谢过程[38],离子通道动力学[39]等.
带边界条件的生化反应模型如下:
其中W(t)为维纳过程.ξ(t)有局部的有界变差,ξ(0)=0.|ξ|(t)非负递增连续并且满足(2.3)–(2.4)式.如果X(s)∈∂D,那么,n(s)∈N(X(s)),其中N(y)表示当y在边界上时,指向区域内部的单位向量.(2.3)式表明当且仅当X(t)∈∂D时,|ξ|(t)会增长.当X(t)不落在边界上时,dξ(t)消失,此时带反射边界的随机微分方程(2.2)退化为普通的随机微分方程
由(2.2)–(2.4)建立的带反射边界的随机微分方程模型似乎是建立生化反应系统模型的理想方法,它的解具有生物意义.但是在大多数情况下,此类随机微分方程并没有解析解,因此数值近似是获得解并研究其性质的重要途径.这里的定义域D是凸的,因此大多数现有的数值算法可以应用于此处提出的带反射边界的随机微分方程模型的数值模拟.投影法是Euler-Maruyama 方法的简单扩展,可用于求解带反射边界的随机微分方程:如果Euler-Maruyama 方法获得的数值解位于D的闭包之外,则将下一时间步的解设置为该点在闭包D上的投影,否则该步的数值逼近等于Euler-Maruyama 方法得到的数值解.数值实验表明,利用(2.2)–(2.4)确定的带反射边界的随机微分方程模型得到的数值模拟结果与SSA 得到的数值模拟结果非常接近,但是时间成本则大大降低.
Goldbeter-Koshland 开关是由两种具有相反作用的酶E1 和E2 促进的共价修饰生化反应系统,它由以下6 个反应组成:
取初始状态(110,100,30,30,100,30)T及参数k1=0.05,k2=0.1,k3=0.1,k4=0.01,k5=0.1,k6=0.1,文献[37]对上述生化反应系统进行了数值模拟,结果如图1所示.由图1可以看到,带反射边界的随机微分方程模型与SSA 得到的数值模拟结果非常接近.而SSA 所花的CPU 时间为51h55min40s,带反射边界的随机微分方程的数值模拟所花的CPU 时间则为3h37min47s,可见后者的数值模拟效率大为提高.

图1 SSA 与带反射边界的随机微分方程对Goldbeter-Koshland 开关数值模拟的均值和方差(实线:SSA,虚线:带反射边界的随机微分方程)[37]
这一工作的主要贡献在于提供了一种计算高效的方法来模拟生化反应系统.该方法不仅可以保持离散状态马尔可夫模型的随机行为,并且可以保证真解及数值解都有生物意义,从而使得针对大规模生化反应系统的数值仿真成为可能.值得注意的是,即使带反射边界的随机微分方程模型在许多情况下表现得足够好,但它并不太适合所有反应通道的倾向函数都非常小的生化反应系统.这种情况下需要用到2.2 节提到的Gillespie 型算法.
3 生态系统的数值仿真
生态数学中,通过“变化率=输入-输出”这样的思路可以建立起常微分方程模型,如在Logistic 模型基础上得到的Lotka-Volterra 模型.近年来,一些学者对Lotka-Volterra 模型引入了随机扰动,将其转化为随机Lotka-Volterra 模型,其中随机性通常是由环境的不可预测性和对生态系统的不完全认知引起的.随机Lotka-Volterra 模型能够更精确地描述客观现象.随机Lotka-Volterra竞争模型,随机Lotka-Volterra 捕食模型和随机Lotka-Volterra 合作模型是其中最为典型的代表.
3.1 随机Lotka-Volterra 竞争模型
Mao 在其专著[40]中研究了如下的随机Lotka-Volterra 竞争模型:
其中x(t)=(x1(t),x2(t),···,xd(t))T是生态系统中d个相互作用的种群在t时刻的状态,b=(b1,···,bd)T∈Rd,σ=(σ1,···,σd)T∈Rd,A=(aij)d×d∈Rd×d为系统的参数.文献[40]指出,当矩阵A的元素均为非负,即aij≥0(1≤i,j≤d)时,对任意的初始值x(0)∈,方程(3.1)有唯一的强解x(t),并且满足x(t)∈,其中={(x1,···,xd)T∈Rd:xi≥0,1≤i≤d}.作者还研究了带延迟的随机Lotka-Volterra 竞争模型真解的性质.
诸如方程(3.1)这样的随机微分方程,具有以下特点:高度非线性,正解,多维.这些特点给数值模拟带来了很大的挑战.文献[41]针对方程(3.1),在截断算法的基础上,引入非负投影来确保算法的非负性,给出了一种保正截断Euler-Maruyama 方法.作者证明了该数值算法是保正的和强收敛的.数值算例显示,该方法具有1/2 阶的强收敛阶,但作者并没有给出相关的理论证明.
文献[42]则在矩阵A的所有元素非负且对角线元素为正的条件下,针对方程(3.1)提出了一种线性隐式Milstein 方法.该方法不仅能保正,并且能保证解的长时间有界性.数值实验表明,该方法具有1 阶的强收敛阶,但作者理论证明方法的强收敛阶仅为1/2.
文献[43]借助对数变换将方程(3.1)转换成带有加性噪声的随机微分方程,并对转换后的方程应用显式Euler-Maruyama 算法进行数值求解.作者通过对数变换使得数值算法可以保持非负性,并利用随机摄动理论证明了算法的1/2 阶强收敛性.
3.2 随机Lotka-Volterra 捕食模型
除了3.1 节中介绍的竞争模型,捕食模型也是生态学中一种重要的模型.文献[44]研究了这类模型解的存在唯一性.文献[45,46]分析了随机Lotka-Volterra 捕食模型的长时间行为.此外,文献[47]研究了带时滞的随机Lotka-Volterra 捕食模型的正解的存在性.
文献[48]考虑了如下的一类随机Lotka-Volterra 捕食模型
其中X(t)=(x1(t),···,xd(t))T和Y(t)=(y1(t),···,yd(t))T分别是t时刻被捕食者和捕食者的数目,η(1)=表示在没有食物的情况下捕食者的自然死亡率,而η(2)=表示没有捕食者时被捕食者的自然增长率.
作者证明了模型(3.2)具有唯一的正解,并且具有随机辛结构,故可以被看作是一个随机哈密尔顿系统.同时,作者提出了一种随机Runge-Kutta 方法,并且证明了该数值格式可以保持数值解为正和原系统的随机辛结构.事实上,作者是通过对数变换来实现保正的.此外,作者还证明了该数值格式是1 阶收敛的.
3.3 随机Lotka-Volterra 合作模型
Lotka-Volterra 合作模型描述了自然界以及人类社会中物种或群体之间的互惠互利关系,如蜜蜂和花.文献[49] 将白噪声引入到一类时滞Lotka-Volterra 模型的内禀增长率中,建立了持续性的充分条件,并获得了平稳分布的存在唯一性.文献[50] 研究了食物有限情况下的随机Lotka-Volterra 合作模型,并给出了持续和灭绝的充分条件.文献[51]考虑了如下带有年龄结构的随机Lotka-Volterra 合作模型:
其中X(t,a) 和Y(t,a) 分别是两个物种在t时刻、a年龄时的密度,γ1(a) 和γ2(a) 分别是物种的内禀增长率,α11(a)和α22(a)表示种内竞争率,α12(a)和α21(a)表示种间合作率,γ1(a),γ2(a),α11(a),α22(a),α12(a)和α21(a)均为正数.
与前面提到的其他模型不同,带年龄结构的随机Lotka-Volterra 合作模型(3.3)是一个随机偏微分方程.事实上,考虑到年龄结构的种群模型都是偏微分方程.文献[51]证明了方程(3.3)全局解的存在唯一性,并且分析了Euler-Maruyama 方法用于方程(3.3)的数值求解时的收敛率.但[51]并没有证明数值解的保正性.
值得注意的是,这里谈到的Lotka-Volterra 模型不仅可用于描述种群动力学,还可用于物理学和经济学等方面的建模.
4 随机传染病模型的数值仿真
近年来,世界经济和人类健康均受到新型冠状病毒的影响,该病毒已经严重影响了人们正常的生产生活.历史上也出现过许多类似的传染病,例如黑死病,“非典”等.数理流行病模型已经成为了解疫情,掌握疫情变化的重要工具.数学家们建立了很多著名的传染病数学模型,例如SIS,SIQS,SIR,SEIR 模型等.
事实上,在现实生活中,任何一个系统都会受到或多或少的随机干扰.正因如此,对具有随机扰动的传染病模型的研究是非常重要且是有意义的.据此我们可以得到随机版本的SIS,SIQS,SIR,SEIR 模型等.这些模型都是具有非线性系数的随机微分方程,它们的解析解通常很难求出.因此需要使用计算机来对其进行数值模拟,从而达到对传染病模型的研究.系数不满足单边Lipschitz 条件,数值解需要保持真解位于特定区域的性质,这是对随机传染病模型进行数值模拟的两大难点.
4.1 随机SIR 模型
1927 年数学家Kermack 与McKendrick 在研究传染病时提出了SIR 仓室模型[52].此模型是最为经典的传染病数学模型,当时该模型的提出主要针对欧洲出现的黑死病.模型将人群分为3 类,分别为易感者(S 类)、感染者(I 类)和康复者(R 类).该模型适用于治愈后康复者具有很强的免疫力,不会再次被感染的传染病,如水痘等.此外,该模型还适用于一些致死性的传染病,因为死亡的病人也可以归入“康复者(R)”.这里的“康复”可以理解为是退出了系统.
文献[53]将所提出的数值算法成功运用于如下的随机SIR 模型:
其中参数Λ,β,µ和γ为正常数,Λ 表示易感个体自然出生率,µ表示每个个体类别自然死亡率,β为疾病接触率,γ表示受感染个体的恢复率.在初值假设S(0)+I(0)+R(0)=Λ/µ下,模型(4.1)满足群体总人口不变,即在任意时刻t都有S(t)+I(t)+R(t)=Λ/µ.文献[53]提出了一种增量驯服的Euler 算法,并得到了模型(4.1)数值近似的强收敛性.
文献[54]针对模型(4.1)构造了一种维纳截断的线性隐式算法,在确保数值近似取值非负的基础上,得到了算法是强1/2 阶收敛的,并讨论了算法的数值动力学行为.
文献[55]则在另一类随机扰动下研究了如下随机SIR 模型:
其中受感染个体以ε的速率变得易感并转移到易感类别,其他参数与模型(4.1)一致.但由于模型中康复者也受到随机因素影响,模型(4.2)的人口总数带有随机性.针对模型(4.2),作者提出了一种基于勒让德多项式的勒让德谱配置方法来求解.
4.2 随机SIS 模型
在随机SIR 模型的数值分析中,如何得到算法的收敛阶仍然有一些困难.但对相对简单的随机SIS 传染病模型,在其数值近似方面有着丰富的研究成果.
在文献[56]中,作者考虑了如下的随机SIS 模型:
其中S(t),I(t)表示t时刻的易感者和感染者数目,N是疾病在其中传播的人口总数,µ是人均死亡率,1/γ为平均感染期,β是疾病传播系数.SIS 模型可以看作SIR 模型的特殊情形,适用于感染后不产生永久免疫力的疾病建模,如一些性传播疾病和细菌性疾病.对于这些疾病,个体起初易感,在某个阶段感染该疾病,并在短的感染期后再次易感.文献[56]证明了模型(4.3)具有唯一的全局正解I(t),并建立了I(t)灭绝和持续的条件.
文献[57]提出了一种显式的数值格式,称为Lamperti 平滑截断格式(LST),用于对随机SIS 模型的数值模拟.该方案将Lamperti 型变换(实质上为对数变换)与显式截断方法相结合,所得的数值近似结果保持了原始随机微分方程的解位于特定区域的性质,并且具有1 阶均方收敛阶.这里使用的Lamperti 型变换只能用于一维的随机微分方程,变换后的随机微分方程的系数满足单边Lipschitz 条件.由于(4.3)式中的变量满足S(t)+I(t)=N,所以Lamperti 型变换在这里是可以使用的.此时(4.3)式变为:
当βN-µ-γ=5,β=0.8,σ=0.1,N=10 时,作者给出了用Lamperti 平滑截断格式求解(4.4)式的收敛阶,如图2所示.其中LST 即为这里的Lamperti 平滑截断格式.由图2 可知,该方法具有1 阶收敛阶.虽然LBE,即Lamperti 向后Euler 格式[63],也具有1 阶收敛阶,但由于LBE 是隐式的,需要求解超越方程,所以LST 算法的运行时间明显低于LBE 算法.显然,LST 算法比LBE 算法更有效.
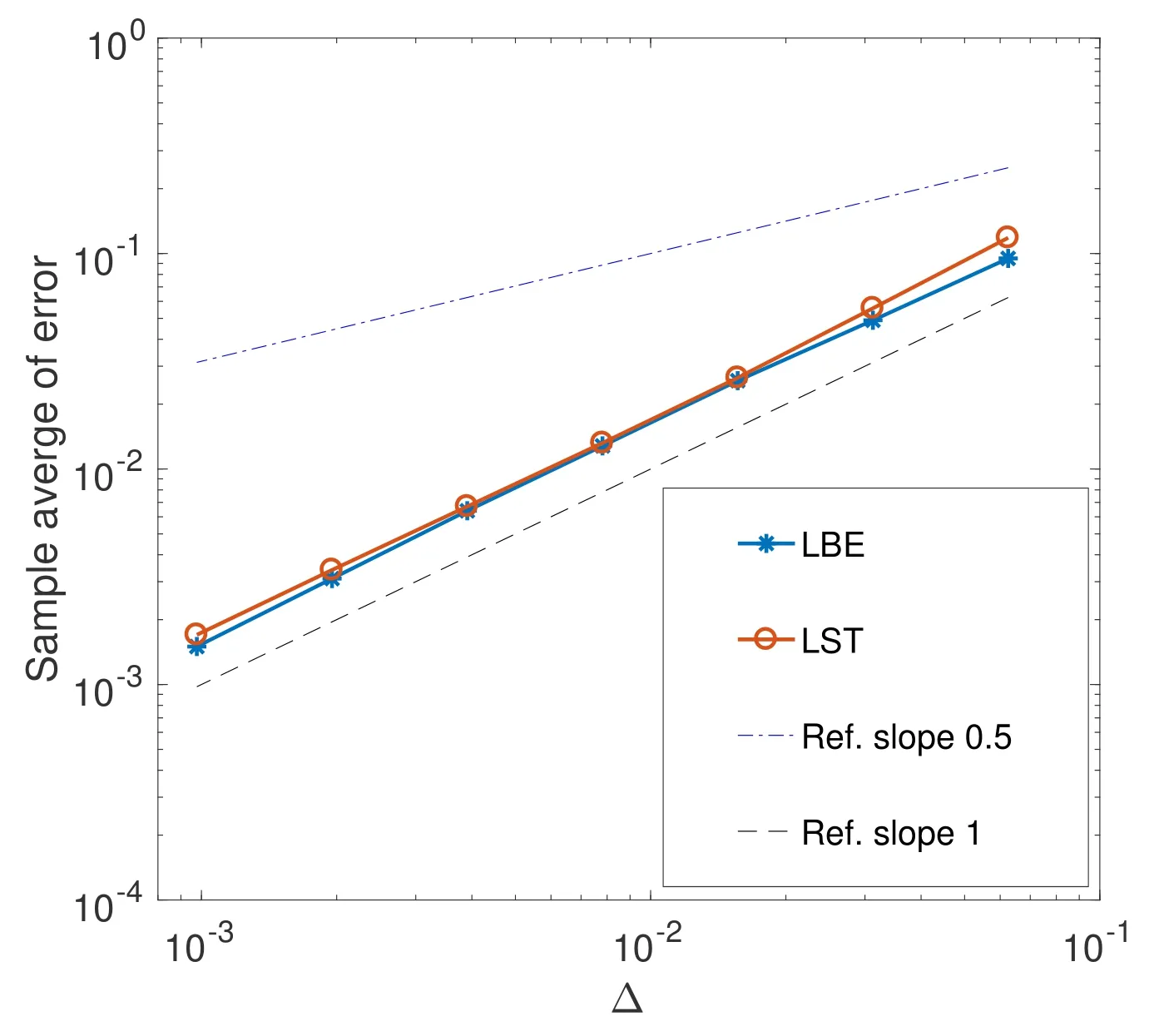
图2 LST 算法求解随机SIS 模型的均方误差[57]
在文献[58]中,作者通过结合对数变换和Euler-Maruyama 方法,为随机SIS 模型构造了一种保正的数值方法,证明了该算法不仅保留了原始随机微分方程的值域,而且在所有p>0 的情况下,在有限时间间隔内具有1 阶Lp收敛阶.
文献[59]考虑了随机SIS 模型的带截断维纳过程的分裂步θ方法,证明了该数值格式具有1/2 阶均方收敛阶,数值解保正且有界.虽然收敛阶比[57]提出的LST 算法要低,但是不需要做Lamperti 型变换,可以直接近似求解原方程.事实上,该方法通过将维纳过程截断来保正,因此无需做变换.
此外,文献[60]构造了一种带有两个随机扰动项的SIS 模型,证明了该模型具有唯一且有界的全局解,分析了模型中感染人群I(t)持续、灭绝的条件.之后文献[61]通过在平方根内取绝对值的方式,针对该模型提出了一种保取值范围的数值算法,并得到了该算法的收敛性,但没有给出算法的收敛阶.
5 群体遗传学模型的数值仿真
群体遗传学中一个非常重要的模型是Wright-Fisher 模型,于20 世纪30 年代由Wright 和Fisher 独立引入,它描述了种群遗传结构中的随机进化.
文献[62]考虑了如下的Wright-Fisher 模型:
其中参数的具体意义见[62].Wright-Fisher 模型最初用于模拟有限群体内的遗传漂移,在文献[62]中被用作心脏和神经细胞内离子通道动力学的模型.该方程的解落在区间[0,1]内,但多数数值方法无法在数值模拟时保证此类取值范围.[62]结合隐式平衡算法和分裂步算法,提出了一种平衡隐式分裂步算法,可使得数值解始终以概率1 保持在[0,1]内,并证明了该方法的强收敛性.数值实验表明,该格式具有强1/2 阶收敛性.将该方法推广到多维情况,数值试验表明该算法仍然具有1/2 阶的强收敛性.取A=1,B=2,C=0.2462,将平衡分裂步算法应用于Wright-Fisher 模型(5.1)的数值实验结果如图3所示.
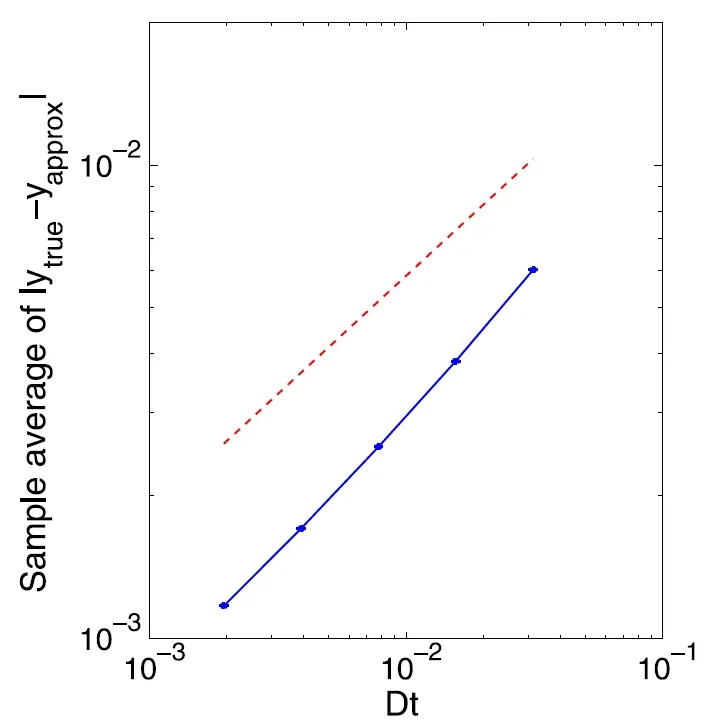
图3 平衡隐式分裂步算法求解Wright-Fisher 模型(5.1)的收敛性.红色虚线是斜率为1/2 的参考线[62]
在文献[63]中,针对这类具有非Lipschitz 漂移或扩散系数且取值在区域D=(l,r)内的标量随机微分方程,作者提出了一种Lamperti-Euler 格式(LBE).首先借助Lamperti 变换x(t)=F(y(t)),使用向后Euler 格式近似变换过程x(t),再用Lamperti 逆变换进行反向变换,得到原始随机微分方程的近似值.该数值格式具有1 阶收敛性,并且可以保持原始随机微分方程的取值在D内.
这里的LBE 格式是较早使用Lamperti 变换实现数值解保正的格式.随机SIS 模型对应的Lamperti 变换是对数变换,而Wright-Fisher 模型对应的则是三角变换.需要注意的是,变换后的隐式数值格式在每一步都需要求解超越方程,计算成本较高.为了克服隐式算法计算成本较大的难点,最近文献[64]在Lamperti 变换的基础上提出一种新的显式倾斜截断算法,不仅得到了算法的强1 阶收敛性,还得到了数值近似的平稳分布收敛性.
6 细胞分化模型的数值仿真
细胞分化过程形成了形态、结构、功能各异的细胞类型,使得生物世界丰富多彩.对基因调控网络的建模对理解细胞的分化至关重要.构建生物系统的表观遗传景观是研究细胞分化的重要工具.
目前主要有以下两种方法可以用来构造势能景观:一种是基于数据的方法,即从实验数据,特别是单细胞RNA 测序(scRNA-seq) 数据中识别细胞类型、分化轨迹和细胞多能性,如文献[65,66,67]等;另一种方法是基于模型的方法,即构建基因调控网络的动力学方程,分析系统的动力学行为,并使用数值模拟构建势能景观,如文献[68,69]等.
在文献[68]中,作者用如下带生灭项的Fokker-Planck 方程作为种群水平上的细胞分化模型:
其中x表示基因表达水平,b(x)表示基因间的相互作用,ε代表噪声的强度,R(x)表示x处的细胞的出生与死亡率,即生灭项.同时,作者用如下的随机微分方程作为单细胞水平的细胞分化模型:
其中Xt(ω)为细胞ω在t时刻的基因表达水平,ρt(ω)代表细胞ω的时变权重.由Itô 公式可知,(6.1),(6.2)两个模型的等价关系可以由下式得到
这里,δ是狄拉克函数,E 表示对所有可能的轨道ω取期望.
在构建势能景观的过程中,针对低维模型,作者使用有限元方法或者有限差分方法直接对种群水平上的细胞分化模型(6.1)进行数值求解直至稳态;针对高维模型,则对单细胞水平的细胞分化模型(6.2)进行平均场近似,然后再根据所获得的稳态概率密度函数及作者提出的势能景观分解理论,得到细胞类型势能景观U(x)和体现细胞干性的多潜能性势能景观V(x):U(x)=-εlogPU(x),V(x)=-εlog (P0(x)/PU(x)),其中PU(x)表示当R(x)给定时,由(6.1)或(6.2)得到的稳态概率密度函数,P0(x)表示当R(x)≡0 时,由(6.1)或(6.2)得到的稳态概率密度函数.
7 结论
随着近年来交叉学科的蓬勃发展,涌现了大量与系统生物学相关的随机微分方程模型.这些模型由于来源于现实世界,有一定的生物背景,通常具有以下一个或者若干个特点:解位于特定区域,高维,系数不满足Lipschitz 条件等.以上这些特点为数值算法的构造及理论分析带来了挑战.常用的数值算法用来做这类模型的数值仿真时要么不收敛,要么不能保持真解的某些性质,如位于特定的区域等.Lamperti 型变换算法,隐式高阶算法或者平衡隐式算法可能是针对这类问题构造数值格式的备选方案.目前已有的保取值域的方法主要包括:投影(文献中也称截断),相关文献有[41]等;对数变换,相关文献有[47,57,58]等;平衡隐式方法,相关文献有[62]等;维纳增量截断,相关文献有[59]等.
对于引言中提到的带有随机输入的微分方程(random ordinary differential equation)的数值模拟,可参考文献[70].系统生物学家通常使用这类方程对生态系统进行建模,如文献[71,72]等.
鉴于篇幅和时间有限,本文所综述的工作难免挂一漏万,敬请读者海涵.
