求解Allen-Cahn 方程的半隐配点格式
2024-01-23童艳蕾姚晓珍林梦渟李怡雯翁智峰
童艳蕾 姚晓珍 林梦渟 李怡雯 翁智峰
(华侨大学数学科学学院,泉州,362021)
1 引言
1.1 研究背景
Allen-Cahn 方程作为描述相场模型最基本的方程之一,可用于模拟二元合金相位分离的过程.此外,Allen-Cahn 方程也常用于描述一定温度和气压下晶体的生长[1]、生物种群之间的竞争和排斥现象[2]、河床的迁移现象[3],平均曲率-流量[4]等问题.
Allen-Cahn 方程是具有如下形式的方程:
其中,ε为界面宽度,∆为拉普拉斯算子,f(u) 为给定的非线性函数,满足f(u)=F′(u),其中F(u)=是一种双阱势函数.
Allen-Cahn 方程的一个重要特征是:它可以被看成能量泛函
的梯度流形式.因此,其能量泛函满足递减关系
由于Allen-Cahn 方程的解析解通常很难得到,因此研究其数值解变得十分重要.学者们对其提出了许多数值解法.比如,Chen 等[5]基于有限差分法求解Allen-Cahn 方程并分析了其数值格式的收敛性; Zhai 等[6]提出了求解三维Allen-Cahn 方程的高阶紧致ADI 方法; Li 等[7]给出了Allen-Cahn 方程的二阶无条件能量稳定的有限元格式;Feng 和Li[8]构造了一种对称内罚间断有限元格式;Weng 和Tang[9]利用算子分裂格式结合谱方法求解Allen-Cahn 方程;Wang 等[10]提出了一种线性能量稳定和保极大值原理的半隐格式求解Allen-Cahn 方程;Li 等[11]构造了Allen-Cahn 方程的降阶修正有限差分格式;Li 和Wang[12]给出了一种修正有限体积元方法求解Allen-Cahn 方程;Hou 和Leng[13]构造了一个稳定的Crank-Nicolson/Adams-Bashforth 格式;Feng 等[14]给出了一个无条件能量稳定的线性二阶有限差分格式.
上述方法都是基于网格剖分的思想求解Allen-Cahn 方程.文献[15]提出一种新型无网格的重心插值配点法,该方法具有计算格式简单、精度高、程序实施方便、节点适应性好等特点,被广泛应用于求解各类微分方程,比如Cahn-Hilliard 方程[16]、Helmholtz 方程[17]、Black-Scholes 方程[18]、Allen-Cahn 方程[19]等.最近,Yi 和Yao[20]利用重心插值配点法求解时间分数阶电报方程并给出了对应的误差估计;Li 和Cheng[21]分析了热传导方程在重心有理插值配点格式下的误差估计.
针对非线性微分方程,Ascher 等[22]提出了一种显隐方法.该方法对方程的非线性项采用显式处理,对线性项做隐式处理,避免了非线性迭代,可以提高计算效率.沈和马[23]提出了一种半隐差分法求解Zakharov 方程;潘[24]给出了Allen-Cahn 方程的一种高阶显隐格式;汤和乔[25]给出了相场方程的一种高效数值算法.
基于前人的工作,本文利用重心插值配点法结合半隐格式求解Allen-Cahn 方程,对方程的空间一维半离散格式和二维全离散格式进行相容性分析,并通过数值算例验证算法的高精度性和数值格式的能量递减物理性质.
1.2 重心Lagrange 插值与Chebyshev 配点法
重心Lagrange 插值设有m+1 个插值节点xj和相对应的一组实数fj,j=0,1,···,m.在次数不超过m的多项式空间中,存在唯一一个多项式p(x),满足p(xj)=fj(j=0,1,···,m).多项式p(x)即为如下的Larange 插值多项式:
其中,Lagrange 插值基函数κj(x)满足性质:
由于Lagrange 插值公式的计算量达到O(n2),且增加新节点时需要重新计算,为了减少重复计算,我们令l(x)=(x-x0)(x-x1)···(x-xm),定义重心权
将插值基函数表示为:
再代入式(1.2),得
由式(1.3),(1.4)可得
再代入式(1.5)可得重心Lagrange 插值公式:
其中
Chebyshev 配点法多项式插值在节点数m较大时,若采用等距节点,其插值是病态的.因此本文将以第二类Chebyshev 节点作为空间方向的插值节点.
在区间[-1,1]上的第二类Chebyshev 节点为:
相应的重心Lagrange 插值的权为:
任意区间[a,b]上的Chebyshev 节点可通过坐标变换y=x(b-a)/2+(a+b)/2 得到.
重心插值的微分矩阵函数p(x)在节点xi处的k阶导数为:
由Lj的定义可得到一阶、二阶重心插值微分矩阵,其元素如下:
由数学归纳法可以得到k阶重心插值微分矩阵,其元素如下:
2 一维Allen-Cahn 方程的空间半离散格式及其相容性
2.1 一维Allen-Cahn 方程的空间半离散格式
考虑一维Allen-Cahn 方程的初边值问题:
式中u(x,t)为未知函数,ε为界面宽度系数,g(x),θ(t),ω(t)为已知函数,且非线性项f(u)=u-u3.
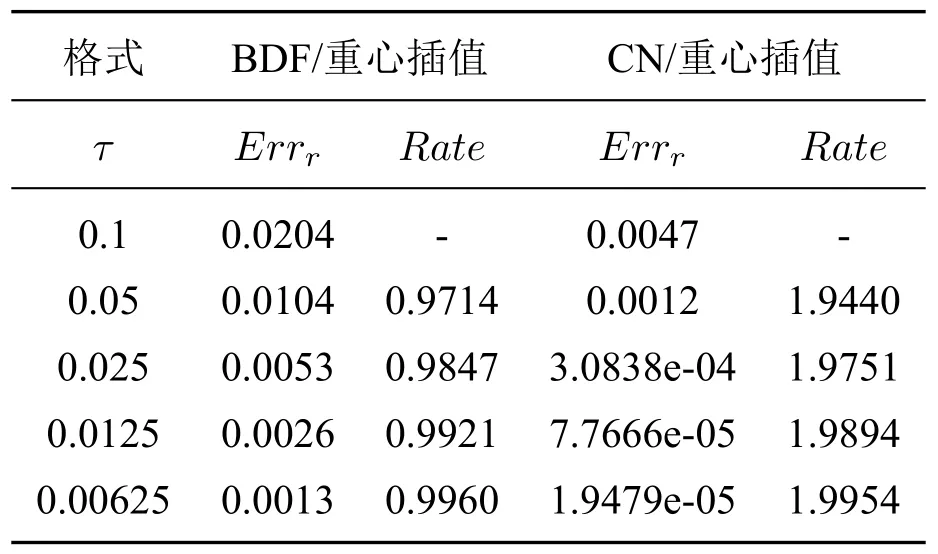
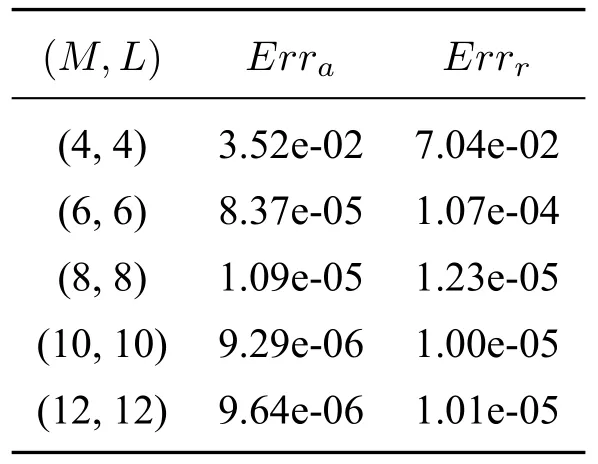
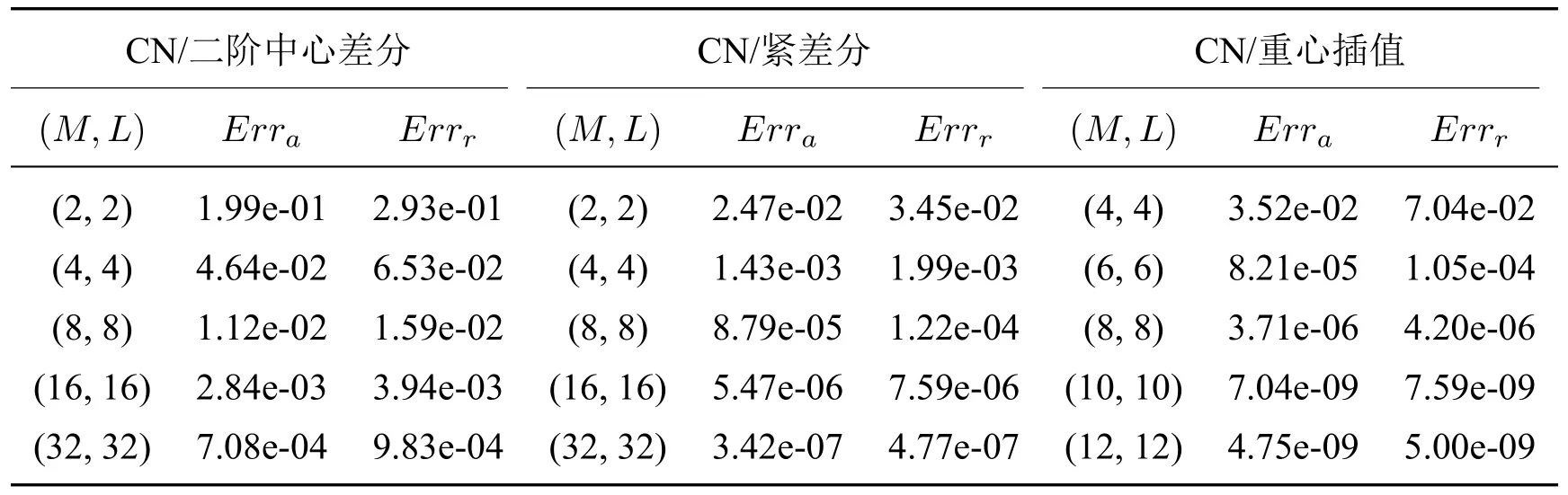
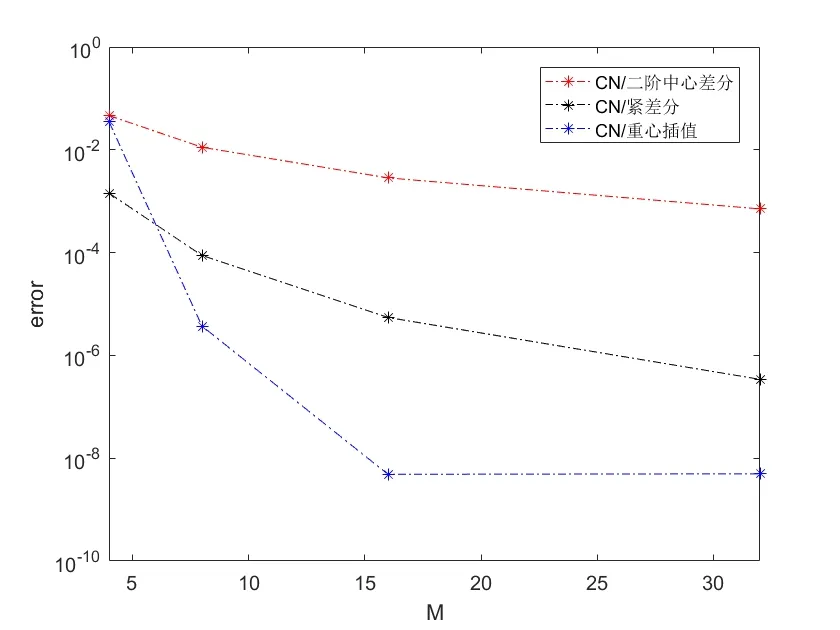
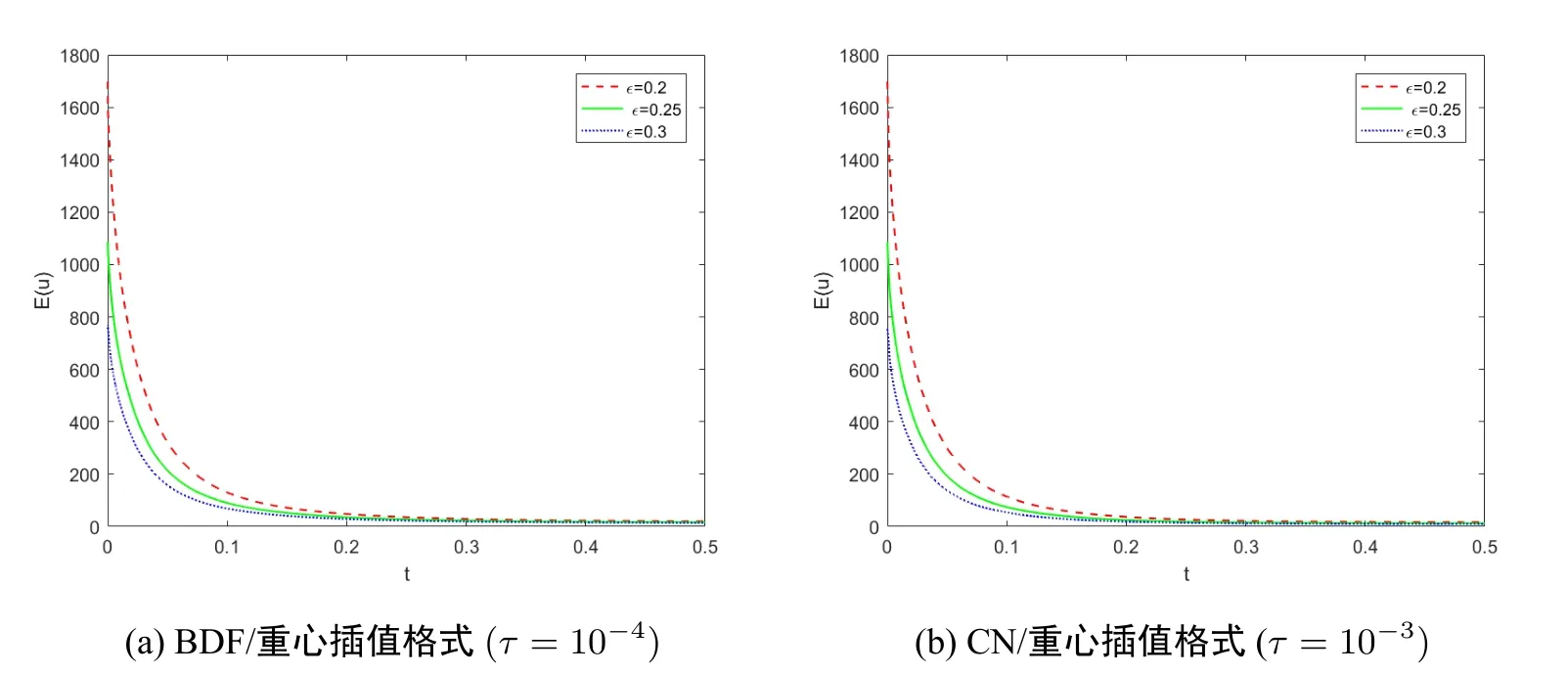
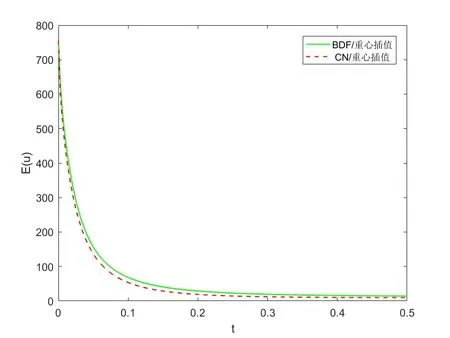
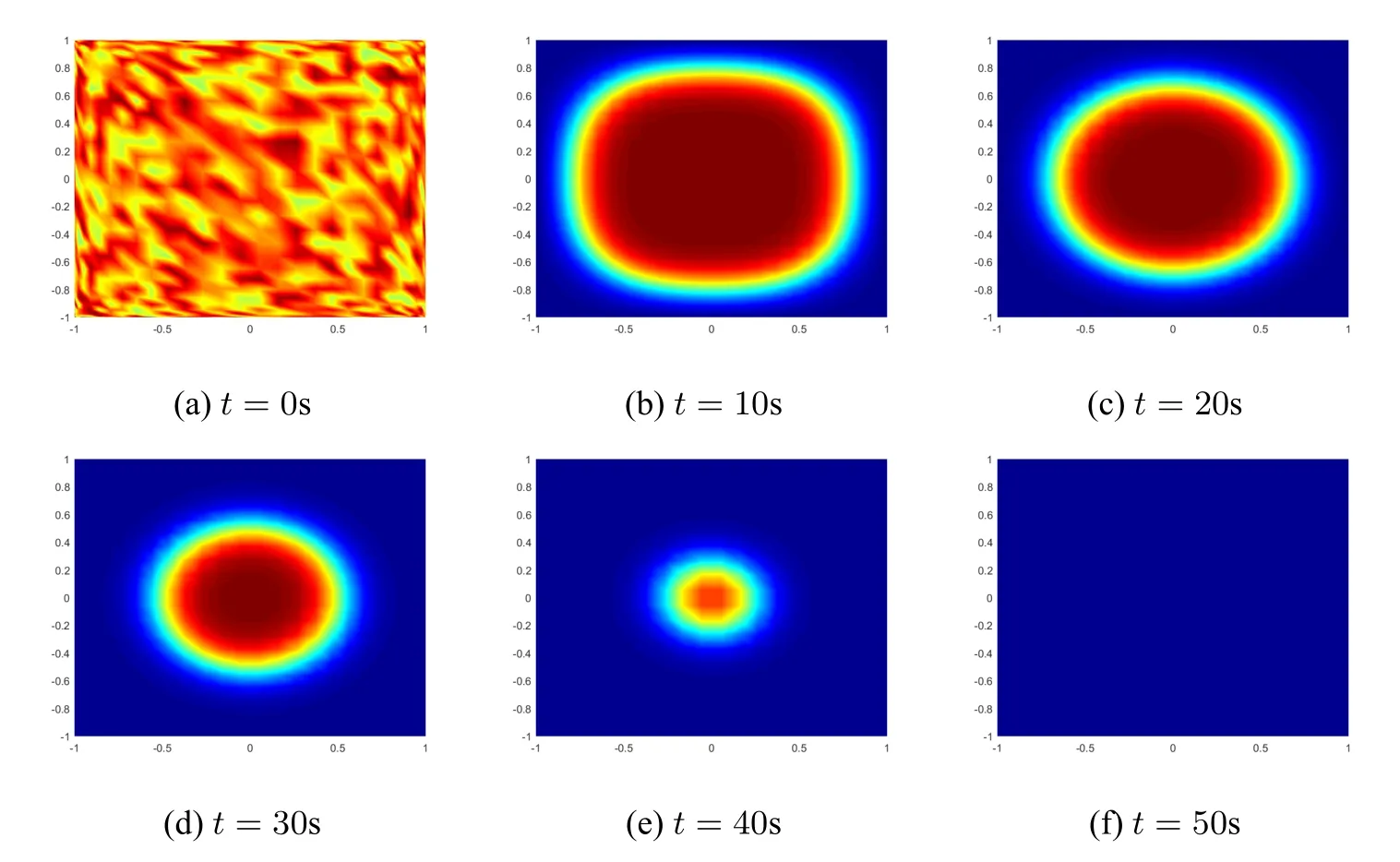
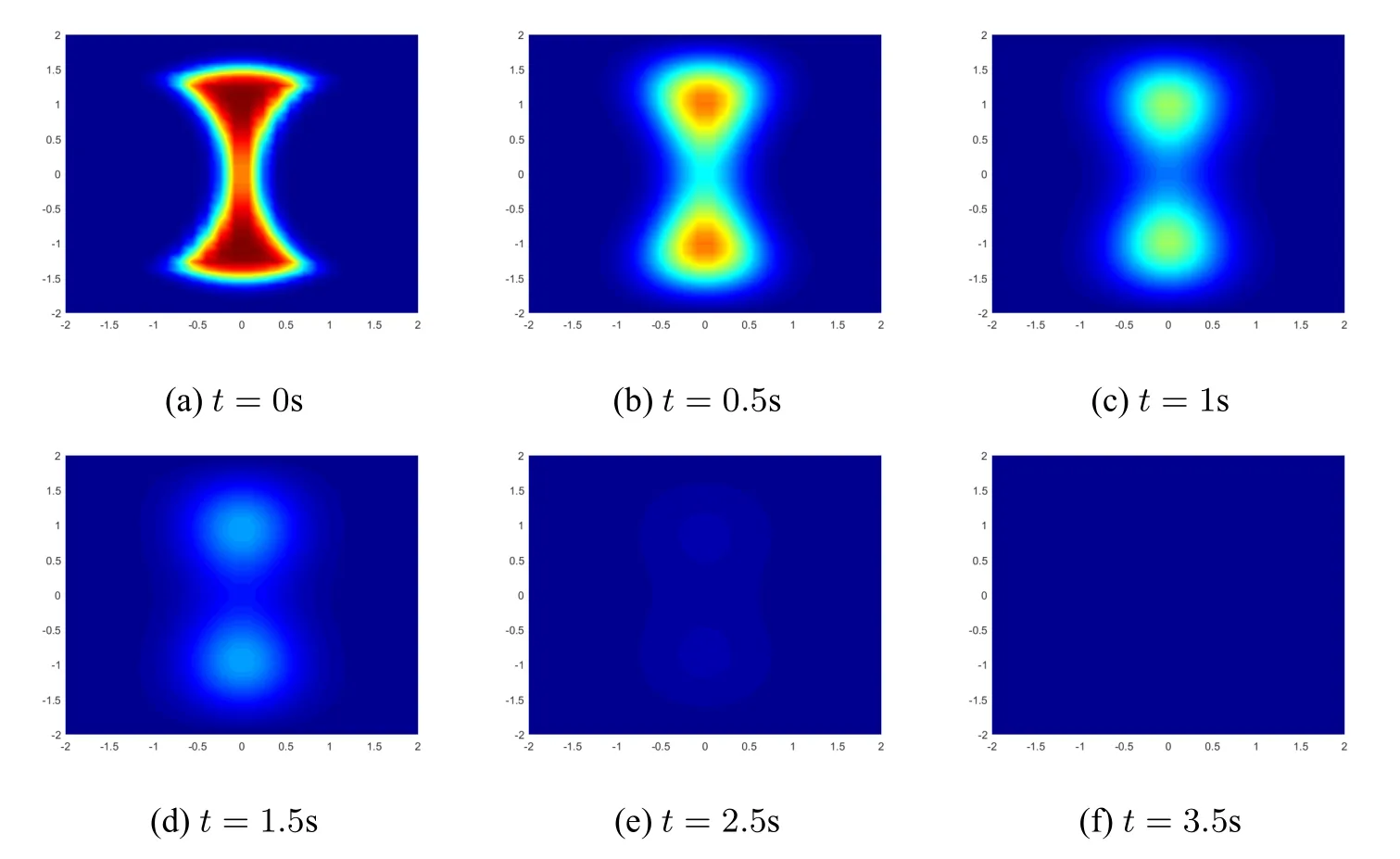
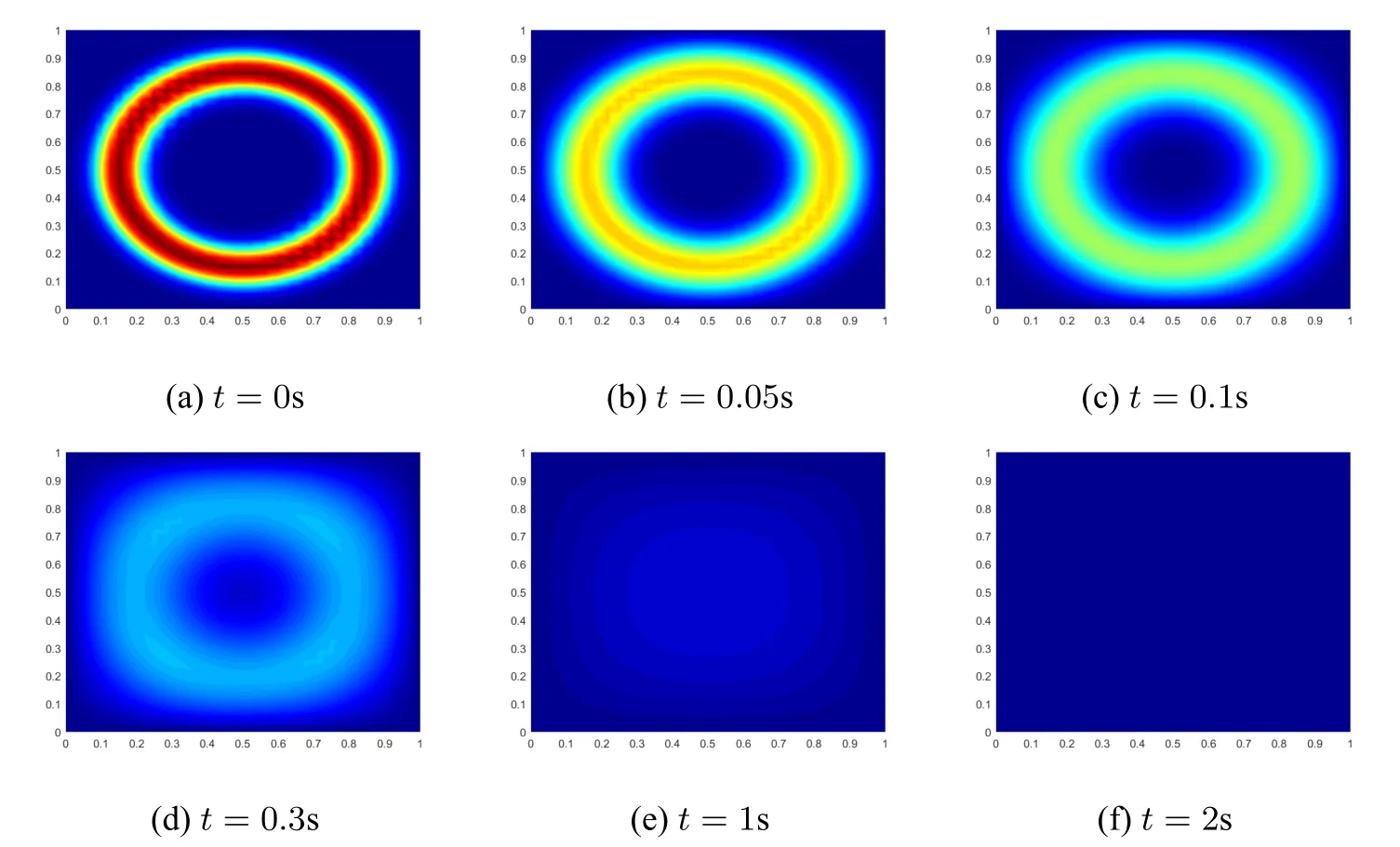
将区间[a,b] 离散为m+1 个第二类chebyshev 节点:a=x0 将其代入Allen-Cahn 方程,可得m+1 个方程 其中U=[u0(t),u1(t),···,um(t)]T. 设p(x)为u(x)的重心Lagrange 插值近似函数.定义误差函数 下面,给出重心插值配点法的逼近性质. 引理2.1([20])如果u(x)∈Cm+1[a,b],则有 为了讨论一维Allen-Cahn 方程的空间半离散格式(2.4)的相容性,定义算子 易知,对于Allen-Cahn 方程的未知函数的重心插值近似函数(2.2),有Γu(xm,t)=0 和=0. 定理2.1 如果u(x,t)∈Cm+1[a,b]×C0[0,T],由重心Lagrange 插值配点法得到的方程(2.4)的数值解为u(xm,t),且方程的非线性项满足Lipschitz 条件,则有: 证明 其中, 对R1,我们有 再由引理2.1,可得 同样地,对R2与R3,我们分别有 结合(2.6),(2.7),(2.8),可得 其中C=.证毕. 通过对空间方向的离散,一维Allen-Cahn 方程转换为关于时间变量t的一阶常微分方程.对于空间重心插值半离散系统(2.4),我们将在时间方向上分别采用向后差分法和Crank-Nicolson 方法设计方程的全离散格式. 将时间域[0,T]等距剖分为n份,得到n+1 个时间节点:tk=kτ,τ=T/n,k=0,1,···,n.令Uk=U(tk).对方程的非线性项采用显格式处理,时间方向采用向后差分离散,可得 整理可得如下一阶半隐全离散格式: 对方程(2.1)的Dirichlet 边值条件u(a,tk)=θ(tk),u(b,tk)=ω(tk),0≤k≤n,按下述方法离散化. 与一阶格式相同,等距剖分时间域,然后对方程(2.4)的非线性项采用显格式处理,时间方向采用Crank-Nicolson 格式离散,可得: 将式(3.3),(3.4)代入(3.2),整理后即可得一维Allen-Cahn 方程的二阶半隐全离散格式: 考虑二维Allen-Cahn 方程的初边值问题: 本节对方程的非线性项f(u)=u-u3仍用显格式处理,对方程的空间方向基于重心Lagrange 插值配点法进行离散,时间方向采用差分格式进行离散,给出Allen-Cahn 方程的数值格式. 与一维Allen-Cahn 处理方式相同,将方程的矩形空间域Ω=[a,b]×[c,d]离散为(m+1)×(l+1)个第二类Chebyshev 节点:a=x0 其中,U=,ui(t)=[ui0(t),ui1(t),···,uil(t)]T,i=0,1,···,m,f(U)=U-U3为方程的非线性项. 一阶半隐全离散格式对(4.2)的非线性项采用显格式处理,时间方向采用向后差分格式离散,可得到方程(4.1)的一阶半隐全离散格式: 二阶半隐全离散格式对(4.2)的非线性项采用显格式处理,时间方向采用CN 格式离散,可得到方程(4.1)的二阶半隐全离散格式: 设p(x,y)为u(x,y)的重心Lagrange 插值近似函数.定义误差函数: 引理4.1([20]) 如果u∈,则有如下估计: 关于Allen-Cahn 方程二维全离散格式的相容性,我们有如下的定理. 定理4.1 设u(x,y,t)∈×C4(0,T],Ω=[a,b]×[c,d].采用CN 格式、重心Lagrange插值配点法得到的非线性格式的数值解记为uh(xm,yl,tn).如果非线性项f(u)满足Lipschitz 条件,则有: 证明设对方程(1.1)在时间方向采用CN 格式离散得到的数值解为.则 然后对(4.5)在空间方向利用重心Lagrange 插值配点法进行离散,可得 其中,ηm,l是空间截断误差. 由式(4.5)和(4.7),有 由非线性项满足Lipschitz 条件及引理4.1,类似定理2.1 的推导,可得: 再利用(4.6)即可得到定理的结论.证毕. 下面通过算例验证上文给出的两种格式的有效性.绝对误差Erra和相对误差Errr定义如下: 其中,uc和ue分别是方程(1.1)或(4.4)的数值解和精确解,∥·∥∞为矩阵的无穷范数. 考虑如下二维Allen-Cahn 方程:Ω={(x,y,t)|0≤x≤1,0≤y≤1,0≤t≤1}, 其中h(x,y,t)=-sin(πx)sin(πy)sin(t)+sin3(πx)sin3(πy)cos3(t)-(1-2επ2)sin(πx)sin(πy)cos(t).该方程的精确解为u=sin(πx)sin(πy)cos(t). 为了验证方程(5.1)的BDF/重心插值格式(4.3)和CN/重心插值格式(4.4)的时间收敛阶,取参数ε=0.1,M=m+1=L=l+1=10,及不同的时间步长τ,计算结果见表1.表中Rate=log 2(Errr2/Errr1)/log 2(τ2/τ1). 表1 方程(5.1)两种离散格式的时间收敛阶(ε=0.1,M=L=10) 由表1可知,BDF/重心插值格式的时间收敛阶为1,CN/重心插值格式的时间收敛阶为2,且随着时间步长τ的减小,相对误差Errr不断减小. 表2显示了在固定参数ε=0.3,τ=10-4,改变空间节点数(M,L)时,时间一阶半隐配点格式的绝对误差和相对误差结果.由表2 可知,随着空间节点的增加,数值解的相对误差越来越小. 表2 方程(5.1)两种离散格式的误差(ε=0.3,τ=10-4) 下面,我们将本文给出的CN/重心插值格式与空间方向分别采用二阶中心差分离散和紧差分离散的两种经典格式的精度进行比较,数值结果如表3所示. 表3 不同空间离散格式的精度对比(ε=0.3,τ=10-4) 从表3可知,与空间方向采用中心差分的格式比较,重心插值使用6×6 个节点达到的精度比二阶中心差分使用32×32 个节点达到的精度还高;重心插值使用10×10 个节点达到的精度比紧差分使用32×32 个节点达到的精度要高得多. 由三种空间离散格式的收敛精度图(图1)可以看出,重心插值配点法的误差从10-2下降到10-8,具有指数收敛的性质. 图1 不同空间离散格式的收敛精度(ε=0.3,τ=10-4,M=L) 考虑如下二维Allen-Cahn 方程:Ω={(x,y,t)|-1≤x≤1,-1≤y≤1,0≤t≤0.5}, 其二维能量函数的离散形式为: 其中hi=xi-xi-1,hj=yj-yj-1. 首先,对BDF/重心插值格式(4.3),取τ=10-4,M=L=10,在不同的参数值ε下计算该方程相应数值解的能量函数,结果如图2(a) 所示.其次,对CN/重心插值格式(4.4),取τ=10-3,M=L=10,在不同的参数值ε下计算该方程相应数值解的能量函数,结果如图2(b)所示. 图2 方程(5.2)两种格式的能量函数图(M=L=10) 由图2可知,方程(5.2)的两种数值格式的能量函数都随时间递减,且ε越大,能量越早达到稳态. 图3是取参数ε=0.3,τ=10-3,M=L=10 时,方程(5.2)的两种不同格式的能量函数图,可以看出,CN/重心插值格式的能量函数线先达到稳定状态,说明其精度更高. 图3 方程(5.2)的两种不同格式能量函数图(ε=0.3,τ=10-3,M=L=10) 考虑如下二维Allen-Cahn 方程:Ω={(x,y,t)|-1≤x≤1,-1≤y≤1,0≤t≤50}, 取参数ε=0.01,τ=10-2,M=L=30.方程(5.3)的二阶半隐配点格式的数值解快照图像如图4所示.由图可以观察到随机生成的无序界面逐渐变淡直至到达稳定状态. 图4 方程(5.3)的二阶半隐格式的数值解在不同时刻t 的快照图像(ε=0.01,τ=10-2) 考虑如下二维Allen-Cahn 方程:Ω={(x,y,t)|-2≤x≤2,-2≤y≤4,0≤t≤4}, 取参数ε=0.1,τ=10-3,M=L=40.二阶半隐配点格式数值解的快照图像如图5所示.由图可以观察到连接的界面逐渐分成两个曲面,然后慢慢变小变圆直至最后消失. 图5 方程(5.4)二阶半隐格式的数值解在不同时刻t 的快照图像(ε=0.1,τ=10-3) 在Ω=[0,1]2×[0,T]上考虑带初值条件 的Allen-Cahn 方程. 设置参数为ε=0.03,τ=10-3,T=2.该方程的二阶格式的数值解在不同时刻的快照图像如图6所示.由图可以看出,圆环随着时间的推移逐渐变淡直至消失. 图6 方程的二阶阶半隐格式的数值解在不同时刻t 的快照图像(ε=0.03,τ=10-3) 本文分别将向后欧拉格式和Crank-Nicolson 格式与重心Lagrange 插值Chebyshev 配点法方法相结合,建立求解Allen-Cahn 方程的数值格式,并对方程的空间一维半离散格式和二维全离散格式的相容性进行了分析.针对方程的非线性项采用显格式处理,避免了非线性迭代而带来的大计算量,提高了计算效率.通过与经典的两种差分格式进行比较,数值算例表明我们的数值格式可以用较少的节点达到较高的精度并满足能量递减规律.本文的重心插值半隐配点格式可推广到其他非线性微分方程,为解决同类问题提供参考.2.2 一维Allen-Cahn 方程空间半离散格式的相容性
3 一维Allen-Cahn 方程的全离散格式
3.1 一阶半隐全离散格式
3.2 二阶半隐全离散格式
4 二维Allen-Cahn 方程的数值格式
4.1 二维重心Lagrange 插值半离散系统
4.2 二维全离散格式
4.3 二维Allen-Cahn 方程全离散格式的相容性
5 数值实验
5.1 算例1
5.2 算例2
5.3 算例3
5.4 算例4
5.5 算例5
6 总结
