基于反射系数谱Z变换的电缆缺陷定位方法

2024-01-22王尉军

绝缘材料 2024年1期

王尉军，陈旻，殷慧，李原

（1. 贵州电网有限责任公司贵阳供电局，贵州贵阳 550004；2. 四川大学电气工程学院，四川成都 610065）

0 引言

交联聚乙烯（crosslinked polyethylene，XLPE）电力电缆具备优异的力学性能与电气性能，被广泛应用于输配电线路中[1-2]。在长期运行过程中，电力电缆会因挤压、受潮、腐蚀等外界因素影响，产生不可逆转的局部缺陷，容易造成电缆故障，影响输配电线路的运行可靠性[3-4]。因此对电缆的局部缺陷进行定位具有重要的研究价值[5]。

目前，电缆的局部缺陷定位方法主要有时域反射（time-domain reflectometry，TDR）法[6-7]和频域反射（frequency domain reflectometry，FDR）法[8]。TDR法是通过注入的脉冲信号在行波反射过程中的时延差来估计缺陷的位置，但是由于脉冲信号中高频信号能量占比较低，并且高频信号能量的衰减特性更强，该方法对缺陷定位的灵敏度较低。

FDR 法是采用宽频阻抗谱[9]或反射系数谱[10]的分析结果来估计缺陷的位置，由于宽频阻抗谱或反射系数谱是采用扫频的方法进行测试，FDR 法中高频信号的能量占比更高，因此其对缺陷定位的灵敏度更高。文献[11-12]使用积分变换方法分析宽频阻抗谱或反射系数谱，有效定位了电力电缆的物理性结构缺陷，但是要求以电缆完好状态下的相关特征量作为参考，导致该方法在实际工程上的应用局限性较大。文献[13-14]使用快速傅里叶变换算法分析宽频阻抗谱或反射系数谱，实现了电力电缆的缺陷定位，但傅里叶变换算法要求采样数据与变换后的数据具有相同的点数，并且变换后的数据会平均分布在所有的时域或频域范围内，导致最终缺陷定位的分辨率较低，并且无效数据量较多，影响缺陷定位的结果。文献[15-16]利用加Kaiser窗的离散傅里叶变换算法分析宽频阻抗谱或反射系数谱，对微小缺陷的定位灵敏度更高，但存在参数难以选定与计算冗余度较高的问题。因此，研究缺陷定位分辨率更高与数据冗余度更低的FDR 电缆缺陷定位方法具有重要意义。

针对上述传统方法存在的问题，本文提出基于反射系数谱Z 变换的电缆缺陷定位方法，并设计含有缺陷的电缆模型与真实电缆，对其开展缺陷的定位分析，论证该方法的准确性与优越性。

1 电缆反射系数谱

1.1 电缆分布参数模型

根据传输线[17]理论，当电缆线路的长度远大于入射信号的波长时，需要将电缆线路视为分布参数网络，其具体的等效电路模型如图1所示。

图1 分布参数网络的等效电路模型Fig.1 Equivalent circuit model of distributed parameter network

图1 中，电缆线路中单位长度的电阻、电感、电导和电容分别用R0、L0、G0、C0表示。由于电缆线路存在趋肤效应与临近效应，R0、L0会受信号频率f的影响，当f增大时，R0增大，L0减小。通常情况下，R0与L0可以由式（1）～（2）近似得到[18-19]。

式（1）～（2）中：ω是入射信号的角频率；μ0是真空磁导率；rc是缆芯的半径；rs是屏蔽层的半径；σc是缆芯材料的电导率；σs是屏蔽层材料的电导率。

G0、C0则不受f的影响，仅与电缆自身的结构特性相关，可以由式（3）～（4）计算得到[18-19]。

式（3）～（4）中：σJ是绝缘层材料的电导率；εJ是绝缘层材料的介电常数。

1.2 缺陷电缆的反射系数谱

对图1中分布参数网络的等效电路模型进行分析，当电缆的长度为l时，可以得到电缆中距首端x处的电压U(x)与电流I(x)分别表示为式（5）～（6）。

式（5）～（6）中：U1是入射电压波；U2是反射电压波；γ是电缆的传播常数；Z0是电缆的本体特征阻抗。

γ和Z0可以分别表示为式（7）～（8）。

式（7）～（8）中：α是电缆的衰减常数；β是电缆的相位常数，可以表示为式（9）。

式（9）中，v表示电缆中的波速。

在电缆中距首端x处的反射系数Γ(x)被定义为反射电压波与入射电压波的比值，如式（10）所示。

式（10）中，ZL是电缆末端处的阻抗。

通常情况下，在开展电缆的反射系数谱测试时，电缆的末端会处于开路状态，此时ZL=∞，得到Γ(x)如式（11）所示。

分析电缆的首端位置，此时x=0，得到反射系数谱Γ(0)如式（12）所示。将式（7）代入式（12）可以得到式（13）。

如图2 所示，对于总长度为l的电缆而言，假如该电缆在距首端l1～l2处存在局部缺陷，令局部缺陷段的特征阻抗为Zq，传播常数为γq，得到电缆中l1、l2位置的反射系数与特性阻抗分别为式（14）～（17）所示。

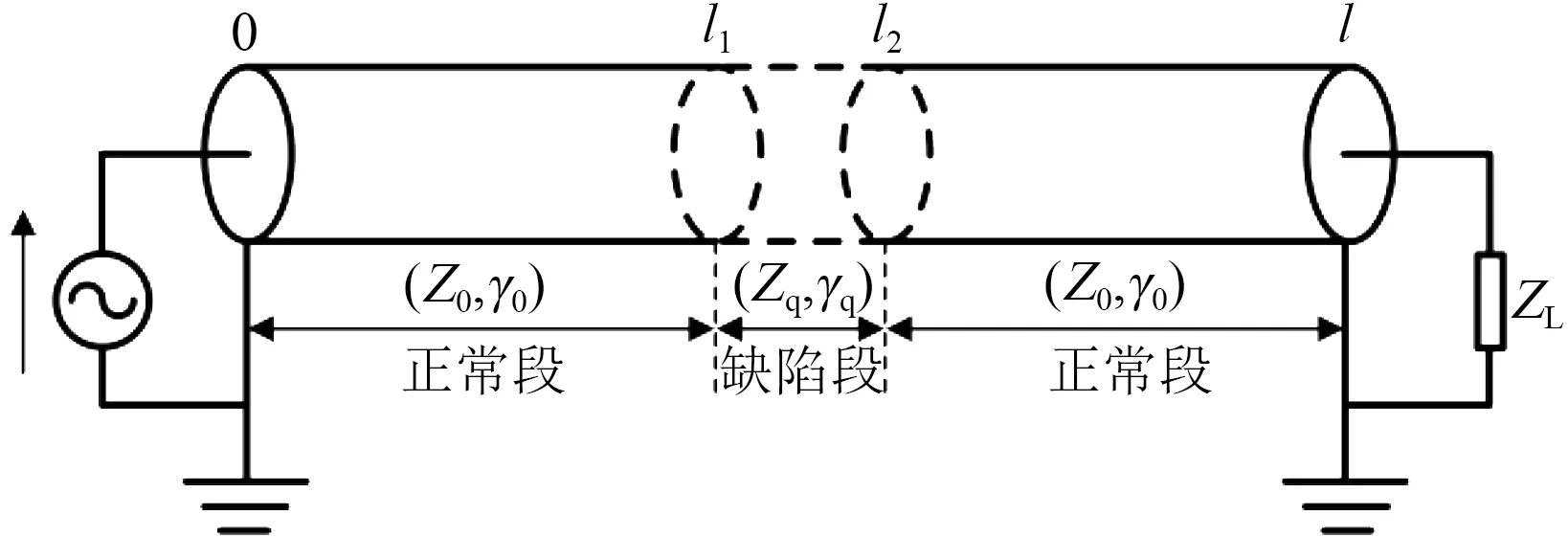
图2 含局部缺陷的电力电缆Fig.2 Power cable with local defect

进一步可以得到电缆首端的反射系数如式（18）所示。

当电缆中出现缺陷时，物理性结构破坏、水树、电树、绝缘老化等现象会导致电缆中局部区域的电容发生变化[15-16]，进而造成电缆中该区域的分布参数模型发生变化，影响电缆的反射系数谱。在50 m的10 kV XLPE 电力电缆上25 m 处设置局部缺陷，令局部缺陷段的单位电容C0为完好电缆的0.8 倍，得到完好电缆与含局部缺陷电缆的反射系数谱数据如图3 所示。从图3 可以看出，当电缆中含有缺陷时，缺陷位置的电缆本体特征阻抗会产生变化，导致反射系数谱与完好电缆的反射系数谱出现明显的差异，因此可以利用反射系数谱对电缆中缺陷进行定位分析。

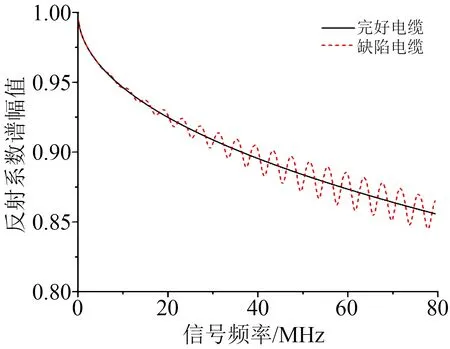
图3 50 m电力电缆的反射系数谱Fig.3 Reflection coefficient spectrum of 50 m power cable

从图3还可以看出，随着信号频率的升高，反射系数谱的幅值逐步下降，这是由于高频信号的能量在电缆中衰减迅速造成的。但是在高频范围内，缺陷电缆的反射系数谱与完好电缆的反射系数谱存在明显差异，该差异与缺陷的位置有关，当信号频率进一步升高时，反射系数谱的幅值会继续下降，导致信号被噪声淹没，因此反射系数谱的测试频率区间受最终测试结果的信噪比影响。

2 电缆缺陷定位算法

传统方法利用快速傅里叶变换算法对采集的反射系数谱进行分析，将频域数据转化为时域数据，但该方法在实际应用时仍存在一些不足。一方面，由于快速傅里叶变换算法中时域数据与频域数据的点数是一致的，且变换后的数据会平均分布在所有的时域或频域范围内，传统方法得到的时域数据中大部分信息是冗余的，冗余信息不仅与电缆的缺陷定位结果无关，而且可能引入干扰峰，影响缺陷定位结果的判断；另一方面，当反射系数谱的测试点数较少时，在快速傅里叶变换算法中变换数据量一致性的影响下，传统方法获取的时域数据的数据量也较少，导致时域数据曲线的分辨率较低，进一步造成最终缺陷定位函数的采样率较低，容易出现栅栏效应，难以对电缆缺陷进行准确定位。

2.1 线性调频Z变换

线性调频Z 变换能够在Z 平面中不同起止时间位置的螺旋线上进行均匀采样，从而得到特定时间区域内的数据变换结果[17-18]。对于离散数据信号y(n)而言，其线性调频Z 变换结果Y(z)如式（19）所示。

式（19）中，N是y(n)的数据点数；n为离散数据信号y(n)的计数变量。

在Z平面中一段螺旋线上设置等间距角的抽样点，得到抽样点zk如式（20）所示。

式（20）中：M是zk的数据点数；A是螺旋线上起始抽样点z0的特征复数；W是螺旋线上抽样路径的特征复数；k是zk的计数变量。

A和W可分别表示为式（21）和式（22）。

式（21）～（22）中：A0是螺旋线上起始抽样点z0的矢量半径长度；θ0是螺旋线上起始抽样点z0的相角；φ0是螺旋线上抽样相位差，当φ0＞0 时，螺旋线是逆时针旋转，当φ0＜0时，螺旋线是顺时针旋转；W0是螺旋线的伸展率，当W0＞1 时，螺旋线呈内缩状态，当W0＜1 时，螺旋线呈外伸状态，当W0=1 时，螺旋线呈现为等半径圆弧。

通过式（19）～（22）可得到式（23）。

线性调频Z 变换的具体采样原理如图4 所示。从图4 与式（23）可以看出，利用线性调频Z 变换可以将已知的频域数据转化为任意范围的时间数据，并且可以提高时间数据的分辨率。

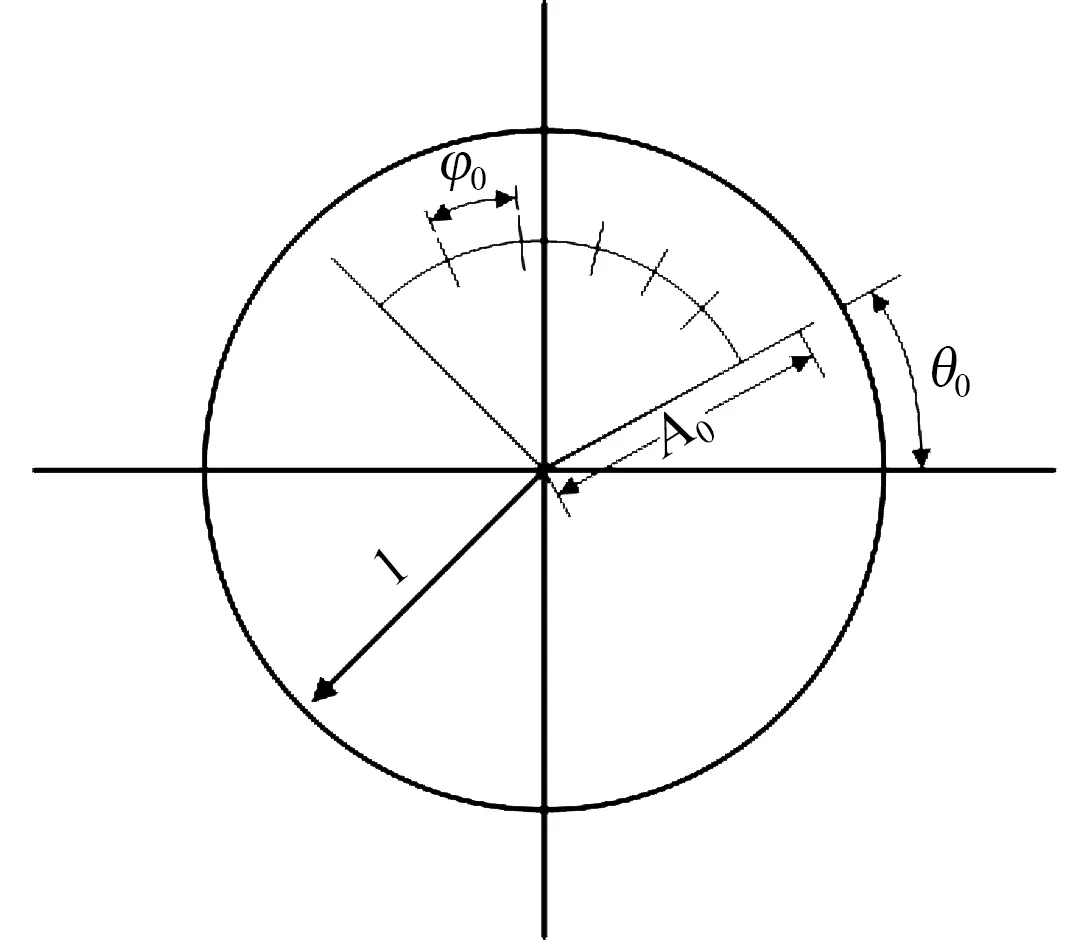
图4 线性调频Z变换的采样原理图Fig.4 Sampling schematic diagram of linear frequency modulated Z transformation

2.2 基于反射系数谱Z变换的电缆缺陷定位方法

利用Z 变换对反射系数谱数据进行分析时，需要确定待分析的电缆长度范围，因此设定缺陷定位区间的最大值、最小值与分辨率分别为xmax、xmin、Δx，实际测试中可以根据测试效果自由选定上述相关参数。

根据式（13）可知，对于总长度为l的电缆的末端反射波，其时域数据上对应的时延是2l/v，因此，对于xmin与xmax而言，其时域数据上对应的时延分别是2xmin/v、2xmax/v，得到待转换时域数据的范围是[2xmin/v，2xmax/v]。根据该时域数据范围，可以确定Z变换中参数θ0、φ0、M分别如式（24）～（26）所示。

式（24）～（26）中，floor 表示向下取整；fs为离散数据信号y(n)的采样频率。

由式（13）可知，在衰减常数的影响下，反射信号的幅值与缺陷距首端的距离成反比，不利于远距离缺陷的定位分析。Z 变换中W0可以控制变换螺旋线的伸展率，因此本研究通过设置W0＜1，将螺旋线设置为外伸状态，从而提升远距离缺陷的反射信号幅值。为了防止计算时数据溢出，将W0设置为式（27）。

式（27）中，N为离散数据信号的数据点数。

同时为了方便起见，设置A0=1。需要说明的是，由于反射系数谱是频域数据，为了利用Z变换将频域数据转化为时域数据，需要对原始采样数据进行共轭处理，得到本文方法的缺陷定位函数D(k)如式（28）所示。

式（28）中，*表示取复数的共轭。

在时域数据与频域数据的转化过程中，数据的截断效应会引发频谱泄漏的问题，导致缺陷产生的旁瓣噪声掩盖微小缺陷的反射信号，给缺陷的定位分析带来误差[15-16]。针对这种现象，通常采用加窗法来减少频谱泄漏的影响，本文选用经典窗函数Hanning 窗[19]对频域数据开展加窗处理，得到加窗处理后的缺陷定位函数T(k)如式（29）所示。

式（29）中，wH(n)是Hanning 窗函数，具体形式见文献[19]。

由式（29）可知，在测试获取电缆的反射系数谱后，利用本文所提方法对反射系数谱开展分析，便可以定位电缆中的缺陷，无需完好电缆的参考数据。结合式（24）～（26）、（29）可以看出，线性调频Z变换可任意调节缺陷定位函数的分辨率Δx，以提升处理结果中波形的分辨率，展示缺陷定位函数的波形细节，实现电缆缺陷的精准定位。

3 缺陷定位的仿真研究

本文将10 kV XLPE 电力电缆作为样本，开展缺陷定位的仿真研究，以验证本文所提方法的有效性与优越性，该仿真电缆模型的结构与尺寸如图5所示。利用图5 中缺陷电缆的结构模型对5 种缺陷状态的150 m 10 kV XLPE 电力电缆样本进行数值仿真，分别编号为1#、2#、3#、4#、5#，仿真的具体参数如表1 所示，仿真结果如图6 所示。在本次的仿真研究过程中，对测试夹具的影响进行了简易的数值仿真。

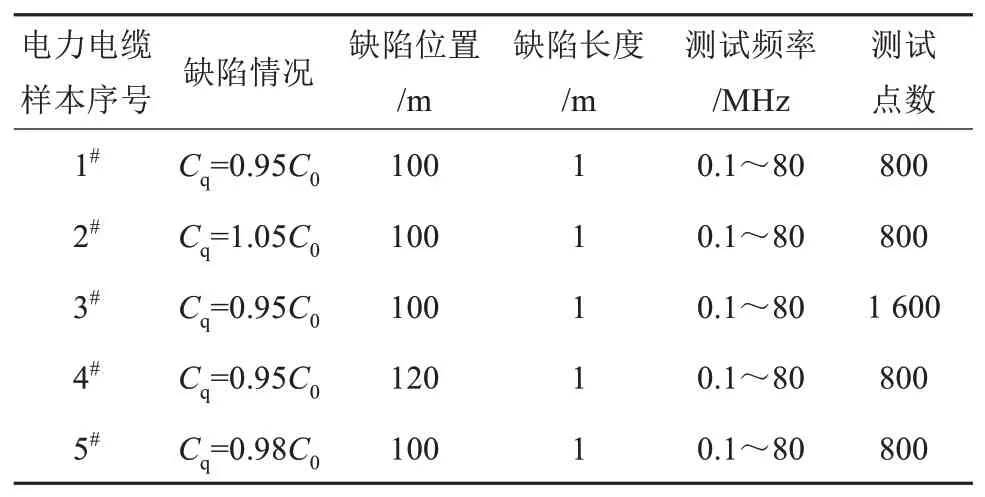
表1 仿真电力电缆模型的缺陷Tab.1 Defects of simulation power cable models

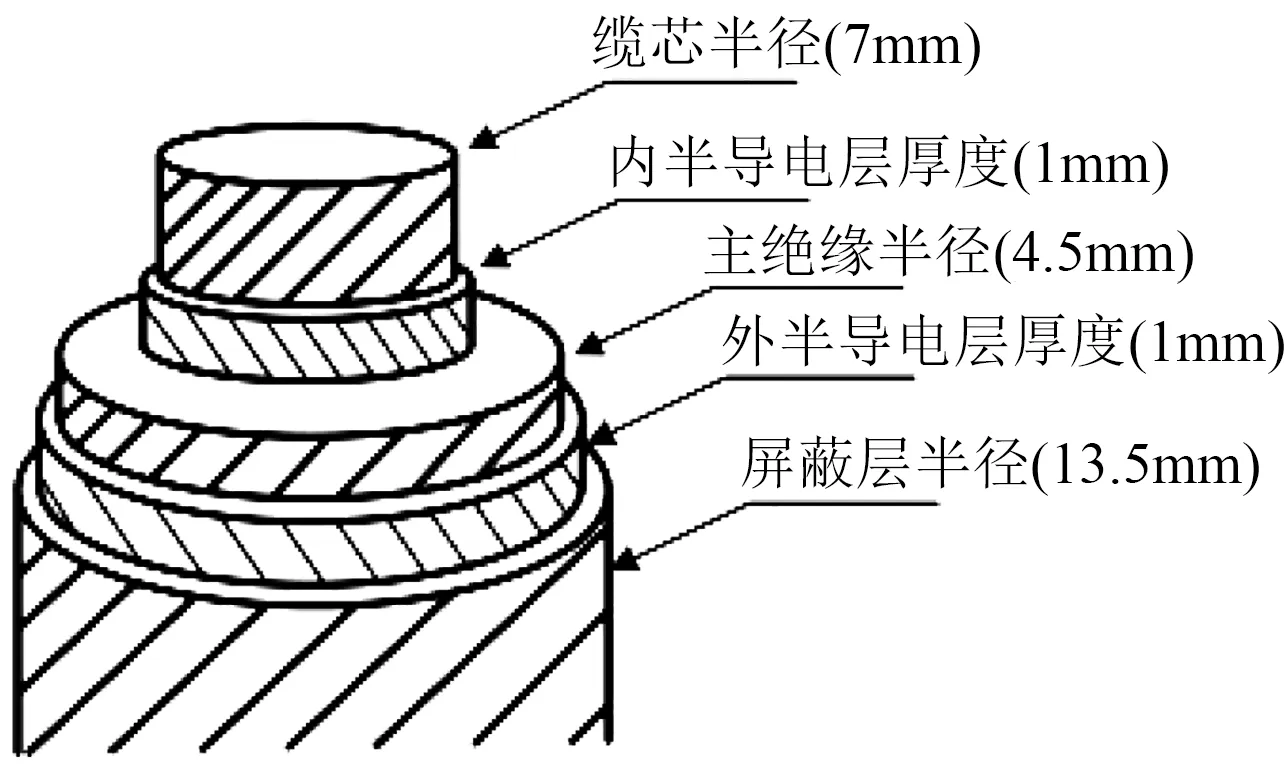
图5 仿真电缆模型的结构与尺寸Fig.5 Structure and size of simulation cable model

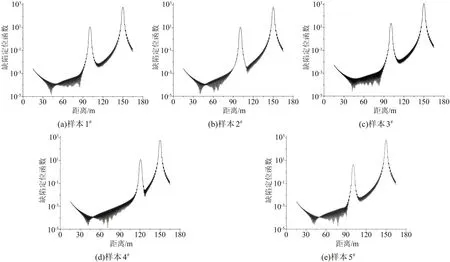
图6 本文方法对受损电力电缆样本的仿真结果Fig.6 Simulation results of damaged power cable samples by the proposed method

由图6 和表1 可知，1#～5#仿真电缆样本的缺陷定位位置分别为100.65、100.65、100.65、120.60、100.65 m，定位的绝对误差分别为0.65、0.65、0.65、0.60、0.65 m，说明本文提出的方法可以准确定位电缆中的缺陷，且定位的绝对误差较小。由样本1#与样本2#的定位结果可见，本文所提的缺陷定位函数可有效定位电缆中不同类型的缺陷；由样本1#与3#的定位结果可见，本文所提的缺陷定位函数受测试点数的影响较小；由样本1#与4#的定位结果可见，本文所提的缺陷定位函数能有效定位电缆中不同位置处缺陷；由样本1#与5#的定位结果可见，本文所提的缺陷定位函数能有效定位电缆中不同受损程度的缺陷。综上所述，本文所提的缺陷定位函数能有效定位电缆中不同类型、不同程度与不同位置的电缆缺陷，且受测试点数的影响较小，具有较好的实际工程应用价值。

为了与传统方法进行对比，本文利用文献[13-14]中快速傅里叶变换算法对样本1#的测试数据进行分析，结果如图7 所示。由图6(a)与图7 可见，由于传统方法中快速傅里叶变换前后的数据点数是一致的，传统方法中缺陷定位结果中存在大量的无效数据，导致最终的缺陷定位函数存在干扰的特征峰，难以判断真正的电缆缺陷特征峰。并且传统方法的缺陷定位结果中波形的分辨率较低，波形的细节存在失真现象。而本文提出的方法采用了线性调频Z 变换，可以控制仅获取特定电缆长度范围内的时域数据，降低了数据的冗余度，简化了数据分析结果，能够有效减少误判干扰。此外，本文提出的方法中线性调频Z变换可以提升处理结果中波形的分辨率，展示缺陷定位函数的波形细节，有利于缺陷的精准定位。

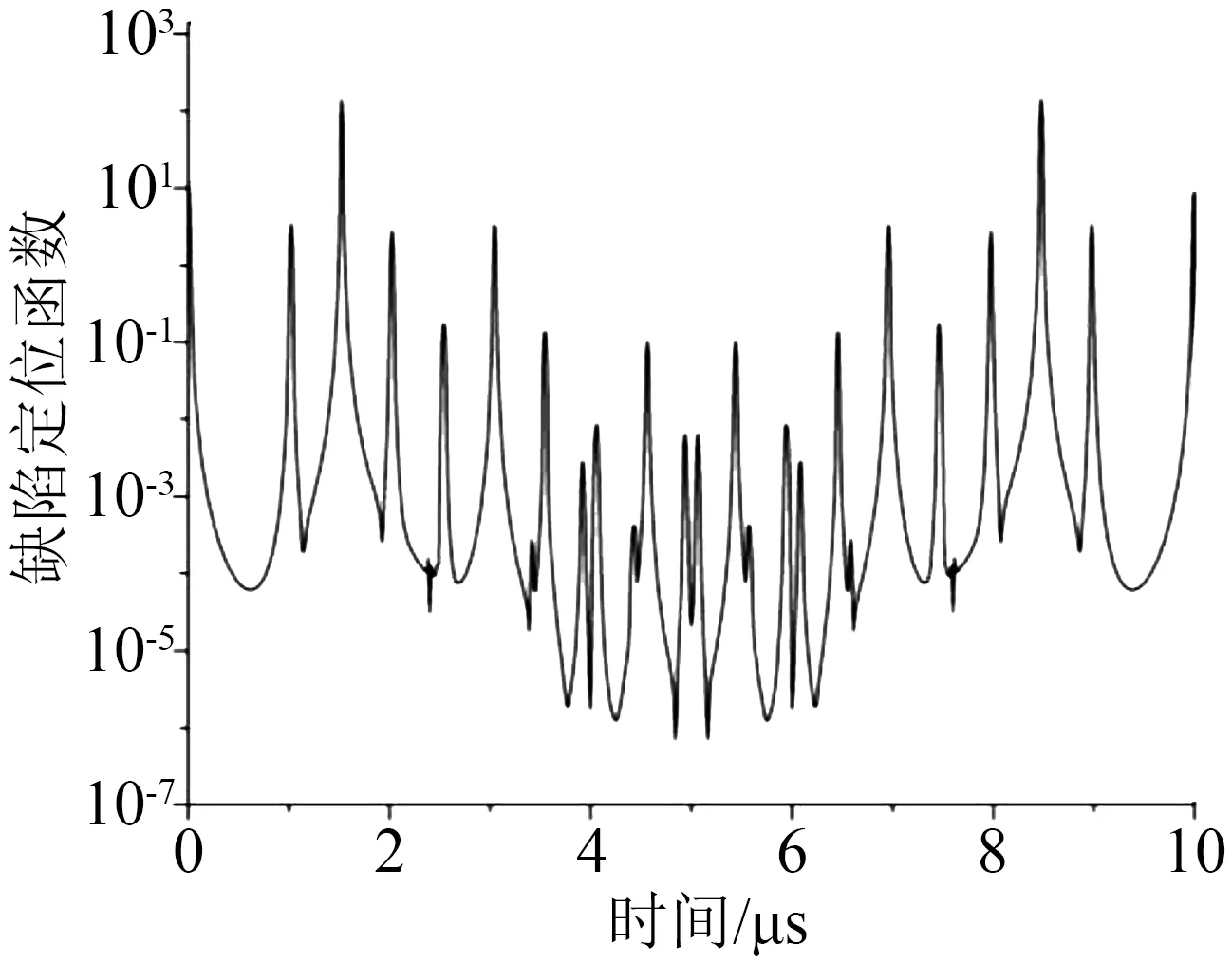
图7 传统方法中受损电缆样本仿真结果Fig.7 Simulation result of damaged power cable sample by traditional method

4 实验验证

为了研究本文所提方法对真实XLPE 电力电缆中缺陷的定位能力，在500 m 的10 kV XLPE 电力电缆上设计屏蔽层受损缺陷，缺陷长度为1 m，缺陷位置距首端250 m，但是缺陷位置处两端的屏蔽层仍保持电气连接，用于模拟XLPE 电力电缆受到外力破坏导致的电缆结构受损情况。图8为实验研究的测试平台，将网络分析仪连接端作为电缆首端，另一端作为电缆的末端，该电缆末端设置为开路状态。网络分析仪的测试频率范围为0.15～10 MHz，测试频率的点数为396。

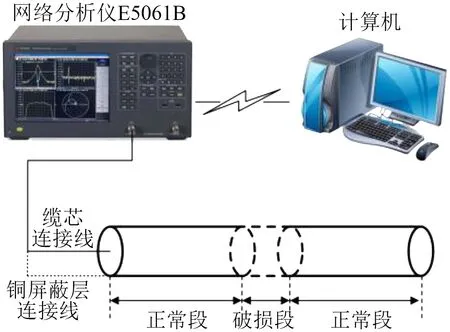
图8 实验平台示意图Fig.8 The experimental platform diagram

将图8 中测试得到的首端反射系数谱进行处理，得到本文所提方法的处理结果如图9 所示。由图9可见，处理结果中函数曲线在250.5 m 出现一个明显峰值，表明缺陷位置距电缆首端250.5 m，绝对定位误差为0.5 m，说明本文所提方法成功定位了电缆的结构受损缺陷。需要说明的是，对于所有的时域反射法与频域反射法而言，当缺陷位置靠近末端时，缺陷的反射波会被末端的强反射波淹没，难以识别，导致在电缆末端位置出现缺陷定位盲区。

图9 本研究方法中受损电缆样本的实测结果Fig.9 Measuration result of damaged power cable sample by the proposed method

为了说明本文所提方法的优越性，利用文献[13-14]中快速傅里叶算法对真实电缆的测试结果进行处理，得到传统方法中缺陷定位函数如图10所示。从图10可以看出，传统方法得到的时域数据中大部分信息是冗余的，该冗余信息不仅与电缆的缺陷定位结果无关，而且引入了大量干扰峰，导致难以判断真正的电缆缺陷，因此传统方法无法直接定位缺陷位置。对比图9 与图10 可见，与传统方法相比，本文所提方法可以提升缺陷定位函数的分辨率，提高缺陷的定位效果；还可以降低数据的冗余度，简化缺陷定位函数，减少了函数曲线中干扰峰，提升了缺陷定位结果的准确性。

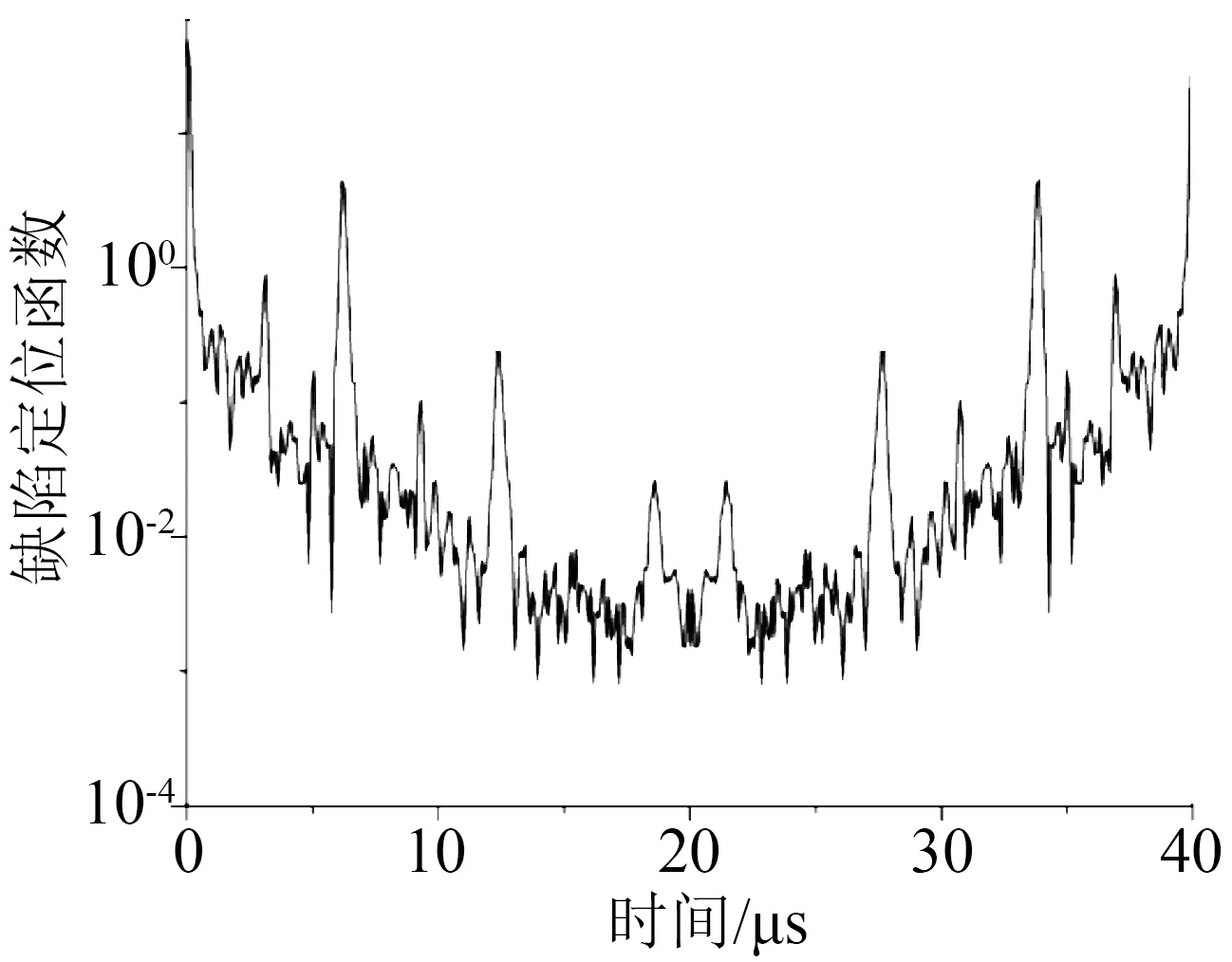
图10 传统方法中受损电缆样本的实测结果Fig.10 Measuration result of damaged power cable sample by the traditional method

在实际电缆的生产过程中，不可能保证每个位置处的结构、材料完全一致，因此与图6中仿真结果对比，图9中实测结果出现了部分杂峰，但是杂峰的幅值较小，明显低于真实缺陷的峰值，不影响对缺陷的判断。并且相比于传统方法，本文所提方法有效降低了数据的冗余度，简化了缺陷定位函数，消除了函数曲线中大部分的杂峰。如果想进一步抑制杂峰的影响，可以与历史数据进行比对，并查找异常变化的峰值点，实现对电缆缺陷的精准定位。实际工程上，也可根据缺陷定位函数的特征峰，找出疑似缺陷点的位置，并辅以人力巡查等方式确定缺陷是否存在。

需要说明的是，在选取反射系数谱的测试频率区间时，可以根据反射系数谱的实际测试结果开展分析。一方面，可以根据文献[8]，通过观察反射系数谱的幅值是否被噪声掩盖来设定反射系数谱的阈值，然后确定测试频率区间；另一方面，可以根据文献[11]，分析反射系数谱的三维缺陷定位图，然后根据反射信号的衰减特性选择合适的测试频率区间。

本文所提方法的重点在于提高传统方法中缺陷定位函数的分辨率，同时降低算法的数据冗余度，消除干扰峰的影响，鉴于篇幅有限，本文仅对文献[15-16]中仿真电容缺陷及实测屏蔽层受损缺陷开展了研究分析，未对所有类型的缺陷开展研究。