地震波斜入射作用下重力坝地震响应分析

陈灯红 曾怡阳 赵艺园 刘云龙 岳 梦

(1.防灾减灾湖北省重点实验室(三峡大学), 湖北 宜昌 443002;2.三峡大学 土木与建筑学院, 湖北 宜昌443002)

在大坝-地基动力相互作用的研究中,工程上最常用的是无质量地基模型[1-2].但地基本身是有质量的半无限体,并没有固定边界,地震波的能量会被地基辐射吸收,若使用无质量地基则无法考虑远域地基的辐射阻尼效应[3].在地震波输入方面,现阶段用于模拟结构地震响应时一般采用垂直入射的方式[4],这种方式对于模拟结构的远场地震响应较为合适.但是,地震波传播到坝体结构时的入射波类型及角度存在一定的不确定性,对于距离结构较近的浅源地震来说一般不是垂直入射的.

为了更加真实地反映坝体在地震作用下的响应,国内外学者针对地震波斜输入问题进行了研究.在地下结构的抗震设计与计算分析中,杜修力等[5-6]研究了不同地震波斜入射下地下结构的时域地震动反应,建立了半空间场地的平面波倾斜输入方法.赵密等[7-8]提出并采用了一种结构-地基动力相互作用的地震波输入方法,以此模拟P波或SV 波以不同角度在成层介质中的输入.周晓洁等[9]实现了地震波斜入射下层状场地地下综合管廊地震反应分析,建立了不同场地条件下地下综合管廊分析模型,分析了SV 波斜入射下的综合管廊结构地震响应.陈灯红等[10]利用Fortran语言对Abaqus软件进行二次开发,将黏弹性边界有效地嵌入到Abaqus中,通过数值算例验证了程序的正确性.孙靖云等[11]研究了地震荷载作用下隧道内油气管道应力响应,说明了轴向地震作用下管道应力、位移较大.刘述虹等[12]进行了典型综合管廊体系的抗震性能数值模拟研究,分析了综合管廊这一浅埋地下构筑物的特性及其震害特点.Heymsfield[13]采用直接边界积分方程法,研究了不同角度下SH 波斜入射时倾斜基岩对地表位移的影响.周鹏等[14]建立了海水-沉管隧道-海床的整体分析模型,基于该模型分析了地震P波斜入射作用下,不同入射角度对沉管隧道结构的动力响应的影响.

在水工结构抗震领域中,苑举卫等[15]将地表地震动时程分量分解为斜入射的平面SV 波和P波,证明了地震波斜入射对重力坝结构影响显著,尤其在坝-基交界面上.朱代富等[16]研究了不同角度地震波入射下的坝体动力响应,证明了动力分析时考虑地震波同时斜入射的必要性.岑威钧等[17]分别研究了SV波和P波斜入射下高面板堆石坝的地震反应特性,证明了常规垂直入射结果相较斜入射偏于保守.杜修力等[18]结合小湾拱坝研究了SV 波斜入射下拱坝的地震响应,表明入射角度对低频区幅值放大系数影响显著.孙奔博等[19]研究了平面SV 波斜入射下重力坝的地震响应,证明入射角度的存在对坝体位移和应力有显著影响.Maeso等[20]基于动力分析的边界有限元模型,研究了不同的简谐波斜入射下拱坝的动力响应.赵密等[21]提出了一种用于近场波动有限元分析的高阶精度人工边界条件,表明了提出的高阶精度人工边界条件具有精确性、稳定性和高效性.王刚等[22]将时间显式积分动力有限元方法与黏弹性动力人工边界理论相结合,采用动力学方法求解静力作用效应,求解了含接触非线性问题的重力坝静、动力荷载组合作用的响应.值得注意的是,上述学者大多针对地震波斜入射情况下的结构动力响应进行了重点研究,但在重力坝静动力响应影响的规律方面还有待深入研究.

基于上述学者对地震波斜入射的研究,本文对该问题进行深入研究,探究P波和SV 波斜入射对重力坝静动力响应影响的规律.在对结构进行地震响应分析时考虑初始应力场[23-24](不仅考虑结构的动力响应情况,还综合考虑了静-动力分析问题),分别推导了P波和SV 波倾斜入射时的等效地震力,构建了考虑地震波斜入射的黏弹性静-动力统一型人工边界.通过用户子程序接口编写二维地震波的波动输入程序,基于有限元软件Abaqus完成地震动输入,以黄登混凝土重力坝为研究对象,研究P波和SV 波在不同斜入射角度下混凝土坝的动力响应.

1 研究方法

1.1 黏弹性人工边界

黏弹性人工边界是一种局部人工边界,它有效地解决了黏性边界的低频失稳问题,能够较好地模拟无限地基的弹性恢复能力和辐射阻尼效应[25].基于Abaqus软件平台在计算模型的人工边界节点的每个方向施加一端固定的单向并联的弹簧和阻尼器元件,以此完成人工边界的施加,对应的公式如下所示:

二维黏弹性人工边界等效物理系统的弹簧系数和阻尼系数分别为[4]:

切向边界

法向边界

式中:R为散射波源至人工边界点的距离;cs、cp为SV 波和P 波波速:G为介质剪切模量;ρ为介质密度;αT、αN分别为黏弹性人工边界切向、法向参数,其中αT取0.5,αN取1.施加弹簧-阻尼元件时只需将式(1)和式(2)乘以边界结点影响面积并施加在该结点上即可(如图1所示).

图1 黏弹性边界示意图

对于黏弹性人工边界的外源波动输入问题,可将总波场uT分解为散射波场uS和自由波场uF:

由位移平衡条件与力学平衡条件,人工边界上任意一点n的运动方程为[26]:

式中:A为结点影响面积;(t)为自由场应力;K nj、C nj分别为边界结点黏弹性组件的弹簧系数和阻尼系数.

1.2 基于黏弹性边界的二维斜入射波动输入方法

1)P波斜入射等效荷载

假设P波以任意角α入射,在入射区域内的任意一点(x,y)的各向位移时程可记为up(t)(计算区域如图2所示),图中反射P 波与反射SV 波的反射角分别为α、β,对应的波幅系数分别为A1、A2,左边人工边界高度为H,下边界和地表面长度为L.

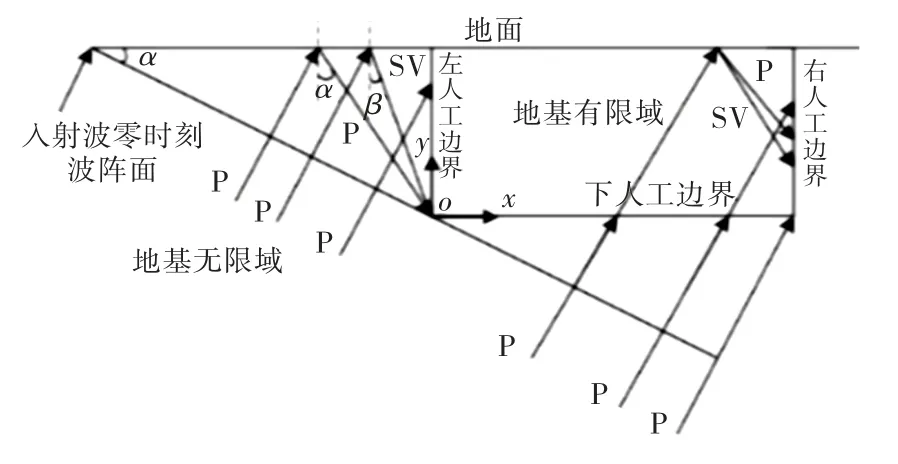
图2 P波斜入射示意图

由Snell定律可得如下关系式[27]:

式中:cs、cp分别为P波和SV 波波速,可由介质特性参数求得.左边界处入射和反射的P 波、反射的SV波相对于入射波up(t)零时刻波阵面的延迟时间分别为

式中:H为左边界的高度;y为竖向坐标值.

左侧边界的内行场位移由直接入射的P波、反射P波和反射SV 波构成,边界节点的位移公式如下:

式中:u lx(t)、u ly(t)分别为水平位移、竖直位移;Δt1、Δt2、Δt3分 别 为 入 射P 波、反 射P 波、反 射SV 波 相对于波阵面的时间延迟.由式(8)求导或差分计算可得对应的速度场.

计算自由波场传播应力需引入局部坐标系(ξ,η),其中ξ为波的传播方向;η为ξ的法线方向,在均匀弹性介质中平面P波ξ方向的传播应力可表示为[28]:

对于平面SV 波在均匀弹性介质中η方向的传播应力可以表示为:

由式(9)、(10)局部坐标系将波场的传播应力转化为全局坐标系,求得左侧人工边界上的应力.结合式(7)～(10)得出左边界的等效节点力如式(11):

地基截断边界的右边界、底边界处节点的等效荷载计算方法与左边界类似.

2)SV 波斜入射等效荷载

假设SV 波以任意角α1入射,在入射区域内的任意一点(x,y)的各向位移时程可记为usv(t)(计算区域如图3所示),图中反射SV 波与反射P 波的反射角分别为α1、β1,对应的波幅系数分别为B1、B2,左边人工边界高度为H,下底边界和地表面长度为L.

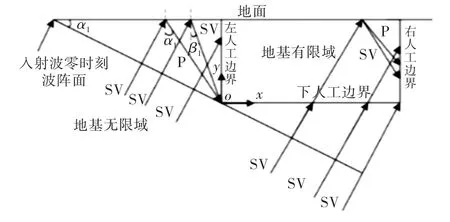
图3 SV 波斜入射示意图

左边界处的入射和反射SV 波、反射P波相对于入射波usv(t)零时刻波阵面的延迟时间分别为:

式中:H为左边界高度;y为左边界竖向坐标值.

左边界内行场位移由入射SV 波、反射P波和反射SV 波构成,边界结点上的位移公式如下:

由式(9)、(10)将波场的传播应力从局部坐标系转化为全局坐标系,求得在左人工边界上的应力.结合式(12)、(13)得出左边界的等效节点力如式(14):

地基截断边界的右边界、底边界处节点的等效荷载计算方法与左边界类似,只需注意应力方向即可.

1.3 考虑静动力边界的统一分析方法

在结构动力响应分析中,通常要考虑结构动力分析的初始条件,称之为静动力综合分析问题.该分析方法综合考虑了静动荷载对结构地震响应的影响,解决了因静动边界不能共存而只能考虑其中一种边界的问题.静动边界不能共存的原因在于二者边界条件不同,在静力边界中通常侧边界采用滚轴边界、底边界采用固定边界(如图4所示);本文动力边界采用黏弹性人工边界(图1所示).

图4 静力分析边界

因静、动力边界条件不同,若同时考虑会导致结果失真,对结构进行地震响应分析时不能忽略该问题.文章采用一种黏弹性静-动力统一人工边界,该方法可实现静动力综合分析问题中的边界转换,其求解步骤如下:

1)地应力平衡.进行动力分析时,为使重力荷载作用时地基仍保持初始状态,要进行地应力平衡.因此先对结构进行静力分析,即添加静力边界条件和重力荷载,导出地基的应力场.

2)求解支座反力.将上一步导出的应力场作为初始边界条件,施加静力边界条件、重力、水荷载等静力荷载进行求解.边界结点的受力可分解为静力约束对地基的作用和地基对静力边界作用的叠加,如图5所示,最后导出支座水平向反力f1和竖直向反力f2.

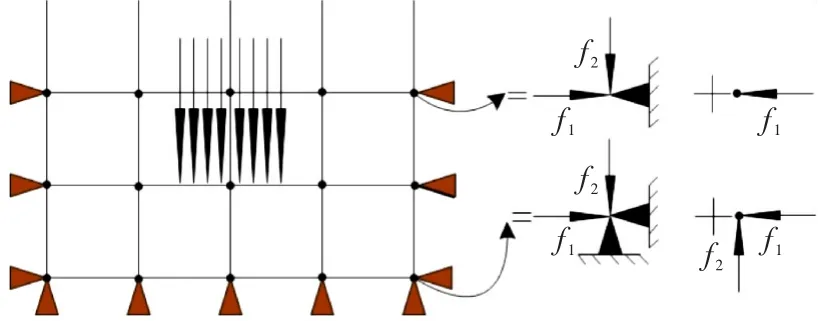
图5 求解支座反力

3)动力分析.将得到的支座反力作为静力约束的等效替代施加于边界,如图6所示.施加动力边界条件(黏弹性边界)以及静力(包含重力荷载、水压力等)、地震荷载等进行动力分析.

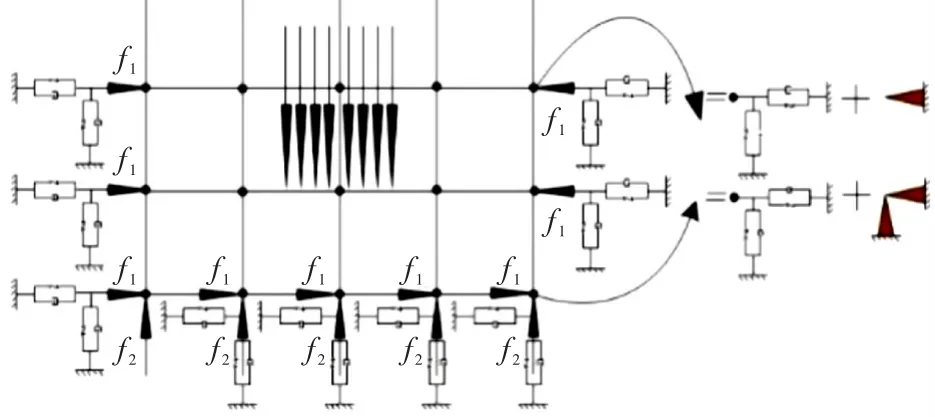
图6 动力人工边界

2 算例验证

为了验证文中波场分解方式下地震动输入方法的计算精度,考虑二维弹性地基模型,将该模型的左、右、底边界全部设置黏弹性边界,上方为半空间自由表面,计算时分别输入入射波角度为0°和30°的P或SV 波.选用动力隐式算法,计算区域大小为700 m×350 m,网格大小取为5 m,时间增量步为0.01 s,计算时长2 s.计算中采用的土体介质参数E=15 GPa,μ=0.24,ρ=2 700 kg/m3,cs=1 496.71 m/s,cp=2 558.93 m/s.入射波位移函数如下:

2.1 P波程序实现与验证

P波在0°、30°斜入射下地表中心点水平或竖直位移时程曲与解析解对比图如图7～8所示.图9～10分别为P波在0°、30°斜入射下不同时刻的波场位移云图.

图7 P波0°斜入射地表中心点位移时程曲线

图8 P波30°斜入射地表中心点位移时程曲线

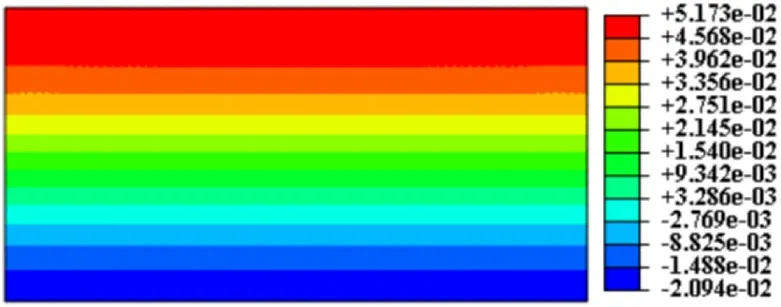
图9 P波0°斜入射位移云图(t=0.3 s)

图10 P波30°斜入射位移云图(t=0.16 s)

2.2 SV波程序实现与验证

SV 波在0°、30°斜入射下地表中心点水平位移时程曲与解析解对比图如图11～12所示.图13～14分别为SV 波在0°、30°斜入射下不同时刻的波场位移云图.

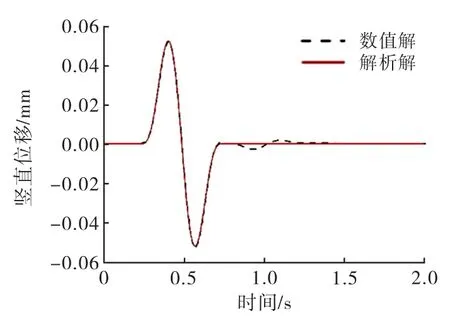
图11 SV 波0°斜入射地表中心点位移时程曲线

图12 SV 波30°斜入射地表中心点位移时程曲线

图13 SV 波0°斜入射位移云图(t=0.27 s)

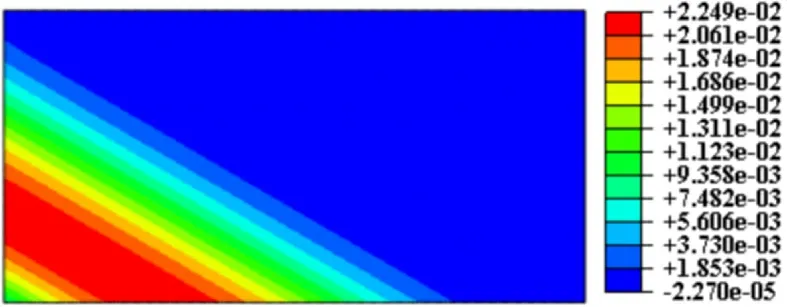
图14 SV 波30°斜入射位移云图(t=0.23 s)

对上述P或SV 波不同斜入射角度位移时程曲线与解析解的对比图与位移云图分析得出:P 或SV波斜入射二维算例计算结果的位移时程曲线与解析解的位移时程曲线吻合良好.所以整体看来本节基于Fortran语言自编的二维P或SV 波斜入射子程序计算结果与解析解基本吻合良好.

3 地震波斜入射作用下混凝土坝地震响应分析

本节基于FORTRAN 语言编写的二维P波斜入射子程序,并利用黄登混凝土重力坝-库水-地基模型进行工程算例分析,因SV 波入射时存在临界角,在此由该工程模型的基本参数及公式(16)可计算得出临界角α1为35.8°.

其中,SV 波临界角的公式为[29]

在此,对于P波斜入射分以0°、5°、10°、15°、20°、25°、30°、45°、60°;对于SV 波斜入射分以0°、5°、10°、15°、20°、25°、30°进行工程算例分析.并对坝体关键点(坝踵、上游折坡处、坝趾)的有限元计算结果进行提取与分析.

3.1 模型参数及作用荷载

3.1.1 模型参数

坝体不模拟分区,只采用一种混凝土材料,并假定为线弹性,动弹模取为静弹模的1.5倍,阻尼比取5%;地基假定为均质线弹性介质,且忽略材料阻尼,材料参数见表1,计算模型如图15所示.

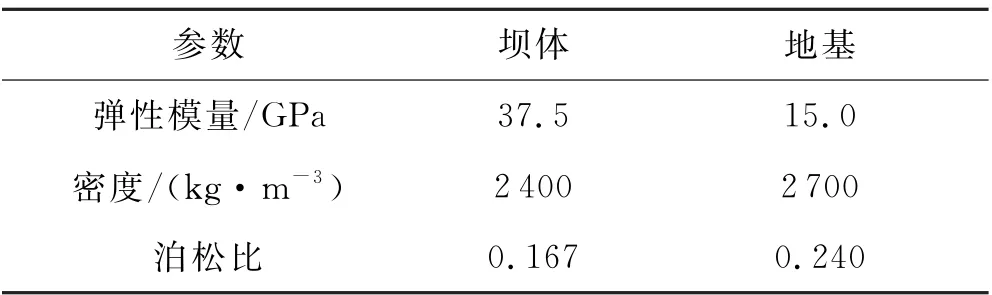
表1 模型材料力学特性参数

图15 重力坝-库水-地基系统计算模型

此外,在实际的动态分析中还考虑了坝体结构的阻尼,本节使用瑞利阻尼的标准形式来计算,即两两参数模型见式[11]:

式中:ω1、ω2分别为坝体-地基结构自振状况下的前两阶模态频率;ξ为阻尼系数,对于重力坝ξ=5%.

3.1.2 作用荷载

本工况选取黄登混凝土重力坝12号挡水坝段,考虑上游正常蓄水位情况进行数值模拟计算,作用荷载如下:

1)自重荷载;

2)静水压力:上游正常蓄水位1 619.00 m,下游尾水位1 422.00 m;

3)动水压力:采用Westergaard公式计算的动水附加质量[7];

4)地震荷载:采用Koyna地震时程,总历时为10 s,选择固定时间步长Δt=0.01 s进行计算.加速度时程如图16所示.

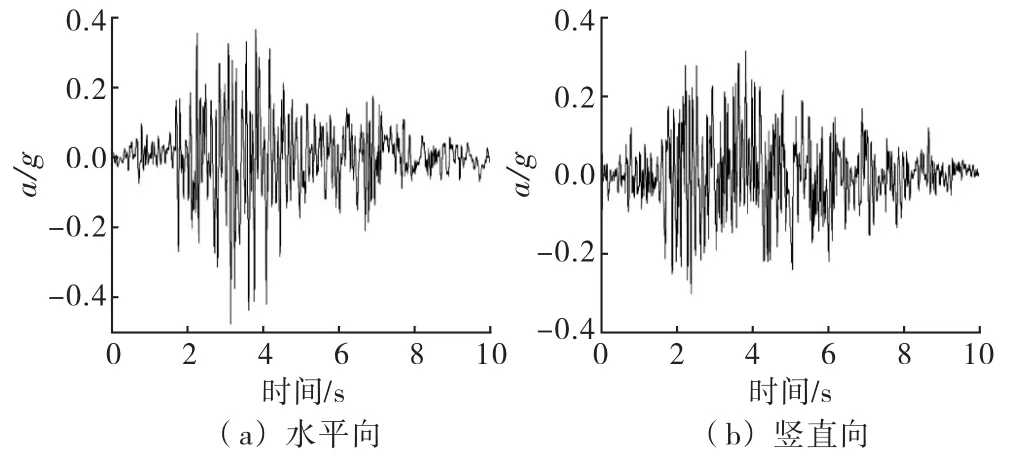
图16 地震动加速度时程曲线

3.2 P波斜入射下坝体动力响应分析

3.2.1 坝体关键点位移响应

如图17为不同P波入射角度的坝顶坝踵点相对位移时程曲线,为了更清晰直观地看出坝顶坝踵点相对位移随着角度增加的变化规律,如图18所示分别提取了不同入射角度的相对位移峰值.从图中可以得出:随着入射角度的增加坝顶坝踵点水平、竖直相对位移时程曲线整体上逐渐增大,其中60°较0°的峰值相对位移,水平向增加了110.11%,竖直向增加了48.52%,这说明P波斜入射在0°～60°内入射角度为60°时斜入射时对地震响应影响较大.

图17 P波斜入射下坝顶坝踵点竖向相对位移曲线

图18 P波斜入射下坝顶坝踵点相对位移峰值曲线

3.2.2 坝体关键点应力响应

图19～20分别为坝踵点、坝趾点两个坝体易损害点的不同入射角度的最大或最小主应力时程曲线,对应分别提取了不同入射角度的关键点主应力峰值如图21～22所示.从图中可以得出:随着入射角度的增加坝踵点、坝趾点的应力时程曲线整体上随着入射角度的增加最大、最小主应力均呈现出逐渐增加的趋势.对比两个关键点不同入射角度的主应力峰值曲线发现随着入射角度的增加峰值应力均逐渐增加,其中坝踵处的峰值应力60°为0°的11.15倍;坝趾处最小主应力增加了10.42%.这说明P 波斜入射在0°～60°内,入射角度为60°时对坝体动力响应的影响程度较大.

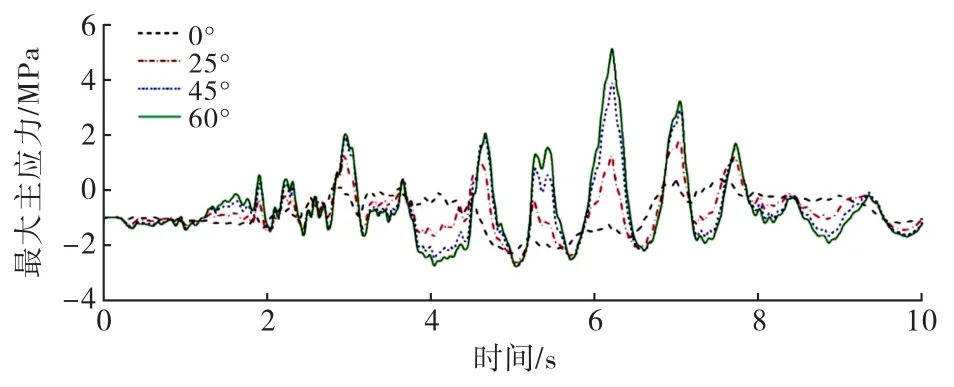
图19 P波斜入射下坝踵最大主应力时程曲线

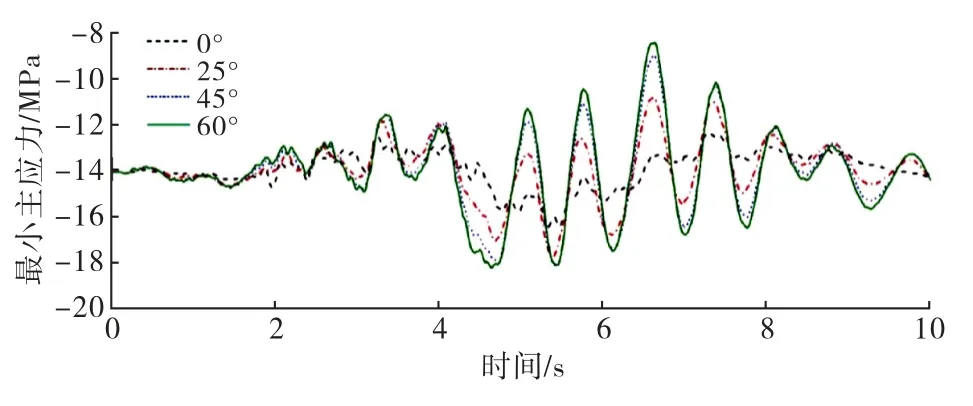
图20 P波斜入射下坝趾最小主应力时程曲线

图21 P波斜入射下坝踵点最大主应力峰值

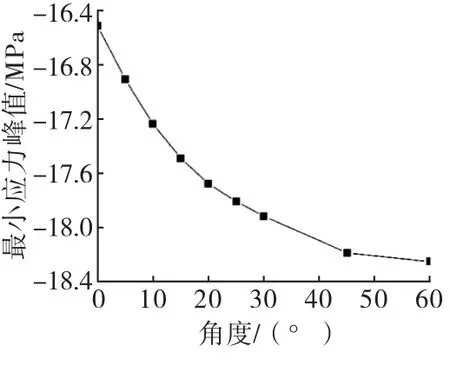
图22 P波斜入射下坝趾最小主应力峰值

3.3 SV波斜入射下坝体动力响应分析

3.3.1 坝体关键点位移响应

图23为SV 波斜入射时,坝体3 个不同入射角度的坝顶坝踵点相对位移时程曲线,因相对位移随着角度的增加变化较为复杂,同时为了更清晰直观地表达坝顶坝踵点相对位移随着SV 波入射角度增加的变化规律,如图24所示提取了不同入射角度的相对位移峰值.对比不同角度的相对位移峰值发现在15°后位移峰值的变化规律出现了不同,整体来看入射角度为0°(即垂直入射)与其他入射角度相比无论是横向还是纵向相对位移是最大的,其中较30°的峰值相对位移,水平向降低2.31%,竖直向降低1.18%,这说明SV 波0°(即垂直入射)入射对地震响应影响变化不大.可以看出:随着入射角度的增加坝顶坝踵点水平、竖直相对位移时程曲线整体上变化不大.

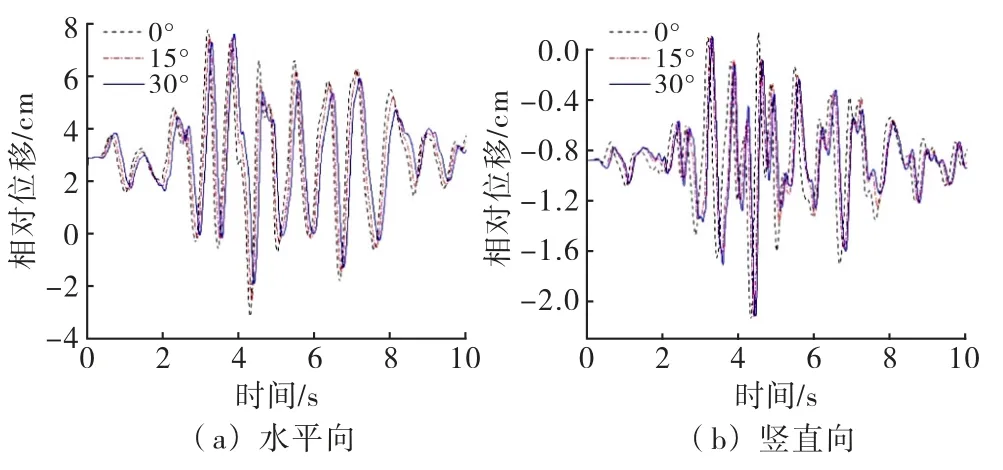
图23 SV 波斜入射下坝顶坝踵点相对位移曲线

图24 SV 波斜入射下坝顶坝踵点相对位移峰值曲线

3.3.2 坝体关键点应力响应

图25～26分别为上游折坡处、坝趾点的不同入射角度的最大或最小主应力时程曲线,为了更清晰直观地看出随着角度增加关键点的主应力变化规律,如图27～28所示,分别提取了不同入射角度的关键点主应力峰值.

图25 SV 波斜入射下上游折坡处最大主应力时程曲线

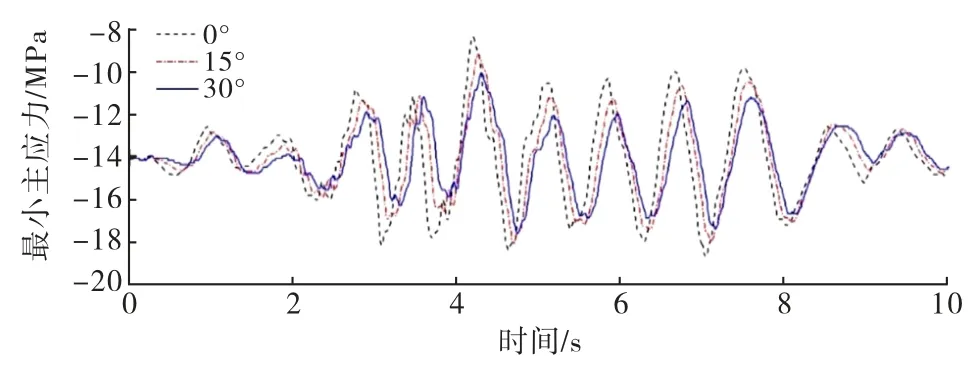
图26 SV 波斜入射下坝趾最小主应力时程曲线

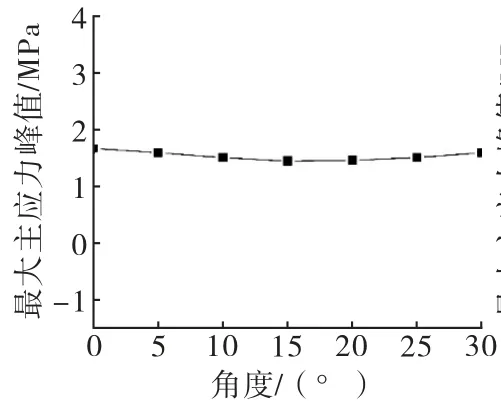
图27 SV 波斜入射下上游折坡处最大主应力峰值

图28 SV 波斜入射下坝趾最小主应力峰值

从图中可以得出:入射角度为0°与其他入射角度相比无论是上游折坡处还是坝趾的主应力都是最大的.其中30°相较0°,上游折坡处最大主应力降低了4.85%,坝趾处最小主应力降低了5.94%.总的来说,对于SV 波斜入射情况下,随着入射角度的增加上游折坡处、坝趾点两个关键点的应力时程曲线整体上影响不大.

4 结 论

以黄登混凝土重力坝为研究对象,基于黏弹性静-动统一人工边界,研究P 波和SV 波在不同斜入射角度下混凝土坝-地基-库水系统的地震响应,得出以下结论:

1)不同地震波斜入射下的动力响应规律与垂直入射相比变化差异较大.P波斜入射时的地震响应规律与垂直入射相比有明显的不同,P波与SV 波斜入射时的地震响应规律也存在差异;在重力坝动力响应分析中很有必要考虑地震波的不同入射角度.

2)P波斜入射时,随着入射角度的增加坝体关键点的水平、竖直相对位移与主应力值逐渐增加,其中30°与0°相比,峰值相对位移水平向增加了110.11%,竖直向增加了48.52%;坝踵处最大拉应力为0°时的11.15倍;坝趾处最小主应力增加了10.42%.这说明P波斜入射在0°～60°,内入射角度为60°时斜入射时坝体的地震响应较大.

3)SV 波斜入射时,随着入射角度的增加坝体关键点的水平、竖直相对位移与主应力值变化不大,虽在15°后位移峰值的变化规律出现了不同,但整体来看入射角度为0°(即垂直入射)与其他入射角度相比无论是水平还是竖直相对位移均是最大的,这说明相较其他角度,SV 波0°入射时坝体的地震响应较大.