基于IEWT-MOMEDA-FSC的滚动轴承故障诊断

吴振雄 王林军 邹腾枭 陈梦华 陈保家

(1.三峡大学 水电机械设备设计与维护湖北省重点实验室, 湖北 宜昌 443002;2.三峡大学 机械与动力学院, 湖北 宜昌 443002;3.湖北特种设备检验检测研究院宜昌分院, 湖北 宜昌 443000)

滚动轴承是旋转机械中的核心部件,它由内圈、外圈、滚动体和支架组成,可用于支撑和传动.由于其长期处于受载状态和恶劣环境[1],无法保证正常工作状态,故需要经常对其进行故障诊断和监测.常用的故障检测技术有信号处理技术、声发射技术、振动分析技术和热成像技术[2]等.声发射技术受环境噪声干扰较大[3],所以,科研人员通常采用振动分析技术来检测轴承,当采用此技术时,通过测量轴承的振动信号,根据振动频谱的特征来识别轴承的故障类型[4].但是测量的故障信号往往伴随各种复杂噪音,使得在提取故障特征时存在一些困难.

针对滚动轴承故障的特征提取问题,常用的方法有经验模态分解(empirical mode decomposition,EMD)、完全噪声辅助聚合经验模态分解(complete ensemble empirical mode decomposition with adaptive noise,CEEMDAN)、变分模态分解(variational mode decomposition,VMD)、经验小波变换(empirical wavelrt transform,EWT)[5].这些方法将原始信号分解为一系列的本征模态分量,再筛选出有效分量进行重构.例如徐洲常等[6]用互相关系数筛选EMD分解出来的IMF 分量,然后通过自相关方法剔除其中的干扰混叠信号,实现了信号的多层降噪.肖俊青等[7]提出用皮尔森相关系数筛选CEEMDAN 的最佳分量组,再将其输入卷积神经网络进行故障诊断.这些方法都能有效地提取出故障信号,但EMD 系列存在着模态混叠问题和端点效应[8],改进方法也没有完全消除其影响,在处理复杂信号时仍会产生虚假分量从而降低分解精度.杨挣鑫等[9]用VMD 分解后进行希尔伯特变换来计算IMF 的瞬时能量矩阵,的确避免了端点效应和虚假分量的问题,但VMD 中核参数和惩罚因子需要人工选择,算法复杂程度高.张震等[10]用相关系数指标判别有效奇异值分解子空间的改进SVD 算法,然后进行快速谱相关分析计算,完整地提取信号的细节特征,但其判别指标太过单一,速度较慢.盛嘉玖等[11]提出了一种基于能量包络趋势线来划分频谱的改进EWT 算法,利用Teager能量算子和希尔伯特变换得到能量包络线,提取极大值平滑处理后进行一阶差分来划分频带,有效缩减了最优共振频带范围,但该方法用于轴承故障诊断还缺少后续降噪处理,仍存在噪声干扰.由于轴承故障特征微弱,在强噪声环境下故障信号会被噪声所淹没,严重影响故障特征提取.

综上所述,为了准确高效地提取信号的故障特征,削弱噪声影响,本文提出一种基于改进EWTMOMEDA 和快速谱相关分析的滚动轴承故障诊断方法.首先,使用快速谱相关分析来增强故障特征频率,降低杂波影响;然后利用得出的增强包络谱代替传统EWT 的傅里叶谱进行频带划分,对信号进行滤波重构;最后用得到的IMF 采用峭度值相关系数筛选准则选取包含有效信息多的分量再进行快速谱相关分析,得到能够表征原始振动信号故障特征的增强包络谱.

1 快速谱相关

快速谱相关(fast spectral correlation,FSC)算法最早是由Antoni等[12]提出,该算法基于短时傅里叶变换,可以在不影响其效率的同时快速地计算谱相关.设x(t n)是一个循环周期信号,它的谱相关为

式中:Fs为采样频率;t n为以采样频率Fs得出的时间点,t n=n/F;R x(t n,τ)为x(t n)的循环自相关函数,τ为 时 延;α为 循 环 频 率;f为 载 波 频 率.

信号x(t n)的短时傅利叶变换为

式中:N w为窗宽;R为移动步长;w[n]为窗函数,是x(t n)的简写;Fs为采样频率;f k为离散频率且f k=kΔf,k=0,…,N w-1;频率分辨率Δf=Fs/N w.

短时傅里叶变换的相位校正函数为

式中:X w(i,f k)为信号x(t n)在iR/Fs时,以f k为中心,Δf为带宽的复合包络;|X w(i,f k)|2为在频

2 EWT原理及其改进

2.1 EWT原理

EWT 是Gilles在2013年提出的一种信号的分解方法[13],它结合了小波变换的完整理论和EMD 多层分解的优势,通过在傅里叶频谱中设置一个小波滤波器来提取信号的不同模式,实现模态分解.EWT 的主要步骤如下:

(1)对信号进行傅里叶变换,并将傅里叶频谱归一化设置在[0,2π]范围内,根据香浓准则,在后续分析过程中只用考虑[0,π]上的信号.

(2)傅里叶的支撑被分为N个区域,如图1 所示,ωn表示每个区域中的边界点,每个部分的频带为Λn=[ωn-1,ωn],过渡区域的宽度为T n=2τn.经验尺度函数和经验小波函数分别为式(11)和式(12).

图1 EWT 边界分割图

重构信号定义为

故经过EWT 所得的本征模态分量f i(t)定义为

2.2 改进EWT的频谱划分方法

在EWT 算法中,划分的边界点依据频谱的极大值点计算得出,但其存在边频带和高幅值位置划分过多导致模态混叠问题,在强噪声环境下还可能出现假的极值点[14].

针对以上频带划分问题,本文提出了快速谱分割方法,具体做法如下:

(1)利用第一节介绍的快速谱相关分析得到的增强包络谱代替傅里叶谱进行频谱边界划分;

(2)将增强包络谱分为N个连续的段落,根据极大值点为中心,概率极小值点为边界划分频段,并将其按照降序排列以构建正交小波滤波器组;

(3)滤波后对划分的每一段信号进行傅里叶逆变换,获得一系列IMFs.

2.3 改进EWT的分量筛选准则

经过改进EWT 分解出来的IMF各个分量都存在不同程度噪声的冲击信号,所以需要根据指标进行筛选.互相关系数表示IMF分量与原信号的相关度,但容易被噪声干扰.峭度值的大小关系着信号的分布密度,但如果分量振幅较大,容易被忽略.文献[15]在通过对原始信号进行CEEMDAN 分解后分别计算每个IMF的相关系数的绝对值和归一化的峭度值,并进行叠加,公式为

式中:Kc为各分量峭度值;K0为原信号峭度值;rc为各分量相关系数的绝对值.

计算原信号峭度值K0和阈值T,相关系数法的阈值计算公式为

定义对比参数C,其公式如下:

为了避免单一筛选准则的片面性,采用峭度与相关系数相结合的复合筛选指标能更好地辨别不同噪声程度的IMF分量,便于提高后续的降噪效果和特征提取能力.

3 MOMEDA降噪

多点最优最小熵解卷积调整(MOMEDA)是MED 和MCKD 的改进方法,克服了参数过多、易受脉冲影响的缺陷.运用非迭代的方式求取最优的有限脉冲响应滤波器,目标函数为

式中:yr为原始冲击信号;f为滤波器向量;目标向量t为解卷积冲击分量的位置和权重.

4 基于IEWT-MOMEDA-FSC 轴承故障诊断

本文将经验小波变换、峭度-相关系数阈值筛选准则、多点最佳最小熵解卷积调整卷积和快速谱增强结合起来,提出了基于EWT-MOMEDA 与快速谱分析的轴承故障诊断方法,具体计算流程如图2所示.

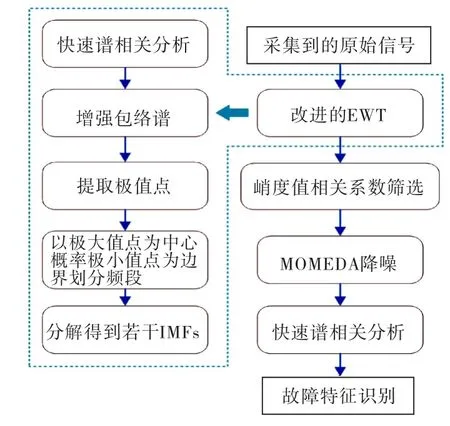
图2 所提方法计算流程图

4.1 实际信号描述

为了验证所提降噪方法的优越性以及对轴承故障诊断的实用价值,本文利用美国凯斯西储大学的公开轴承数据集进行分析验证.轴承实验装置由扭矩传器、1.5 k W 电机、传感器等组成,试验台示意简图如图3所示.轴承类型为6203-2RS深沟球轴承,其参数见表1.

表1 6203-2RS JEM SKF轴承参数

图3 轴承试验台示意简图

故障类型主要是由电火花加工出来的单点损伤,通过安装在感应电动机上的加速度传感器测量出损伤直径为0.177 8 mm,深度为0.279 4 mm.信号采样频率为12 k Hz,电机转速1 772 r/min,数据点数为4 096.

轴承理论故障计算公式为

式中:fi为内圈故障频率;fo为外圈故障频率;r为转速;n为滚珠个数;d为滚珠直径;D为轴承节径;α为接触角.

根据式(26)和(27)计算得出内外圈故障特征频率为159.93 Hz和105.87 Hz,轴承转频为29.53 Hz.

4.2 内圈故障分析

根据图4可知,该信号的时域和频域均包含大量噪声信号,难以判断该轴承的失效形式,需要后续降噪提取故障信号.

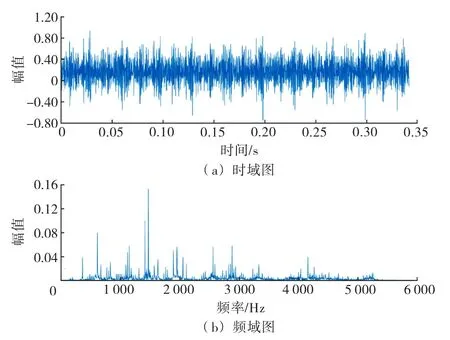
图4 轴承内圈故障时频图

采用本文提出的改进EWT 方法,基于增强包络谱的频谱划分结果如图5(a)所示,EWT 原始频带划分结果如图5(b)所示,通过对比(a)和(b)可知:本文所提频谱划分可以有效地消除小幅分量和相邻多个高幅值分量互相干扰的影响,避免了模态混叠现象;而原始EWT 方法划分的频带过于细密集中,这将影响后续降噪效果.

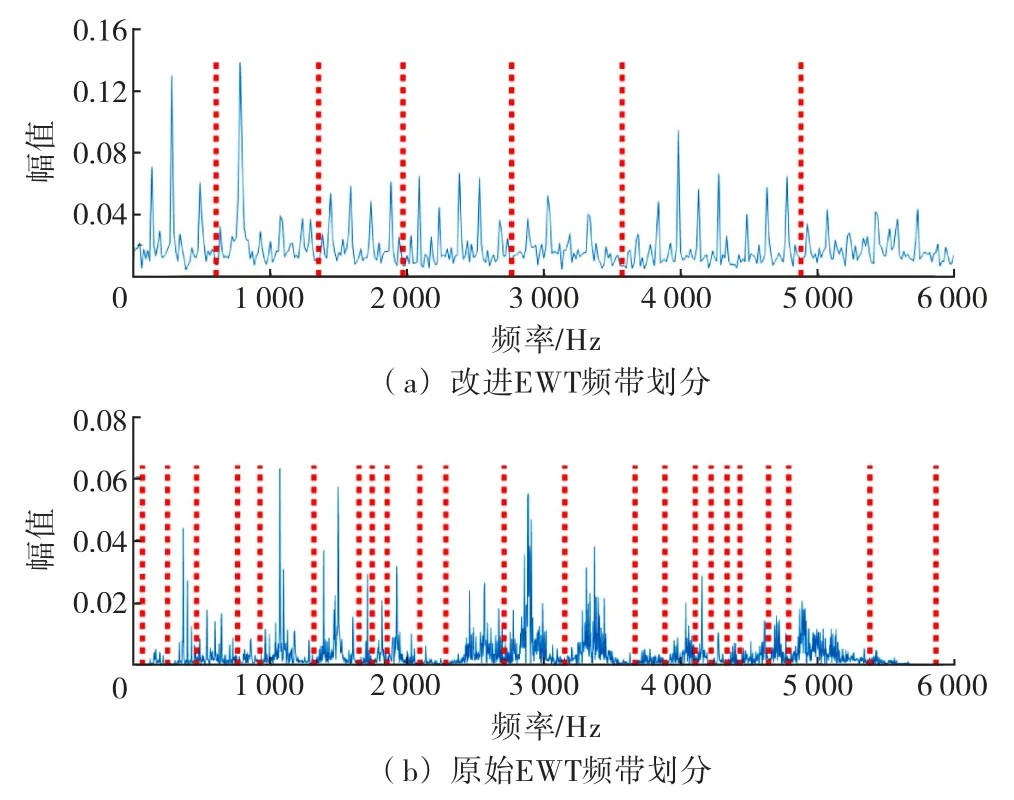
图5 EWT 内圈信号频带划分对比

利用改进的EWT 对信号进行分解得到的IMFs,计算各IMF分量与原信号的相关系数和峭度值,根据式(17)～(19)计算出各个分量的W值和对比参数C,并选取W值大于C的分量进行重构.经过计算得C值为1.165 9,具体参数见表2.

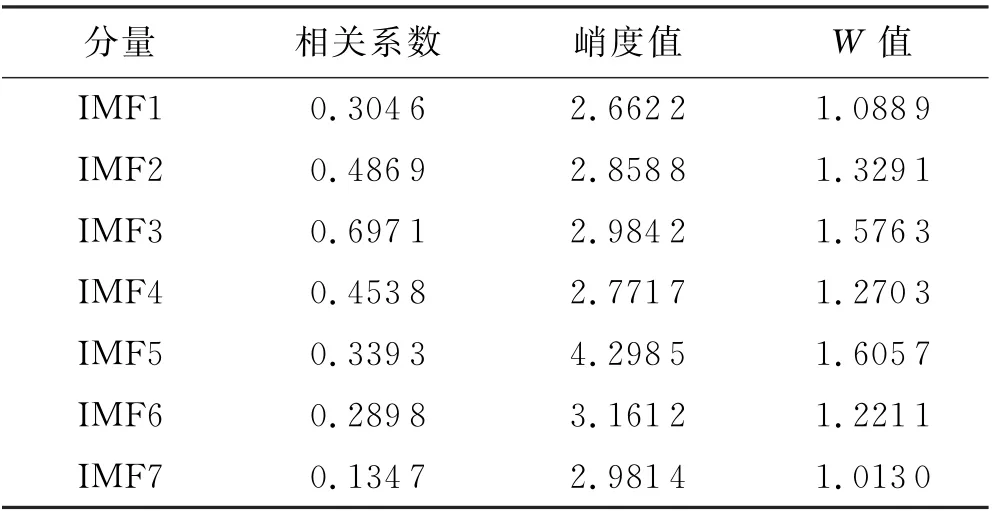
表2 IMFs分量参数

由表2可知,IMF2～IMF6的W值大于阈值C,对这5个分量进行重构,重构信号的时域图和包络谱图如图6～7所示.虽然在包络谱中可以找到故障频率,但其幅值较小,转频以及3倍以上的故障频率仍被噪声遮盖,不能够清晰地表达特征.

图6 内圈重构信号时域图

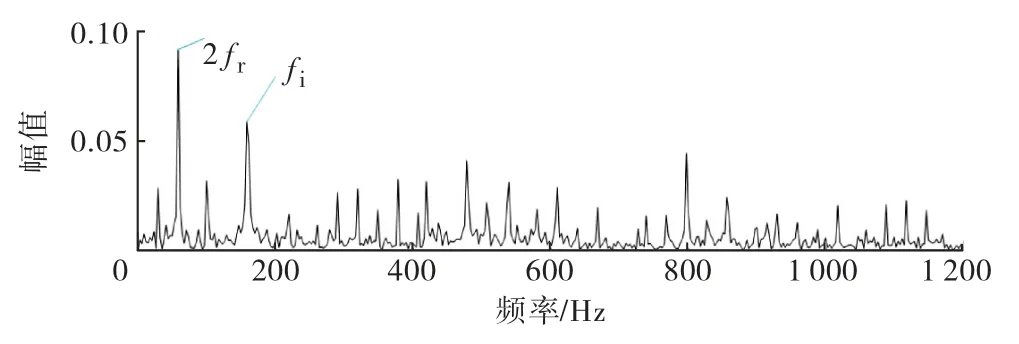
图7 内圈重构信号包络谱

为了使故障信号更加突出,选用MOMEDA 对重构信号进行降噪,根据理论故障频率和采样点数设置周期p为75,结果如图8所示.将降噪后信号进行快速谱相关分析,得出结果如图9所示.

图8 内圈去噪信号时域图

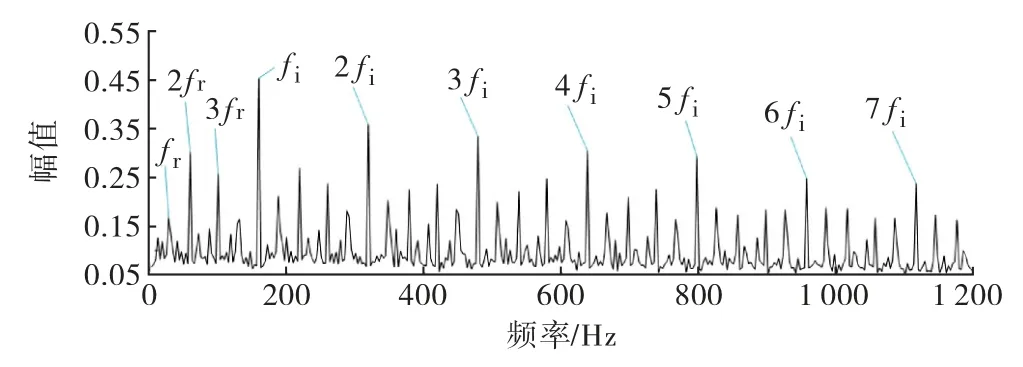
图9 内圈去噪信号增强包络谱

在增强包络谱中可以清晰地看出1～7倍的故障频率以及1～3倍转频,且故障频率为159.58 Hz,与内圈理论故障特征频率基本相同,相对误差仅为0.22%,由此可以准确判断该轴承存在内圈故障.

4.3 外圈故障分析

图10是轴承外圈故障信号时域图和频域图,可以看出含有大量噪声干扰,不能准确提取故障特征.与内圈故障的分析相似,先对原始信号进行改进EWT 分解,划分边界如图11所示.经过峭度-相关系数筛选后将IMF2～IMF6重构得到如图12所示的包络谱,只有1倍故障频率和转频的幅值较大,且仍然存在其他噪声频率干扰.

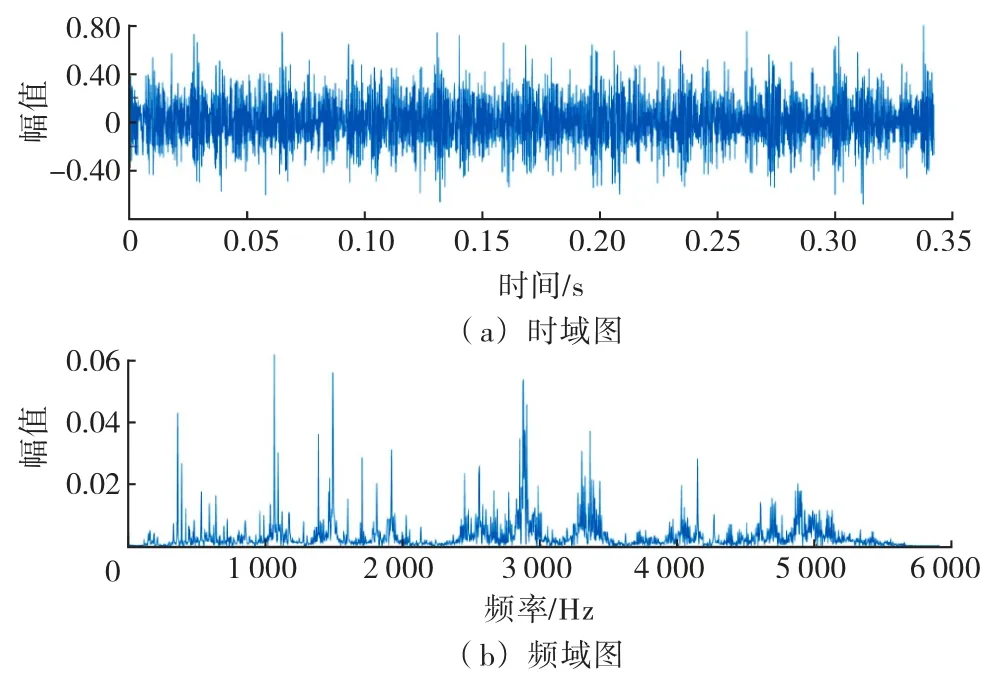
图10 外圈故障信号时频图

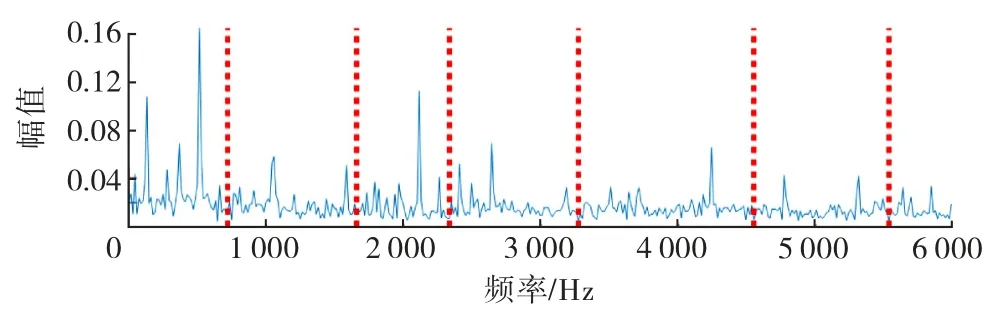
图11 改进EWT 外圈信号频带划分

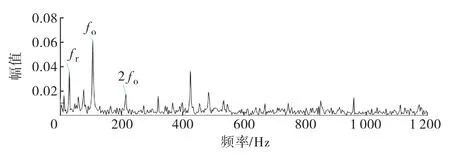
图12 外圈信号降噪后频域图

对重构信号进行MOMEDA 降噪后再经过快速谱相关分析得到增强包络谱,如图13所示.可以明显地看到1～7倍故障频率和1倍转频,且1倍故障频率为106.39 Hz,相对误差为0.46%,小于1%,误差在合理范围之内,由此可以准确判断该轴承出现外圈故障.

图13 外圈去噪信号增强包络谱

5 结 语

本文提出了一种基于改进EWT-MOMEDAFSC的滚动轴承故障特征分析方法,根据实例分析验证与对比分析,可以得出以下结论.

1)通过计算增强包络谱的极值,来设置EWT 的频谱边界,解决了EWT 算法中频谱分割不准确、需要人为设置参数等问题.同时,改进EWT 算法效果更好,能有效避免模态混叠、频带破裂和端点效应.

2)峭度值相关系数筛选准则发挥了多指标的优势,更加全面准确地筛选出了所含有用信息多的分量,避免了单指标只考虑相关度或峭度值时具有的局限性.

3)快速谱相关分析具有较强的适应性和灵活性,处理速度快,且得出的增强包络谱中的循环频率能有效增强故障信号的特征频率,可清晰判断故障类型.