IDDES 方法模拟风切变下大型水平轴风力机流场特性

杨从新，张宇婷，岳念西

（1.兰州理工大学能源与动力工程学院，甘肃 兰州 730050；2.甘肃省流体机械及系统重点实验室,甘肃 兰州 730050）

大气边界层内的气流受地形、地表植物、建筑等障碍物的影响，流速随高度而发生变化，越远离地面流速越大且到达某一高度后保持相对稳定。随着风电机组大型化，轮毂高度和风轮直径越来越大，这种不均匀的剪切流对风力机的影响越来越明显，导致风力发电机组实际输出功率难以达到预期值，而且在风力机后方形成较大的速度损失和复杂的涡结构等；因此，风力机气动性能分析和流场分析很有必要考虑风剪切的影响。目前，已有不少国内外学者用不同方法分析了风力机的气动性能和流场状况。文献[1-5]以小型风力机为研究对象，利用风洞实验测量数据，建立了较详细的风力机气动信息数据库，为分析风力机的流场特征、验证数值模拟方法提供了可靠的依据。文献[6]用BEM 方法和RANS(雷诺平均模拟)方法对飞行器专用风机在高空环境中的气动特性进行了瞬态模拟比较，发现在设计工况下两种方法有较好的一致性。文献[7-8]基于致动线模型结合RANS 方法和LES(大涡模拟)方法模拟小型风力机尾流中的湍流结构，结果发现均匀入流与剪切入流条件下风力机流场的主要区别是尾流场速度亏损的对称性，另外二者在距地面较高处雷诺应力表现出相似性。文献[9]基于致动面模型结合N-S 方程分析了单台Nibe A 型风力机尾流区域内的风速变化、湍流强度、涡结构等。文献[10-11]采用RANS 方法对风力机进行全尺度数值模拟，分析了风切变系数对风力机近尾流区域特性的影响，以及不同叶尖速比下风力机载荷分布和机舱、塔架附近流场结构。以上文献调研可以看出风力机流场分析方法的多样化，其中实验方法是研究风力机空气动力学问题的基础，能比较全面地获取流场信息，促进人类对水平轴风力机流场状态的认知，但其耗时耗力，实现难度较大。致动线、致动面模型结合CFD 方法将风力机简化为线或面，气流经过风力机时无法精确描述叶片表面的流动状态，对流场细节的描述还有待改进。数值模拟中的RANS 方法对定常工况描述具有优势，但风力机运行大多处于非定常状态，显然该方法的计算精度略低。LES 方法计算精度足够高，但它对网格密度要求高、计算量大，已有的研究大多是针对小型风力机。针对以上问题，有人构建RANS-LES 混合模型用于瞬态流动分析，从原始的DES(分离涡模拟)方法到DDES(延迟分离涡模拟)方法再到Spalart 等[12]提出的IDDES 方法，一步步优化改进模拟方法的适用性和精确性。目前，IDDES 方法已被广泛应用于多个领域，比如高速列车气动性能分析[13]、氢燃料燃烧模拟[14]、水泵内部流动分析[15]以及海上垂直轴风力机[16]的空气动力学问题等，以上研究充分发挥了IDDES 方法在解决机械运动非定常问题的适用性和精确度。鉴于此，本文采用高精度的IDDES 方法，分析风切变来流条件下大型水平轴风力机流场特征。

1 计算模型

1.1 几何模型

选择NH 1 500 kW 风力机作为计算模型，风力机的具体参数见表1。对模型进行简化，忽略风轮的锥角和仰角，该风力机的几何模型如图1 所示。

图1 风力机几何模型Fig.1 Geometric model of wind turbine

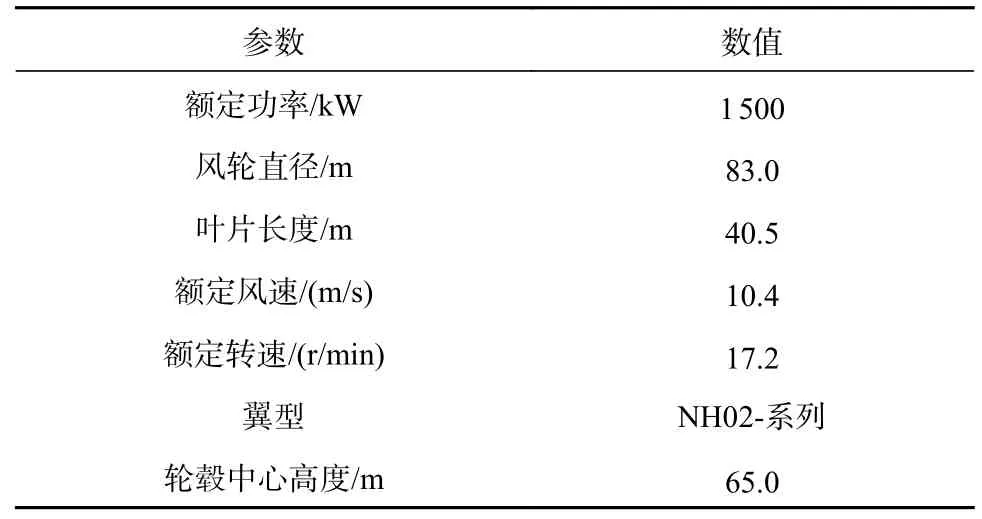
表1 NH 1 500 kW 风力机参数Tab.1 NH 1 500 kW Wind turbine parameters

1.2 数学模型

1.2.1 数值方法

IDDES 方法结合壁面边界层区域附近的雷诺时均模拟和非稳定分离区域大涡模拟的特性。计算流动问题过程中用到的三维不可压缩流体的N-S 方程结合IDDES 方法得到新的湍流输运方程式为：

式中：Pk为由于黏性力引起的湍流生成项；μt为湍流黏度。μt定义为

IDDES 方法湍流长度尺度lIDDES定义为

式中：β*为经验系数，取值0.09；F1为混合函数；CDES1与CDES2为通过混合函数计算的模型系数，分别取值0.78 和0.61；Δ为网格尺度，表达式为

式中：dw为计算点到壁面的距离；hmax为单元最大边长；hwn为垂直于壁面方向的网格尺度。上述IDDES 方法引入lIDDES较好地解决了非定常来流的适用性问题，从而更精确地预测瞬态流动湍动能运输及耗散情况。

1.2.2 风速沿高度方向的指数律分布

用指数律描述风速沿高度变化规律的分布函数表达式为

式中：V为距离地面高度H处的风速大小，m/s；V0为距离地面参考高度H0处 的风速大小，m/s；α为风剪切指数。本文中H0取轮毂中心高度65 m，V0取额定风速10.4 m/s，α取0.16。

1.3 计算域的划分

风力机的计算域由图2 所示的旋转域和静止域两部分组成，原点位于风轮中心，来流速度垂直于XZ平面指向Y轴负方向，计算域入口距离风力机2D(D为风轮直径)，出口距离风力机5D，左右边界距离风轮中心各1D。对计算域进行结构化网格划分，其中旋转域内叶片表面和边界层网格作加密处理，网格加密的局部放大如图3 所示。

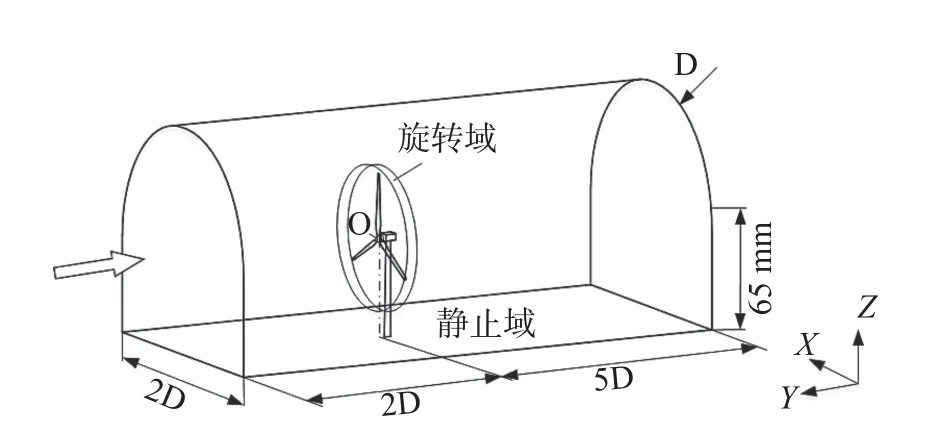
图2 计算域划分示意图Fig.2 Computational domain partition diagram

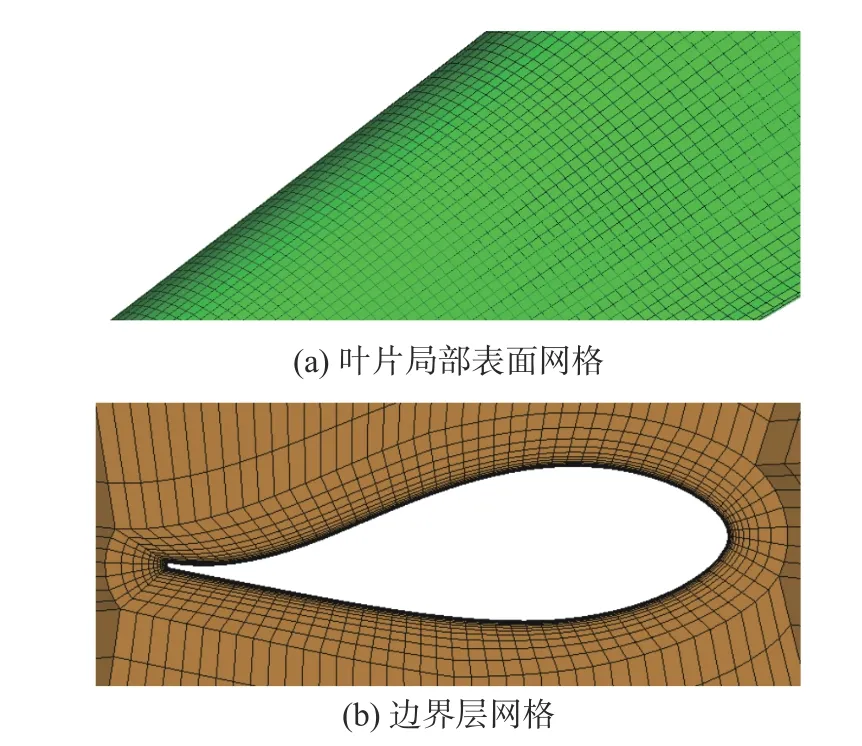
图3 旋转域网格加密局部放大图Fig.3 Local magnification of rotating domain dense mesh

1.4 边界条件及求解器设置

进口边界条件选择速度入口(velocity inlet)，使用用户自定义函数(user defined functions，简称UDF)改变风速在高度方向上的变化，实现剪切入流方式；出口边界条件选择自由出流(outflow)；壁面边界条件为风力机塔筒和机舱设置为无滑移壁面(no slipping wall)，轮毂和叶片设置为旋转壁面(moving wall)。求解器选择压力求解器，采用SIMPLEC 算法实现压力和速度的耦合。二阶迎风格式离散方程，先用RANS 方法计算稳态，待结果收敛后以该结果作为IDDES 方法瞬态计算的初始状态。由风力机额定转速17.2 r/min 计算风轮旋转1°所需时间为0.009 689 9 s，即为瞬态计算的时间步长。监测残差收敛曲线，当达到设置的收敛标准并且其余监测量稳定变化时，可认为计算结果收敛。

2 计算验证

2.1 网格无关性验证

数值模拟中网格密度对计算结果的准确性影响很大，所以做网格无关性验证排除网格密度对结果的干扰。图4 给出了额定风速10.4 m/s 下由不同网格数目计算得到的风力机输出功率以及相对误差大小。由图可知，网格数目越多，风力机的输出功率越大，同时越接近额定功率。当网格数目约2 500 万时，相对误差在5%以内，再加密网格相对误差越来越小。综合考虑计算时长、计算资源、计算误差等因素，选定3 200 万网格数目的数值模拟结果进行分析。

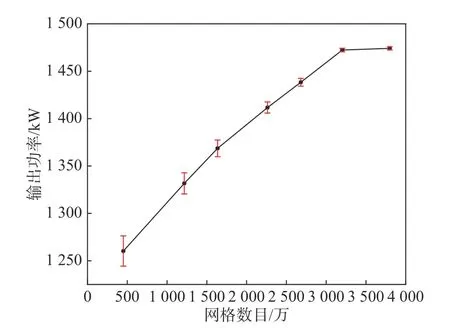
图4 不同网格数下机组输出功率Fig.4 The output power of wind turbine under different mesh number

2.2 准确性验证

为了验证湍流模型的准确性，将额定风速下模拟得到的推力系数CT、转矩系数CM与文献[18]中商用软件GH Bladed 校核结果作对比，结果如表2所示。从表中可以看出IDDES 方法计算结果稍大于GH Bladed 校核结果，推力系数和转矩系数的相对误差分别为6.34%和3.2%，均在10%以内，由此证明IDDES 方法模拟风力机气动性能可靠性较高。

表2 风力机推力、转矩系数对比Tab.2 Comparison of wind turbine thrust and torque coefficients

2.3 数值方法对比验证

从两种模拟方法的瞬时速度云图（图5）对比可以看出，RANS 方法模拟得到的流场在风轮正对高度处速度云图基本呈对称状，而IDDES 方法模拟的流场波动性更强，能捕捉到流场中叶尖涡、叶片尾缘涡和中心涡以及大面积不规则的速度亏损，这种现象更符合风力机真实流场状况，由此可见IDDES 方法在模拟流场细节方面的优势远大于RANS 方法。

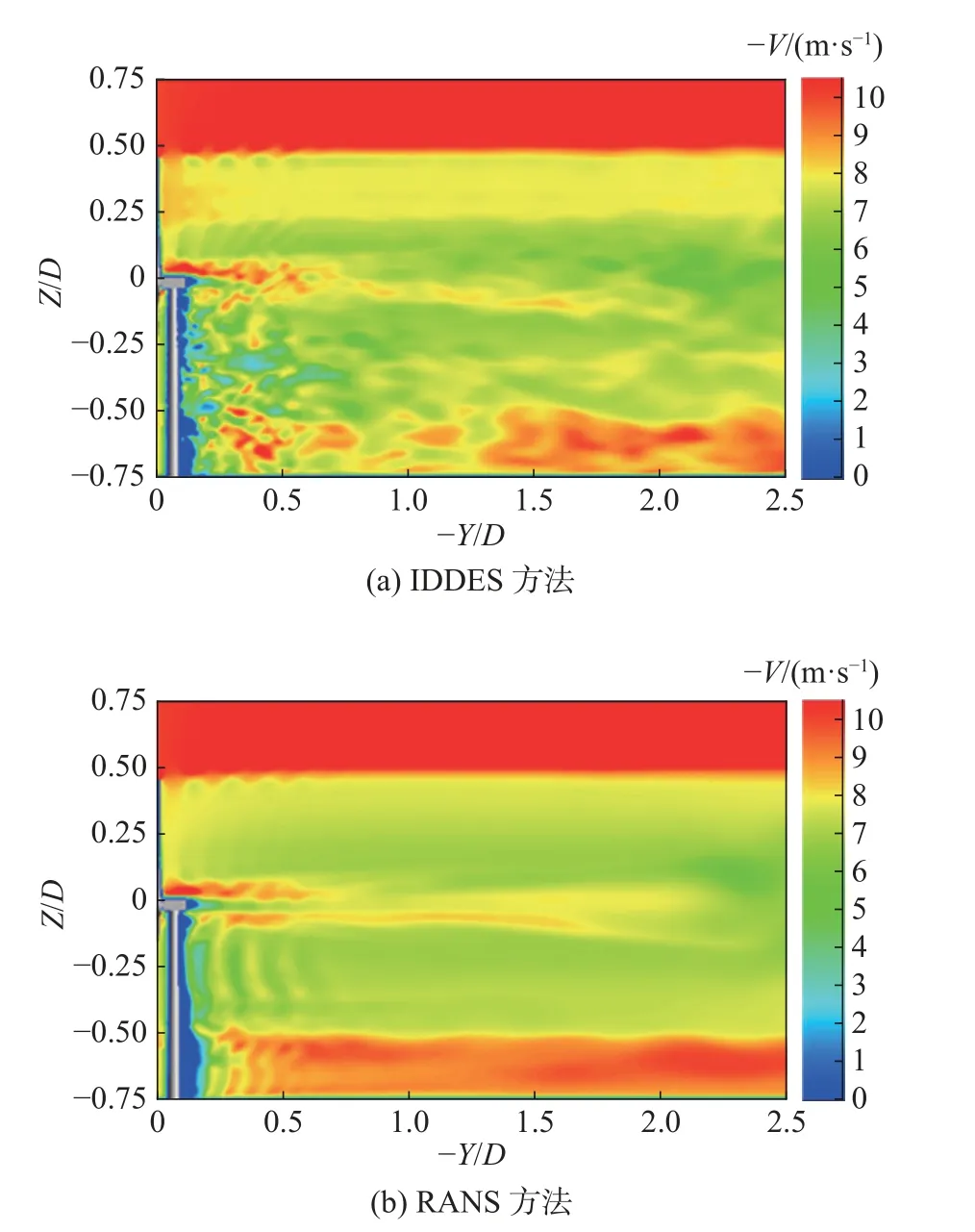
图5 YZ 平面(X=0)瞬时速度云图Fig.5 YZ plane(X=0) instantaneous velocity contour plots

3 计算结果与分析

为了描述方便，定义风轮旋转方位角，图6 为风轮旋转方位角示意图。坐标原点位于风轮中心，当图中1#叶片与X轴垂直并指向Z轴正方向时的方位角记为0°，该叶片绕轴顺时针(风力机正前方视角)旋转一周记为风轮的一个旋转周期，需要3.488 364 s。

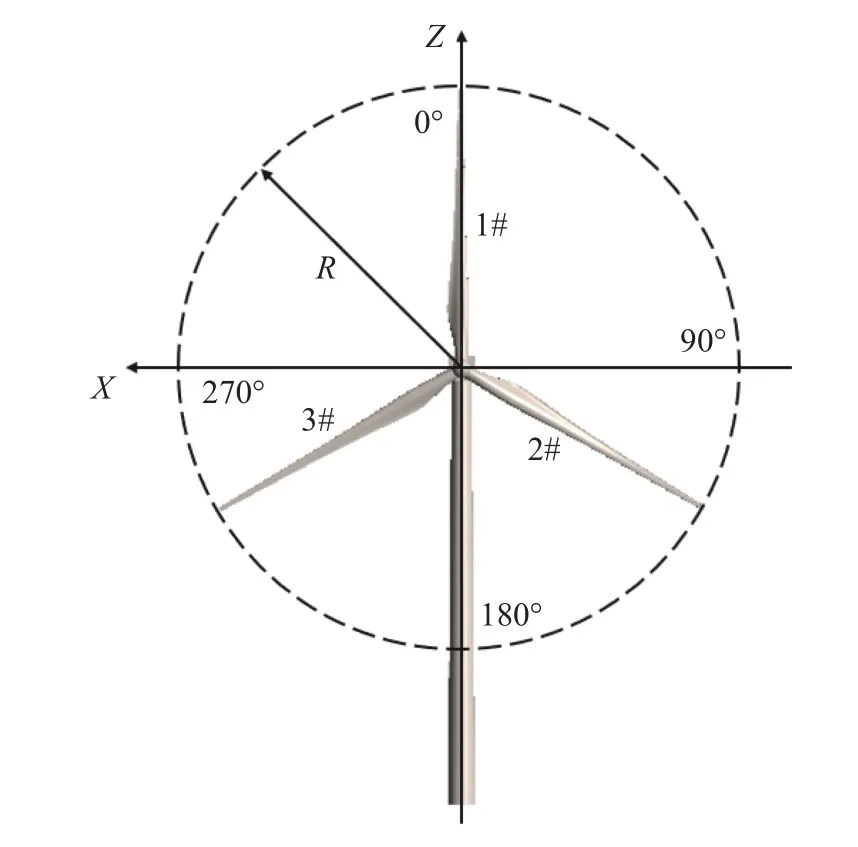
图6 风轮旋转方位角示意图Fig.6 Wind wheel rotation azimuth diagram

3.1 流场速度

速度是描述流场特性的一个重要物理量，流场中任意点的速度可以分解为直角坐标系3 个方向上的速度分量。图7 给出了风轮旋转9 周到达0°方位角时流场中速度分量随高度的变化情况。沿轴向在风力机前后共选取了9 个位置，Z/R=0 对应风轮中心位置，Z/R=±1 对应风轮旋转上下边界。

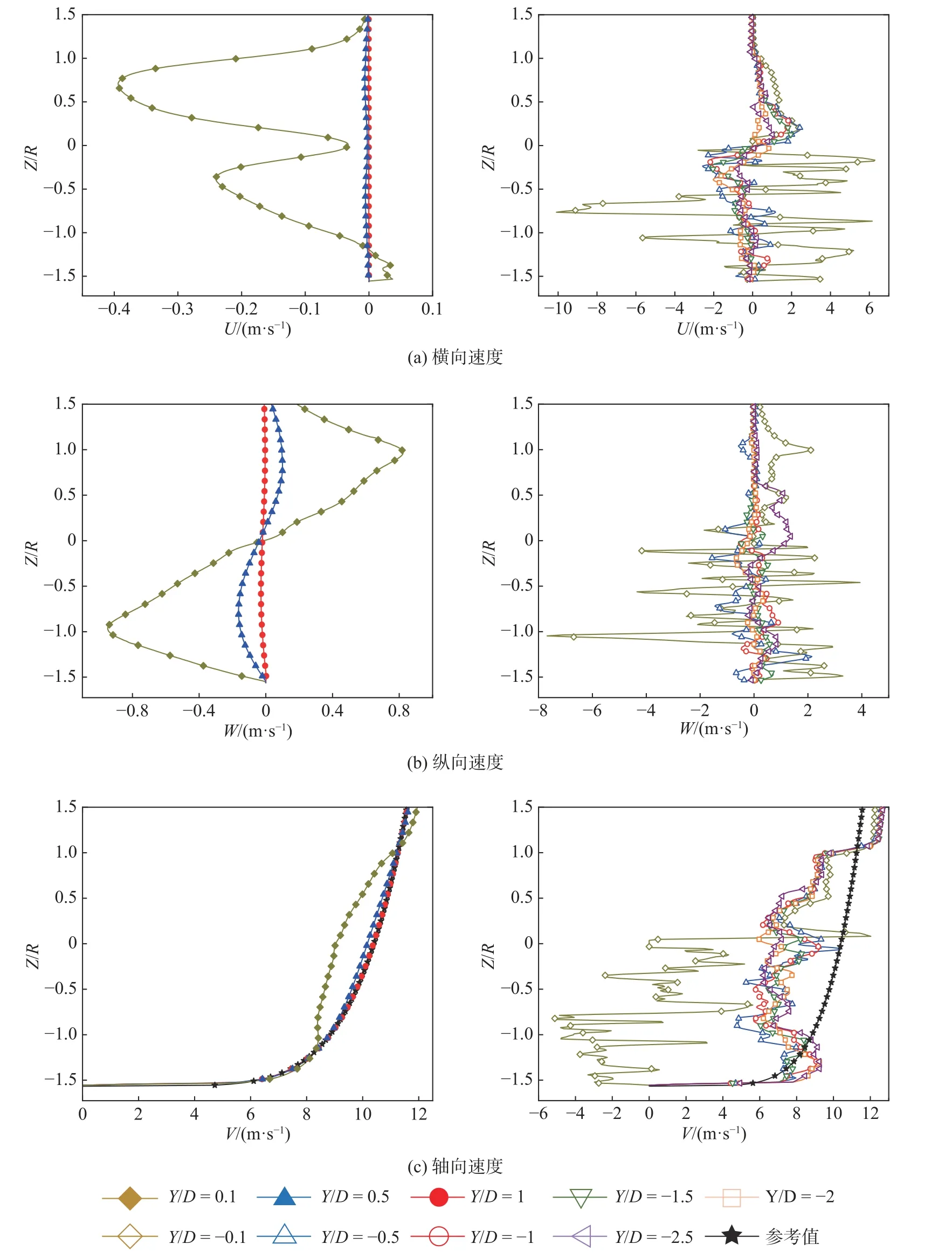
图7 0°方位角风力机YZ 平面(X=0)速度分量分布Fig.7 Velocity component distribution in YZ plane(X=0) of wind turbine at 0° azimuth

从图7 可以看出：风力机前后方的速度变化差异很大，前方1D和0.5D处的横向速度和纵向速度沿高度方向变化量均很小，轴向速度沿高度方向的分布与计算域入口设置的剪切入流曲线几乎重合，说明前方1D和0.5D范围内风力机对气流流速的影响特别小，基本可以忽略；0.1D处3 种速度较另外两处变化幅度变大，横向速度沿高度方向的变化呈现“W”型，平均增长15.3%，最大增长39.4%，风轮中心下方的变化幅度小于上方，纵向速度沿高度方向的变化曲线大致呈对称状，平均增长4.5%，最大增长94.8%，轴向速度在正对风轮位置处小于来流设定值，而在风轮上方略大于来流设定值，平均亏损率为6%，说明风轮的旋转效应对机组前方0.1D处的气流造成扰动。

在风力机后方同一轴向位置处由于组成叶片翼型的气动特性和翼型所处位置的旋转线速度不同，所以速度分量沿高度方向发生不同程度的变化，后方0.1D处3 种速度分量变化最明显，尤其在风轮中心下方(Z/R<0)，由于该位置位于塔筒正后方且距离塔筒很近，受到风轮旋转和塔影效应的综合影响，导致该位置处的速度波动极大，下游处风轮中心下方的速度波动程度大于上方。其主要是因为塔筒后方形成一系列涡结构向下游发展，导致速度波动明显，轴向速度分量在经过风轮之后，后方的速度大小明显低于来流，表现出较强的尾流速度亏损，越靠近风力机位置，亏损越明显，轴向速度分量在风轮后发生亏损用于气流静压的恢复，由此形成尾流效应。在风轮旋转边界上方，轴向速度分量出现加速现象，主要是由于旋转的风轮对叶尖处气流的挤压作用使得该区域的湍流发展充分，气流流动速度加快。

总的来说，由于IDDES 方法在模拟瞬态流场方面有很强的优势，所以用这种方法模拟得到的流场速度波动性较强。越靠近风力机，速度变化越明显，横向速度分量与纵向速度分量都变大，而轴向速度分量相较于来流会减小。原因是气流经过风轮旋转平面时，由于旋转平面的诱导作用使得气流速度在轴向方向发生亏损，轴向速度在风轮前发生亏损用于提高气流静压推动风轮转动作功，轴向速度分量在风轮后发生亏损用于气流静压的恢复，由此形成尾流效应。

3.2 脉动速度频谱分析

为了描述风轮旋转时流场的运动特性，选3 个典型高度(Z=41.5、0、-41.5 m)处风力机前后方不同位置(图8(a))的瞬时风速在4 个旋转周期(17.44182～31.395 276 s) 内的时域变化，监测结果如图8(b)所示。

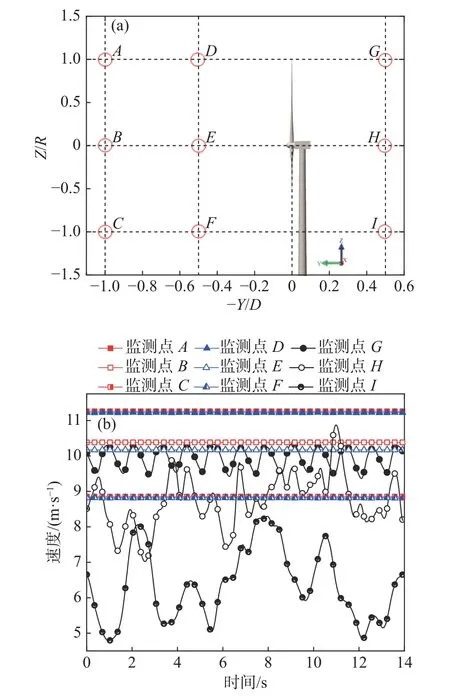
图8 流场监测点分布(a)与监测点速度(b)Fig.8 Monitoring point distribution(a) and velocity(b) in flow field

风力机前方的速度变化较平稳，后方速度波动明显，41.5 m 高度处的速度波动呈现周期性，而0 m高度处受风轮旋转产生中心涡和-41.5 m 高度处受叶片叶尖涡与塔筒的塔影效应综合影响使得速度变化不存在周期性。用脉动风速进行快速傅里叶变换来描述监测点的湍流功率谱特性，脉动风速的功率谱结果如图9 所示。由风力机额定转速n=17.2 r/min 计算可得风轮转频fn为0.286 7 Hz，风轮旋转一周，叶片通过的频率fp为3 倍的风轮转频，即0.86 Hz。从图9 可以看出：风轮前的脉动风速功率谱在任意高度处都存在明显波峰，对应频率均在fp的整数倍处，风轮后的脉动风速功率谱只在41.5 m 高度处有显著波峰，0 与-41.5 m 高度处的监测点处存在的大尺度旋涡影响了功率谱的谱峰分布；速度波动程度越大对应功率谱密度越大，湍动能越大，具体表现为越靠近风力机脉动速度的功率谱密度越大；风轮前的功率谱密度比风轮后方的低，对比风轮后方0.5D距离处功率谱沿高度方向的变化发现，Z=0 高度的脉动速度功率谱密度最大，说明中心涡对功率谱密度的影响最明显。

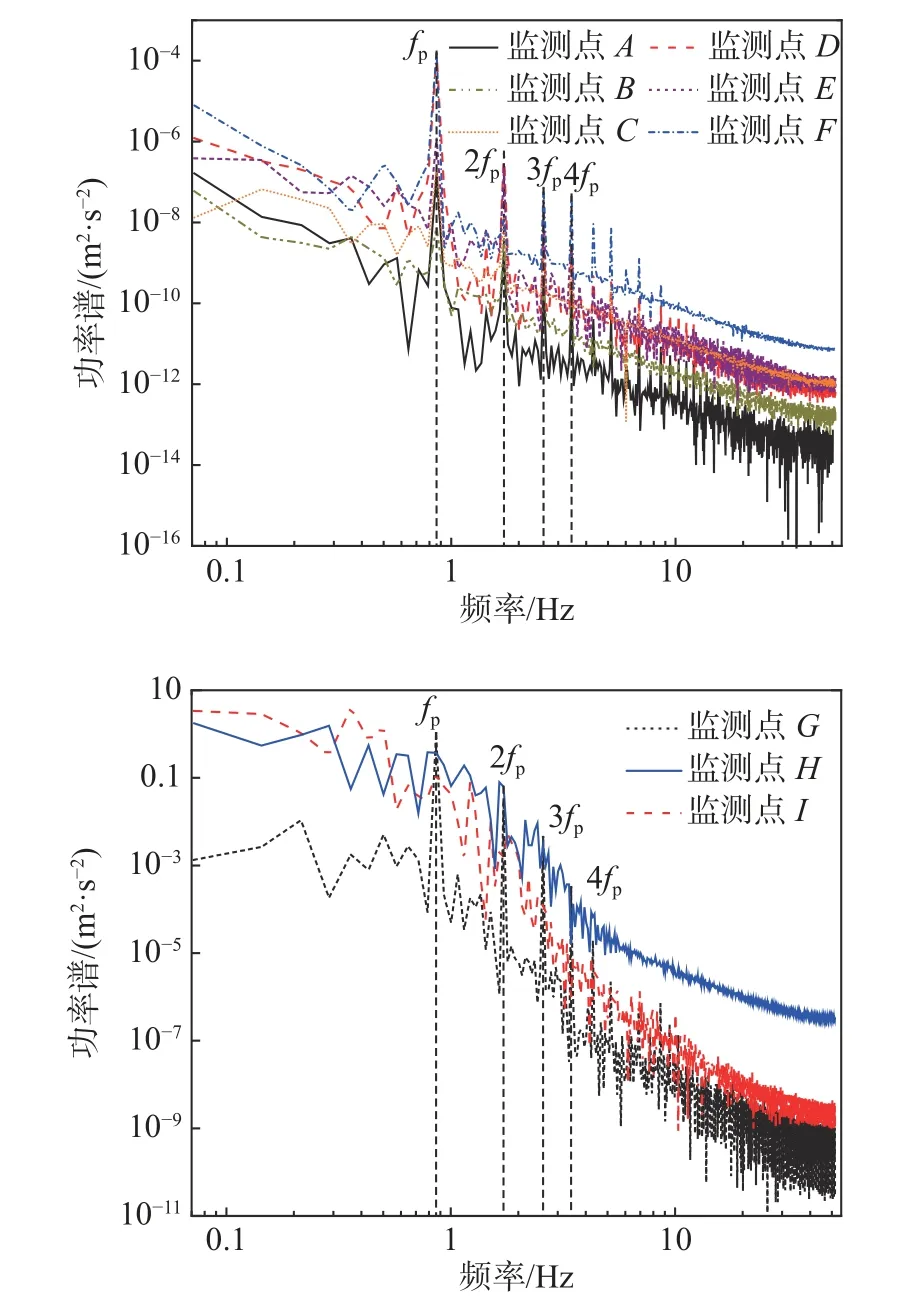
图9 脉动风速的功率谱Fig.9 Power spectrum of fluctuating wind velocity

3.3 输出功率分析

来流条件的不稳定决定了风力机的输出功率会随时间不断发生变化，但这种变化并不是毫无规律的。对比分析一个旋转周期内剪切入流和均匀入流条件下的输出功率随方位角波动情况，结果如图10 所示。由图可以看出两种入流条件下功率输出都呈现余弦变化，在1#叶片的方位角分别处于60°、180°、300°时输出功率出现极小值，此时均匀入流和剪切入流条件下的输出功率分别只有额定功率的95.6%和94.1%。这是因为此时3 支叶片正分别经过塔筒正前方，绕叶片流动的气流与绕塔筒流动的气流相互掺杂影响了风力机气动力的产生，总的来看均匀流下的输出功率大于剪切流。该段时间内均匀流和剪切流的平均输出功率分别为1 510 kW 和1 490.425 kW，风能利用系数分别为0.426 和0.421。为了比较两种入流条件下风力机输出功率的功率谱，选定风轮4 个旋转周期内的转矩数据作为样本，采样时间间隔为0.009 689 9 s，即风轮旋转1°采样一次，得到风轮转矩随时间波动如图11 所示。由图可以看出风轮转矩呈现出脉动特性，在采集样本期间出现了12 个极小值，正好对应每个叶片经过塔筒正前方，说明塔筒的绕流效应会影响风轮的受力状况。

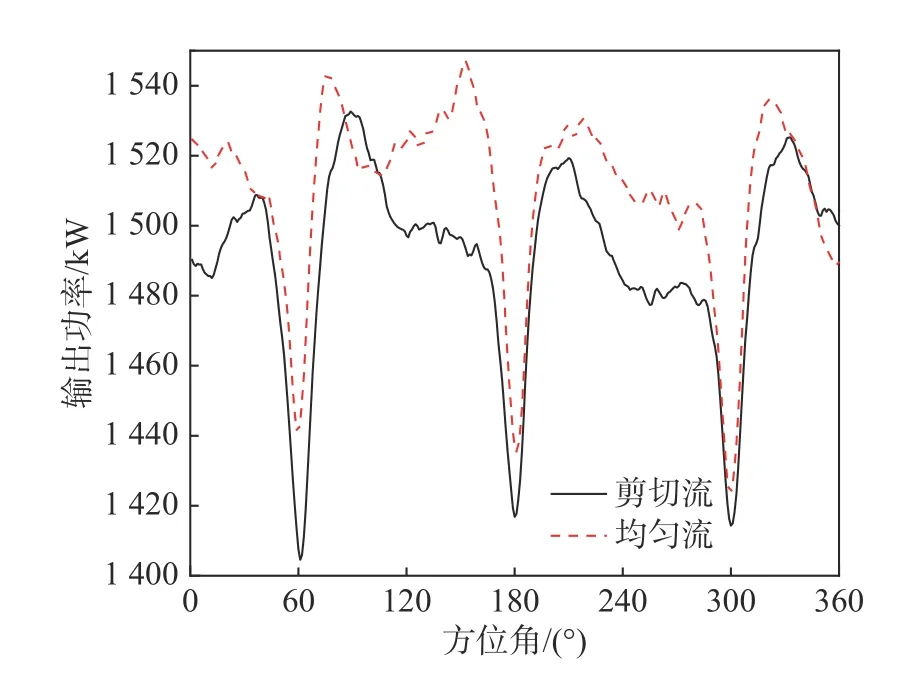
图10 输出功率随方位角的变化Fig.10 Variation of output power with azimuth angle

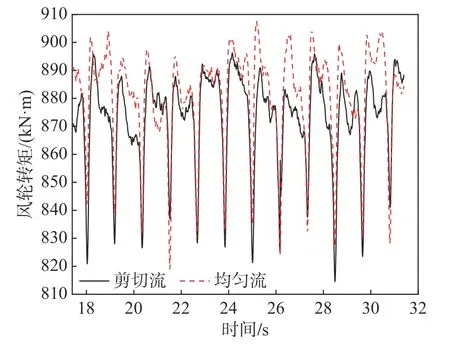
图11 4 个旋转周期内风轮转矩变化Fig.11 The torque of the wind wheel during four rotation cycles

为了反映风力机流场能量输运规律，图12 给出了两种入流情况下的功率谱密度。由图可以观察到两种情况具有相近的频谱变化，功率谱密度随着频率的增大而减小。气流受风轮旋转扰动以及剪切风速的不均匀性影响，流场内的湍流充分发展，其能量谱分为含能区、惯性子区和耗散区3 个部分。其中，含能区生成的大尺度旋涡含有湍动能的绝大部分能量，在惯性子区大尺度旋涡输出能量扩散成众多靠惯性输入能量的小尺度旋涡，并伴随着湍动能逐级连续传递，呈现常见的-5/3 衰减斜率，最终旋涡尺度太小且受流体黏滞力的影响能量损失不断增大，在耗散区湍流能量耗散消失。

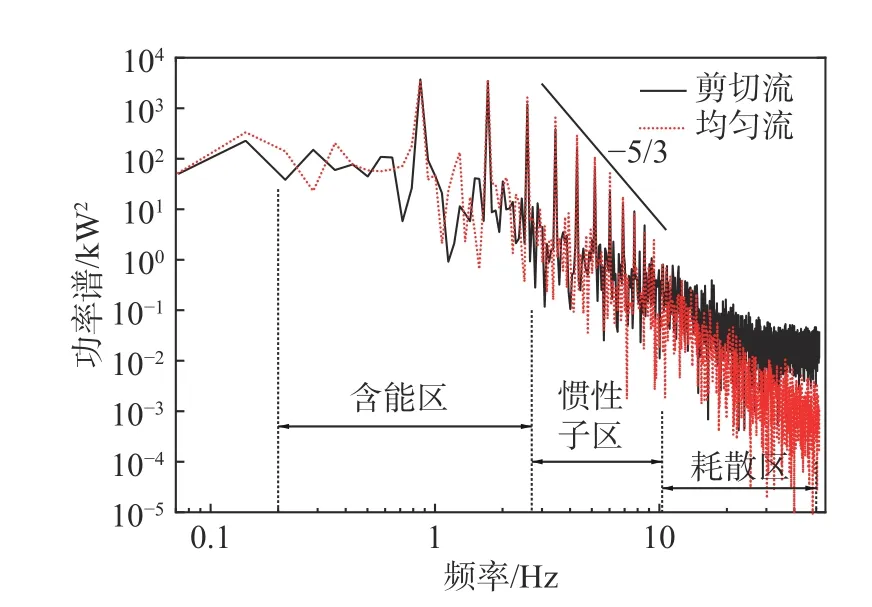
图12 输出功率的频谱特性Fig.12 Frequency spectrum characteristic of output power

4 结论

本文通过IDDES 方法模拟大型风力机运行的流场特性，得出以下结论。

1)在风力机前方，风轮旋转对气流造成的扰动沿高度方向分布比较规律，其中横向速度分量和纵向速度分量都大于入口设定值且呈对称分布，轴向速度分量在风轮旋转平面高度内相较于入口设定变小而在旋转边界以外会增大。在风力机前方速度亏损提高气流静压推动风轮旋转做功，后方流场中出现速度亏损用于恢复气流静压。

2)风力机前方流场内的速度随时间变化较平稳，后方速度呈现明显的脉动特性且离地面越近变化幅度越大。脉动风速的频谱图显示低频区谱峰的出现时刻与叶片转频的整数倍有关，速度波动越大对应的功率谱密度越大。

3)风力机的输出功率呈余弦变化，风切变的存在使得叶片表面受力不均匀从而机组功率和风轮载荷高度波动，在三支叶片分别经过塔筒正前方时出现极小值。同样条件下均匀流的输出功率大于剪切流，两种入流方式的能量变化趋势一致。在含能区大尺度旋涡含有大量湍动能，在惯性子区大尺度旋涡输出能量扩散成小尺度旋涡并满足-5/3 衰减斜率，在耗散区小尺度旋涡受黏滞力影响湍动能耗散消失。

本文总结了剪切入流条件下大型水平轴风力机的流场和功率特性，充分验证了高精度的IDDES方法模拟计算大型水平轴风力机的可行性，为未来该方法应用于更加复杂的流动条件提供参考。