基于振动信号的滚动轴承复合故障诊断研究综述

杨 岗，徐五一，邓 琴，卫昱乾，李 芾

（1.西南交通大学机械工程学院,四川 成都 610036；2.西南交通大学唐山研究院,河北 唐山 063000）

随着旋转机械设备的精密化和复杂度的提高，对设备的运行可靠性提出了更严苛的要求。由于旋转机械设备运行工况复杂及环境恶劣，其零部件极易受到损坏。在实际工况中，任何微小的故障都有可能引起零部件或整机的故障，甚至可能导致毁灭性的损坏和灾难性的事故[1]。因此，有效、快速、准确地评估和识别旋转机械设备的健康状态，对提高其安全性和可靠性至关重要。

作为旋转机械的关键部件，滚动轴承的工作可靠性将直接影响整个设备的精度和寿命[2]。轴承缺陷会导致旋转机械设备处于一种非正常的运行状态，将产生一系列振动冲击和冲击衰减响应，采集到的轴承振动信号也会表现出某种程度的非平稳性和周期性冲击特征[3-4]。因此，工程实际中常通过信号处理方法对滚动轴承振动信号进行故障特征成分的识别和提取，从而达到对轴承运行状态监测和故障诊断的目的[5]。滚动轴承故障类型包括单故障和复合故障。在实际工程中，单故障的发生常会诱发其他故障或多个故障并发，形成所谓的复合故障。复合故障会引发振动之间相互干扰、相互耦合，使得滚动轴承的故障特征提取变得更加困难，一般情况下，用来判断单故障的方法无法准确地识别复合故障。

目前，轴承复合故障诊断领域在故障特征增强、提取、识别、分类和量化等方面取得了众多研究成果。本文对滚动轴承复合故障诊断方法进行综述性研究，总结了目前主要的复合故障诊断原理、算法流程、算法优缺点与应用现状，并对其研究远景进行展望。

1 轴承故障诊断机制及频率特性

滚动轴承的故障形式分为两类：表面损伤和局部磨损[6]。后者属于渐进性故障，危害远小于表面损伤，因此，轴承故障诊断的重点是表面损伤类故障。当轴承表面产生缺陷时，各组件之间相互作用，会产生冲击。根据冲击振动的性质，可将其分为2 类[7]：1）故障部位与正常部件表面碰撞而产生的周期性低频振动冲击；2）轴承表面瞬时断裂或第一类冲击导致的系统固有高频振动冲击。前一类振动冲击信号的发生频率即为需要提取的轴承故障特征频率。然而，受到背景噪声和传递路径等因素的影响，除故障特征频率外，还包括轴承固有频率、随机脉冲和轴转动引起的谐波频率成分等[8]。此外，滚动体和内圈故障特征频率被保持架特征频率和转频调制，出现边频效应，造成滚动体和内圈故障特征提取困难。因此，轴承故障诊断的过程是一个对采集的信号进行降噪，滤除不感兴趣的频率成分，实现故障特征增强和故障特征提取，最终完成故障分类及故障程度定量评价的过程。

滚动轴承表面损伤故障类型包括外圈故障、内圈故障、滚动体故障、保持架故障及其复合故障。复合故障在实际工程中更为常见[9]。复合故障不是单故障的叠加，而是它们之间相互耦合的结果。发生复合故障时的轴承某些部件的特征频率幅值会明显增大[10]，且强故障特征往往会湮没弱故障特征，导致弱故障难以被识别。因此，轴承复合故障具有相互耦合及强度不平衡的特性，增加了从复合故障原始信号中分离并提取出单个故障特征的难度。

2 复合故障的传统诊断技术

滚动轴承工程应用中，基于振动信号的故障诊断方法是最为常用、可靠的方法[11]。目前广泛应用的传统滚动轴承复合故障诊断方法主要有经验模态分解及其衍生方法、小波变换、经验小波变换、盲源分离、共振解调和解卷积等。

2.1 经验模态分解及其衍生方法

2.1.1 经验模态分解

经验模态分解（empirical mode decomposition，EMD)能够根据信号内在特点自动地将信号分解成多个几乎相互正交的本征模态函数（intrinsic mode functions,IMF），已经广泛用于非线性、非平稳信号的特征分离[12]。崔玲丽等[13]借助EMD 的自适应分解特点，将信号分解为IMF 集合，再结合独立分量分析（ICA），实现了轴承复合故障特征分离。马新娜等[14]针对从单通道振动信号中进行复合故障特征分离提取困难的问题，采用EMD 对振动信号进行分解和重构，再利用自适应陷波器依次筛选出故障，从而有效地分离复合故障。韩嘉华等[15]采用EMD 对同源双通道信号进行分解与重构，然后通过全矢谱技术融合重构信号，最后对融合信号作频谱分析，成功提取出故障特征，有效解决了单通道下采集的轴承复合故障信号不完备问题。

EMD 也存在许多不足。EMD 的端点效应和噪声敏感性都会导致分解结果存在模态混叠现象，且EMD 算法没有严格的数学理论依据，有待于进一步的数学推导证明[16]。基于EMD 方法存在的缺陷，Wu 等[17]提出了EMD 的改进方法——总体经验模态分解(ensemble empirical mode decomposition,EEMD)算法。该方法利用白噪声均值为零的特性改善EMD 模态混叠现象，在原始信号上叠加不同高斯白噪声并进行多次EMD 分解操作，然后对多次分解产生的IMFs 进行平均处理。

Lei 等[18]对图1（a）中包含调制和冲击分量的仿真信号分别进行EEMD 和EMD 分解，结果如图1（c）、（d）所示，经过对比分析，发现EEMD 可以准确提取信号的模态特征分量，并有效抑制了模态混叠现象。此外，图1（b）所示EEMD 的分解误差远小于EMD 的分解误差，证明了EEMD 方法的分解效果优于EMD 方法。针对强背景噪声下轴承振动信号信噪比低的问题，颜天晓等[19]采用EEMD和希尔伯特(Hilbert)包络分析方法，有效地消除了噪声的干扰，实现了轴承复合故障特征分量的分离和特征提取。

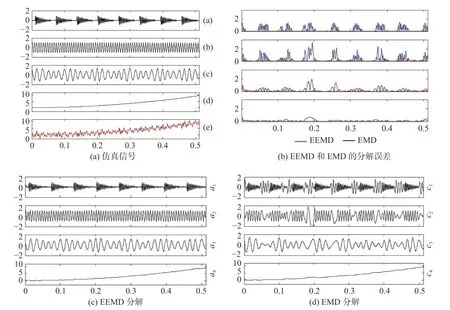
图1 EMD 和EEMD 分解效果图[18]Fig.1 EMD and EEMD decomposition results[18]

事实上，EEMD 并未完全消除EMD 的模态混叠现象，只是一定程度的改善。信号通过EEMD处理，可能会产生若干植入性IMF，在这种情况下，需要对多级IMF 做平均，这可能导致虚假分量的产生。此外，EEMD 需要人工经验来设置白噪声的数值，工作量大，若数值设置不当，也无法有效地减少模态混叠。

2.1.2 局部均值分解

在EMD 原理基础上，SMITH[20]提出了局部均值分解算法（local mean decomposition,LMD)。与EMD 不同的是，LMD 将原始信号分解为若干个乘积函数(product functions,PF)，而不是本征模态函数（IMF），每个PF 都由一个包络信号和一个特定尺度且具有真实物理意义的纯调频信号的乘积表示。LMD 可以降低原始信号中的噪声和其他干扰成分，得到更准确的真实信号。因此，LMD 可用于原始信号的降噪提纯。

王普等[21]为解决滚动轴承复合故障特征频率相近而分离困难的问题，首先对原始信号进行LMD 处理，滤除噪声干扰，然后结合多尺度熵能量进行故障特征提取。对比仅采用多尺度熵或能量的特征提取方法，该方法故障特征提取精度和诊断准确率有较大提升。与EMD 一样，LMD 也存在模态混叠，为改善这缺陷，程军圣等[22]借助噪声辅助方法，提出了总体局部均值分解(ensemble local mean decomposition,ELMD)算法。该算法首先向原始信号中添加能量有限的独立白噪声，然后利用LMD 思想将附加噪声的信号多次分解为若干乘积函数集合，并求多次分解结果的平均值得到最终分解结果。杨斌等[23]提出一种基于ELMD 与MCKD的轴承复合故障诊断算法。该方法先通过最优参数MCKD 提取轴承的主要故障，再利用ELMD 将信号故障特征频带分解到不同模态分量并剔除主故障，最后采用MCKD 识别其他故障，从而实现了复合故障的分离和提取。ELMD 本身也存在缺陷，若白噪声不能被完全中和，会影响分解效果，从而导致重构误差。针对此缺陷，柴慧理等[24]在ELMD 的基础上添加符号相反的白噪声以达中和目的，再与排列熵进行结合，将高频白噪声分量直接剔除，从而有效提取了滚动轴承复合故障特征。

2.1.3 变分模态分解

变分模态分解（variational mode decomposition，VMD）是一种适用于非平稳信号的非递归时频分析方法[25]。与EMD 相比，VMD 在抗模态混叠、计算及收敛速度和噪声鲁棒性上有着明显优势。VMD的自适应性表现在不仅能自适应地确定模态个数，还能对每个模态的最佳中心频率和带宽进行估计，将信号分解为带限的固有模态函数的集合，从而实现模态分量的有效分离。

在轴承复合故障诊断中，在强背景噪声干扰下容易导致误诊或者漏诊。万书亭等[26]针对复合故障信号相互干扰难以分离的问题，运用VMD 降噪，通过MCKD 实现轴承和齿轮故障分离，取得了良好诊断效果。Tang 等[27]为了克服由于传感器数量有限导致的测量信号无法充分表达多振源和传递路径信息的不足，采用VMD 方法将多路振动信号分别分解为若干有限带宽的模态分量，再将多路的模态分量信号进行希尔伯特变换，并结合独立成分分析（ICA），实现了轴承复合故障特征分离和提取。

VMD 改善了EMD 的端点效应和模态混叠问题，但其信号处理效果受惩罚参数 α和模态分量分解个数k的影响，这2 个参数值需要先验知识来确定，增加了其应用于工程的困难。针对该问题，Zhang等[28]将基尼指数和自相关函数加权结合，构造优化目标函数，采用粒子群算法（PSO）对 α和k寻优，从而实现滚动轴承复合故障诊断。Miao 等[29]结合峭度和包络谱峭度，构造了集合峭度指标，以此为优化目标并利用Grasshopper 算法寻优 α和k，实现了机车轴箱轴承故障特征提取。张青松等[30]提出了一种从能量熵变化率角度选择VMD 模态个数k的方法，同时使用改进的粒子群优化算法优化支持向量机，实现了对多种轮对轴承故障的有效识别。

2.2 小波变换

与短时傅里叶变换（STFT）的分辨率固定不同，基于小波的方法具有多尺度、多分辨率的能力，能够自适应地对非平稳信号进行多分辨率分解，故在轴承复合故障诊断领域得到了广泛应用。

2.2.1 连续小波变换

连续小波变换(continuous wavelet transform，CWT)与傅里叶变换(Fourier transform,FT)类似，也是利用某个基函数族来表示信号，不同之处在于，CWT 的基函数为小波函数族，而FT 的基函数是余弦和正弦函数族。CWT 将信号分解为小波基函数的线性组合，这些小波基函数由母小波函数ψ(t)缩放和平移产生[31]。小波基函数定义为

式中：ψτ,s(t) 是小波基函数；尺度s控制母小波的伸缩；平移量 τ控制母小波的时移。尺度s与频率反比对应，平移量 τ与时间对应。由于小波基函数包含2 个特征参数（尺度参数s和平移参数τ），因此，使用小波基函数变换信号意味着信号将被投影到二维时间尺度平面。CWT 定义为

式中ψ∗(·)表示ψ (·)的复共轭。

骆志高等[32]利用Gabor 小波变换进行单一故障特征提取，并采用模糊数学可能性理论完成了滚动轴承复合故障的诊断。Cheng 等[33]将振动信号的CWT 形成的时频图作为卷积神经网络的输入，从而实现了滚动轴承复合故障诊断。

CWT 中的平移量和尺度参数连续变化，计算量较大，不满足在线故障诊断的实时性要求。在CWT 的基础上，出现了适用于数字计算的离散化版本——离散小波变换。

2.2.2 离散小波变换

将CWT 中的尺度参数s和平移量 τ离散化，形成离散小波变换（discrete wavelet transform，DWT）。DWT 非常适合于离散采样数据的处理。离散小波变换计算效率高，故得到广泛应用[34]。信号x(t) 在尺度 2j和位置k2j的DWT 定义为

式中k,j为正整数。

莫代一等[31]基于并联双重Q因子的小波变换分析方法，实现数据降噪和升维，通过原始振动信号获得多组低共振分量，再结合FastICA 方法，通过盲源分离，实现了复合故障的特征分离和提取。明安波等[35]对DWT 分解后的子信号进行频谱自相关计算，以突出故障特征分量，分离出内外圈故障特征。Fan 等采用正交DWT 对振动信号进行分解，得到其在多个层次上的能量色散，并将能量色散作为故障特征，再利用广义似然比检验的统计学方法，有效提取和识别出轴承复合故障特征，该方法效果优于EMD 和希尔伯特包络谱分析算法。

DWT 可以实现信号多分辨率分析，低频段拥有高分辨率，但由于其忽略每一级分解中的高频段，且其频带是按二进制离散，因此在实际应用中存在不能准确提取所需频带信号分量的隐患。另外，由于参数离散化处理，DWT 缺乏平移不变性。

2.2.3 小波包变换

小波包变换（wavelet packet transform,WPT）是小波变换的改进。在小波变换中未分解的高频段的细节信息，WPT 能对其进行进一步分解，提高高频段分辨率，从而实现信号全频段的重构。

唐贵基等[36]使用改进谐波小波包分解对轴承复合故障信号进行处理，根据计算得到轴承故障特征频率确定分解层数，并自适应确定故障频带，最后通过带通滤波和能量算子包络解调，实现了轴承复合故障特征的分离和提取。马本栋等[37]使用多小波包变换进行信号重构，使用分量排列熵作为故障特征评判标准，选取故障特征丰富的子信号分量重构出单故障信号，最后通过能量算子解调，实现了轴承内外圈故障特征频率及其倍频的分离和提取。表1 为轴承部件理想故障特征频率，诊断结果如图2 所示，轴承外圈和内圈故障频率均被检出。Wan 等[38]提出了一种基于最大重叠离散小波包变换（MODWPT）和故障能量比（FER）的诊断算法。首先对采集的振动信号进行MODWPT 处理，得到一组频带信号，然后选择FER作为评价指标，计算每个频带信号的FER 值并生成FER 图，最后选择包含丰富故障信息的FER 值最大的频带信号进行包络谱分析，实现了复合故障诊断。

表1 滚动轴承故障特征频率[37]Tab.1 Fault characteristic frequency of rolling bearing[37] Hz

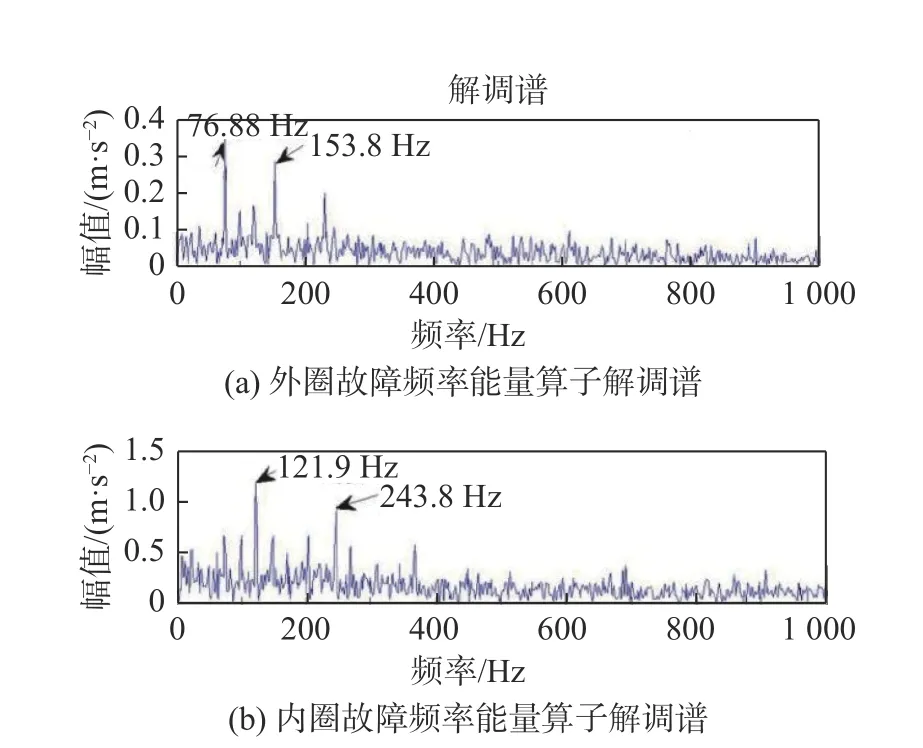
图2 多小波包重构信号能量算子解调谱图[37]Fig.2 Teager energy spectrum of reconstruction signal[37]

与DWT 相比，小波包变换实现了信号全频段重构，但是WPT 信号重构时，可能会因隔点采样出现频率混叠现象。

2.2.4 第二代小波和多小波

第二代小波变换（second generation wavelet transform,SGWT）利用提升策略取代了经典DWT 的变换策略，其实现过程包括分解、预测和更新3 个步骤：1）利用分解算子将原始信号序列分解为偶序列和奇序列；2）根据预测算子使用偶序列预测奇序列，将预测差值定义为细节信号；3）利用细节信号更新偶序列，继而得到近似信号[39]。SGWT 不依赖Fouerier 变换，且小波基也不是由母小波平移和缩放形成，其所有运算均在时域完成，不仅能将信号分解于不同频带，还可凭借预测系数和提升系数的优化设计获得具有独特功能的小波基函数，使得为不同故障特征构造相应小波基函数成为可能[40]。

基于小波的故障诊断通过匹配和提取与给定小波函数最相似的故障特征来实现，但是故障类型不同通常会导致故障脉冲波形不一致，甚至同类型故障由于监测点位不同或传递路径不同也会使最终的故障脉冲波形产生差异。为克服只使用一个小波函数来捕捉故障特征的局限性，在SGWT 的基础上可引入多小波函数来匹配一个或多个故障特征[41]。Chen 等[42]以包络熵最小为优化目标，将改进的自适应冗余提升多小波变换，利用多小波的多个基函数匹配多故障特征，实现滚动轴承复合故障诊断。其仿真和试验结果验证了改进方法诊断效果优于希尔伯特-黄变换（HHT）、维格纳-维尔分布（WVD）和CWT，其复合故障特征提取效果如图3 所示，外圈故障特征频率为43.8 Hz 和内圈故障特征频率为58.2 Hz均被有效识别。廖强等[43]为了使多小波能够自动匹配多故障，提出了一种预测算子和更新算子的自动优化策略。该方法可以根据观测信号的特性自动匹配小波基，实现复合故障的分离提取，台架试验证明了该方法是有效的。

图3 复合故障特征提取包络谱图[42]Fig.3 Envelope spectrum of compound fault feature[42]

SGWT 方法中最重要的步骤是构建预测和更新算子。如果缺少向量预测的个数，分解结果会出现频率混叠现象。设计性能优良的矢量预测和更新算子对提升SGWT 的性能具有重要意义。

2.2.5 双树复小波变换

Wang 等[44]提出了采用双树复小波变换（dualtree complex wavelet transform,DTCWT）的复合故障诊断方法。与DWT 和SGWT 相比，DTCWT 具有更好的平移不变性并能减少频率混叠，非常适用于提取轴承故障中周期性冲击特征，并通过试验验证了其故障特征提取效果优于SGWT 和快速谱峭度方法。胥永刚等[45]采用DTCWT 对采集到的轴承振动信号进行故障特征增强和降噪处理，再通过独立成分分析（ICA）对降噪后的混合信号进行盲源分离，以抑制频率混叠现象，最后通过包络谱实现复合故障特征的分离与故障识别。

DTCWT 的平移不敏感性的优点源于实部小波基和虚部小波基间的希尔伯特对关系[44]。DTCWT改善了时移缺陷和频率混叠，但不能从根本上消除频率混叠，因此，DTCWT 尚需要继续改进。

双树复小波包变换（DTCWPT）对DTCWT 算法中未进行细分的高频部分进行分解，降低了信息丢失。文献[46-47]采用DTCWPT 结合自回归（AR）谱和ICA 对滚动轴承复合故障完成了特征分离和故障诊断。文献[48-49]将DTCWPT 作为振动信号预处理方法，每个频带构造一个原始特征集，作为机器学习算法的输入，通过人工智能完成轴承复合故障诊断。

2.3 经验小波变换

Gilles[50]结合EMD 自适应模态分解和小波多分辨率时频解析的特性，提出了经验小波变换（empirical wavelet transform,EWT）算法。EWT 算法兼顾EMD 的自适应性和小波分析的优点，首先根据频谱极值将其划分为多个连续区间，然后在每个频域区间上自适应构造正交小波带通滤波器组并提取信号中的调幅调频成分，最后通过希尔伯特变换获得有物理意义的瞬时频率和幅值，实现特征分离和提取[51]。Cao 等[52]将EWT 用于铁路货运列车和普通列车轴箱轴承的复合故障检测，对EWT分解出的信号分量施加包络解调操作，基本实现了外圈与滚动体复合故障特征的提取，但是故障特征不够明显，故障特征频率的谐波成分被强噪声所湮没。Chen 等[53]提出了数据驱动阈值的小波空间邻域系数去噪和EWT 相结合的故障诊断方法，克服了强背景噪声对EWT 模式识别的影响，成功应用于风力发电机轴承复合故障特征识别。

针对EWT 依据局部极大值进行频谱分割存在的不确定性问题，Wang 等[54]提出了一种稀疏引导的EWT 算法。该算法利用稀疏函数指导EWT 自动分割傅里叶频谱区间，实现了列车轴承外圈和滚子复合故障识别。随后，Wang 等[55]又提出了一种EWT 分割片段优化方法，将传统EWT 中根据频谱极大值进行频段分割问题转化为一个约束优化问题，首先对数据进行预白化处理，去除一部分低频分量，接着以最大化平方包络谱峭度为收敛条件进行频带分割，并分别使用一个带通滤波器、一个高通滤波器和一个低通滤波器重构信号，最后对重构信号施加平方包络谱操作完成多故障特征提取。试验结果表明，该方法可以识别轴承滚子和外圈复合故障。针对EWT 的边界确定难题，刘士铭等[56]给出了一种自适应边界选择方案，以使不同频带内信号的峭度最大化为目标选取频谱分割的边界，使用频谱内信号峭度的局部极大值进行边界频带划分，频域峭度曲线如图4（a）所示，频带边界如图4（b）所示，然后进行EWT，实现了滚动轴承复合故障的分离与识别。

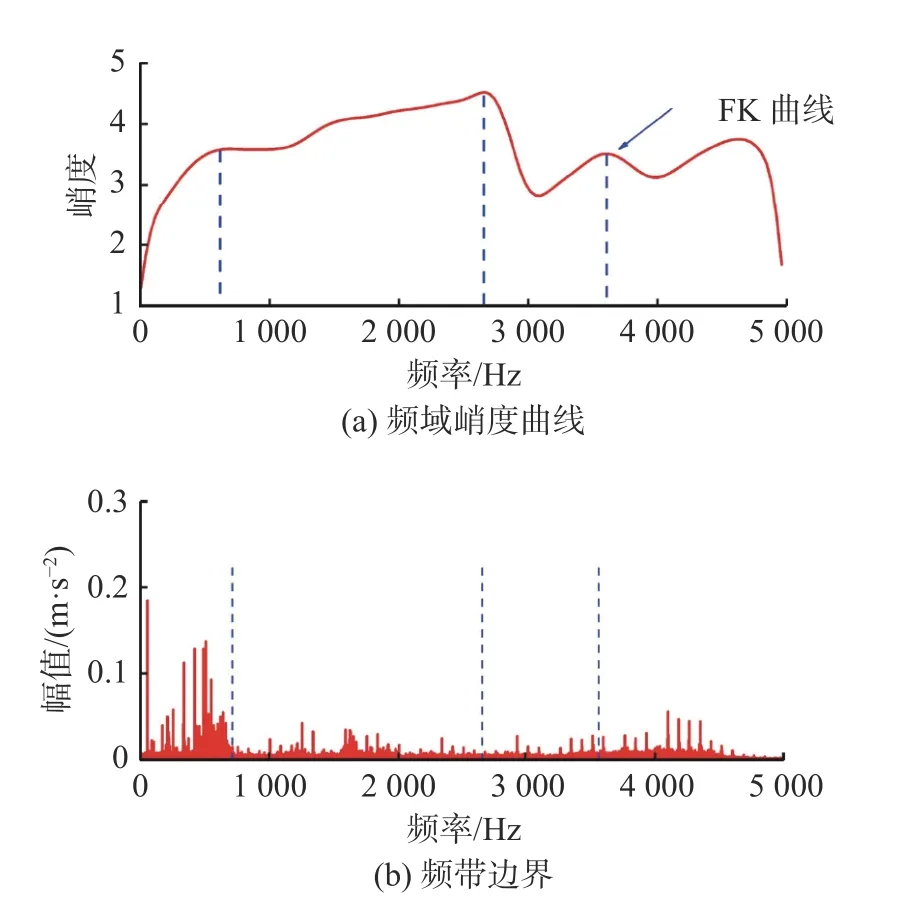
图4 基于谱峭度曲线的自适应边界分割EWT 方法[56]Fig.4 Adaptive boundary partitioning method based on SK curve of EWT[56]

EWT 算法的关键在于傅里叶频谱的区段划分，当振动信号处于强噪声背景下或者随机冲击分量较多时，如何自适应地分割频谱，提取感兴趣的频带，仍然需要深入研究。

2.4 盲源分离

盲源分离（blind source separation,BSS）指在源信号和传输信道参数缺失时，采取统计方法从观测到的混合信号中近似分离还原出源信号的技术，其目的是通过确定分离过程所需的参数，根据观测信号对源信号进行估计。BSS 在信号恢复方面具有显著优势[57]。其工作原理用方程式（4）描述，为

式中：X(t)=[x1(t),x2(t),···,xM(t)]是观测信号；S(t)=[s1(t),s2(t),···,sN(t)]是源信号；A是混合矩阵；n(t)是噪声信号。在S和A都未知的情况下，确定分离矩阵W，得到源信号S的最佳估计y，为

根据观测信号与源信号的数量关系，BSS 模型可分为超定、正定、欠定3 种类型。BSS 算法的经典算法有独立分量分析（independent component analysis，ICA)、非负矩阵分解（non-negative matrix factorization,NMF）和稀疏分量分析（sparse component analysis,SCA）。

2.4.1 独立分量分析

ICA 算法除需要源信号具有统计独立特性外，不需要混合信号的其他先验知识，是解决盲源分离问题的有效手段。该方法要求传感器数量大于或者等于源信号数量。由于机械系统的特殊性，传感器在布置位置和数量上常常受到限制，因此，在工程实际中，故障特征提取基本上属于欠定盲源分离范畴。此时惯用的解决方案是通过信号分解方法，将采集信号分解成若干个通道的子信号，再利用ICA 复原原始信号的故障信息，实现盲源分离。

Wang 等[58]首先采用EEMD 对轴承复合故障信号进行分解生成多通道信号，然后利用ICA 对每个通道信号进行滤波。该方法令特征识别更清晰。Tang 等[27]为了克服通过有限传感器采集到的信号不足的缺点，采用了VMD 和ICA 方法相结合的轴承复合故障诊断方法。为了解决变速工况下传感器数量有限的问题，Tang 等[59]采用VMD 理论构造虚拟角域多通道信号，再结合ICA，实现滚动轴承的复合故障检测。

2.4.2 非负矩阵分解

非负矩阵分解(nonnegative matrix factorization，NMF)算法把目标矩阵当作2 个非负矩阵相乘，由于“非负”特性，NMF 分解结果在某种程度更具备实际物理意义[60]。处理盲源分离时，NMF 需要较少的约束，收敛速度快，分解效率高。然而，在旋转机械的实际工作条件下，采集到的轴承振动信号较为复杂且信噪比低，用传统的NMF 算法特征提取效果并不佳。为提高盲源分离效果，NMF 必须对源信号和混合矩阵附加稀疏性、非平滑性等条件[57]。

朱晓洁[61]将稀疏性非负矩阵分解（SNMF）算法用于双谱时频图分解，再结合支持向量数据描述算法，实现了滚动轴承复合故障的智能诊断。针对NMF 算法约束性较差，对复合故障检测效果不佳的问题，王梦阳等[62]结合能量变分模态分解算法与局部非负矩阵分解算法，提取出振动信号所蕴含的复合故障特征。

2.4.3 其他盲源分离方法

除了上述2 种方法外，还有许多新型BSS 算法被应用到滚动轴承复合故障诊断领域。Hao等[63]提出了一种基于三维几何特征的稀疏分量分析(TGF-SCA)方法，利用源信号稀疏性，克服了ICA 非欠定性，且不要求源信号之间相互统计独立，在未知信号源数量的场景下，检测出了滚动轴承的复合故障。张江亚等[64]结合粒子群算法和BSS 算法，实现了多源复合故障特征分离。

现有的盲源分离算法在实际的应用中还存在一些不足亟待解决。例如：实际中，源信号并非都具有统计独立性，并且很多场合下源信号个数未知或信号个数动态变化；缺少在混合矩阵奇异情况下实现盲源分离的有效算法。

2.5 共振解调

滚动轴承表面缺陷会引发工件与故障表面的周期性冲击，这种冲击会激起轴承及其邻近部件的共振，并出现调制现象[65]。在多个故障共存的情况下，不同的故障脉冲极有可能激发出不同的谐振频率[66]。通过解调这些缺陷引起的共振，可以检测出不同轴承的故障或者单轴承的不同类型故障。

谱峭度（spectral kurtosis，SK）被定义为能量归一化的4 阶谱累计量指标。SK 具有对瞬态冲击信号敏感的特性，在被用于提取轴承瞬态冲击成分的应用中表现良好。Antoni 等[67]给出了SK 的正式定义，还指出SK 可用于识别信号中的非高斯成分及判断其在频域中的位置，并用于旋转机械故障脉冲信号频域位置的判断。基于SK，Antoni[68]提出一种基于STFT 的SK 估计方法，即Kurtogram 算法。在此基础上，Antoni[69]又提出了一种基于1/3 二进制滤波器组的快速谱峭度（fast spectral kurtosis，FSK）估计方法。此后，基于共振解调的轴承复合故障诊断方法便在SK 和FSK 的基础上快速发展起来。

Wang 等[66]提出了一种自适应SK 方法，将峭度作为适应度函数，通过迭代选取多个共振频带，实现滚动轴承复合故障特征提取。FSK 方法只能提取最大峭度值的共振频带，可能会使弱故障被淹没，且易受到强背景噪声影响的缺陷。Wan 等[70]将VMD 作为前处理方法，使含有不同故障特征信息的共振频带被分解到不同的IMF 中，然后通过FSK 提取出轴承单个故障，仿真和试验验证了该方法是有效的。

胡爱军等[71]以相关峭度最大值确定共振频带的中心频率。首先依据轴承结构参数计算内圈和外圈故障特征频率，根据采样频率分别计算解卷积周期，得到如图5（a）所示的相关峭度曲线，曲线最大值分别为1 512Hz 和3 812Hz，然后分别以它们为中心频率确定共振频带，最后通过共振解调得到了如图5（b）、（c）所示的故障特征图，实现了轴承内外圈复合故障的分离和识别。然而，该方法依赖于故障解卷积周期的选取，当轴承处于非稳态时，其故障脉冲周期可能发生变化，使其失效。文献[72]将SK 与最大相关峭度解卷积（MCKD）结合，将共振解调不能分离识别的故障进一步通过MCKD 处理，实现了复合故障的分离与识别。向玲等[73]使用SK 进行共振频带参数选取，将带通滤波后的信号进行多点最优调整，采用最小熵解卷积（MOMEDA）进行故障特征增强，实现了复合故障特征提取。沈健等[74]针对峭度指标对于单个随机冲击，即低密度冲击十分敏感，将快速谱峭度图用于高密度冲击故障频带时容易失效的问题，提出将轴承滚动体故障视作低密度冲击故障，外圈则为高密度冲击故障，分别利用快速谱峭度图和变带宽包络谱峭度图，提取出滚动体和外圈故障共振频带。

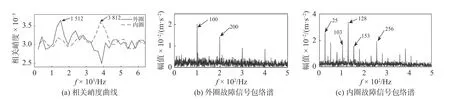
图5 基于相关峭度的共振解调方法[71]Fig.5 Resonance demodulation method based on correlation kurtosis[71]

为克服随机脉冲对SK 共振解调方法的影响，Chen 等[75]结合改进的冗余第二代小波包变换（RSGWPT）和平方包络谱稀疏准则，提出了一种自适应共振频带解调方法。RSGWPT 的改进方法可以很好地将复合故障信号分解成独立的子带，实现故障相关特征的精细分离，然后结合峰值搜索算法，利用所建立的包络谱稀疏图识别出复合故障激发的所有最优共振频带，最后通过带通滤波和包络解调实现对复合故障的准确识别。Zhang 等[76]提出了谐波谱峭度（harmonic spectral kurtosis，HSK）指标，该指标具有抗噪声能力强和抗单脉冲干扰能力强的优点。HSK 可以提取包络谱中的谐波信息，量化信号中的周期脉冲。根据HSK 指标，文献[76]提出了Harmogram 频谱分割方法。该方法可以提取预先设定的特征频率范围及其谐波组成新的样本，去除噪声而保留故障信息，从而达到故障特征增强的效果。该方法首先利用频谱的傅里叶变换函数反提取趋势分量，用于将频谱划分为几个频带，通过尺度函数和经验小波，对每个频带的中心频率和频带宽度进行处理，得到一组带通滤波器和一个低通滤波器，使用每个滤波器提取一个分量，然后增加拦截长度，重复上述步骤，形成多层次塔形边界分布图，最后计算各经验模态包络谱的谐波谱峭度，得到Harmogram 来识别信号中的周期脉冲信息。图6 示出使用Harmogram 方法进行轴承内外圈复合故障诊断的过程。图6（a）、（d）分别为基于外圈和内圈故障特征频率计算的Harmogram；图6（b）、（e）分别为基于外圈和内圈故障特征频率得到的HSK 最大分量的波形和频谱，图6（c）、（f）分别为外圈故障和内圈故障滤波信号的包络谱。可以看出，故障特征基频及其倍频都十分明显。该方法在提取周期性脉冲信息的效果优于其他谱峭度分析方法。

图6 Harmogram 方法对轴承内外圈复合故障的诊断过程图[76]Fig.6 Harmogram for the diagnosis process of compound fault of inner and outer rings of bearings[76]

当轴承发生复合故障时，不同故障所激起的共振频带可能互不干扰或有重叠，加大了从共振频带中提取单故障的难度，因此，如何正确选取带通滤波参数（频带中心和带宽）是共振解调分析的关键。SK 对大的随机脉冲非常敏感，但这些脉冲不一定是轴承故障引起的脉冲，且存在噪声干扰，相对较弱的故障分量可能会被能量更强的故障分量或噪声分量淹没，导致通过SK 确定共振带时失效，从而出现误诊或漏诊。目前基于SK 的共振解调方法的研究主要集中在频带分割方法（STFT/FIR）和计算指标（峭度）的改进[70]。未来的共振解调方法应朝着自适应分割共振频带的方向发展，并与其他信号处理方法结合使用，使其在强噪声环境和变转速等复杂工况下具有更好的鲁棒性。

2.6 解卷积

基于峭度指标的一类重要的信号处理方法是共振解调，其主要思想是根据峭度指标在频域确定共振频带，为带通滤波参数提供参考。另一类方法是解卷积。在某种意义上，振动信号可被假设为故障引发的周期性冲击信号与机械部件共振响应卷积的结果，因此，解卷积经常被用来还原故障周期性冲击信号[77]。

2.6.1 最小熵解卷积

最小熵解卷积（minimum entropy deconvolution，MED)通过构造长度和系数恰当的 FIR 逆滤波器，并以峭度值最大为滤波器系数更新准则，使得经过逆滤波器滤波后的输出信号能够逼近原始脉冲信号，可用公式(6)表达。

式中：y(n)为传感器收集到的振动信号；x(n)为轴承故障脉冲信号；h(n)为系统频率响应函数；*表示卷积；e(n)为背景噪声。

He 等[78]首次将MED 用于轴承复合故障诊断，将MED 与SK 结合，解决了MED 单独作用时多故障中的一些共振频带被抑制的问题，首先利用峭度谱图寻找出原始振动信号中的敏感共振频带，接着通过带通滤波抽取单个故障信号，最后通过MED 和包络分析识别出所有单个轴承故障。陈海周等[79]针对强背景噪声影响下的轴承复合故障诊断问题，提出了将MED 与Teager 能量算子结合的方法。MED 用于前处理，增强信号故障脉冲特征，提高信噪比；Teager 算子增强冲击特征：因此，先MED 滤波，再经过Teager 能量算子处理，信号的瞬时变化和冲击成分更加突出，最后通过Teager能量谱即能够实现复合故障特征提取。

MED 方法的局限性在于解卷积是针对单个脉冲或者一组脉冲进行的。文献[78]证明了MED无法检测到卷积过程中被抑制的共振频带中的故障冲击成分，这意味着MED 有时无法单独处理并分离轴承复合故障特征信号，因此，MED 经常被用作轴承复合故障诊断的前处理或后处理方法。

2.6.2 最大相关峭度解卷积

最大相关峭度解卷积（maximum correlation kurtosis deconvolution,MCKD）由MED 发展而来，是对周期性脉冲进行增强的有效手段。MCKD 通过引入周期先验指标——相关峭度，大幅提升算法对感兴趣周期性脉冲信号的敏感程度。通过迭代优化滤波器系数，使得滤波后的信号相关峭度值达到最大，MCKD 即可实现相应周期性脉冲信号的增强与提取[80]。

钟先友等[81]将MCKD 作为重分配小波尺度谱的前处理方法，通过设定不同的解卷积周期，对原始信号进行降噪和单个故障特征分离，实现了轴承内外圈故障特征的分离和提取。王志坚等[82]提出了基于MCKD 与循环自相关函数解调的复合故障特征提取算法，成功提取了轴承复合故障特征。

针对MCKD 需要人工选取解调参数的不足，朱丹宸等[83]提出了一种改进的MCKD 方法，对采集的原始振动信号，根据不同故障设定不同的初始周期T，采用粒子群算法选取最优滤波器长度L和移位数M，最后将滤波后所得信号的包络谱与Teager 能量谱进行互相关计算，由互相关谱实现滚动轴承故障特征的提取与识别。图7（a）、（b）分别为得到的轴承内圈最优解卷积信号包络谱和Teager 能量谱；图7（c）为Teager 能量算子和包络的互相关谱；图7（d）、（e）和（f）分别为轴承外圈故障的诊断过程。可见，使用该方法可使轴承故障频率特征明显增强。朱江艳等[84]将FastICA 和参数优化MCKD 相结合，首先基于FastICA 实现复合故障双通道混合信号的盲源分离，然后使用相关峭度和平方包络熵构成的适应度函数进行滤波器长度L、移位数M和解卷积周期T的选取，最后通过希尔伯特包络解调完成复合故障的特征分离和提取。

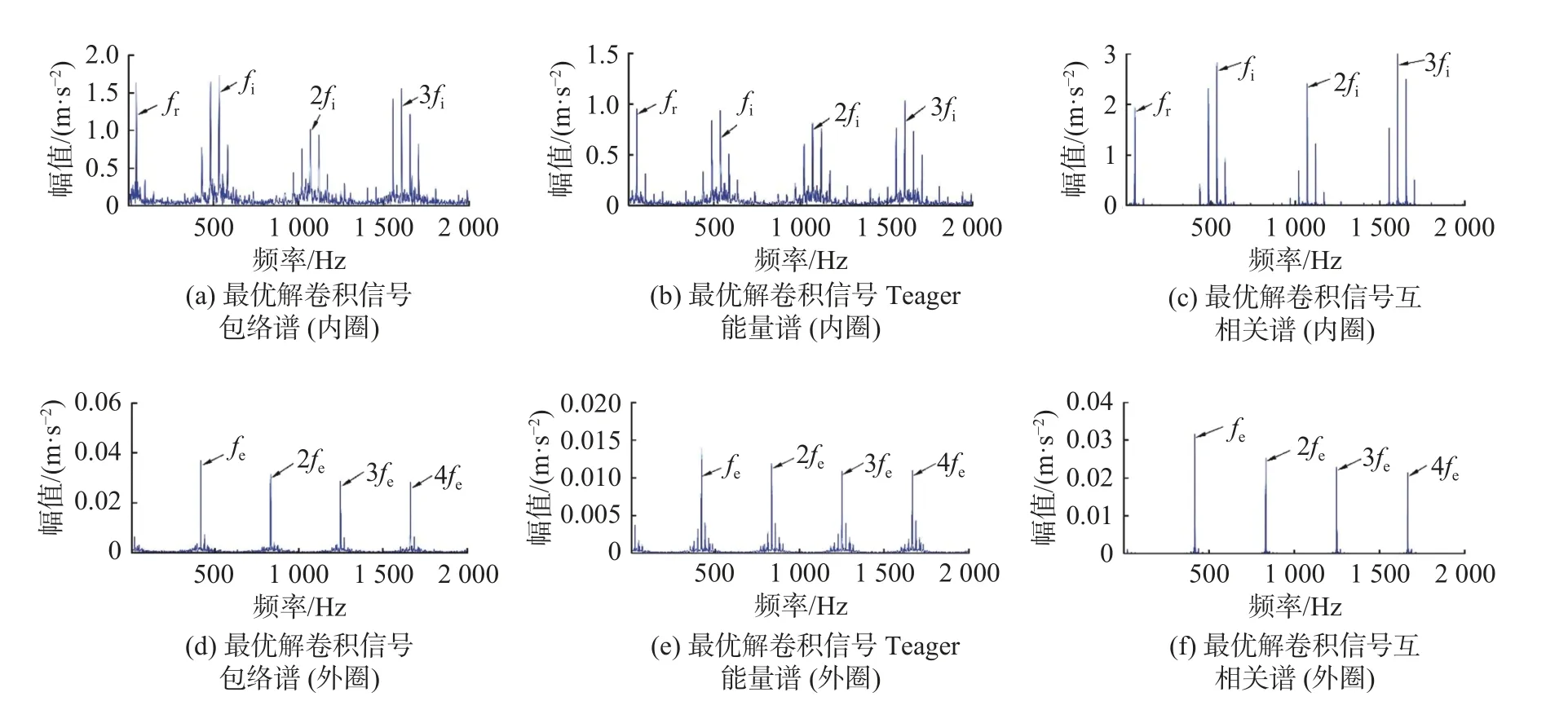
图7 基于互相关谱的滚动轴承复合故障诊断结果图[83]Fig.7 The result of rolling bearing compound fault diagnosis based on cross-correlation spectrum[83]

MCKD 方法的核心是参数T、L、M的选取。参数T的选取需要一定的先验知识，在考虑参数之间关联的前提下，快速、自适应地选取最优参数，是提升MCKD 诊断效果的关键。故障特征周期为非整数时，需要对采集的振动信号进行重采样，以求得整数形式的解卷积周期T，这种严格的要求和复杂的过程常使诊断效果变差。此外，MCKD 属于迭代算法，其迭代次数会影响最终结果。综上，MCKD 是一种适合提取周期性冲击的信号处理方法，参数的最优化选取是算法性能优劣的关键。

2.6.3 多点最优调整的最小熵解卷积

针对MCKD 需要预先确定故障冲击信号的周期，计算代价高的缺点，多点最优调整的最小熵解卷积（multipoint optimal minimum entropy deconvolution adjusted,MOMEDA)算法被提出。MOMEDA通过寻找一个最优滤波器，抵消传输路径的影响，提取脉冲信号的特征。它利用时间目标矢量来定义解卷积，从而确定脉冲的位置。该算法无需迭代即可获得最优滤波器，且不需要预先确定故障周期，更具一般性[85]。

齐咏生等[86]将自适应信号稀疏共振分解（ARSSD）作为MOMEDA 算法的前置处理方法，实现了对轴承内圈、外圈和滚动体复合故障诊断。该方法使用布谷鸟算法优化ARSSD 获得包含轴承故障脉冲的低共振分量，通过计算其多点峭度谱确定MOMEDA 最佳滤波器长度和故障周期，然后通过不同输入故障周期的MOMEDA 将复合故障分离并提取出来，最后通过包络谱分析完成故障特征提取和识别。Fan 等[87]采用ARSSD 和多点稀疏-多点最优最小熵解卷积（MS-MOMEDA），提取出不同干扰源下的轴承复合故障特征。该方法首先采用ARSSD 处理原始振动信号，得到低共振分量，然后根据多点峭度谱确定可能的冲击信号个数及其故障特征周期，从而实现了基于MOMEDA完成不同类型故障信号的针对性提取。图8 为基于MS-MOMEDA 和ARSSD 的方法对滚动轴承内外圈和滚动体复合故障的诊断示意图。多点峭度谱图确定的轴承故障特征周期分别为65.3、105.68和162.8，然后设定周期范围分别为[60,70]、[100,110]和[157,167]进行MOMEDA，最后通过包络解调得到内圈、外圈和滚动体故障特征频率及其倍频。

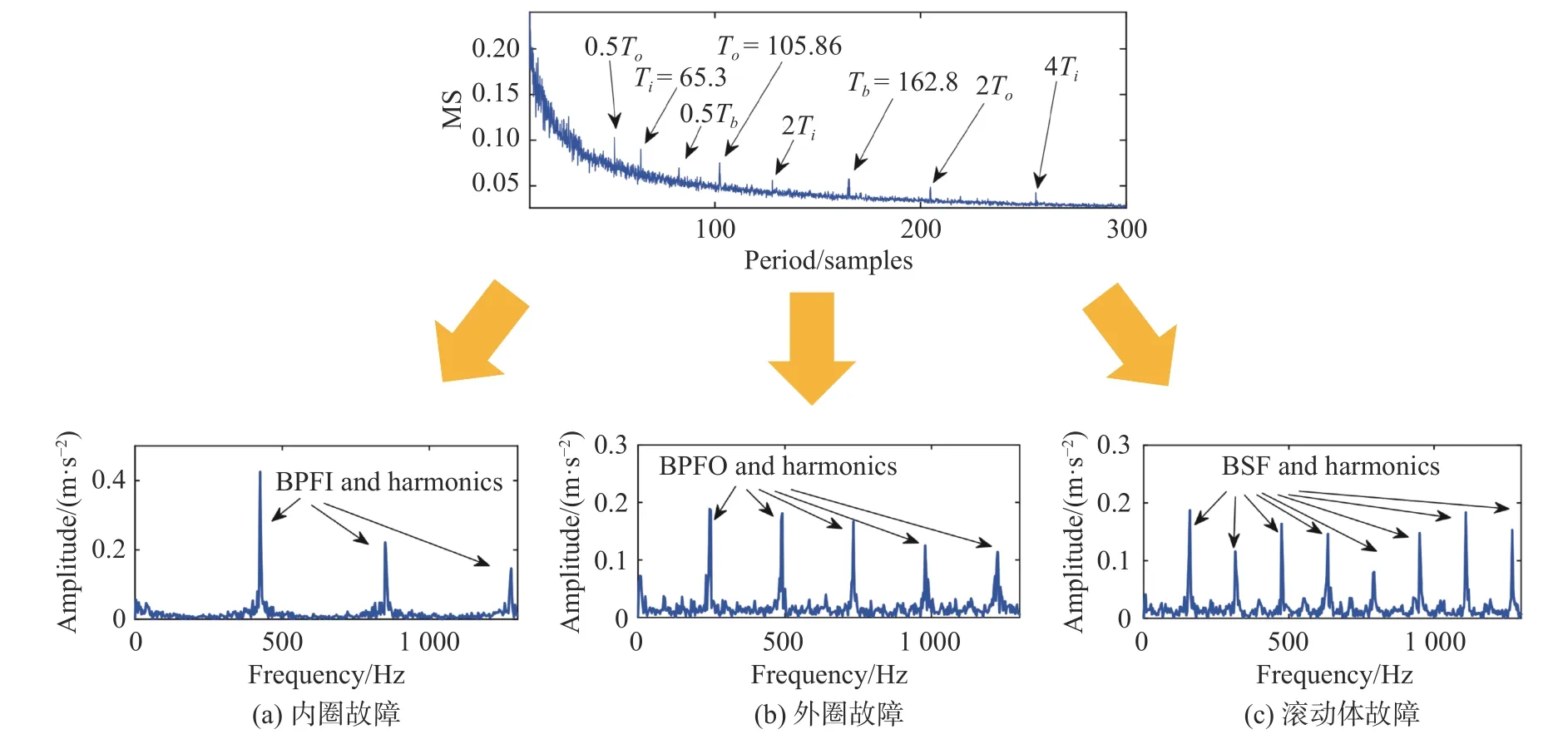
图8 轴承复合故障诊断示意图[87]Fig.8 Compound fault diagnosis diagram of rolling bearing[87]

MOMEDA 方法中解卷积周期的选取依赖先验知识，如何自适应完成解卷积周期的选取是未来算法改进的重要研究方向。与MED 相比，MOMEDA 克服了对单个随机脉冲敏感的缺陷。与MCKD相比，MOMEDA 计算效率更高且输入解卷积周期可以为非整数，并且不需要增加误差的重采样过程。但它仍然存在不足：1）仍然对周期先验的准确性有较高要求，这极大地决定了它性能的好坏；2）在强噪声干扰下，搜索的周期性脉冲可能是虚假分量；3）降噪的精度受搜索间隔和滤波器长度大小的影响[85]。因此，为尽可能地降低降噪间隔，需要对故障周期进行评估和优选，从而提高识别精度。

2.7 其他传统复合故障诊断技术

除了上述方法，还有很多优秀的轴承复合故障检测算法被陆续提出。

阶比分析方法是目前常见被应用于变速条件下旋转机械的故障诊断方法。它的主要思想是基于非平稳原始时域信号进行等角度的重采样构造角域伪平稳信号，以此消除变转速带来的影响[88]。沈仁发等[89]利用计算阶次追踪（COT）进行瞬时信号重采样，然后结合小波包和粗糙集，得到了滚动轴承的故障诊断决策规则，并通过轴承复合故障试验进行了验证。王晓龙等[90]将COT、MCKD 和自互补顶帽（STH）算法结合，实现了变速工况下轴承复合故障诊断。该方法首先使用COT 获得伪平稳的角域信号，接着通过果蝇优化算法对MCKD和STH 进行参数优化，然后经MCKD 滤波分离单一故障特征分量，最后结合STH 解调和包络分析来判断轴承健康状态。

稀疏表示是一种在强噪声背景下提取故障信息的有效方式。稀疏表示的原理是通过线性组合给定字典中的原子来表示原始信号。所用的原子越少，信号表达方式越精练，就越容易获得信号中隐藏的本质信息。针对滚动轴承多故障特征相互干扰、相互耦合的问题，郑胜等[91]通过级联过完备字典的稀疏表示实现了轴承内外圈复合故障。该方法首先通过分析信号频谱找到共振频带，然后对共振频带的信号分量构建级联过完备字典，计算出稀疏系数并分别进行单个故障信号重构，最后通过希尔伯特包络谱实现故障诊断。Deng 等[92]针对正交匹配追踪（OMP）在稀疏表示中求解困难的问题，利用人工蜂群（ABC）算法全局寻优性能强和收敛速度快的特点，获得近似最佳原子，再结合人工鱼群（AFS）优化的MCKD，更有效地诊断出滚动轴承的复合故障。

奇异值分解（singular value decomposition,SVD）作为降维和去噪的有效工具，能够反映奇异分量的能量特征。目前，SVD 已被广泛应用于信号处理和故障诊断领域。多分辨SVD 是SVD 的一种衍生算法。该方法引入矩阵二分递推构造原理，在保留SVD 抑制噪声优点的同时，还具备对微弱特征提取的能力。孟智慧等[93]借鉴了小波变换的思想，提出了多分辨率SVD 的方法，并将其用于轴承复合故障诊断。该方法首先使用多分辨率SVD 分解和重构原始信号，然后结合FastICA 算法，获得轴承单一故障信号，最后通过包络谱实现故障诊断。Zhou 等[94]结合多分辨率和有效奇异值分解理论，先利用多分辨SVD 的方法，得到逼近信号和细节信号，提高信号的维数，再采用有效SVD 方法对每个分量信号进行降噪和特征提取，最后结合ICA，实现了轴承复合故障诊断。

3 复合故障的智能诊断技术

基于数据驱动和人工智能的滚动轴承复合故障诊断方法具有人工参与度小、鲁棒性强和自降噪的特点，得到广泛应用。一般来说，传感器收集到的振动数据具有高维度、数量庞大和数据质量低的特点[95]，作为智能诊断算法的输入特征时，需要对数据进行分割、插值、降维等预处理，因此，智能诊断方法不能完全避免人工参与。目前使用较多的智能诊断算法包括基于人工神经网络（ANN）、极限学习机（ELM）和支持向量机（SVM）等传统机器学习算法，以及在此基础上发展出的深度学习算法和迁移学习算法等。机器学习主要用作模式识别，深度学习和迁移学习避免了繁琐的人工特征提取的过程，属于端到端的智能诊断算法。

3.1 机器学习

机器学习（machine learning,ML）是基于统计学理论发展而来的。基于机器学习的轴承复合故障诊断过程通常包括数据收集、特征选择、数据标签设置、信息分类或回归预测模型训练等步骤。首先采集原始振动数据进行白化、去均值等预处理，按照某些方式进行样本分割和样本特征的提取与选择，并将其组合成特征向量的形式，然后将标签制作好后进行训练样本集和测试样本集的划分，将训练集输入模型训练，最后使用测试集进行模型验证，评估其用于实际工程的有效性。

Lei 等[18]提出了基于EEMD 和小波神经网络（WNN）的滚动轴承复合故障诊断方法。该方法首先利用峭度指标选出EEMD 分解的敏感IMF，然后从选定的敏感IMF 的频谱和希尔伯特包络谱中提取10 个时域和频域特征，组装标签构成特征向量，最后将特征向量输入WNN 训练得到故障诊断模型，实现轴承的复合故障诊断。赵洪杰等[96]将非线性流形学习用于滚动轴承复合故障的识别。该方法选择经非线性流形学习进行维数约简过的时域信号协方差矩阵特征值作为原始特征集，然后通过K-means 算法实现轴承故障识别。余震[97]提出了一种基于近邻元分析法（NCA）的轴承复合故障诊断方法。模型分类器为NCA，输入为轴承故障振动信号中提取的多个时域特征组成的特征向量，通过训练集进行模型参数学习，最后将模型用于测试集，结果表明多维输入特征和NCA 的组合能够实现轴承复合故障诊断的任务。王普等[21]将LMD 作为原始信号的前处理，利用相关系数准则进行敏感PF 分量选取，然后计算其多尺度熵和能量，构建多尺度熵-能量(MSEE)特征向量，最后基于最小二乘SVM 实现了轴承复合故障诊断。

由于传统的ML 属于浅层学习，只能通过已有的训练样本优化诊断模型，因此，其诊断结果往往不理想，模型泛化能力较差。由于其输入特征向量集的特征有限，表征能力不足，十分依赖专家知识，因此，其鲁棒性较差。

3.2 深度学习

目前深度学习（deep learning,DL）是基于数据驱动的轴承故障诊断方法的热点研究方向[98]。DL 不需要精心设计的特征来对数据进行分类，降低了故障诊断中特征提取的难度和成本，并且比传统的浅层学习模型层数更多，其在特征提取和故障分类方面的能力也更为强大。

施杰等[99]提出了基于改进的希尔伯特-黄变换（HHT）与卷积神经网络（CNN）的轴承复合故障诊断方法。该方法采用多种群差分进化改进的EEMD 分解原始振动信号，基于距离测度最小原则筛选敏感IMF，通过改进的HHT 将敏感IMF 转化为时频图，并将其作为CNN 的输入，训练轴承复合故障诊断模型。该方法优于传统的BP 神经网络、STFT+CNN 和DWT+CNN 方法。姚德臣等[100]将CNN 用于城轨列车的轴承复合故障诊断，并通过试验验证了这一方法的可行性。该方法的模型输入为原始振动信号通过标准化及升维操作转化而成的二维灰度图。刘磊等[101]提出了一种可以实现自动特征提取的轴承故障诊断方法。该方法以原始振动数据时域序列为输入，利用Inception V3 模块和双向长短时记忆网络实现故障特征提取和故障诊断。图9（a）为诊断模型结构示意图；图9（b）为故障识别结果的多分类混淆矩阵，其中红框为复合故障；图9（c）为分类效果可视化图。

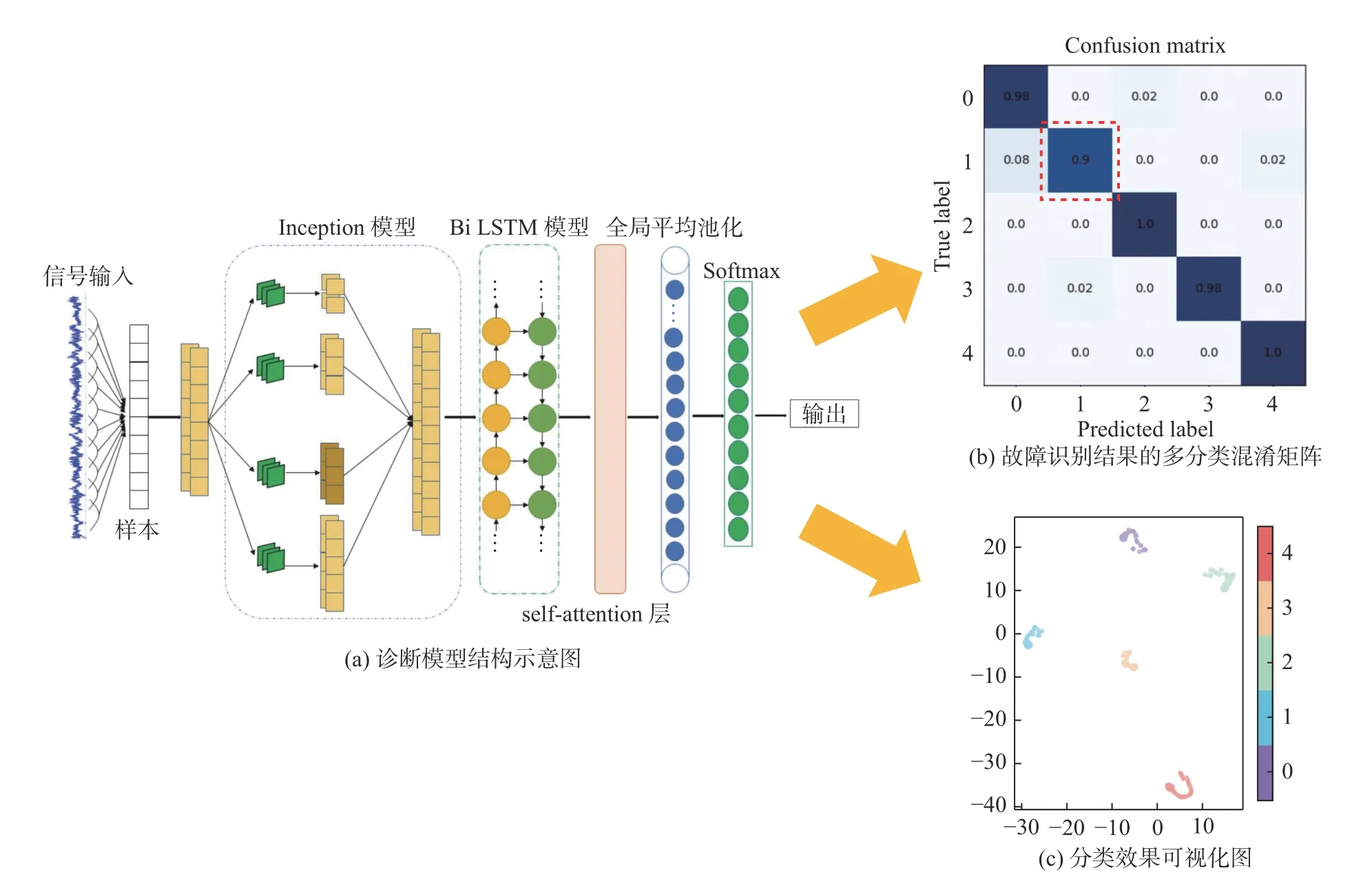
图9 基于Inception V3-BiLSTM 模型的滚动轴承故障诊断模型及效果图[101]Fig.9 Rolling bearing fault diagnosis model based on Inception V3-BiLSTM model and its effect diagram[101]

DL 算法的诊断效果取决于输入数据样本的质量和数量。为了实现准确的故障诊断，一般都需要大量数据样本。然而，在实际应用中，受数据样本的限制，训练深层模型来实现机器状态的精确故障诊断相对困难[102]。并且，在工程实际中的源域数据和目标域数据常属于不同分布，在这种情况下，基于传统DL 的诊断算法的性能会严重退化。

3.3 迁移学习

虽然基于深度学习的智能诊断技术在有监督的训练数据下取得了良好的分类性能，但是，由于工作条件的变化和环境噪声的干扰，训练数据和测试数据经常属于不同的分布，特征空间也不相同[103]。迁移学习(transfer learning,TL)能够将源域知识迁移至目标域，为跨域、小样本条件下应用深度学习进行轴承复合故障诊断提供了一种途径。

Liang 等[104]将生成对抗网络（GANs）与CNN结合，成功进行了轴承复合故障诊断。如图10（a）所示，首先使用小波变换提取原始信号的时频图像特征，将其分为训练集和测试集，通过GANs 生成虚假训练集，然后将真实和虚假训练集全部输入CNN 中进行模型训练，最后通过测试集验证复合故障检测的结果。图10（b）为提出的WT-GANCNN 方法与不采用虚假数据的WT-CNN 的诊断正确率对比图。可见，此方法正确率高、效果稳定。陈仁祥等[105]将子空间嵌入特征分布对齐方法用于故障诊断领域，实现了不同工况滚动轴承的复合故障诊断。训练样本为某一工况下的故障信号频谱，测试样本为其他工况下的信号频谱，将其输入迁移学习网络，利用KNN 对目标域数据的伪标签进行预测，获得最终分类器，实现了复合故障诊断。Chen 等[106]提出了一种基于任务特征学习网络和领域对抗训练技术的新兴领域对抗迁移网络（DATN）复合故障诊断框架。该方法利用2 个集成深度CNN 的非对称编码网络分别学习源域和目标域的特征表示，将源域有标签数据中学习到的网络权重转移到目标域指导训练，最后，引入具有反向标签损失的领域对抗训练来最小化源域和目标域分布差异。

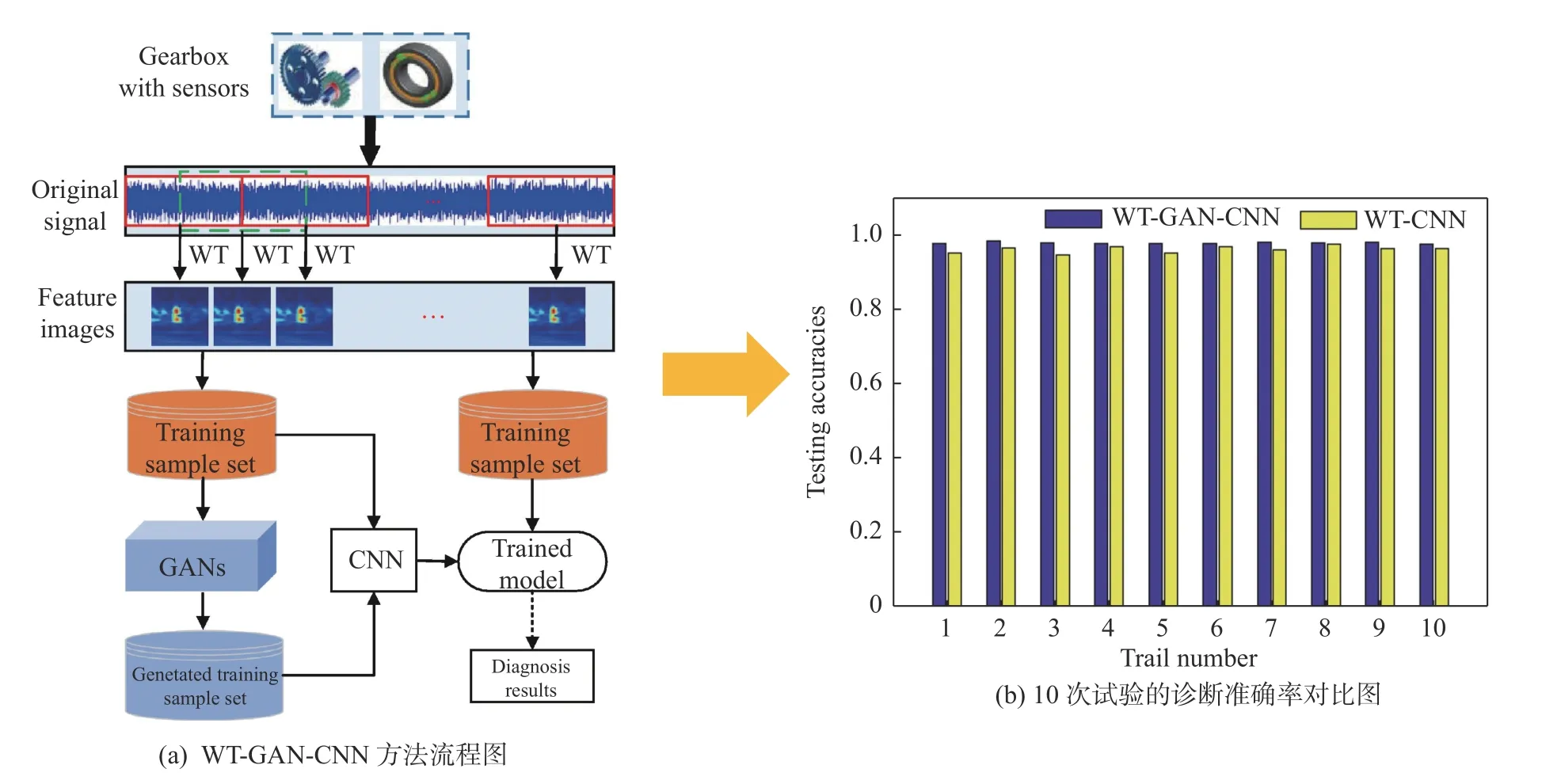
图10 WT-GAN-CNN 方法诊断流程及结果图[104]Fig.10 Diagnosis process and result diagram of WT-GAN-CNN method[104]

迁移学习的本意是为了节省人工标注样本的时间成本，使模型根据已标注数据向未标注数据迁移。对于一些新的故障问题，在样本量小的情况下利用已有的诊断知识，能够在短时间内快速适应数据的变化，从而使故障诊断成为可能。然而，在实现迁移学习过程中，经常会产生负迁移学习现象，现有方法往往通过控制局部均值差异来抑制这种现象，效果有时不够理想。

4 总结与展望

4.1 总结

由上述分析可知，滚动轴承复合故障的难点主要有3 方面。

1）原始振动信号的背景噪声干扰。一般来说，采集到的原始振动信号由于传递路径的影响，会包含许多如随机冲击和高斯噪声之类的背景噪声。因此，有必要对收集到的振动信号进行降噪处理，增强故障特征，为之后的故障特征分离和提取奠定基础。

2）复合故障种类多，数据获取困难。目前，学者们提出的方法都是针对某种或几种故障形式提出的，对所研究故障类型诊断效果优秀的方法对于其他类型的故障可能并不适用。现有的研究大多是基于仿真和台架试验数据来进行的，数据的可靠性得不到保障，将其运用于工程实际说服力不强。

3）复合故障之间相互耦合、相互干扰。复合故障并不是单故障简单叠加的结果，当多个复合故障强度不平衡时，弱故障可能被强故障所掩盖，造成漏诊。当2 个故障的故障特征频率比较接近时，如何在保留故障特征的同时分离出单个故障也是一个值得思考的问题。

目前，基于振动信号的滚动轴承复合故障诊断技术的思路，都是先进行复合故障特征的分离，然后进行单个故障特征的提取。其好处是可以借鉴轴承单个故障诊断领域的经验，诊断的实际效果比较可观。针对本文所述的7 种主要复合故障诊断技术，进行总结如下。

1）经验模态分解及其衍生方法。该类方法是常用的时频分析方法。它不仅擅于处理非平稳信号，而且能够根据信号特性进行自适应分解。但是，当故障成分频率接近、故障特征相互干扰时，采用此类方法进行信号分解容易产生模态混叠效应以及虚假分量。

2）小波变换。该方法可以提取振动信号不同频带上的能量特征，具有较好的自适应性和灵活性，但是其小波基函数的自适应选取和强噪声下的鲁棒性仍有提升空间。此外，WT 还存在频谱混叠问题。

3）经验小波变换。该方法能够自适应地选取一组小波滤波器来提取调幅调频信号，有效克服了EMD 存在的模态混叠的缺陷，适用于非线性非平稳信号的处理。然而，EWT 的关键在于频谱的划分，局部极大值个数及位置的选择都会影响最终的信号处理效果。如何根据不同信号的特点进行自适应的频谱分割，是EWT 方法改进的主要思路。

4）盲源分离。该方法能依据采样信号估计源信号，在混叠信号分离方面具有独特的优势。基于ICA 的盲源分离算法能够从混合信号中分离出具有统计独立性的分量，在滚动轴承复合故障中应用较多。虽然盲源分离已经在故障诊断领域内得到了蓬勃发展，但是在理论和算法方面依然存在完善空间。

5）共振解调。该方法通过确定不同的故障激发的共振频带实现故障特征的分离和提取，其改进方法较多。但是基于谱峭度的共振解调方法对随机脉冲十分敏感，在强噪声干扰下的诊断效果并不理想。

6）解卷积。该方法能提取感兴趣的周期性脉冲，与轴承故障特征十分契合，并且能在信噪比较低的情况下提取出周期冲击成分。解卷积方法主要应用有MCKD 和MOMEDA。MCKD 的特征提取效果取决于相关参数的选取。MOMEDA 主要缺点在于需要故障脉冲信号周期的先验知识。

7）智能诊断技术。该方法可以在极少的人工参与下实现复合故障特征的自适应提取，完成端到端的轴承复合故障诊断。它的缺点在于诊断效果一般取决于数据集的质量高低。大量高质量的标记数据可以提高其诊断准确率。

4.2 展望

由于轴承复合故障数据存在种类多、数据量大的特点，基于数据驱动的诊断技术将是未来的发展趋势。5G 时代的到来会推进实时故障诊断的发展，未来的复合故障诊断技术的诊断效率将会是衡量其性能优劣的一个重要指标。基于深度学习和迁移学习的故障诊断算法由于具有深度框架和高维特征提取能力，将会得到长足的发展。数字孪生理论将物理实体和多物理场虚拟实体完美统一，成为轴承复合故障精准诊断的最新研究方向和未来主战场。综上所述，硬件设备算力的提升和各类学科的发展应用，会推动各类诊断算法不断优化，使得轴承复合故障诊断领域的研究不断深入。