3DP 工艺中阶梯误差与渗透误差相互作用研究

2024-01-20杨伟东马千朝刘志越王媛媛朱东彬

天津大学学报(自然科学与工程技术版) 2024年3期

杨伟东，马千朝，刘志越，王媛媛，朱东彬

(1.河北工业大学机械工程学院，天津 300103；2.国家技术创新方法与实施工具工程技术研究中心，天津 300401)

三维打印(three-dimensional printing，3DP)工艺的通用文件格式为STL(stereolithography)模型，由大量离散的三角面片逼近实体模型，在逼近过程中存在一定的误差，只能近似表达实体模型的几何信息.在打印前需要对STL 模型进行分层，从而得到二维的轮廓信息，而在分层过程中会产生阶梯效应.

为了减小阶梯误差、提高打印精度，国内外学者针对影响阶梯误差的主要因素(成型方向和分层厚度)进行了大量研究.Li 等[1]使用基于梯度的优化算法实现分层方向和结构拓扑的优化.文献[2-5]通过建立多目标优化模型，使用改进的启发式算法最小化阶梯误差得到成型方向的最优解.罗楠等[6]针对复杂模型提出基于最小二乘的主成分分析算法，以阶梯误差最小的方向作为分层方向.文献[7-8]直接对计算机辅助设计(computer aided design，CAD)模型进行分层，避免了STL 模型在拟合CAD 模型时产生的误差.文献[9-10]以三角面片特征建立的数学模型为分层依据，通过自适应分层算法弱化阶梯效应.

3DP 工艺中黏结剂引起的渗透误差同样是影响打印精度的一个重要因素.基于3DP 工艺的打印样件x 和y 方向尺寸误差较小，而z 方向尺寸误差较大[11].马旭龙[12]针对黏结剂在砂床中渗透形成的最小单元体在x、y、z 方向上的各项异性误差，给出了黏结剂渗透误差的计算公式.杨伟东等[13]将3DP 工艺中黏结剂渗透误差在二维平面分解为xy 方向和z 方向两个分量，假设这两个方向上误差分量互不影响，通过打印实验标定了两个方向的渗透误差分量，以此对打印模型进行补偿.

对于STL 模型分层产生的阶梯误差，国内外相关的研究比较成熟，并且对于3DP 工艺黏结剂渗透误差，也有学者给出了渗透误差的计算和补偿方法.但针对3DP 工艺中阶梯误差与黏结剂渗透误差的相互作用，现有的研究相对欠缺.本文通过研究阶梯误差和黏结剂渗透误差的相互作用关系，提出了将这两项误差进行合成的计算公式.

1 3DP工艺原理性误差研究

1.1 阶梯误差研究

STL 模型的分层平面如图1 所示，本文将法向量方向与成型方向夹角大于90°的三角面片称为向下三角面片，其对应分层所产生的阶梯误差称为正阶梯误差；法向量方向与成型方向夹角小于90°的三角面片称为向上三角面片，其对应分层所产生的阶梯误差称为负阶梯误差.

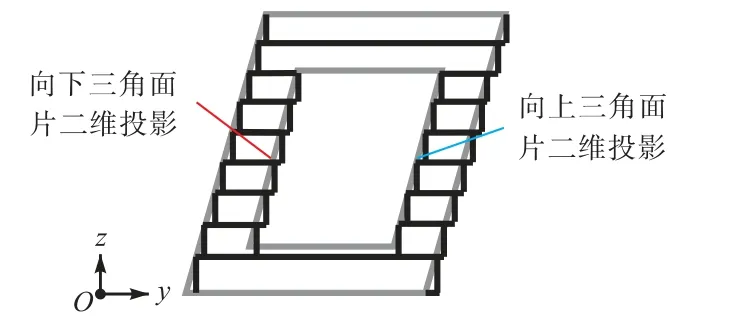
图1 二维分层平面Fig.1 Two-dimensional layered plane

1.2 黏结剂渗透仿真数学模型

1.2.1 黏结剂渗透形态仿真实验

本文以Gao 等[14]建立的多层渗透仿真模型为基础，使用COMSOL 软件建立黏结剂从喷出到渗入砂床的数学模型，在二维平面进行黏结剂渗透仿真实验.将由喷嘴喷射黏结剂撞击砂床位置起始层和最终层的最外侧连线作为三角面片的二维投影，即模型的理想打印轮廓，将黏结剂渗透后黏结砂粒形成的实际边界作为打印轮廓.

为了建立黏结剂渗透仿真模型，采用圆形润湿壁代替实际砂粒形状，砂床的模拟采用砂粒平均半径r为71.4 μm，砂床的孔隙率为0.395 4.阵列式喷头的喷嘴形状和尺寸由某厂家提供，喷嘴为倒梯形，其上底为 54 μm、下底为 50 μm、高度为 50 μm.在COMSOL 软件两相流模块中设置1 个喷头，用于在二维平面模拟阵列式喷头，该喷头包含28 个喷嘴，喷嘴间距为76 μm.

使用呋喃树脂作为黏结剂，其物性参数如表1 所示.为了准确模拟黏结剂液滴在砂层中渗透，黏结剂与砂粒的接触角应小于π/4.呋喃树脂与砂粒之间接触角约为31.7°，因此在边界条件中设置接触角为π/6.渗透仿真模型边界条件设置如表2 所示，其中PP0 为周期性变化的压力脉冲信号.

表1 呋喃树脂物性参数Tab.1 Furan resin property parameters

表2 仿真模型边界条件Tab.2 Boundary conditions of simulation model

理想情况下仿真中不同三角面片二维投影对应黏结剂的渗透形态如图2 所示.图2(a)为向上三角面片二维投影仿真实验的理想渗透形态，图2(b)为向下三角面片二维投影仿真实验的理想渗透形态.灰色部分为黏结剂渗透后砂粒的黏结区域，z 为成型方向，F1、F2为三角面片的法向量方向.

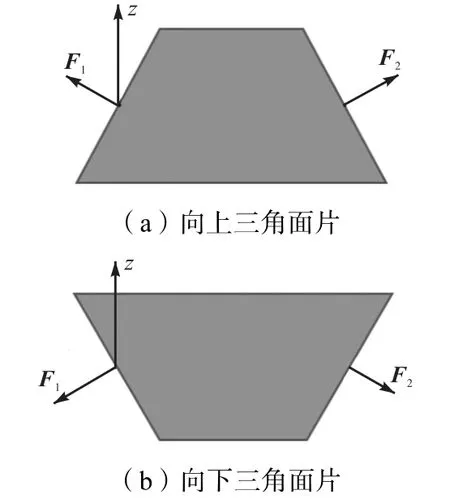
图2 三角面片二维投影理想仿真结果Fig.2 Ideal simulation results for the two-dimensional projection of triangular patches

1.2.2 渗透形态仿真实验分析

为了对模型的理想打印轮廓和实际打印轮廓的位置误差进行定量分析，通过控制喷嘴喷射行为进行不同角度三角面片二维投影的渗透仿真实验，其中向上三角面片的部分仿真结果如图3 所示.以三角面片二维投影与水平面所夹锐角为理想斜面角度，两侧斜面角度均为25°的情况如图3(a)所示，左右两侧斜面角度分别为65°和55°的情况如图3(b)所示.图中红色区域为空气，蓝色区域为黏结剂液滴，白色圆形区域为砂粒结构.

图3 不同角度渗透仿真Fig.3 Simulation of infiltration at different angles

通过测量不同角度三角面片二维投影的渗透仿真结果，得到理想打印轮廓与打印轮廓的位置误差，结果如表3 所示.以三角面片法向量方向向上的位置误差为正值，反向为负值.其中理想斜面角度为0°时，其向上三角面片无位置误差，其向下三角面片的位置误差为z 方向的渗透误差；理想斜面角度为90°时，其三角面片的位置误差为xy 方向的渗透误差.

将仿真实验中的理想斜面角度转换为三角面片法向量方向与成型方向夹角.当夹角在0°～90°范围为向上三角面片，夹角角度增加，负阶梯误差在数值上逐渐增大，位置误差也逐渐增大，可以看出渗透误差对阶梯误差具有补偿作用.当理想斜面角度为25°时，向上三角面片的位置误差为负值，体现了负阶梯误差对三角面片位置误差的影响.当夹角在90°～180°范围为向下三角面片，夹角角度增加，正阶梯误差逐渐增大，位置误差也逐渐增大，此时阶梯误差与正渗透误差相互叠加.

通过分析理想打印轮廓与实际打印轮廓之间的位置误差，考虑阶梯误差与渗透误差对打印精度的综合影响，本文将二者相互作用的合成误差称为与三角面片法向量方向相关的三角面片偏移误差，即模型打印后三角面片的理论位置与其实际位置之间的位置误差.

2 三角面片偏移误差公式的建立

2.1 三角面片偏移误差公式原理

不考虑阶梯误差与渗透误差之间的相互作用时，斜孔的三角面片打印产生的阶梯误差和渗透误差在二维平面如图4、图5 所示.设定z 轴正方向为成型方向，f 为三角面片法向量方向.由于黏结渗透形成的最小单元体在打印平面近似为圆形，认为黏结剂的渗透误差在水平方向上近似相同，记为 dxy，z 方向的渗透误差分量记为 dz.h 为分层厚度，θ为三角面片法向量方向与成型方向的夹角.图中灰色直线为三角面片的二维投影，红色虚线为实际的打印轮廓.定义红色虚线与灰色实线之间的距离为三角面片二维投影和实际打印轮廓之间的偏移误差Δ，Δ1为向下三角面片的偏移误差，Δ2为向上三角面片的偏移误差.

图5 向上三角面片偏移误差二维示意Fig.5 Two-dimensional schematic diagram of the upward triangular patch offset error

三角面片偏移误差Δ的计算可分为两类.

(1) 当0<θ≤π/2时，以向上三角面片的偏移误差进行计算.从图5 中可以看出xy 方向渗透误差分量 dxy使斜面产生了偏移，而阶梯误差对实际打印边界并无影响.因此该偏移误差为

(2) 当π/2<θ<π 时，以向下三角面片的偏移误差进行计算.从图4 可以看出阶梯误差和渗透误差都对斜面的偏移产生了影响，同时考虑xy 方向和z 方向渗透误差计算得到的偏移误差为

在不考虑阶梯误差和渗透误差之间的相互作用时，三角面片的偏移误差公式为

通过渗透仿真实验可知阶梯误差和黏结剂的渗透误差之间存在相互作用.因此，式(1)不能作为三角面片偏移误差的计算公式，需要进一步考虑这两项误差的相互作用.

由于阶梯误差与三角面片的法向量方向和分层厚度有关，分层厚度为z 方向上的分量.考虑相互作用的向上三角面片偏移误差公式等效为Δ(θ)=dxysinθ−d1cosθ；考虑相互作用的向下三角面片偏移误差公式等效为Δ(θ)=dxysinθ−d2cosθ.因此，阶梯误差和渗透误差相互作用的三角面片偏移误差公式为

式中：d1为向上三角面片中负阶梯误差与渗透误差之间的相互作用系数；d2为向下三角面片中正阶梯误差与渗透误差之间的相互作用系数.d1、d2为无量纲的变量.

2.2 三角面片偏移误差公式参数标定实验

通过测量不同法向量方向三角面片的偏移误差进而标定式(2)中的未知参数，设计样件模型如图6所示.样件外观为长方体，尺寸大小为600 mm×140 mm×10 mm，长方体内部有多个角度的平行斜面，斜面与水平方向夹角依次为90°、80°、70°、60°、50°、40°、30°、20°.图6(a)为样件1 的STL 模型，图6(b)为样件2 的STL 模型.如图6 所示，样件1 棱上表面和棱下表面为一组平行斜面，样件2 孔上表面和孔下表面为一组平行斜面.通过镜像翻转模型验证三角面片偏移误差只与法向量方向和成型方向的夹角相关，得到样件1 和样件2 的镜像模型为样件3 和样件4.

图6 参数标定实验样件STL模型Fig.6 STL model of the experimental sample for parameter calibration

4 个样件采用某厂家设备按照层厚为0.3 mm、z方向为成型方向进行打印，得到打印样件如图7(a)所示.采用形创公司的HandySCAN3D 手持式三维激光扫描仪扫描所有打印样件，得到样件点云模型，以样件1 的扫描模型为例，点云模型修复后的STL模型如图7(b)所示.

图7 样件扫描模型Fig.7 Model of the sample by scan

测量样件1、样件3 打印模型与设计模型内部棱上表面和棱下表面的位置误差，棱上表面的位置误差为向上三角面片的偏移误差，棱下表面的位置误差为向下三角面片的偏移误差；测量样件2、样件4 打印模型与设计模型内部孔上表面和孔下表面的位置误差，孔上表面的位置误差为向下三角面片的偏移误差，孔下表面的位置误差为向上三角面片的偏移误差.

使用三维模型设计软件Magics 对扫描模型与设计模型进行位置拟合，观察表面的尺寸误差分布.样件的扫描模型与设计模型的误差对比如图8(a)～(d)所示，图8(e)为颜色信息对应的误差大小.图中样件1 与样件3 的三角面片偏移误差变化趋势一致，样件2 与样件4 的三角面片偏移误差变化也有良好的一致性，打印所得砂型法向量方向与成型方向夹角相同的三角面片的偏移误差近似相同.向上三角面片偏移误差随着斜面与水平面夹角角度的减小而减小；向下三角面片偏移误差随着斜面与水平面夹角角度的减小而增大.尺寸误差分布规律符合渗透形态仿真实验的结果分析.

图8 尺寸误差信息Fig.8 Variation in dimensional error

使用三维检测与计量软件Geomagic Control X测量样件扫描模型与设计模型的三角面片偏移误差.以三角面片所在平面与水平面所夹锐角α为测量角度，测量结果如表4 所示.

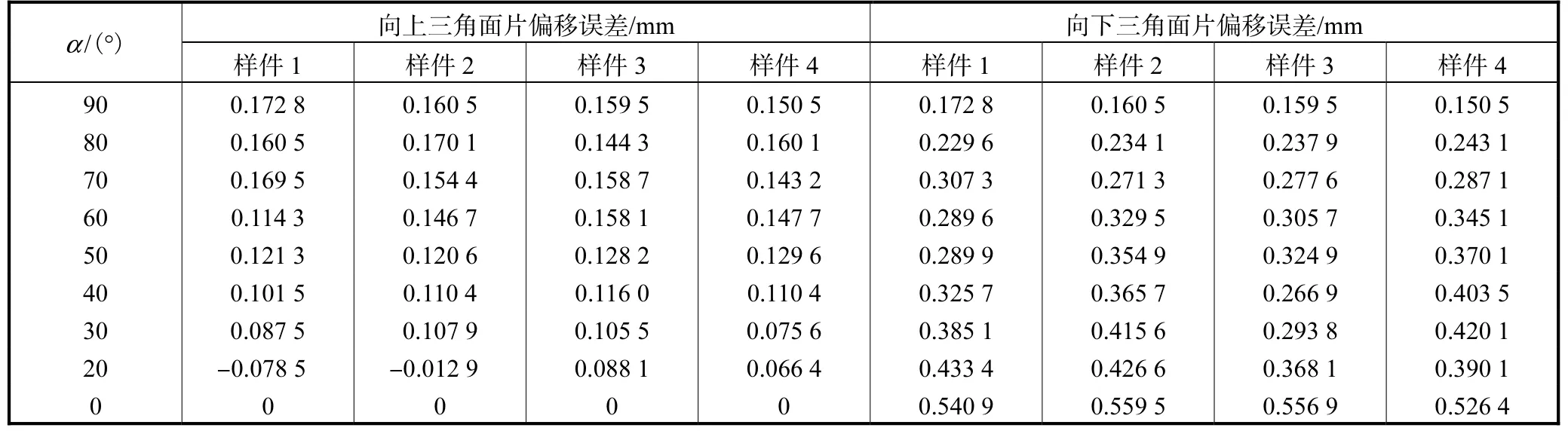
表4 样件扫描模型三角面片偏移误差Tab.4 Triangular patch offset error of the sample scanning model

根据表4 给出的三角面片偏移误差实际测量值对式(2)中的未知参数进行标定，首先将表中的测量角度α转化为三角面片法向量方向与成型方向的夹角θ，对于θ＝90°的三角面片偏移误差记为 dxy，θ＝180°的三角面片偏移误差记为 dz.本文假设不同角度的向上或向下三角面片在打印时渗透误差与阶梯误差作用系数相同，然后将其他角度三角面片偏移误差数据代入式(2)中基于最小二乘法计算 d1和 d2两个参数.计算得到 d1的最大值为 0.052 7，最小值为-0.022 9，d2的最大值为0.392 5，最小值为0.289 6.计算所得的未知参数 d1、d2数值都在一定范围内变化.

取所有样件相互作用系数的平均值标定公式中未知参数.通过计算得到的4 个未知参数分别为：dxy＝0.160 8 mm；dz＝0.595 9 mm；d1＝0.007 2；d2＝0.347 6.将此4 个参数代入式(2)中得到标定参数后的三角面片偏移误差公式，可计算不同角度θ的三角面片偏移误差.

将表4 中的不同测量角度带入标定参数后的公式，由式(2)计算的三角面片偏移误差与实测三角面片偏移误差对比如图9 所示.从图中可以看出，式(2)计算得到的误差和实测误差变化趋势一致.为了进一步说明该公式预测三角面片偏移误差的有效性，对三角面片偏移误差公式计算值与实际测量值之差的绝对值进行分析.计算误差在0.100 mm 范围内，最大值为0.060 mm，最小值为0.002 mm，平均变化率在1.7%左右，可满足工艺的需求.

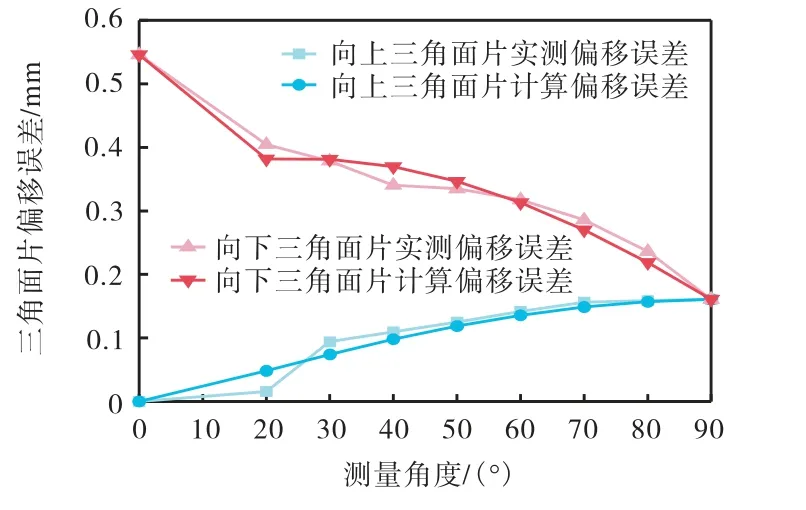
图9 参数标定实验公式计算值和实际测量值对比Fig.9 Comparison between the calculated value of the parameter calibration experimental formula and the actual measured values

3 三角面片偏移误差公式实验验证

为验证标定参数后的式(2)计算其他角度三角面片偏移误差的有效性，分别将样件1 和样件2 的模型绕y 轴顺时针旋转5°，样件3 和样件4 的模型绕y 轴逆时针旋转5°.模型旋转后的斜面与水平面所夹锐角角度依次为 85°、75°、65°、55°、45°、35°、25°、15°.仍设置层厚为0.3 mm，z 方向为成型方向进行打印.使用形创公司的HandySCAN3D 扫描打印样件，部分样件的扫描模型如图10 所示.