考虑蠕变三阶段的哈氏合金X 蠕变-疲劳裂纹扩展模拟

张俊红 ，李哲华，林杰威，于洋洋，戴胡伟

(1.天津大学先进内燃动力全国重点实验室，天津 300354；2.天津仁爱学院机械工程学院，天津 301636)

为提升工作效率和推重比，航空发动机工作温度以每年19 ℃的速率迅速上升，这给航空发动机热端部件的可靠性提出了越来越高的要求.燃烧室是航空发动机的关键热端部件，服役中启停工况下的非均匀温度场载荷会引起热应力，由此产生的疲劳损伤以及稳态工况下热应力长期保持引起的蠕变损伤的共同作用是引起燃烧室开裂失效的主要原因.哈氏合金X 是一种固溶强化的镍基合金，在高温下强度高且具有优异的加工性能以及抗蠕变、抗氧化和抗腐蚀性能[1-2]，被广泛用作民航发动机燃烧室基体材料.

为探索蠕变-疲劳作用下的哈氏合金X 裂纹扩展行为与损伤机理，国内外学者开展了大量实验研究.Hour 等[3]观察到在650 ℃下，哈氏合金X 的疲劳和1 min 保载的蠕变-疲劳裂纹均表现为穿晶模式增长；Lee 等[4]通过对拉伸试样的断裂面的评估，确定了哈氏合金X 在低循环疲劳下，随着温度和保载时间的增加，断裂模式逐渐从穿晶断裂转向沿晶断裂，导致寿命缩短.Yoon 等[5]观察到760 ℃和870 ℃下哈氏合金X 的疲劳裂纹开始为穿晶模式，后以穿晶和沿晶混合模式生长.

可通过实验方法对不同载荷条件下的宏观裂纹扩展速率及材料微观小裂纹、孔洞微观演变行为进行测试表征，但是在裂纹扩展过程中，疲劳载荷、蠕变载荷对裂纹扩展过程中损伤累积的贡献未得到量化.为此，学者们提出了结合有限元和损伤力学的裂纹扩展过程数值计算方法.Wen 等[6]提出了考虑材料中孔洞的聚集和微裂纹发展的蠕变损伤模型，并使用单元失效技术在316 H 不锈钢的裂纹扩展模拟中得到验证；Wu 等[7]使用内聚力模型模拟了21-6-9 奥氏体不锈钢二维平面的裂纹扩展；Ahmad 等[8]基于扩展有限单元法建立了蠕变断裂起始和裂纹扩展模型.

建立准确的损伤模型是进行裂纹扩展有限元模拟的关键.Hosseini 等[9]提出了一种考虑应力变化影响的蠕变损伤模型，并应用于1CrMoV 的裂纹扩展模拟中，但该模型需要拟合的参数过多，可能导致误差较大.Haque 等[10]使用SIN-HYPERBOLIC 模型模拟了648.9～982.2 ℃(1 200～1 800 ℉)下哈氏合金X的蠕变裂纹损伤累积过程，但该模型中参数φ 的拟合受应力影响，实际应用存在局限性.Liu 等[11]对哈氏合金X 进行了816 ℃下的蠕变-疲劳裂纹扩展模拟，并量化了蠕变、疲劳和相互作用的损伤贡献，但其蠕变损伤公式仅考虑了蠕变第Ⅱ阶段.Tang 等[12]对G115 的蠕变-疲劳裂纹扩展模拟以及Lai 等[13]对蠕变裂纹尖端应力场估算同样仅考虑了蠕变第Ⅱ阶段.Jing 等[14]对P91 以及Wang 等[15]对UNS N10003的裂纹扩展模拟忽略了蠕变第Ⅰ阶段.

从上述研究来看，现有的研究中主要考虑蠕变第Ⅱ阶段对蠕变-疲劳损伤的影响，但有研究表明，镍基合金的蠕变第Ⅲ阶段占比通常较大[16]，并且在不同温度、载荷条件下，蠕变各阶段的占比也会有所不同，蠕变各阶段对损伤累积的贡献有待进一步探讨.本文推导了考虑蠕变3 个阶段的蠕变本构模型，进行了哈氏合金X 在650 ℃蠕变-疲劳裂纹扩展过程数值计算，分析了纯蠕变条件下蠕变不同阶段对裂纹扩展的影响，量化了蠕变-疲劳交互作用下蠕变、疲劳和交互损伤占比，并讨论了蠕变-疲劳交互作用下载荷幅值、保载时间等因素对损伤占比的影响.本研究对于指导服役条件下的燃烧室疲劳强度设计具有较大的工程意义，对于揭示哈氏合金X 在蠕变-疲劳载荷交互作用下的损伤机理具有较大的科学意义.

1 蠕变-疲劳损伤模型

1.1 蠕变本构模型

如图1[17]所示，材料的蠕变过程可分为初始蠕变阶段(第Ⅰ阶段)、稳定蠕变阶段(第Ⅱ阶段)和加速蠕变阶段(第Ⅲ阶段).蠕变第Ⅰ阶段本构模型可以用应变硬化定律[18]来表示，公式定义为

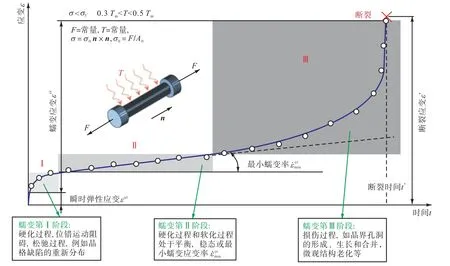
图1 典型金属材料蠕变曲线Fig.1 Creep curve of typical metal materials

式中：A1、n1和p 为材料参数；εc,pri和εc,tol分别为第Ⅰ阶段蠕变应变和总蠕变应变；σeq为等效应力.

工程上主要考虑蠕变第Ⅱ阶段对损伤累积的影响，可通过诺顿幂律蠕变模型描述，其公式为

式中：εc,sec为第Ⅱ阶段蠕变应变；A 和n 为材料参数.

结合式(1)和(2)，得到考虑了蠕变第Ⅰ和第Ⅱ阶段的蠕变本构模型，具体如下：

式中：εc,ij为蠕变应变张量；Sij为偏应力张量.

Liu 等[19]提出了考虑到蠕变第Ⅱ和第Ⅲ阶段的多轴蠕变本构模型，该模型基于微观力学，可以显著改善损伤的定位和网格的独立性，具体如下：

式中：σ1为最大主应力；ωc为蠕变损伤.式(4)中的(σ1/σeq)2项会导致模拟过程中裂纹尖端的应力过度松弛，Wen 等[6]考虑到空腔增长和微裂缝的相互作用，提出了一个新的蠕变构成方程以解决此问题，定义如下：

结合式(3)和(5)，得到考虑了蠕变3 个阶段的蠕变本构模型，表达式如下：

本文分别使用考虑第Ⅱ阶段的蠕变本构(式(2))，考虑第Ⅰ、第Ⅱ阶段的蠕变本构(式(3))，考虑第Ⅱ、第Ⅲ阶段的蠕变本构(式(4))，考虑第Ⅰ、第Ⅱ、第Ⅲ阶段蠕变本构(式(6))描述蠕变过程，对比分析蠕变不同阶段对哈氏合金X 蠕变-疲劳裂纹扩展过程中损伤累积的影响.

1.2 蠕变损伤模型

本文使用延性耗竭模型计算蠕变损伤.蠕变延性耗竭模型认为，当材料的累积应变达到该状态下的蠕变延性时材料失效[20].在本研究中，蠕变损伤率通过蠕变应变率和蠕变延性计算，定义如下：

式中：εf为单轴蠕变延性；σm为静水应力.

通过积分得到蠕变损伤计算式为

式中th为保载时间.

1.3 疲劳损伤模型

基于Lemaitre 等[21]的损伤方程和Ostergren[22]的净拉伸滞后能方程，得到低循环疲劳中的损伤累积模型为

式中：ωf为疲劳损伤；Nf为失效循环数；σmax和Δεp分别为每加载循环中的最大应力和塑性应变范围；q、C1和β 为材料参数.

考虑到材料循环硬化或软化的影响，塑性循环应变范围是由循环应力-应变关系得出，即

式中：σΔ 和σmin分别为应力范围和最小应力；K′和n′为从低循环疲劳试验中获得的材料参数.

此外，Lemaitre[23]提出了一个三轴系数来描述多轴应力对疲劳损伤累积的重要影响，定义为

式中ν 是泊松比.在单轴加载情况下Rν= 1.

因此，考虑到应力三轴性的影响，低循环疲劳损伤累积公式表示为

1.4 蠕变-疲劳交互损伤模型

裂纹扩展在蠕变-疲劳交互载荷作用下，由于其蠕变孔洞和疲劳裂纹的相互促进作用，将纯蠕变损伤和纯疲劳损伤线性相加不足以表示真实的蠕变-疲劳交互损伤情况.本研究使用修正的Skelton 等[24]的蠕变损伤和疲劳损伤非线性叠加总损伤方程描述蠕变-疲劳的交互，具体如下：

式中ω为总损伤值.

2 有限元仿真

2.1 有限元模型

根据《ASTM E2760-19》[25]，本研究使用W＝30 mm、初始裂纹长度a0＝10.5 mm 的CT 试样进行计算，具体的几何图形和尺寸如图2 所示.为了减少计算时间、简化模型，考虑载荷及几何的对称性，使用1/4 的CT 试样三维模型进行计算模拟.

图2 CT试样的几何形状与尺寸(单位：mm)Fig.2 Geometry and dimensions of the CT specimen used for simulation(unit：mm)

在裂纹尖端部位使用尺寸为100µm×100µm 的细化网格，其他区域使用较大网格，并用梯形单元连接过渡；使用八节点三维减缩积分单元(C3D8R)进行网格划分，如图3 所示，模型网格总数为21 180.在裂纹扩展平面上使用对称边界条件约束；在垂直于厚度方向和裂纹扩展平面的一面上使用对称边界条件.在CT 试样孔中心设置了一个参考点，通过多点约束(MPC)将其参考点与孔的内表面一侧进行耦合，对参考点施加载荷，模拟实际裂纹增长实验中销轴对CT 试样的加载过程.对参考点施加的循环载荷如图4 所示，加载和卸载时间均为固定的0.5 s.定义梯形波的载荷比为

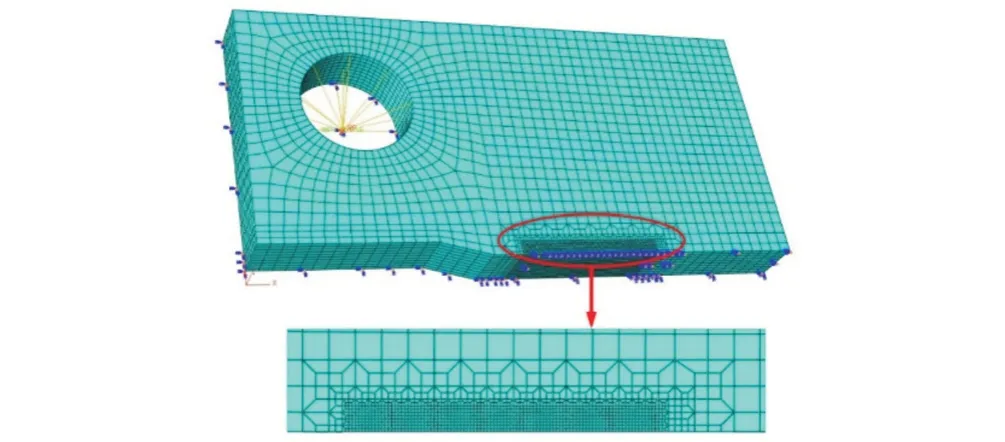
图3 CT试样有限元模型Fig.3 Finite element model of CT specimen

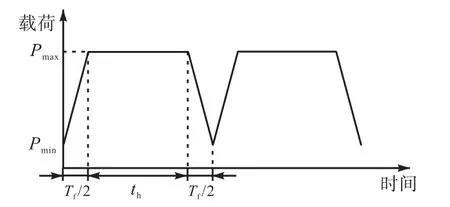
图4 循环加载示意Fig.4 Schematic of the applied cyclic loading

式中Pmin和Pmax分别为最小载荷和最大载荷.

2.2 数值模拟方法以及参数

本研究中裂纹增长模拟由ABAQUS 实现，使用CREEP 子程序定义蠕变变形本构关系，通过基于Fortran 语言的二次开发USDFLD 子程序计算蠕变损伤、疲劳损伤和蠕变-疲劳交互损伤.在有限元模拟加载循环过程中，对计算域中每个单元损伤、循环损伤值进行累积计算，当累积损伤达到1 时，认为该单元失效，单元所处位置产生裂纹，并通过控制场变量删除该单元，描述前序加载循环中裂纹演变对下一加载循环中应力及损伤累积的影响.所删除单元区域即为裂纹扩展区域.

本文研究对象为哈氏合金X，化学成分见表1.根据《ISO 6892-1：2016》进行650 ℃下的单轴拉伸试验，得到的哈氏合金X 真实应力-应变曲线如图5所示，蠕变参数A、n、A1、n1和p 由哈氏合金X 在650 ℃下的单轴蠕变试验[26-28]确定.疲劳参数从哈氏合金X 在相同温度下的供货厂商提供的低周疲劳试验中获得，所有损伤模型的参数如表2 所示.

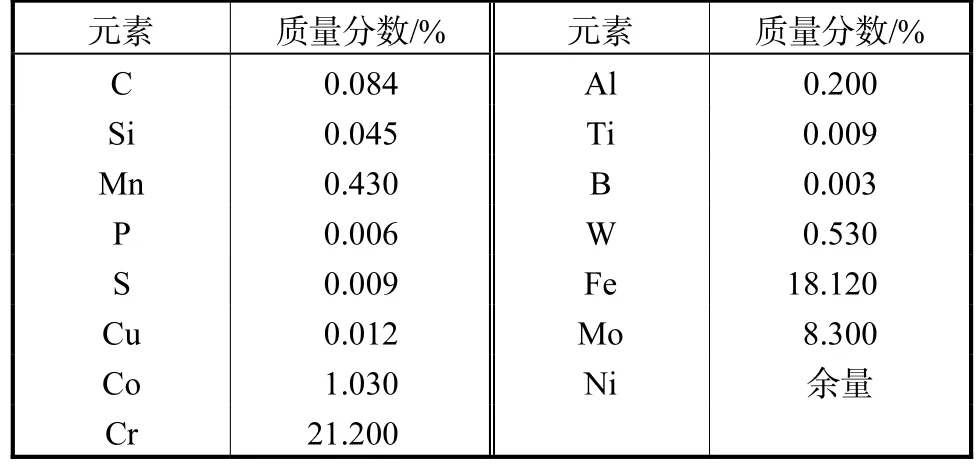
表1 哈氏合金X化学成分Tab.1 Chemical composition of the Hastelloy X

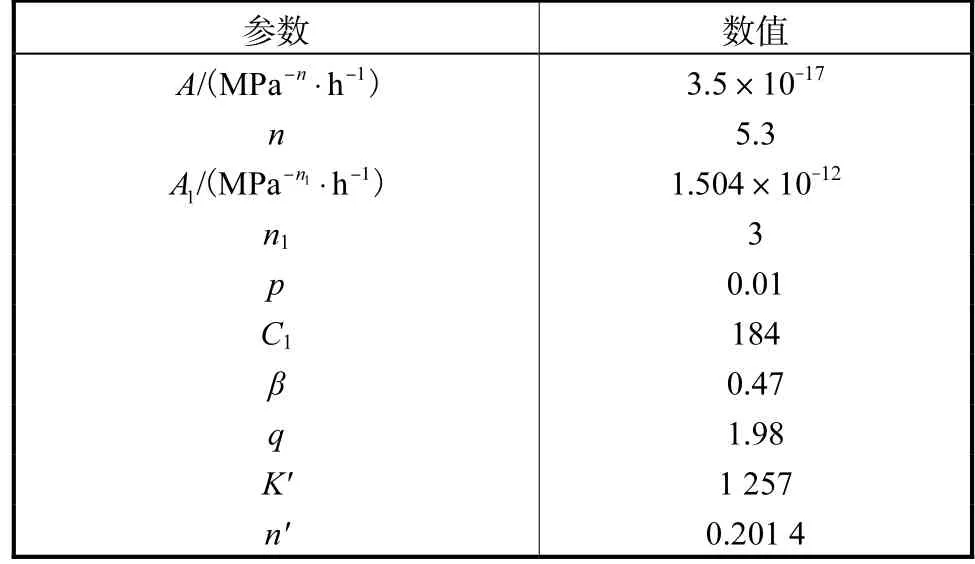
表2 损伤模型材料参数Tab.2 Material parameters for the damage models

图5 哈氏合金X 650 ℃下的真实应力-应变曲线Fig.5 True stress-strain curve of Hastelloy X at 650 ℃

2.3 断裂力学参数

针对纯蠕变、纯疲劳和蠕变-疲劳载荷条件，使用与时间无关和与时间有关的两类断裂力学参数进行分析.由线性弹性理论定义的应力强度因子K 包含了试样的应力和几何信息，纯疲劳裂纹扩展结果一般用裂纹尖端应力强度因子范围ΔK 来表示.在纯蠕变和蠕变-疲劳条件下，ΔK 可用于蠕变脆性材料.根据《ASTM E2760-19》[25]标准，K 的计算方法如下：

式中：B、W 和a 分别为CT 试样的厚度、宽度和裂纹长度；P 是施加在CT 试样上的载荷.对于蠕变韧性材料，一般使用随时间变化的参数Ct,avg，即

式中：ΔVc为每个载荷周期中保载时间内的蠕变载荷位移；E 和E'分别是弹性模量和有效弹性模量；ν 是泊松比.

3 结果与讨论

3.1 有限元仿真的验证

为了验证所提出的本构模型、损伤模型和相应的材料参数的准确性，将哈氏合金X 在650 ℃时纯蠕变、纯疲劳和60 s 保载时间的蠕变-疲劳交互条件下的有限元分析结果和实验结果[3,26]进行对比，da/dt-Kmax和da/dN-ΔK 的对比曲线如图6 所示.实验数据根据Paris-power 定律进行拟合，如图6 中的实线所示，代表着裂纹稳定扩展阶段.同样，对于纯蠕变和60 s 保持时间的裂纹稳定扩展实验数据，使用式(23)进行拟合.

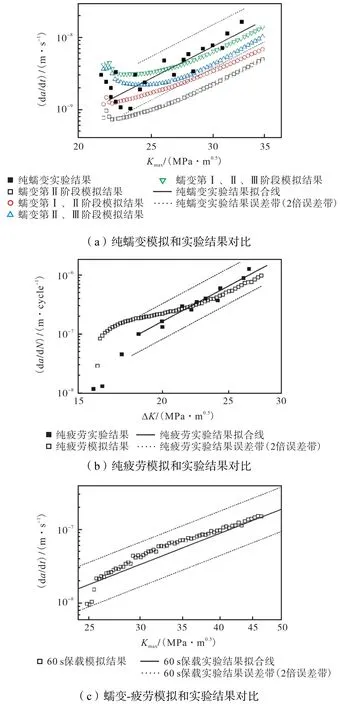
图6 裂纹扩展速率模拟与实验结果比较Fig.6 Comparison between simulation and experimental results of crack propagation rate

式中：f 为加载频率；C'和m'为拟合参数.Kmax的值在R＝0.05 情况下非常接近ΔK.

图6(a)显示了纯蠕变裂纹扩展的da/dt 和Kmax的关系，进行了4 种考虑蠕变不同阶段的纯蠕变模拟.由图可知考虑蠕变所有阶段的模拟结果与实验数据最贴合，裂纹稳定扩展的数据点都在2 倍误差带范围内，且模拟结果显示了一个勾状特征，这是应力松弛的结果[29-30].da/dt 的值最初很大，然后减少，之后随着Kmax的增加而增加.Saxena[31]和Yokobori[32]对这一现象的解释如下：高弹性应力最初导致裂纹尖端高速蠕变，随着时间的积累，裂纹尖端应力的重新分布导致应力松弛，蠕变速度下降.同时，由于Kmax的增加和应力松弛随时间的增加而减弱，裂纹的扩展速度加快.在裂纹扩展率的稳定增长阶段，考虑蠕变所有阶段的模拟结果和实验结果的斜率基本相同，数值的大小也很接近.这表明本文第1 节中提到的本构模型(式(6))和损伤模型可以准确预测蠕变裂纹增长.

纯疲劳裂纹扩展模拟结果和实验结果对比如图6(b)所示，两者在裂纹稳定扩展阶段的数值大小接近，趋势相同.在进入裂纹稳定扩展阶段之前da/dN值猛增，此时为裂纹萌生阶段.整体上看，使用损伤累积模型能够贴切地模拟疲劳裂纹扩展行为.图6(c)为60 s 保载下的模拟和实验结果对比，由于考虑三阶段的纯蠕变模拟结果最优，故使用本构模型式(6)进行蠕变-疲劳裂纹扩展模拟运算，模拟结果处于2 倍误差带内，且整体趋势与实验拟合线结果相符.

综上所述，应用本文提出的考虑蠕变三阶段的蠕变本构模型和损伤模型进行有限元模拟的结果与实验结果具有良好的一致性，验证了损伤公式、材料参数和模拟方法的可靠性，接下来将继续使用它们进行裂纹扩展的研究分析.

3.2 蠕变阶段对纯蠕变裂纹扩展的影响

考虑蠕变不同阶段的裂纹扩展模拟结果如图7所示.图7(a)展示了恒定载荷为5 kN、K0为33 MPa·m0.5下的纯蠕变裂纹扩展模拟结果，整体裂纹扩展速度由慢至快分别为仅考虑蠕变第Ⅱ阶段，考虑第Ⅰ和第Ⅱ阶段，考虑第Ⅱ和第Ⅲ阶段，考虑第Ⅰ、Ⅱ、Ⅲ 3 个阶段，这印证了蠕变第Ⅰ阶段和第Ⅲ阶段在图1 中的斜率均大于蠕变第Ⅱ阶段.随着Kmax的增加，4 种情况的da/dt-Kmax斜率趋于一致，考虑第Ⅰ阶段蠕变和其他条件一致，不考虑第Ⅰ阶段蠕变的裂纹扩展速度越来越接近，说明随着裂纹的生长，蠕变第Ⅰ阶段对裂纹扩展速率的影响越来越小.考虑第Ⅲ阶段的两种情况比另两种蠕变条件的整体速度更大，验证了考虑哈氏合金X 的蠕变第Ⅲ阶段的重要性.同时，从图中可以观察到，考虑到蠕变第Ⅲ阶段的曲线勾状特征更加明显，这是因为包含蠕变第Ⅲ阶段损伤公式中的指数函数项包含损伤项exp (ω3/2)，在加载初期由于应力集中，损伤增加较快，使得指数函数项变大、应变率变大，进而导致损伤率变快.图7(b)和图7(c)中恒定载荷为6 kN 和7 kN 的模拟结果规律也与此类似.当考虑蠕变第Ⅰ阶段结果和其他条件不变，不考虑第Ⅰ阶段的裂纹扩展速率非常接近时，第Ⅰ阶段即可近似忽略.第Ⅲ阶段同理.

图7 不同载荷下4 种蠕变阶段组合的纯蠕变裂纹扩展模拟结果(650 ℃)Fig.7 Simulation results of pure creep crack propagation for four combinations of creep stages under different loads(650 ℃)

为了量化各蠕变阶段对蠕变速率的影响，定义了一个无量纲变量δ，在相同Kmax值下，将考虑3 个蠕变阶段的裂纹扩展速率定义为基准值，计算其与其他情况下的模拟结果之差相对基准值的比值，即

式中：vx为考虑蠕变x 阶段的裂纹扩展速度；v123为考虑蠕变所有阶段的裂纹扩展速度.通过分析δx可知考虑蠕变第x 阶段相对考虑蠕变所有阶段的预测速率差异.如图8 所示，5 kN 载荷下，随Kmax的增大，δ2从0.80 减小至0.63；δ12由0.73 减至0.52，后逐渐增大至0.61；δ23由0.08 增至0.23，后减小至0.01，预测差异由大到小顺序为：考虑蠕变第Ⅱ阶段，考虑蠕变第Ⅰ、Ⅱ阶段，考虑蠕变第Ⅱ、Ⅲ阶段.这说明蠕变第Ⅱ和Ⅲ阶段为裂纹扩展模拟中的重要本构组成，由未考虑蠕变第Ⅲ阶段的两种模拟情况的预测差异的差距先增后减、最后趋于极小值0.02 可知，蠕变第Ⅰ阶段的影响在裂纹扩展前期相对后期更大，这是由于裂纹扩展后期的应力更大，蠕变第Ⅰ阶段在蠕变过程中对损伤贡献的占比远小于蠕变第Ⅱ和第Ⅲ阶段的贡献占比.同时可观察到，裂纹扩展前期的各差异值的变化幅度均大于后期，故未考虑完整蠕变阶段的裂纹扩展速率差异在裂纹扩展过程中是不断变化的，且前期相对后期的变化更剧烈.

图8 5 kN载荷下纯蠕变裂纹扩展δx 与Kmax 关系Fig.8 δx versus Kmax for pure creep crack propagation under a load of 5 kN

式中n 为δx对应的Kmax的取值个数.图9 为3 种载荷下模拟结果的2、12和23的对比.随着载荷增大，2由0.67 减至0.64，说明在本研究载荷大小范围内，考虑蠕变第Ⅱ阶段的裂纹扩展模拟结果的准确性随载荷增大略有提高；23由0.16 减小至0.07，这说明载荷越大，本构模型中考虑蠕变第Ⅱ和Ⅲ阶段的模拟结果准确性越高；12由0.57 增至0.61，即考虑蠕变第Ⅰ、Ⅱ阶段在小载荷情况下的准确性更大，载荷越大，蠕变第Ⅲ阶段对预测结果的准确性更加不可忽略.故不同载荷大小下，考虑蠕变不同阶段的预测差异不同，为了应对多种载荷情况，在本构方程中有必要考虑到蠕变所有阶段.

图9 纯蠕变裂纹扩展x 与载荷的关系Fig.9x versus load for pure creep crack propagation

3.3 载荷幅值对蠕变-疲劳裂纹扩展的影响

由前述可知，损伤模型中考虑蠕变3 个阶段对模拟结果的真实性和准确性有重要影响，故在接下来的蠕变-疲劳交互裂纹扩展模拟中将使用考虑所有蠕变阶段的式(6)进行计算.

为了研究载荷大小对裂纹扩展产生的影响，对CT 试样施加保载时间为60 s，载荷比为0.05，载荷大小分别为5 kN、6 kN、7 kN 的3 种载荷，模拟结果da/dN 与ΔK 关系、da/dt 与Ct,avg关系如图10 所示.由图10(a)可知，随着载荷的增大，蠕变-疲劳裂纹扩展速度也增快，同时，随着裂纹长度的增加，裂纹扩展速度也随之增加，图10(b)也表现出相同的特征.这是由于载荷以及裂纹长度的增加使得作为驱动力的等效应力也增大，导致裂纹扩展速度加快.3 种不同载荷大小模拟结果在裂纹稳定扩展阶段，循环相关和时间相关的裂纹扩展速率与断裂力学参数的关系在双对数坐标图中分别有大致相等的斜率，并且近似处于一条直线上，出现重叠现象，且随裂纹生长长度的增加，重叠现象更加明显.尤其是da/dt 与Ct,avg关系图中的斜率重叠现象更加明显，拟合该图中各结果在裂纹稳定扩展阶段的结果曲线，得到在双对数坐标下的一元一次方程，方程的斜率按载荷由小到大依次为0.53、0.56 和0.56，3 个斜率大小非常接近，这说明其他条件固定时，这3 种载荷大小的裂纹扩展机理模式是类似的.同时也说明，不同载荷大小的Parispower 公式各系数值近似，可以通用，这简化了多余的拟合步骤，有利于实际工程应用.

图10 蠕变-疲劳裂纹扩展速率模拟结果Fig.10 Simulation results of creep-fatigue crack propagation rate

为了进一步分析，将蠕变、疲劳和蠕变-疲劳交互损伤量化，结果如图11 所示.交互损伤的计算式为

图11 3种载荷的蠕变、疲劳和蠕变-疲劳交互损伤Fig.11 Creep，fatigue，and creep-fatigue interaction damage for three load sizes

式中ωint为蠕变-疲劳交互损伤.3 种载荷情况的裂纹模拟结果中，蠕变损伤占总损伤的主要部分(大于50%)，其次是交互损伤(小于30%)，疲劳损伤最少(小于20%).随着施加载荷的增大，裂纹生长长度达到6.5 mm 时，蠕变损伤从66%增长到78%，疲劳损伤和交互损伤减小，分别从10%减少到4%、从23%减少到17%.这表明在其他条件不变的前提下，载荷增大将促进蠕变损伤，而疲劳损伤和交互损伤将减小.随着裂纹的增长，蠕变损伤增加，疲劳损伤和交互损伤减小，Liu 等[11]解释了这种现象，即随着裂纹扩展，材料的韧性连接减少，且等效应力随裂纹扩展长度的增加而增大，故蠕变损伤增加.同时，也可以观察到，裂纹进入稳定扩展阶段后，载荷越大，随裂纹生长长度增加，蠕变损伤增大得越早，疲劳和交互损伤也减小得越早，这可能是由于越大的载荷提供的等效应力越大，韧性连接减少得越快.裂纹扩展到3 mm 之后，所有载荷情况的同一种损伤的变化趋势斜率和范围近似，蠕变损伤的变化范围均为15%左右，按载荷大小由低到高，疲劳损伤变化分别为8%、9%和6%，交互损伤的变化分别为7%、8%和10%，差距同样很小，这也许是图10 两种裂纹扩展速率图中不同载荷大小结果近似处于一条直线上的原因.

3.4 载荷比对蠕变-疲劳裂纹扩展的影响

载荷比的大小反映了疲劳加载的剧烈程度，载荷比越大，载荷波中载荷的最大和最小值相差越小，改变载荷比对蠕变-疲劳裂纹扩展中各损伤变化有重要影响.有限元分析中采用了4 种载荷比，分别为0.01、0.05、0.20 和0.50，保载时间为60 s，不同载荷比的最大载荷设置均为相同的值8 kN，最小载荷分别为80 N、400 N、1 600 N、4 000 N，计算结果如图12所示.图12(a)为da/dN-ΔK 图，4 条曲线的横纵坐标大小各不相同，为了更直观地对比4 种载荷比结果，以Kmax为横坐标，绘制了da/dN-Kmax图，如图12(b)所示，由于4 种载荷比的最大载荷相同，故4 条曲线的横坐标相同，可以看出，载荷比越大，裂纹扩展速率越慢.这可能是由于增大载荷比，加载和卸载过程产生的疲劳减小，使得单次循环引起的损伤累积值减小、裂纹扩展速率减慢.同时可以观察到图12(b)中各结果曲线的斜率随Kmax的增大而增大，而图12(c)的da/dt-Ct,avg图中各结果基本为一条直线，拟合该图中各结果的Paris-power 曲线斜率，按载荷比从小到大的顺序分别为0.61、0.61、0.62 和0.64，斜率随载荷比的增大基本保持不变，这可能是由于载荷比的改变虽然会影响疲劳损伤累积，但因为每周期加载中产生疲劳的加载和卸载段时长仅占总时长的1/60，蠕变损伤仍为主导损伤，故其对总损伤造成的时间相关的裂纹扩展速率斜率的影响较小.拟合的一元一次方程截距，随载荷比增大分别为-1.49、-1.48、-1.44 和-1.18，虽然在载荷比为0.01～0.20 时的曲线非常接近，但当载荷比增大至0.50 时，其截距明显增大，同时da/dN-Kmax图中4 条曲线的截距也各不相同，故与改变载荷大小的模拟结果不同，不同载荷比的4 条曲线在两个双对数坐标轴上的截距随载荷比增大而改变，不能用相同系数的Paris-power 公式表示.

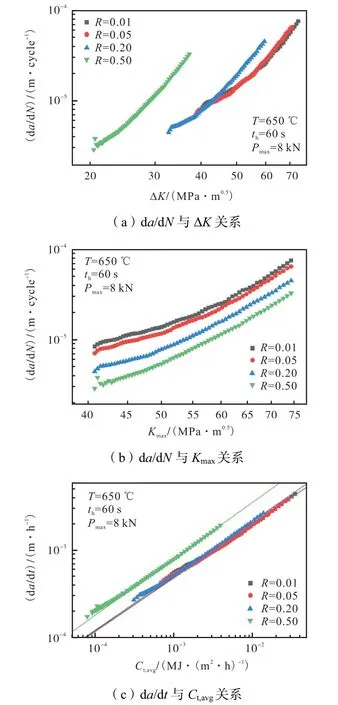
图12 载荷比为0.01、0.05、0.20、0.50 下蠕变-疲劳裂纹扩展速率模拟结果Fig.12 Simulation results of creep-fatigue crack propagation rate for load ratios of 0.01，0.05，0.20，and 0.50

对4 种载荷比结果的损伤进行了分析，如图13所示.随载荷比的增加，蠕变损伤增大，疲劳损伤和交互损伤均减小，这验证了增大的载荷比削弱了疲劳损伤，同时也削弱了交互损伤，增强了蠕变损伤，并且可以看到4 种结果的蠕变损伤占主要部分，其次为交互损伤，疲劳损伤最小，说明蠕变损伤占主导作用.载荷比为0.01 和0.05 的各损伤大小和斜率较为接近，验证了图 12(b)中两者的结果曲线非常接近.载荷比从0.05 增加到0.20 和从0.01 增加到0.05，在裂纹生长长度为3 mm 时，蠕变损伤分别增大了18%和6%，疲劳损伤分别减少了6%和3%，交互损伤分别减少了13%和3%.各损伤的变化，前者远大于后者，验证了图12(b)中载荷比为0.20 和0.05的距离相比0.01 和0.05 的更远.载荷比从0.20 增加到0.50 的各损伤中，蠕变和交互损伤变化较大，疲劳损伤都较小且变化较小，如在裂纹生长长度达到3 mm 时，蠕变损伤增加了9%，交互损伤减小了8%，而疲劳损伤仅减小了0.8%，故可知造成载荷比为0.50 的裂纹扩展速率减小的原因主要是蠕变和交互损伤的变化，这说明改变载荷比不是仅对疲劳损伤产生影响，对蠕变和交互损伤也有直接影响.当载荷比为0.50 时，其损伤基本为蠕变损伤，疲劳和交互损伤接近为0，故载荷比大于等于0.50 的蠕变-疲劳裂纹扩展过程可近似视为蠕变裂纹扩展过程，故产生疲劳损伤前提是载荷比至少要小于0.50.

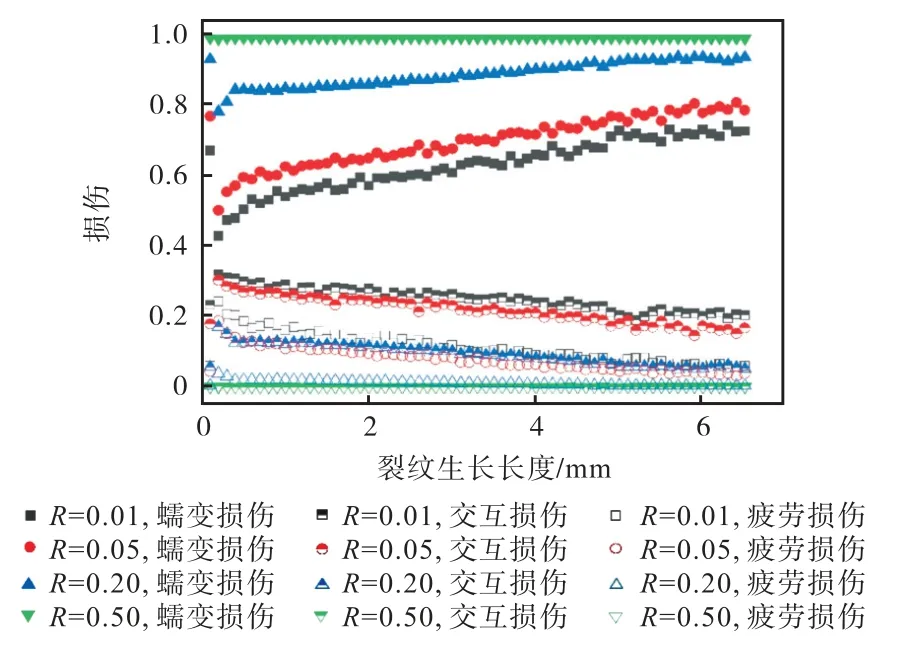
图13 4种载荷比的蠕变、疲劳和蠕变-疲劳交互损伤Fig.13 Creep，fatigue，and creep-fatigue interaction damage for four load ratios

3.5 保载时间对蠕变-疲劳裂纹扩展的影响

裂纹扩展过程中，加载波中的保载时间内产生了蠕变损伤，故保载时间长短对裂纹扩展速率和各损伤占比有重要影响.本节共设置了8 个不同的保载时间，分别为1 s、5 s、10 s、30 s、60 s、120 s、600 s 和1 800 s，其他条件不变，固定最大载荷为8 kN，载荷比为0.05，模拟结果如图14 所示.由图14(a)可见，裂纹扩展速率随保载时间的增长而增大，同时，不同保载时间试样的有限元计算结果的da/dN-ΔK 图中曲线斜率近似.相同的ΔK 下，保载时间为1 800 s 的试样裂纹扩展速率da/dN 是60 s 结果的15 倍左右，是1 s 结果的40 倍以上，但由于保载时间的不同，每个周期的时长也不同，周期越长，每周期产生的损伤越大，裂纹扩展长度也越长，故da/dN 不能准确地反映改变保载时间导致的裂纹扩展速率变化.图14(b)为da/dt-Ct,avg曲线，由图可知，保载时间越长，裂纹扩展速率越慢，8 条曲线拟合得到的斜率大小，按保载时间从小到大分别为0.54、0.56、0.59、0.61、0.61、0.61、0.62 和0.62.斜率随保载时间的增长而增大，但当保载时间大于等于30 s 后，斜率仅由0.61 缓慢增大到0.62，相比保载时间由1 s 增长到30 s 的斜率由0.54增大到0.61，变化微弱，且相同Ct,avg值下的裂纹扩展速率变化越来越小，曲线重合度越来越高，这与Tang等[12]得到的G115 模拟结果类似，说明随保载时间的增大，蠕变损伤占比增大，且保载时间超过30 s 后，蠕变损伤为主导损伤，曲线斜率近似相等，这是由于保载时间较长时，在1 个周期内，产生蠕变损伤的保载时间相比产生疲劳损伤的1 s 波形段要大得多，因此裂纹扩展的蠕变损伤占总损伤的主要部分，增加保载时长对结果曲线的影响有限.

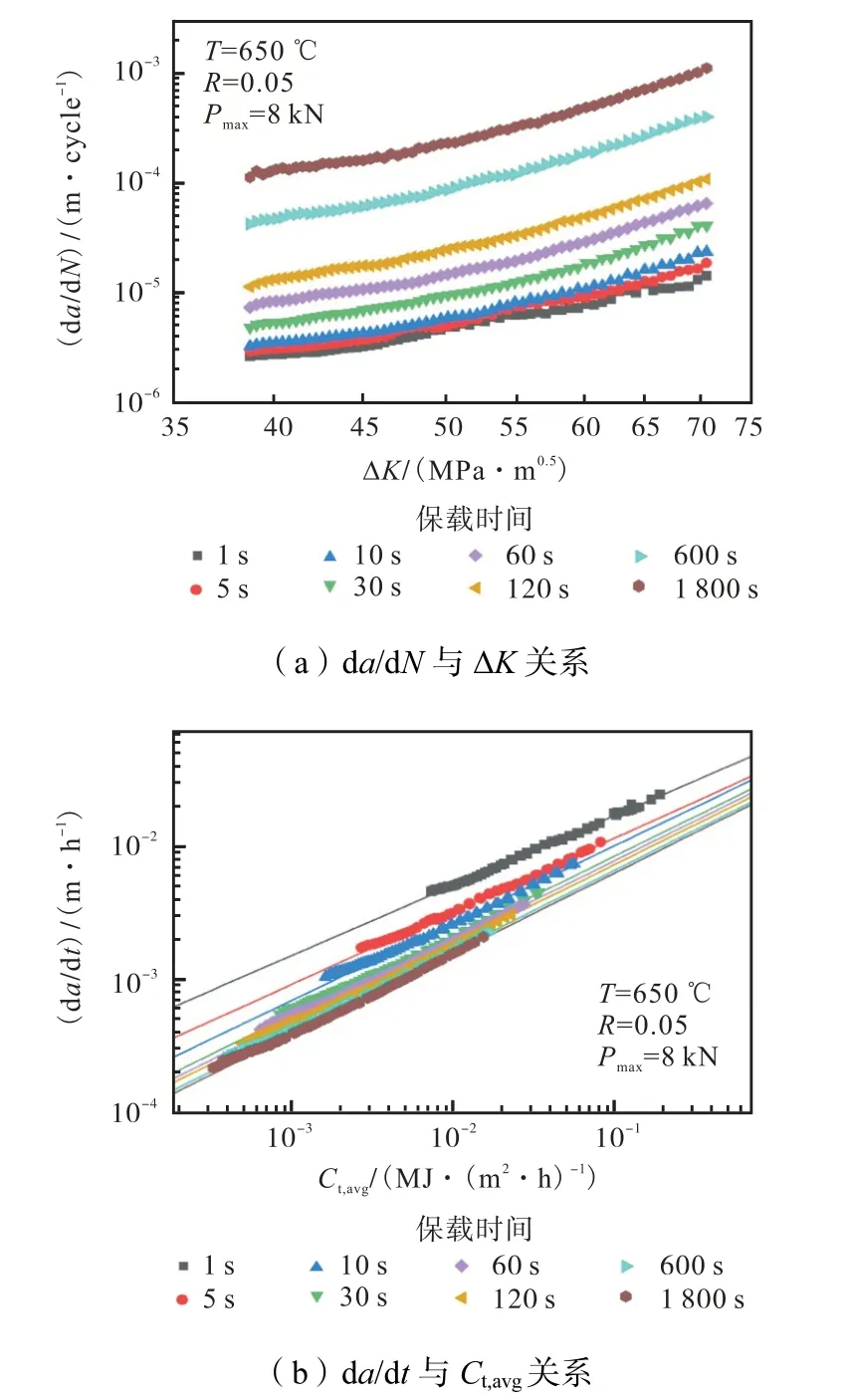
图14 保载时间为1 s、5 s、10 s、30 s、60 s、120 s、600 s 和1 800 s下蠕变-疲劳裂纹扩展速率模拟结果Fig.14 Simulation results of creep-fatigue crack propagation rate for hold times of 1，5，10，30，60，120，600，and 1 800 s

图15 展示了不同保载时间结果的各损伤变化趋势，随保载时间的增加，蠕变损伤越来越大，从4%增加到99%；疲劳损伤越来越小，从93%减小到近似为0；交互损伤在保载时间由1 s 增长到10 s 过程中，为增大趋势，保载时间为10 s 时达到峰值，保载时间继续增长，则呈减小趋势，总体大小范围为0～33%，故可知蠕变-疲劳交互载荷作用下裂纹扩展的交互损伤的上限33%远小于另两种损伤的上限99%.随裂纹生长长度增加，蠕变损伤增大，疲劳损伤减小，交互损伤在保载时间小于10 s 时，趋势不明显，保载时间大于等于30 s 时，为减小趋势.由于各损伤随裂纹生长长度的增长会有一定变化，为方便进行整体比较，求得了各保载时间结果的各损伤的平均值，如图16所示.平均值y计算式为

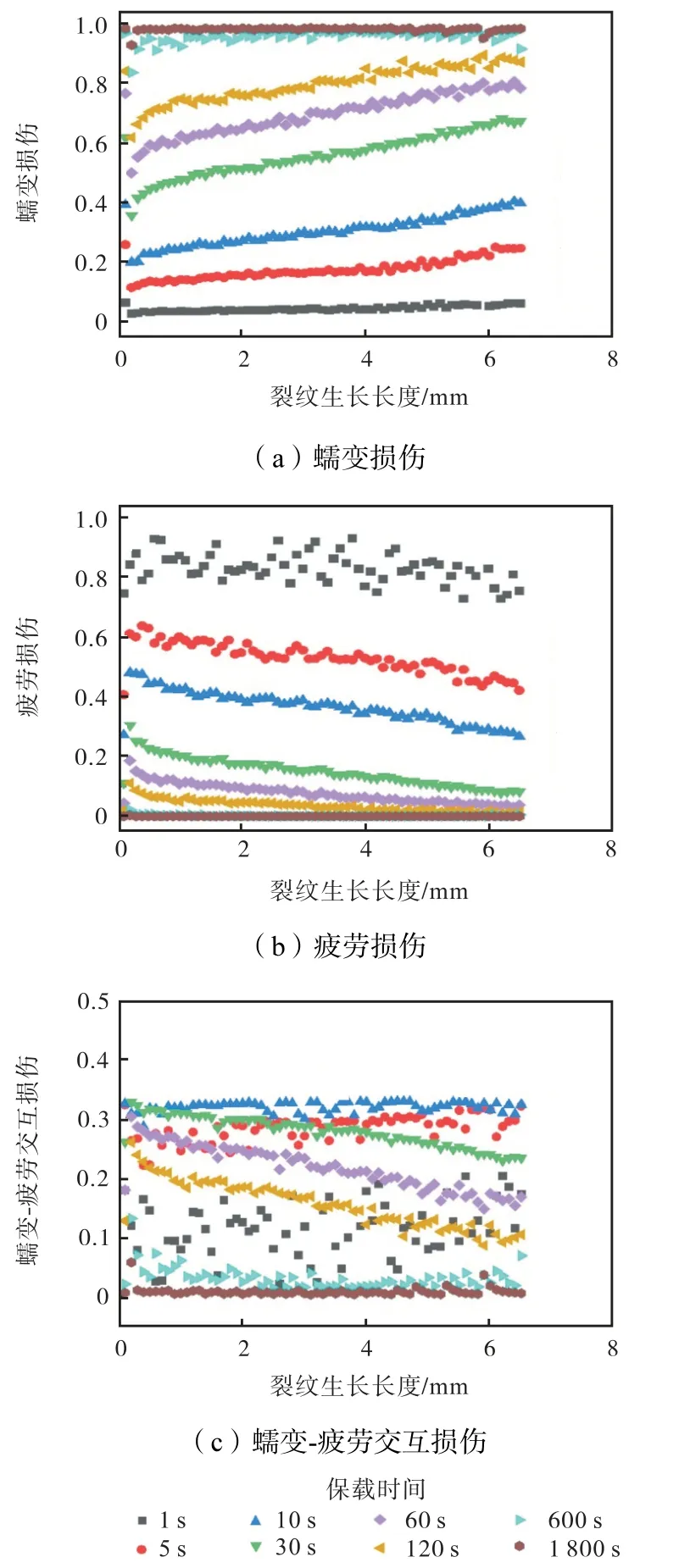
图15 8种保载时间的蠕变、疲劳和蠕变-疲劳交互损伤Fig.15 Creep，fatigue，and creep-fatigue interaction damage for eight hold times

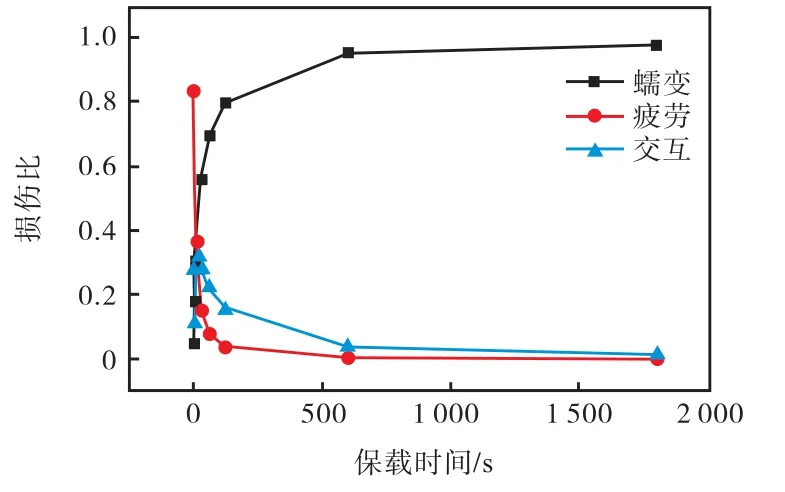
图16 8 种保载时间的平均蠕变、疲劳和蠕变-疲劳交互损伤Fig.16 Average creep，fatigue，and creep-fatigue interaction damage for eight hold times

式中：m 为所取裂纹生长长度数值；Δaj为第j 个裂纹生长长度；ωy为蠕变损伤ωc或疲劳损伤ωf或交互损伤ωint.保载时间大于等于30 s 时，蠕变损伤将超过50%，成为主导损伤，这验证了上述图14(b)中保载时间大于等于30 s 的结果曲线斜率变化小且大小变化较小的表现.保载时间小于等于5 s 时，疲劳损伤大于50%，为主导损伤.保载时间为10 s 时，疲劳损伤为37%，与31%的蠕变损伤和32%的交互损伤相近，证明了疲劳和蠕变控制模式的分界点为10 s[14]的结论，且此时的交互损伤达到了最大值.由于保载时间为600 s 的平均蠕变损伤为96%，接近100%，故保载时间大于600 s 时，裂纹扩展过程中的损伤基本为蠕变损伤，接近纯蠕变裂纹扩展.保载时间为1 s 时疲劳损伤为83%，故保载时间小于1 s 的裂纹扩展，也近似接近纯疲劳情况.

4 结 论

本文推导了考虑蠕变3 阶段的蠕变本构模型，通过损伤力学与有限元相结合方法对650 ℃蠕变-疲劳载荷作用下哈氏合金X 的CT 试样裂纹扩展过程进行了数值计算，获得的主要结论如下.

(1) 结合应变硬化定律与连续损伤力学模型得到考虑蠕变所有阶段的本构模型，对比考虑不同蠕变阶段的纯蠕变裂纹扩展模拟结果，得到考虑所有阶段的本构模型结果准确性更高.载荷越大，考虑蠕变第Ⅱ和第Ⅲ阶段的预测差异越小，考虑蠕变第Ⅰ阶段的预测差异越大.

(2) 随着载荷幅值增大，蠕变-疲劳裂纹扩展速率增大，载荷幅值从5 kN 增加到7 kN，蠕变损伤均为主导损伤，交互损伤次之，疲劳损伤贡献最低，且随裂纹扩展长度和载荷的增大，蠕变损伤对损伤累积贡献上升.

(3) 随着载荷比的增大，蠕变-疲劳裂纹扩展速率减小.在8 kN 载荷、保载时间为60 s 的条件下，载荷比从0.01 至0.50 的4 种模拟结果中蠕变损伤均为主导损伤，随载荷比的增大，蠕变损伤增加，交互损伤和疲劳损伤减少，载荷比为0.50 时近似为纯蠕变裂纹扩展.

(4) 随着保载时间增大，裂纹扩展速率da/dN 增大，而da/dt 减小，da/dt-Ct,avg曲线斜率增大，蠕变损伤增大，疲劳损伤减小，交互损伤先增大后减小.蠕变和疲劳损伤主导的分界保载时间为10 s，且此时交互损伤达到峰值.保载时间大于600 s 和小于1 s 时可分别近似视为纯蠕变和纯疲劳裂纹扩展.