输入量化下航天器位姿一体化预设时间控制

2024-01-20张洪珠叶东孙兆伟

航空学报 2023年22期

张洪珠，叶东，孙兆伟

哈尔滨工业大学卫星技术研究所，哈尔滨 150001

近年，轨道快车、“棱镜”双星（Prototype Research Instruments and Space Mission Technology Advancement，PRISMA）和蜂鸟一号（HummerSat-1）等空间任务取得了巨大成功。为保障任务航天器“健康”以长期遂行目标任务，在轨对其进行故障抢修和常规维护是必要的。实施救援和维护过程中，往往要求主动航天器（维护航天器）必须能够以期望的状态快速准确地到达维护接口，并相对目标航天器（故障航天器）保持悬停和姿态同步从而顺利实施维护操作［1］。因此，航天器姿态轨道快速高精度控制问题成为航天工程领域研究的热点［2］。

有限时间控制由于可突破收敛的渐近性，同时具有更好的控制性能和出色的鲁棒性，因而广泛应用于航天器姿态控制领域［3-4］，如基于终端滑模方法［5-6］、加幂积分技术［7］和齐次性理论［8］等设计的有代表性的有限时间控制方案。值得注意的是，有限时间控制策略状态收敛时间的估计依赖于系统的初始状态，但对于某些空间任务而言，航天器的初始状态难以预先准确获知［2］，从而将导致系统收敛时间难以确定和分析［9］。因此有限时间控制在实际应用中受到较大限制。为解决有限时间方法对系统初值的依赖问题，学者们提出了固定时间控制方法［10］。该方法不仅能够使得被控系统在有限时间内获得良好的动态性能，而且系统的收敛时间也不受初始状态的影响。作为有限时间概念的改进，固定时间方法在航天器控制领域也与滑模控制、幂积分、极限齐次等技术结合，取得了丰硕的研究成果［11-15］。但是，面向实际应用，该方法仍显不足。工程上，系统收敛时间和收敛精度等指标一般根据任务的工程目标首先确定，然后在指标范围内设计满足要求的控制算法。如：对于推力矢量航天器，在维护机动过程中，航天器姿态需在指定时间内以足够的精度匹配特定方向，进而，推力器可在期望方向上施加脉冲推力，以在指定时间内跟踪目标航天器的位置和速度，完成交会［16］。然而，如文献［17-18］指出，固定时间技术的系统收敛时间与控制参数之间关系复杂，不能直接表示为系统的某个可调参数。因此限定系统收敛时间的条件下，该方法不易选择控制参数，不利于实际应用［19］。为解决固定时间方法的局限性，预设时间稳定概念受到关注［20］，其收敛时间去除了对系统初值的依赖、且仅由一个特定的控制参数显式决定。该概念良好的理论性质获得了学者们的青睐［21-24］。文献［21］针对一类“欧拉-拉格朗日”型非线性系统，提出了一种新颖的实际预设时间控制方法。该方法引入坐标变换思想，使得存在和不存在状态约束时，误差变量皆可在预设时间内收敛到指定区间，且对系统不确定性具有良好的鲁棒性。然而，该方法巧妙的处理思路使得设计过程变得复杂。文献［22-24］采用了不同的设计思路，通过控制器设计使得系统李雅普诺夫函数的变化率满足特定的预设时间收敛形式，解决了不确定性估计和航天器控制问题。然而，上述研究仅面向航天器姿态控制问题，而未考虑航天器的轨道控制问题。

在轨维护等空间近距任务的航天器控制中，既需进行姿态控制也需进行轨道控制，且二者相互耦合。传统上，一般对姿态和轨道运动进行分别建模、独立控制，控制实施时，也常采用姿轨交替的控制方式。但是，此种模式往往因忽略姿轨耦合效应而降低模型精度，尽管控制器中加入修正项可在一定程度上补偿耦合影响，但可能仍无法满足高精度的任务要求［25］；此外，位姿分控方式，一方面难以实现姿态轨道同时到达期望状态的控制目标，同时也将导致整体机动时间变长，致使快速位姿机动受到掣肘。可见，航天器姿轨耦合快速机动控制问题研究具有重要意义。

预设时间概念解决具有收敛时间约束的非线性控制问题优势显著，但是，该方法用于解决带有时间约束的姿轨耦合控制问题，尚较鲜见。航天器控制领域，为解决独立建模方式存在的不足、提高控制性能，李群SE（3）框架下的航天器运动描述成为姿轨耦合建模的主要方式之一。本质上，空间近距离姿轨耦合控制问题可抽象为空间六自由度相对运动控制问题，SE（3）指数坐标下六自由度相对运动描述能够融合位姿耦合特性［5］，具有一些良好性质，是位姿一体化控制研究的热点。然而，指数坐标下，系统运动学和动力学皆是耦合的，其非线性更强，动态更复杂。基于预设时间方法［21-22］进行位姿跟踪控制，首先限定了其收敛时间，而收敛时间的约束也将对系统其他性能产生较大影响。因而，指数坐标下，其复杂的系统动态，将使得预设时间控制器的设计更具挑战。

对于执行维护操作的微小型航天器，平台配备的通信设备的功率和信道带宽有限，而其控制与执行机构分系统之间又通常采用无线方式，因此，微小型航天器系统的通信能力受到较大限制［26］。考虑这一问题，微小航天器的控制系统设计需满足快速机动目标，还需考虑其通信能力受限问题。目前，处理通信约束问题的主要思想包括量化控制和事件驱动控制。相比于后者，前者在降低系统通信频率的同时，也能够减小单次通信中传输信号的数据量，是航天器控制策略研究的一个重要方面。输入量化是量化技术的具体实现。该技术将连续信号变换为分段恒定输入信号，并在恒定时段内暂停通信从而降低控制器和执行机构间的通信频率。然而，在位姿一体化系统下考虑量化控制，由于输入力和力矩对系统状态轨迹的影响是耦合的，且二者往往具有量级差异，因此，如果粗略地对输入信号进行量化将产生较大输入偏差，可能导致系统性能的严重下降，抑或无法满足实时性较高的任务要求，甚至可能导致系统不稳定［27］。综上所述，考虑输入量化问题的快速位姿一体化控制具有显著的必要性和工程意义［28-29］，也更为复杂。

面向小型航天器执行在轨维护任务中具有时间约束的高精度位姿控制问题，本文利用李群SE（3）框架描述融合姿轨耦合效应的航天器六自由度空间运动，采用新型的误差有界量化器对系统输入进行量化，并引入偏差补偿策略，接引量化参数抑制其对控制性能的不利影响，进而在预设时间稳定概念下设计一体化位姿跟踪控制算法。主要工作和贡献如下：

1）运用李群SE（3）上指数坐标表示的航天器姿轨耦合误差动力学模型，在惯性参数未知、外部干扰以及力和力矩信号量化的条件下，解决了具有时间约束的快速位姿跟踪控制问题。

2）引入误差有界复合量化器减小控制器到执行机构的通信量，保证系统稳定性的前提下，有效降低了系统通信负载；并利用量化参数设计偏差补偿结构，对量化误差进行对应通道补偿。

3）推导了实际预设时间稳定引理，并基于反步法设计位姿一体化非奇异控制算法。该算法在扰动信息未知和不依赖系统初始状态的情况下，实现了指定时间内高精度位姿跟踪，且系统的稳定时间上界可由一个控制增益预先设定。

1 姿轨一体化模型及问题描述

群是由集合及定义在集合上的二元运算组成的代数结构，李群是一类具有光滑性质的群结构，特殊欧几里德群SE(3)是一类特殊的李群，它可以表示刚体的一般空间构型。刚性航天器作为一种特殊的刚体，其空间运动可以由SE(3)的齐次坐标及相应的李代数se(3)描述［30-31］。

1.1 刚体航天器运动模型

惯性空间中，航天器的位置和姿态构型可由SE(3)上的元素表示，即

式中：C∈SO(3)为航天器从本体坐标系到惯性坐标系的方向余弦矩阵；R=[R1R2R3]Τ∈R3为惯性系下航天器质心的位置矢量，其原点位于地心。

为一体化描述航天器运动，定义航天器广义速度为

式中：ω和υ分别为本体坐标系下航天器的角速度和平移速度。

SE（3）上航天器运动学方程可以一体化地表示为［31］

根据文献［31］，航天器姿轨耦合一体化动力学方程可表示为

式中：Ξ=diag(J，mI3)∈R6×6为航天器惯性参数矩阵，其中J和m分别为航天器的转动惯量和质量，Ij为j阶单位阵，j为正整数；=(ℵv)T为广义速度的反伴随矩阵，其中，ℵv为广义速度的伴随矩阵，定义为为地球引力相关输入向量，Mg=，分别为作用在航天器上的重力梯度力矩、重力和J2摄动力，这里Rb=CTR为航天器质心位置向量在本体系下的表示，μ=3.986×1014m3/s2、J2=1.082 63×10-3和R⊕=6 378 km 分别代表地球引力常数、地球扁率摄动和地球平均半径为控制输入向量，其中Mc和Fc分别为输入力矩和输入力；为作用在航天器上的环境干扰向量，其中Md和Fd分别为干扰力矩和干扰力。

1.2 航天器姿轨一体化相对运动模型

考虑一个由目标航天器和主动航天器构成的两航天器系统。假定两航天器（其中目标既可以是真实航天器也可为虚拟的）的空间构型分别为go和g，则该系统的相对位姿构型可表示为。设主动航天器的期望位姿构型表示为gd，该期望构型一般可通过目标航天器构型通过gd=goχd给定，其中χd为根据空间任务指定的系统的期望相对位姿构型，通常为一个常量。

基于上述定义，主动航天器相对于目标航天器的位姿构型跟踪误差为。进而可得误差运动学为

为简化控制器设计，引入李代数的指数坐标表示位姿跟踪误差［30］。记，其中Ce为姿态跟踪误差方向余弦矩阵，Re为位置跟踪误差。定义η=[θTβT]T∈R6表示位姿跟踪误差的指数坐标，其中θ和β分别为指数坐标下的姿态跟踪误差和位置跟踪误差。指数坐标可由李群和李代数间的对数映射得到，即

式中：(·)∨为(·)∧的逆变换。

通过课外实验，让学生在自主创造和自己动手中体会学习物理知识的乐趣，并在学习中加深对知识的理解。在教材中，很多生活化的实验都可以让学生借助生活材料学习，并在课下自主探索。

logSE(3)(χe)的计算结果为

其中：tr(·)为矩阵(·)的迹。

于是，得到指数坐标形式的误差运动学方程为［31］

式中：G(η)为分块三角矩阵，定义为

不失一般性地，假定两航天器系统的期望相对速度为零。对广义速度跟踪误差ve求导，得到两航天器位姿跟踪误差的相对动力学方程为［31］

考虑实际任务中航天器惯性参数并非精确可知，因此，设航天器惯性参数矩阵及其逆分别表示为，其中，Ξ0为惯性参数矩阵的标称部分，ΔΞ为不确定部分，为惯性参数矩阵逆的不确定部分。进而，位姿跟踪误差动力学方程式（10）可表示为

1.3 输入量化

假定u=[u1，u2，…，u6]∈R6为待量化的控制力矩和力，uc=Q(u)=[Q1(u1)，Q2(u2)，…，Q6(u6)]为u的量化值，Qi(·)为基于对数量化算法和均匀量化算法的复合量化器。根据文献［27，32］，该量化器可定义为

对数量化器定义为

式中：ui，j=(ρi)1-jui，min；δi=(1 -ρi)(1 +ρi)(j=1，2，…，n)，其中n为正整数，0 ＜ρi＜1 表征对数量化器的量化密度；ui，min＞0 为待设计量化死区。当控制输入幅值大于阈值时，量化器切换为式（14）定义的非对称均匀量化器：

至此，定义复合量化器的量化误差为

根据对数量化器和均匀量化器的性质，可得复合量化器的量化误差有界，且满足：

基于式（15）的定义，量化后的系统输入可表示为uc=Q(u)=u+Δq，其中Δq为六通道量化误差。

2 预设时间位姿一体化控制器设计

本节首先给出本文的控制目标和常用假设及相关引理；接着推导满足一般条件的实际预设时间稳定引理；最后，利用该结果设计输入量化条件下的位姿一体控制策略。

2.1 控制目标

基于第1 节的定义，本文的控制目标可描述为：对于考虑输入量化的航天器相对运动误差系统式（8）和式（11），设计一个非奇异的一体化控制律，使得位姿跟踪误差在任意初始条件下，皆可在预设时间内收敛到原点的有界邻域。即对于η(0)∈R6，当t＞T时，η(t)∈L∞成立。

2.2 假设及引理

假设1目标航天器的广义速度和广义加速度有界，即为正常数。

假设2［30，33］主动航天器受到的环境输入干扰和总干扰有界，即，dd和d为未知正常数。

引理1［23］对于任意xj＞0 (j=1，2，…，n)，下面的不等式成立：

引理2［34］对于x，y∈R 和常数τ1＞0，τ2＞0，q＞0，下面的不等式成立：

引理3［34］对于实数x，y，w∈R，满足x≥y和w＞1，则下面的不等式成立：

引理4对于系统=f(x，t，d)，其中，x∈Rn，d∈Rn分别为系统状态和外部扰动，如果存在一个连续正定函数L(x)，对于系统任意解x(t，x0)和标量参数0 ＜p＜1、预定义时间常数使得式（17）成立：

则系统的解轨迹是实际预设时间稳定的，L在时间[ T ]内到达包含平衡点的区域内，其中min{·}表示集合{·}的最小元素，表示系统的收敛时间，满足≤T。

证明受文献［35］证明思路启发，式（17）可以表示为

将式（19）代入式（20）得到：

进一步变形，式（21）可表示为

注释1对于系统=f(x，d，t)，文献［36］在干扰有界且部分信息可知的条件下给出了预设时间稳定定理稳定时间上界为T。文献［23］则在干扰有界但信息未知的条件下，给出了实际预设时间稳定定理，并在特定情形下给出系统的预设收敛时间为。注意到，当L＞1 时，在L收敛中起主要作用，当L＜1 时，在L收敛中起主要作用。本文引理4 在文献［23］定理的基础上进一步引入了可调参数ℓ，即，该形式改变了文献［23］中高低幂次项前的最小系数，增加了低幂次项前的权重，减小了高幂次项前的权重。系统存在有界扰动时，该引理可实现系统状态在预设时间T内收敛。相比文献［23］，引理4 在一般的情形下，得到系统收敛时间的估计更小；此外，在系统初始状态远离平衡点时，能够降低系统状态的最小下降速度。因此，引理4 给出系统收敛时间的估计更具一般性；此外，该引理用于控制器设计时，有助于减小系统状态较大时的控制输入。对于位姿一体化误差系统，其相对位置误差可以很大，因此，基于该引理设计位姿控制器有利于降低系统的最大控制力，具有一定实际意义。

2.3 反步控制器设计

为满足后文应用，首先给出关于矩阵G(η)的性质。

命题1对于状态空间中的任意状态向量η∈R6，式（9）定义的矩阵G(η)是可逆的。

证明由式（9）的表达式可知，G(η)为状态相关的时变分块下三角矩阵。证明采用反证法、分为两种情况进行。

情况1η≠0

如果A(θ)存在0 特征值，则存在非零向量∈R3使得，A(θ)=0，因而有：

根据A(θ)的定义，可得

考虑到θ×θ×=-θTθ·I3+θθT，式（26）可表示

再由θ=‖θ‖，可得A(θ)＞0，此结果与式（25）矛盾。因此，0 不是A(θ)的特征值。

情况2η=0

由G(η)的定义，利用洛必达法则容易验证：

综上所述，G(η)为特征值非零的下三角分块矩阵。因此，对于任意η∈R6，矩阵G(η)可逆。命题1 证明完毕。

观察式（8）和式（11），该系统为典型的二阶级联系统，基于系统特征和性质，采用反步法［37］设计位姿一体化控制器。

步骤1虚拟控制律设计

定义中间误差变量z1=[z11，z12，…，z16]=η和，其中，为待设计的虚拟控制律，K1=diag(k11，k12，…，k16)为正定对角矩阵。易得中间变量z1的微分方程为

设计虚拟控制律为

当|z1i|＞ε1i，式（31）代入式（30）中，推导得到：

应用引理1 和杨氏不等式，式（32）可放大为

式中：λK2为矩阵K2的最小特征值；k为任意正常数；Λm=min{Λ1，Λ2，…，Λ6}，其中，Λm按引理4参数ℓ 的条件取值。选取式（34）：

式（33）可简化为

步骤2实际控制律设计

首先对中间变量z2求导，得到：

由式（31）和式（37）易知，虚拟控制律ωˉ及其导数皆是非奇异的。

注释2对系统式（8）和式（11），采用反步法设计控制器时，中间误差变量一般可设计为z2=ve-。本文设计的中间变量与之不同，其中包含了矩阵G(z1)，这将使得系统在动态响应阶段，能够利用位姿跟踪误差信息调节系统动态；同时，在稳态阶段，由于G(z1)→I6，可保证虚拟控制律跟踪系统广义误差速度的反步设计初衷。

由1.3 节定义可知，量化器式（12）具有有界性质。定义ςi＞0 表示量化误差的界，即|Δqi|≤ςi。根据式（16），可知ςi=max{σi，δi|ui，s|+ui，min}，其中max{·}表示集合{·}的最大元素。于是可得

将Q(u)代入到式（36）中得到

为推导变量z2的有界性，对式（39），定义正定标量函数，以之增广Vz1得到系统李雅普诺夫函数V为V=+。对其求导并代入式（39），得到：

定义um=u-u1，考虑命题1，设计控制指令：

式中：K3=diag(k31，k32，…，k36)为正定对角阵。

将u1代入式（40）得到：

式（42）中，量化误差和不确定性是设计控制指令um需进一步考虑的问题。为处理输入量化误差对系统稳定性带来的不利影响，在控制器中，采用补偿策略，引入量化器参数信息抑制量化误差。定义u3=um-u2，设计误差补偿结构为

注释3本文考虑到位姿控制力和力矩一般为不同量级的实际，对力和力矩通道实施不同水平量化，并基于复合量化器误差有界性，利用量化参数设计误差补偿项，降低系统通信负载的同时保证系统的稳定性。

对于系统式（39），系统不确定性也将影响控制性能，为处理该消极影响，设计如下更新律对系统干扰进行自适应估计

设计控制指令

注释4文献［39］在假定环境干扰有界且界已知的条件下，给出了预设时间和指定收敛范围的姿态跟踪控制器。然而，当考虑系统总扰动时，由于其界难以预先获得，因此其方法存在一定的局限性。针对此问题，本文设计了扰动自适应律式（44）估计扰动上界的平方，其第一项可提高系统鲁棒性的同时减轻抖振现象，后两项则使得整体系统具有预设时间收敛的性质。

基于步骤1 和步骤2 的设计，得到考虑不确定性和输入量化的整体预设时间位姿一体跟踪控制器为

基于上述分析和设计过程，本节最后给出如下定理。

定理1考虑式（8）和式（11）构成的两航天器相对运动误差系统，在假设1 和假设2 满足并考虑输入量化的条件下，如果选择参数满足条件式（34）和式（59），虚拟控制律式（31）、实际控制律式（47）、量化补偿项式（43）和自适应律式（44）能够使得位姿跟踪误差在预设定的时间T内收敛到包含原点的小的邻域内，即主动航天器能够在任务设定时间内，以足够的精度跟踪目标航天器。

2.4 稳定性分析

为使求解过程完整，本节在Lyapunov 稳定性理论框架下，给出定理1 的证明。

证明选择式（45）得到的V为整体系统李雅普诺夫函数，对其沿闭环系统轨迹求导得到：

代入式（43）和式（44），更新式（49）为

将式（46）和式（35）代入式（50），得到V的不等式并放大可得

考虑到对于任意x∈R、q＞0，双曲正切函数有的性质，且ζ＞ς，因此式（51）可简化为

将式（54）代入到式（53），并应用二次型不等式，可得

应用上面不等式关系，式（56）可变化为

式（57）整理化简可得到式（58）：

选择参数满足式（59）所示条件：

考虑前文参数关系式（34），则根据引理1，可得系统李雅普诺夫函数导数满足式（60）：

至此，根据引理4 可知V有界，且可在预定时间T内收敛于下式所示的包含原点的区域内

进而可得，中间误差变量z1、z2和自适应误差有界，且位姿跟踪误差范数‖η‖在时间T内收敛到区域内，其中λK1为矩阵K1的最小特征值。此外，由状态的有界性可知有界，由z2的定义可知有界，由此可得广义误差速度ve有界。定理1 证明完毕。

3 数值仿真分析

本节以空间在轨维护任务为应用场景，验证本文提出的输入量化下位姿一体化预设时间控制策略的有效性及跟踪性能。

3.1 任务描述及仿真结果

假设被维护航天器为对地监测微小卫星组网系统的一颗突发故障卫星，为及时修复故障以保障组网卫星系统的对地服务能力，需要调配其他航天器（称为维护航天器）对其实施抢修和维护。因此，维护航天器需要快速到达维护位置、建立维护姿态，并且在维护过程中保持对故障航天器的运动跟踪，以便操作机构实施维护动作。两航天器运动的初始状态与文献［33］相同。目标航天器运行在高度为400 km、倾角为45°的圆轨道上，其体坐标轴与惯性主轴重合，发生故障时，初始位姿构型和速度在其本体系下分别为

故障航天器的转动惯量矩阵和质量分别为Jo=[25，0，0；0，22，0；0，0，23] kg·m2和mo=100 kg，且不考虑转动惯量和质量的不确定性。维护航天器的初始姿态按目标航天器体坐标系的zyx轴相继旋转[80.26°，30.00°，-35.26°]得到，初始位置在目标航天器体坐标系下[15，-10，-20]Tm处；角速度和平移速度在其体坐标系下分别为ω=[0.043 487，0.042 570，0.017 761]T（°）/s 和υ=[7 256.5，-1 537.1，1 712.5]Tm/s。为便于后文对比说明，记该初始位姿构型和速度为初态1。维护航天器的标称转动惯量为J=[25，1，0.5；1，22，1.2；0.5，1.2，23] kg·m2，标称质量为m=105 kg，考虑其不确定部分分别为ΔJ=0.12J和Δm=0.03m。不失一般性地，假定维护航天器的期望维护姿态与故障航天器相同，维护操作点在故障航天器体坐标系下x轴负方向5 m 位置。仿真中不考虑故障航天器受到的空间干扰，考虑维护航天器受到的干扰与文献［13］形式相同，并增大了干扰频率，设定为ud=0.005·[sin(0.2t)，cos(0.1t)，-sin(0.3t)，sin(0.2t)，cos(0.1t)，-sin(0.3t) ]T，干扰力矩量纲为N·m，干扰力量纲为N。任务设定维护航天器需在120 s内到达维护状态。考虑到执行机构输出能力是实际受限的，与文献［19，24］的处理方式相同，仿真中限定三轴控制力为[-5，5] N，三轴力矩为[-0.5，0.5] N·m。自适应参数初值(0)=0.000 1。控制及量化参数设置见表1。

表1 控制器和量化器参数Table 1 Parameters of controller and quantizer

仿真结果如图1～图6 所示。图1 和图2 分别为姿态和位置跟踪误差，图3 和图4 为角速度和速度跟踪误差。

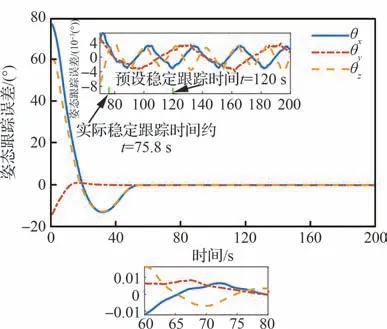
图1 姿态跟踪误差Fig.1 Tracking error of attitude

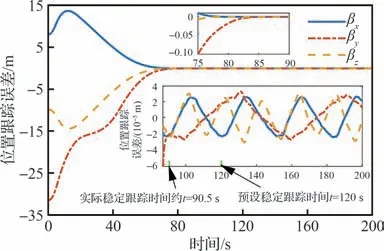
图2 位置跟踪误差Fig.2 Tracking error of position

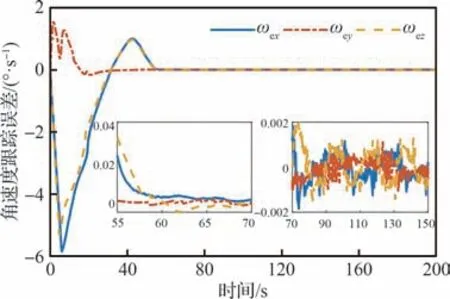
图3 角速度跟踪误差Fig.3 Tracking error of angular velocity

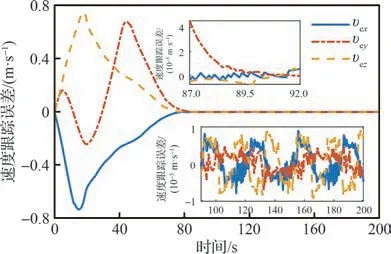
图4 速度跟踪误差Fig.4 Tracking error of translational velocity

由图1 和图2 可见，姿态误差和位置误差的收敛时间约为75.8 s 和90.5 s。进入稳定区间后，姿态误差下降到|θi|≤3.72×10-3（°）（i=x，y，z，下同），位置误差下降到|βi|≤3.28×10-5m。相应地，如图3 和图4 所示，角速度和速度误差分别在约76.2 s 和90 s 进入稳定区间，并收敛到|ωi|≤1.60×10-3（°）/s 和|υi|≤1.02×10-5m/s范围。由以上结果可知，机动中，姿态和位置误差及广义速度误差皆在120 s 内收敛，误差收敛范围在10-3～10-5量级之间。

图5 和图6 分别为量化的控制力矩和控制力曲线。可见，系统的指令输入经量化后转化为不连续的实际控制力矩和控制力，信号量化有效。需要指出的是，量化输入在ui，s之内出现了较高频率的切换，该现象是由于量化误差处于2 个量化级之间的临界切换点产生的，将对数量化器替换为迟滞量化器可降低该切换频率。

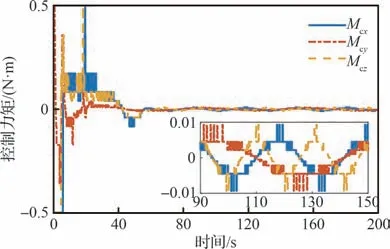
图5 量化的控制力矩Fig.5 Quantized control torque

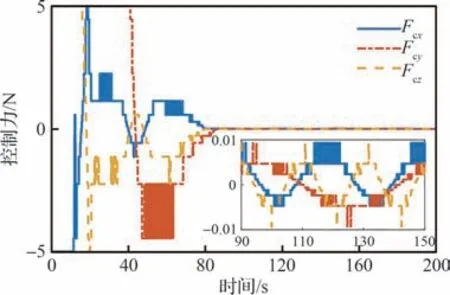
图6 量化的控制力Fig.6 Quantized control force

图7 为系统总扰动上界平方的自适应估计曲线，由图可见，估计值经过快速超调后迅速下降，并在系统状态收敛前稳定。

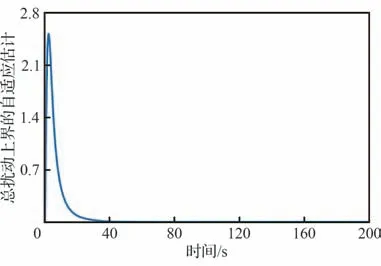
图7 总扰动上界自适应估计Fig.7 Adaptive estimation of bound of disturbance

为说明输入量化机制降低系统通信负载的能力，对量化后控制力矩和控制力信号的驻留时间进行了计算，结果分别如图8 和图9 所示。

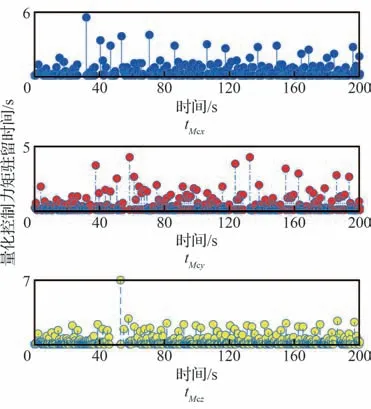
图8 量化控制器力矩的驻留时间Fig.8 Dwell time of quantized control torque

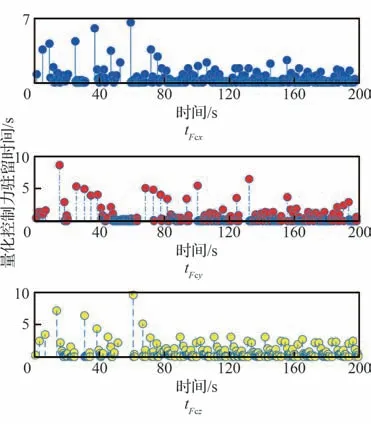
图9 量化控制器力的驻留时间Fig.9 Dwell time of quantized control force

可见，动态响应阶段，量化控制力矩的最大驻留时间接近7 s，量化控制力的最大驻留时间约为10 s；收敛到稳定区间后，驻留时间同样多大于系统控制周期。由图9 可见，在指令信号较大的动态阶段，量化明显粗略，更有利于降低通信频率。考虑控制频率为8 Hz，则六通道无量化情况下信号传输频次为9 600 次，而量化后的信号传输频次约为2 863 次，通信量可减少70%以上。结果说明，考虑控制力矩和控制力信号量化能够显著降低信号传输频次，极大减轻耦合系统的通信负担。

上述结果表明，本文给出的位姿一体化控制器是有效的，即可在输入量化的情况下，实现维护航天器在预设定时间内到达并保持在期望的维护状态，且控制精度较高，满足在轨维护任务要求。此外，采用具有误差有界的复合量化器，且力和力矩通道采用不同量化参数，能够更好的平衡减小通信量和保持系统控制性能之间的矛盾，适合位姿一体化控制。

此外，为表明本文控制算法对运行周期的要求，图10 给出了200 s 仿真中每个控制周期计算控制指令的单次时间消耗和平均时间消耗。仿真计算机为办公笔记本，处理器为Intel（R）Core（TM）i5-8250U，CPU 主频为1.60 GHz，内存8 GB，Win10 操作系统，仿真软件为MATLAB 2021a 版本。可见，计算一次指令的最大时长约为0.002 5 s，1 600 次计算的平均耗时约为0.001 1 s，均远小于控制周期。因此，该控制算法具有较高的计算效率，满足工程应用要求。

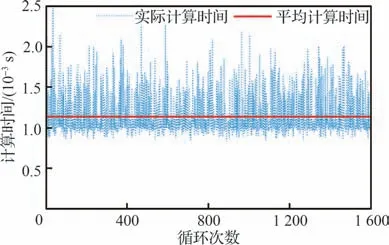
图10 控制指令计算时间Fig.10 Time cost of calculating control command

3.2 控制律性能仿真分析

1）预设时间收敛性分析

为进一步说明控制器式（47）中预设时间参数对系统稳定时间的影响，考虑了另外3 组仿真：预设时间参数T分别取值为140、100 和80 s，两航天器的初始条件和其他控制参数与3.1 节相同。3 种情况的位姿跟踪误差范数如图11 所示。

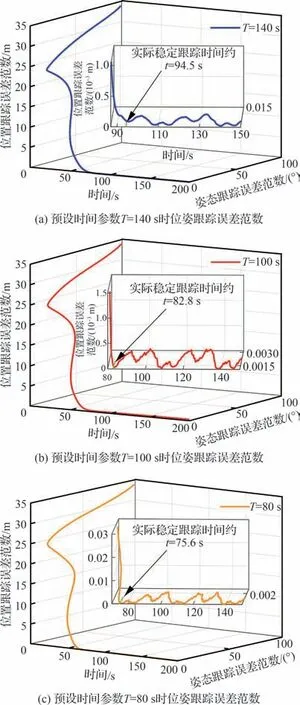
图11 预设时间参数T=140，100，80 s 时位姿跟踪误差范数Fig.11 Norm of pose tracking errors with control parameter T=140，100，80 s

由图11（a）可见，当T=140 s 时，位姿误差实际稳定跟踪时间约为94.5 s；由图11（b）可见，T=100 s 时约为82.8 s；由图11（c）可见，T=80 s时约为75.6 s。根据该结果可知，预先设定时间参数直接影响系统收敛时间，且3 组条件下，系统实际收敛时间均小于相应的预设时间参数，改变参数T可调节系统的收敛时间。上述结果验证了预设时间控制的良好性质。基于该性质，可利用预设时间参数约定系统的收敛时间上界，相对于有限时间控制和固定时间控制，预设时间方法提高系统收敛时间调节的便捷性，更有工程应用优势。此外，误差变量的实际收敛时间与设定的收敛时间具有一定的保守性，其主要原因可从两个方面考虑：一方面，理论收敛时间是在初始误差趋近于无穷的情况下给出的收敛时间上界，而系统的实际收敛时间是与系统初态和输入相关的，在确定的初态下，其实际收敛时间一般不会达到其理论上界；另一方面，控制器设计中的不等式放大也带来了系统收敛时间的保守性。考虑到，预设时间引理中的参数ℓ 与收敛速度正相关，参数p与收敛速度的相关性随状态不同而不确定。因此，可通过减小参数Λ以及精细的不等式放缩减小保守性。

2）与有限时间终端快速滑模位姿跟踪控制器［33］（下称有限时间滑模控制器/Finite Time Sliding Mode Control，FTSMC）对比分析

为说明本文设计的位姿跟踪控制器（下称反步预时控制器/Backing-stepping Pre-defined Time Control，BsPdTC）的控制性能，下文将该控制器与有限时间滑模控制器在输入量化条件下进行对比。为保证可对比性，2 种控制器的参数按以下条件选择：首先，考虑姿轨耦合效应，以航天器位置和速度的最大稳定收敛时间作为系统的收敛时间，且初态1 下2 种控制器分别形成闭环系统的收敛时间皆在任务指定时间（120 s）内；初态1 下，反步预时控制器采用表1 控制参数；最后，有限时间滑模控制器控制参数可使得系统收敛时间不大于反步预时控制器。基于上述条件，有限时间滑模控制器参数选择列于表2。

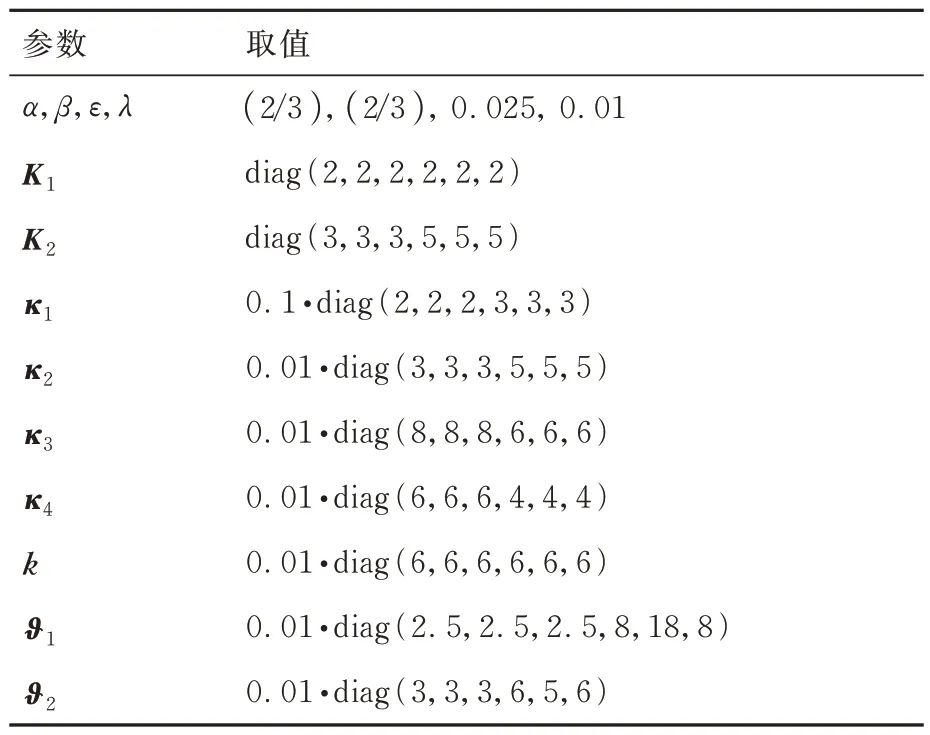
表2 有限时间滑模控制器参数Table 2 Parameters of finite-time sliding mode controller

2 种控制器在控制参数不变、4 组不同初态下进行仿真。4 组初态通过保持故障航天器运动状态不变、改变维护航天器状态的方式设定。维护航天器的初态2：姿态按目标航天器体坐标系的zyx轴相继旋转[119.00°，68.910°，-44.01°]得到，位置在目标航天器体坐标系下[20，-15，-25]Tm处，角速度和平移速度分别为ω=[0.056 550，0.019 537，-0.020 798]T（°）/s 和υ=[1 398.9，-6 962.0，-2 743.1]Tm/s；初态3：姿态按目标航天器体坐标系的zyx轴相继旋转[-19.11°，48.59°，139.11°]得到，位置在目标航天器体坐标系下[25，-20，-30]Tm 处，角速度为ω=[0.043 602，-0.014 725，-0.043 602]T（°）/s，速度为υ=[3 053.3，-5 081.2，4 775.9]Tm/s；初态4：姿态按目标航天器体坐标系的zyx轴相继旋转[0.49°，3.84°，165.49°]得到，位置在目标航天器体坐标系下[30，-25，-35]Tm 处，角速度和速度分别为ω=[0.012 204，-0.010 485，-0.061 306]T（°）/s 和υ=[7 256.4，-1 537.1，1 712.5]Tm/s。

出于简明，4 组初态下两控制器的仿真结果以表和主要变量仿真图形式给出，详见表3 和图12。表3 为两位姿跟踪控制器4 组初态下跟踪性能对比。由表3 可见，初态1 和表2 的控制参数下，有限时间滑模控制器的系统收敛时间约为89.7 s，反步预时控制器的系统收敛时间约为90.5 s，前者和后者基本相同且不大于后者。初态1 时，有限时间滑模控制器下姿态、角速度、位置和速度误差收敛后误差范围可下降到|θi|≤4.77×10-3（°），|ωi|≤1.61×10-2（°）/s，|βi|=5.58×10-5m 和|υi|=8.87×10-5m/s 范围。相应地，反步预时控制器下，各误差状态在进入稳定区间后可满足|θi|≤3.72×10-3（°），|ωi|≤1.60×10-3（°）/s，|βi|=3.28×10-5m 和|υi|=1.02×10-5m/s。初态2 和初态3 时，位姿误差更大。对于系统收敛时间，有限时间滑模控制器在初态3 下达到最大，约为116.5 s，反步预时控制器也在初态3 下最大，约为95.2 s。此两组初态下，反步预时控制器下速度误差的控制精度略提高至10-6量级，其他各跟踪误差的控制精度与初态1 基本为同一量级，遂不赘述。对于初态4，两控制器的误差收敛范围与前3 组初态下同样量级相同，但系统收敛时间反步预时控制器下约为96.8 s，而有限时间滑模控制器下约为127.6 s。

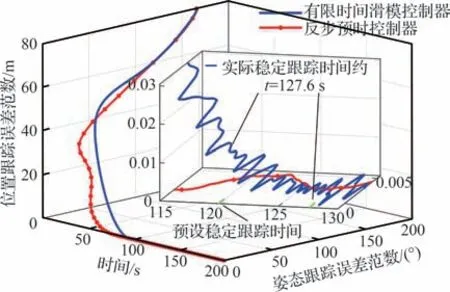
图12 初态4 下位姿跟踪误差对比Fig.12 Comparison of pose tracking error for Initial states 4

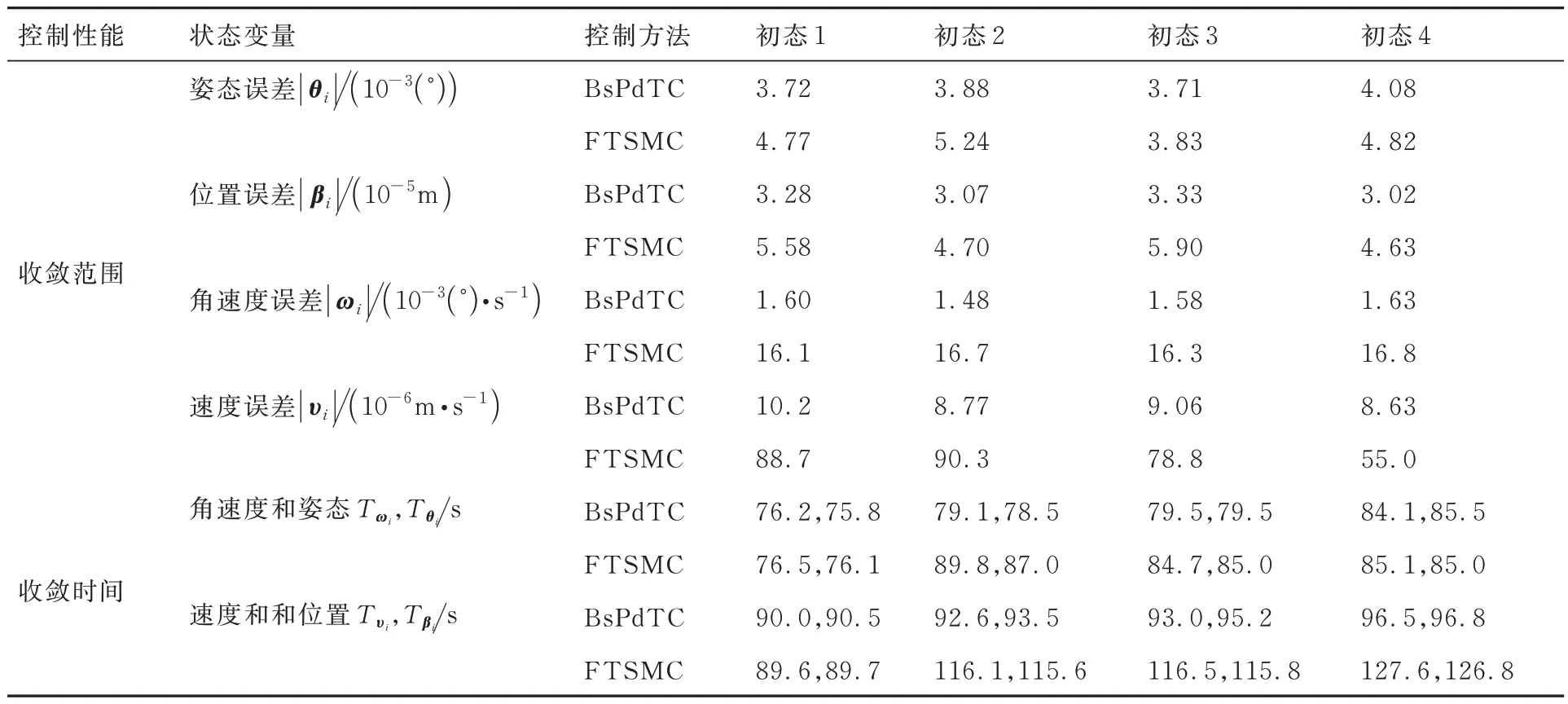
表3 反步预时控制和有限时间滑模控制性能对比Table 3 Performance comparison between back-stepping predefined time controller and finite-time sliding mode controller

特别地，为说明初态4 下两控制器不同的位姿跟踪过程，下面给出了该初态下两控制器位姿误差范数时间响应，曲线见图12。显见，过渡阶段，两控制器下系统位姿误差从约79.9 m 和165.5°开始快速下降。反步预时控制器下位置误差的下降速度快于有限时间滑模控制器，最终，反步预时控制器的系统位姿误差明显先于有限时间滑模控制器进入稳定区间。由115 s 到130 s 的局部放大可见，前者在任务预设定稳定跟踪时间内收敛，而后者在该时间内明显尚未收敛。

由上述结果可知，4 组初态下，2 种控制器的姿态和位置跟踪误差具有同量级的收敛范围，分别为10-3（°）和10-5m。对于系统收敛时间，反步预时控制器在4 组初态下变化范围＜10 s，且皆在任务指定时间内，而有限时间滑模控制器则变化较大，接近40 s，且在较大初始误差（如初态4）时会超出任务预设定收敛时间。由此可知，本文设计的预设时间位姿跟踪控制策略相比有限时间控制策略具有相近的位置和姿态控制精度，但其收敛时间上界与系统初始状态无关。