基于近场动力学的含损伤缺陷Q345钢裂纹扩展分析

李 双，吕海宁，黄小华，杨建民

（1.上海交通大学海洋工程国家重点实验室，上海 200240；2.上海交通大学三亚崖州湾深海科技研究院，海南三亚 572000；3.广西大学防灾与结构安全教育部重点实验室，南宁 530004）

0 引 言

Q345钢材作为一种低合金高强度结构钢，综合性能良好，被广泛应用于船舶与海洋工程结构中，是军辅船、民船的主要结构材料，还是舰艇设备的结构用材料[1-2]。虽然该材料具有较好的塑性性能，但是由初始裂纹扩展造成的低应力脆断是工程结构钢的主要破坏模式[3]，这是由于材料本身缺陷（金属浇筑产生的收缩孔、气泡、杂质，锻压产生的褶层，焊接产生的气孔、夹杂等）或使用过程中造成的损伤（机加工产生的刀伤，运输产生的碰伤，使用过程中的疲劳裂纹和腐蚀裂纹等），使结构内部不可避免地会存在裂纹缺陷，破坏了构件和材料的连续性和均匀性，造成应力集中，在一定条件下微裂纹不断扩展和积聚产生宏观裂纹，最终使材料和结构的工作应力在远低于屈服极限的情况下发生脆性断裂，使工程中存在重大安全隐患，产生不可预估的损失。因此，研究含裂纹缺陷的低合金钢构件的裂纹扩展规律、断裂和破坏行为，掌握其裂纹断裂特性具有重要的学术价值和工程应用背景，且对于军民用船结构的均衡设计、关键钢构件的断裂防护等具有重要意义。

为了研究含裂纹缺陷的钢构件断裂特性和裂纹扩展规律，相关研究者分别采用试验和数值模拟的方法进行了研究。在试验方面，余柳明[4]进行了含裂纹损伤的Q345 钢构件拉伸试验并提出了呈现脆性性能的概率分析方法。张得扬等[2]研究了Q345 钢T 型焊接接头的抗冲击性能，发现焊接拉伸试件的塑性阶段较短，在相同位移载荷下有裂纹缺陷的焊接拉伸试件会提前发生断裂。在数值方面，何书韬等[5]利用弹塑性裂纹及裂纹扩展的理论解析解，探讨了不同裂纹变量对含裂纹损伤的海洋平台结构承载能力的影响。李景阳等[6]根据有限元数值分析方法，研究了双向拉伸载荷作用下的含裂纹金属板的剩余极限强度。刘伟[3]基于线弹性断裂力学理论，借助ANSYS 软件平台，利用APDL 语言编制了专用分析程序，研究了含裂纹损伤金属材料的二维裂纹扩展路径。曾双峰[7]和李玉涛[8]研究了含双边裂纹缺陷的Q345钢在单轴拉伸荷载下的裂纹扩展规律和渐进断裂行为，并采用ABAQUS软件平台进行计算模拟。张婧等[9]应用非线性有限元分析方法，研究了初始变形缺陷对含裂纹加筋板承载力的影响，并讨论了预制裂纹位置和长度对板应力分布特征及变形模式的影响。

由以上分析可知，研究者大多采用有限元及其扩展方法进行结构的断裂模拟，但是有限元法及其他基于连续介质力学理论的数值方法在处理材料不连续问题时，需要额外引入裂纹扩展准则，而且如何克服网格依赖性以及如何解决裂纹萌发和扩展时的非奇异问题仍然是一个挑战。

新兴的近场动力学理论（Peridynamics，PD）[10]的提出弥补了这些不足。PD 以位移的空间积分形式完全重构了传统连续介质力学理论，这种积分型方程在不连续处仍有定义而使其避免了奇异性问题，且PD将物体离散为一系列带质量的物质点，物质点之间通过“键”连接，从而不存在网格依赖性问题。断裂准则通过一个描述连接键状态的记忆函数嵌入本构方程中，能够模拟材料中裂纹自发的萌生和扩展，是一种特别适合模拟材料破坏的力学理论[11]。传统的键基近场动力学方法（Bond-based Peridynamics，BPD）[10，12]只有一个微观模量参数，即键刚度，产生了固定泊松比的限制，在平面应力状态下，泊松比只能是1/3，平面应变状态和三维应力状态下，泊松比只能是1/4[13]。因此，2007年，Silling等[14]提出了能突破泊松比恒定限制的态基PD 方法，但是其需要较高的计算成本并且降低了数值稳定性。2015 年，Prakash 等[15]通过引入一个切向弹簧，提出一种求解平面应力问题的双参数PD 模型，该模型不仅突破了BPD固定泊松比的限制，并且能够保留BPD的简单性和数值实施稳定性，但是该模型主要是为了解决弹脆性破坏问题，对材料受载过程中的非线性行为无法表述，而且也无法反映PD 非局部力的长程力特性。

本文基于近场动力学理论，通过改进Prakash 等[15]提出的双参数PD 方法，提出一种适用于模拟含损伤缺陷的低合金钢断裂的非线性双参数近场动力学模型，重点研究含裂纹损伤的Q345钢拉伸断裂行为，可为船舶设计和结构破坏预测提供参考。

1 双参数PD

传统键基PD 中，宏观连续体在其所在空间域Ω内由大量物质点组成，物质点以初始构型的位置X作为标记，携有体积VX和质量密度ρ。任一物质点X仅在其有限的“域”内通过键与其他物质点X'存在相互作用力f，而与该域以外的物质点不存在任何相互作用。域是以该物质点为中心、以δ为半径的邻域范围HX={X′∈Ω:|X′-X|≤δ} ，根据牛顿第二定律，物质点X在t时刻的运动方程为

式中，ü=∂2u(X,t)/∂t2为加速度，b为体力密度；f为本构力函数，包含了物质点的所有本构信息，表示t时刻单位体积的物质点X'施加于物质点X的体力密度；u和u'分别表示t时刻两物质点的位移。通常采用ξ=X'-X表示初始时刻两物质点的相对位置，η=u'-u表示在t时刻它们的相对位移，则t时刻两物质点的相对位置为ξ+η。

根据Prakash 等[15]提出的双参数PD 方法，假定平面结构内任意两物质点X和X'间通过法向弹簧和切向弹簧连接，法向弹簧是沿着平行键初始方向（ên//ξ=X'-X），切向弹簧是沿着垂直于连接键初始方向（êt⊥ξ），此时，X和X'之间微弹性应变能密度为

式中，cn(ξ,δ)和ct(ξ,δ)分别为法向刚度系数和切向刚度系数，|ξ|为物质点X和X'之间键的原长，且|ξ|=ξ，ηn是相对位移矢量在键初始方向的分量，ηt是相对位移矢量在垂直于连接键初始方向的分量。ω是由于弹簧伸长而储存在连接键中的单位体积应变能密度，称为微弹性应变能密度。物质点X的宏观弹性应变能密度WPD(X)是其近场范围HX内所有与它连接的键内微弹性应变能密度之和，表示为

于是，根据Silling[10]的方法，两物质点X和X'间的作用力密度被推导为

在二维情形下，ên和êt分别表示沿着键初始方向和垂直键初始方向单位矢量，即

该本构力函数是一个不一定与ξ+η共线的矢量，因此，PD的运动方程可表示为

考虑均匀双向应变场下的各向同性均匀体。假设应变无穷小，则每一点的变形梯度为

式中，ε11和ε22分别是材料中任意物质点沿方向1和方向2的应变值。假定ξ是参考构型中与ê1成θ角的任意键，为了简单起见，令ξ= |ξ|，则ξ={ξcosθ,ξsinθ}T。而键ξ变形成ξ+η可通过Fξ给出，即ξ+η={(ε11+ 1)ξcosθ,(ε22+ 1)ξsinθ}T。则相对位移矢量η={ε11ξcosθ,ε22ξsinθ}T，进一步地，相对位移矢量η可以分解为沿法向和切向的分量

值得注意的是，平面应力条件下当材料的泊松比为1/3，平面应变条件下当材料的泊松比为1/4时，切向刚度ct趋近于零，从而退化为类似于传统BPD的单参数模型。

2 改进双参数PD

2.1 考虑PD非局部长程力特性修正

为了考虑PD 物质点间作用强度随物质点距离增大而衰减的客观规律，基于Ha 等[16]在传统BPD模型考虑的能够反映非局部长程力尺寸效应的核函数修正项，推导了双参数键基PD的圆锥形微模量表达式。传统BPD 模型中圆锥形微模量变化函数为g(ξ,δ)=1-(ξ/δ)，因此，考虑非局部长程力特性的双参数键基PD的法向和切向刚度可表达为

式中，cn(0,δ)和ct(0,δ)分别反映两物质点相邻时的点之间法向和切向刚度，g(ξ,δ)反映物质点间长程力的强度随两点间距离变化的规律并且需满足一定的条件方能成立[17]。

因此，式（9）可改写为

同理，二维平面应变状态下，

2.2 双参数PD的非线性本构力函数构建

双参数键基PD模型只能描述弹脆性材料的力学行为，而不能描述材料的非线性受力情况。根据曾双峰[7]和李玉涛[8]针对含裂纹缺陷的Q345 低合金钢在单轴拉伸荷载试验下的载荷-位移曲线，如图1（a）所示，其完整破坏过程是线性与非线性的力学行为，由于初始裂纹的存在，Q345钢裂纹尖端存在高度的应力集中，所以载荷-位移曲线没有明显的屈服平台，其受力过程可划分为线弹性变形OA，非线性强化变形AB和损伤破坏BC三个阶段。

图1 含裂纹缺陷的Q345钢的荷载-位移曲线和双参数PD力函数拟合曲线Fig.1 Load-displacement curve and two-parameter PD force function fitting curve of Q345 steel with crack defects

在近场动力学理论中，近场力与伸长量、荷载与位移均为力与变形的关系，均表述了材料破坏的力学行为，其线性和非线性的关系应是基本一致的。于是，基于石宏顺等[18]将BPD 模型本构力函数划分为线性变形和非线性变形阶段的思想，将含裂纹缺陷的低合金钢的双参数PD本构力函数与试验所得荷载-位移曲线进行拟合，得到双参数PD 的非线性本构力函数曲线，如图1（b）所示。线性段OA和非线性段AC描述键的弹性变形和非线性变形阶段；超过A点以后进入非线性阶段，材料开始发生损伤变形直至最后破坏。

基于双参数PD 方法通过引入非线性本构函数以及损伤模型，使之能够模拟含裂纹损伤的Q345钢损伤累积和断裂行为。由图1（a）可知，荷载-位移曲线的A点是线性变形至非线性变形的过渡点，引入损伤变量D：

式中：s表示键拉伸时的变形，定义为s=(|ξ+η|- |ξ|)/ |ξ|；set表示键拉伸时弹性变形阶段临界伸长量；snt表示键最大拉伸临界伸长量；st表示键拉伸断裂伸长量，对应PD键的断裂。当0 ＜s≤set时，键处在弹性变形阶段，当set＜s≤st时，键进入非线性变形阶段，此时键的损伤开始逐渐积累；当s≥st时，键断裂。在准静态荷载情况下，键拉伸断裂伸长量可表示为st=αft/E，键的断裂意味着裂纹的形成。因此，受拉荷载下Q345钢线性变形和非线性变形阶段的本构力函数基本形式可表示为

将式（19）代入式（20），可得含裂纹损伤Q345钢拉伸断裂的双参数PD非线性本构力函数表达式：

在交变荷载情况下，PD 疲劳裂纹的扩展仍采用上述改进的PD 计算方法，但是键疲劳断裂准则取代准静态荷载下的断裂准则。在疲劳断裂准则中，单次的荷载无法直接产生键断裂效应，通过对模型的一次准静态分析来处理一次荷载循环，得到这一次荷载循环中键的损伤量。随着交变荷载循环次数的增加，键的损伤逐步累积，当达到一定的条件时，键断裂，从而得到疲劳裂纹的萌生和扩展。因此，可赋予每个键“剩余寿命”λ的概念，其初始值与循环荷载次数N的关系[19]如下：

式中：ε为键伸长率的变化值；smax和smin分别为一次加载过程中键伸长率的最大值和最小值，通过准静态分析得到；R为应力比；A和p均为可通过实验数据拟合得到的待定常数。PD 采用标量函数μ来表达键的损伤情况[12]，键未发生断裂时，μ=1；键断裂时，两个物质点相互作用永久消失，此时μ=0。交变荷载情况下，在标量函数μ中引入“剩余寿命”λ参数，将μ改写为

为了表征任意质点位置处的损伤程度，可基于标量函数μ定义每个质点的损伤指数ψ，当ψ=0时表示材料未发生损伤，ψ=1时表示材料完全损伤，可表示为

3 误差分析

为了验证提出的改进双参数PD 模型的计算精度，通过数值解与解析解进行对比分析。采用长1 m、宽0.5 m 的长方形薄板，弹性模量E=200 GPa，密度ρ=7850 kg/m3，几何参数和材料参数除泊松比外，与Madenci 等[20]采用的误差分析算例相同，薄板被离散为100×50 个物质点，物质点间距Δ=0.1 mm，邻域半径δ=3.015Δ，沿矩形短边施加的单轴应力荷载为p=200 MPa，应力边界条件的施加方式是从薄板边界区域上以体力密度的形式施加在板内物质点上。因为双参数PD 模型能够突破传统BPD模型固定泊松比的限制，该算例取材料泊松比ν等于0.1、0.15、0.2、0.25、0.3、1/3分别进行计算。

根据弹性力学基本理论，二维平面x和y位移解析解计算公式为ux(x,y=0)=px/E，uy(x= 0,y) =-νpy/E。x和y位移的数值解ux*、uy*与解析解ux、uy的相对误差计算公式为ex=(ux*-ux)/ux，ey=(uy*-uy)/uy，其中，ex、ey分别表示x和y位移的相对误差。

当泊松比ν=0.3 时，改进的双参数PD 模型与Prakash 等[15]原双参数PD 模型计算的薄板沿受力x方向的误差位移云图如图2所示。由图可知，改进的双参数PD 模型沿受力方向的数值解与解析解的最大相对误差为1.85%，而原双参数PD模型最大相对误差为2.44%。薄板内部的相对误差也从0.43%提升到了0.1%。

图2 双参数PD模型相对误差云图Fig.2 Contours of two-parameter PD model relative errors

图3 给出了泊松比ν分别取0.1、0.15、0.2、0.25、0.3、1/3情况下的两种双参数PD 模型沿薄板受力方向的最大相对误差。由图3 可知，无论材料泊松比取何值，改进的双参数PD 模型总能进一步提高计算精度，减少误差；并且随着材料泊松比的增大，计算误差有逐渐增大的趋势，但最大的相对误差也仅有2.54%，此时泊松比ν=1/3。

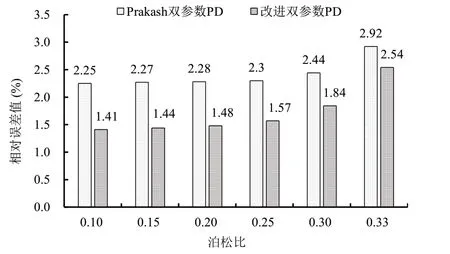
图3 不同泊松比情况下两种双参数PD模型的最大相对误差Fig.3 Maximum relative errors of two two-parameter PD models with different Poisson's ratios

4 含损伤缺陷Q345钢裂纹扩展模拟

为了验证改进的非线性双参数PD 方法，将试验结果和数值模拟仿真得到的裂纹扩展结果进行对比分析。采用几何参数和材料参数与文献[7-8]相同的低合金高强度Q345 结构钢，有效几何尺寸长度、宽度和厚度分别为70 mm、40 mm 和4 mm，试件双边缘预制穿透型裂纹，裂纹宽度为2 mm，如图4 所示。材料弹性模量E=203 GPa，泊松比ν=0.3，质量密度ρ=7850 kg/m3，极限抗拉强度ft=572 MPa，将试件进行离散，取物质点间距Δ=0.5 mm，邻域半径δ=3.015Δ。整个模拟过程中在试件短边采用位移加载，每一个加载步在试件两端施加一个增量为Δu=1.5×10-7mm 的位移，为了得到每一步位移的稳态解，采用动态松弛法[20]，时间步长取Δt=1.0。最大拉伸临界伸长量与材料抗拉强度相关，snt=ft/E=2.82×10-3。通过PD 数值计算方法，以程序设计的方式实现了对该材料破坏的模拟。

图4 预制双边裂纹的Q345钢试件示意图Fig.4 Sketch of the Q345 steel specimen with double-edge notch

4.1 不同裂纹间距双边裂纹扩展分析

在本节中，试件的双边预制裂纹互相平行，双裂纹长度l1=l2=10 mm，α=0°，裂纹纵向间距d分别为0 mm、10 mm和20 mm。

图5 展示了d为10 mm 和20 mm 时Q345 钢试件的裂纹扩展模式。由图5（a）可知，d=10 mm 时，试件在t=2100 时间步双预制缺陷尖端开始起裂，裂纹沿垂直加载方向生长，到达t=2900 时，两尖端的水平距离和竖向距离接近相等，裂纹改变扩展方向，沿与水平方向大约45°方向扩展，至t=3700 时，最终双裂纹串接，试件被拉断。由图5（b）可知，d=20 mm 时，试件在t=2230 时间步双缺陷尖端开始起裂，试件裂纹单独沿垂直加载方向一直扩展，双裂纹互不影响，不发生交汇，各自扩展至试件边缘，至t=5550 时间步，最终断裂破坏。由模拟可知，随着裂纹间距的增大，双边裂纹从开始扩展至完全破坏的时间有逐渐增大的趋势。

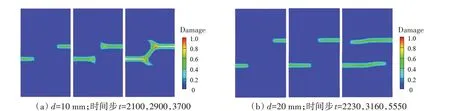
图5 不同裂纹间距的试件裂纹扩展示意图Fig.5 Crack propagation of specimens with different crack distances

图6展示了采用本文改进双参数PD方法和Zhao等[21]采用态基PD方法模拟的裂纹间距分别为d=0 mm，d=10 mm 和d=20 mm 时的Q345 钢试件的最终断裂形态；图7 展示了试验试件的三种裂纹间距的预制缺陷布置形式和拉伸断裂试验结果。对比可知，PD 数值模拟仿真得到的裂纹启裂位置、扩展方向以及最终破坏形态与试样试验产生的结果保持了很好的一致性；与Zhao等[21]采用态基PD模拟的拉伸断裂结果也吻合较好。证明了提出的双参数PD 模型用于含损伤缺陷的Q345钢的裂纹扩展和拉伸断裂破坏分析是可行的。

图6 不同裂纹间距Q345钢裂纹生长路径的两种数值模拟结果对比Fig.6 Comparison of numerical simulation results of Q345 steel with different crack distances by two PD methods

图7 不同裂纹间距Q345钢的裂纹布置形式和拉伸断裂试验结果［7］Fig.7 Experimental results of Q345 steel specimens with different crack distances

4.2 不同裂纹长度双边裂纹扩展分析

在本节中，试件的双边预制裂纹位于试件的中轴线上，双裂纹间距d=0 mm，α=0°，裂纹长度分别为l1=l2=5 mm，l1=5 mm、l2=10 mm和l1=l2=10 mm。

图8 展示了l1=l2=5 mm 和l1=5 mm、l2=10 mm 时Q345钢试件的裂纹扩展模式。由图8（a）可知，l1=l2=5 mm 时，试件在t=2400时间步双预制缺陷尖端开始起裂，双裂纹沿垂直加载方向对称扩展，至t=3700 时裂纹进一步水平生长，到达t=4100 时，双裂纹尖端在试件中心交汇。由图8（b）可知，l1=5 mm、l2=10 mm时，试件在t=2100时间步l2裂纹率先萌发并沿垂直加载的方向扩展，之后l1裂纹扩展，至t=3200时，l2裂纹率先到达试件中心位置，最后至t=3700，双裂纹在靠近l1裂纹尖端附近交汇并贯穿整个试件。由模拟可知，当双边裂纹对称布置时，在荷载作用下，裂纹对称扩展；对称裂纹越长，试件有更早破坏的趋势；当双边裂纹非对称布置时，裂纹首先沿预制缺陷更长的一侧扩展，然后在短边预制裂纹处交汇贯通。

图8 不同裂纹长度的试件裂纹扩展示意图Fig.8 Crack propagation of specimens with different crack lengths

图9 展示了采用本文改进双参数PD 方法和试验方法获得的三种不同双裂纹长度l1=l2=5 mm，l1=5 mm、l2=10 mm和l1=l2=10 mm的裂纹生长路径。在模拟过程中，当裂纹尖端的损伤值接近1时，物质点间的PD 力消失，裂纹沿垂直加载方向扩展，随着荷载的增加，损伤部位逐渐扩大，最终贯穿整个试件。通过图9（a）和9（b）对比可知，数值模拟和试验结果的裂纹扩展路径保持一致。

图9 不同裂纹长度Q345钢裂纹生长路径的数值模拟和试验结果对比Fig.9 Comparison of numerical and experimental results of Q345 steel with different crack lengths

4.3 不同裂纹角度双边裂纹扩展分析

在本节中，试件的双边分别预制水平裂纹和斜裂纹，双裂纹长度l1=10 mm，l2=10 mm，裂纹纵向间距d=10 mm。试件倾斜裂纹角度分别为α=30°，α=45°和α=60°。

图10（a）展示了α=30°时Q345 钢试件在t为2220、2950 和4050 时间步的裂纹扩展模式；图10（b）展示了α=60°时Q345钢试件在t为2150、3100和4120时间步的裂纹扩展模式。两种试件的裂纹扩展模式和最终破坏模式相似，首先，裂纹从预制倾斜裂纹的尖端扩展，随后，预制水平裂纹的尖端开始扩展，双裂纹沿垂直加载方向生长，当两尖端的水平距离和竖向距离接近相等时，裂纹改变扩展方向，沿与水平方向大约45°方向扩展，最终双裂纹串接，试件被拉断。由于预制裂纹倾角的改变并没有改变双边预制裂尖的间距，因此裂纹角度的增大，对裂纹扩展模式和试件整体贯通时间并无较大影响。

图10 不同裂纹角度的试件裂纹扩展示意图Fig.10 Crack propagation of specimens with different crack angles

图11展示了采用本文改进双参数PD方法和试验方法获得的三种不同双裂纹角度α=30°，α=45°和α=60°时的试件破坏形态。对比可知，PD 数值结果与试验结果保持了很好的一致性，但也存在一定差异。主要原因在于：PD 理论认为材料是理想均匀各向同性的，而试样实际上存在非均匀性和成分性能等差异；其次，PD 理论是从宏观尺度来描述材料破坏，未从材料的微观和细观尺度分析原子分子、自身存在的微孔洞、微裂纹及晶界对材料破坏的影响[18]。

图11 不同裂纹角度Q345钢裂纹生长路径的数值模拟和试验结果对比Fig.11 Comparison of numerical and experimental results of Q345 steel with different crack angles

4.4 交变荷载下中心斜裂纹板的裂纹扩展模拟

采用本文PD 模型对文献[22-23]中斜裂纹板的疲劳裂纹扩展进行模拟。试件尺寸为300 mm×100 mm×2 mm，中心有一穿透斜裂纹，裂纹长度为10 mm，与垂直中心线的夹角为60°，弹性模量E=72 GPa，泊松比ν=0.3。平板上下预留夹持端并施加拉—拉交变荷载，最大应力σmax=70 MPa，应力比R=0.1，将其简化为平面应力问题并建立PD疲劳模型，物质点间距Δ=1mm，δ=3.015Δ，共计29 988个真实物质点，在板顶端一层物质点上施加70 MPa的最大循环载荷，对平板下端3层物质点的位移进行约束，采用与文献[23]相同的模型参数和最大循环加载次数：模型参数A=6450，p=2.86，设置最大循环加载次数N=139 610。

使用本文改进的PD 模型，对交变荷载下斜裂纹板内疲劳裂纹扩展进行模拟，裂纹扩展路径结果如图12（a）所示，疲劳裂纹自中心斜裂纹两尖端处向两侧扩展，且两侧裂纹扩展路径均近似呈一水平直线。图12（b）-（d）分别展示了采用扩展有限元法（XFEM）[22]、态基PD 方法[23]的模拟结果和试验结果[22]。对比图12（a）与图12（b）-（d）可得，本文模拟结果与试验结果和文献模拟结果的裂纹扩展路径基本一致。在相同循环加载次数下，将中心斜裂纹左右两尖端的扩展长度与初始裂纹长度相加，得到疲劳裂纹总长度a与循环荷载次数N的a-N曲线，将其与试验结果[22]和已有文献结果[22-23]进行比较（图13），结果吻合较好，证明了本文PD模型模拟交变荷载情况下裂纹扩展的准确性。

图12 交变荷载下试件裂纹扩展路径的数值模拟和试验及文献结果对比Fig.12 Comparison of numerical and experimental results of specimen under alternating load

图13 荷载循环次数与裂纹长度的关系Fig.13 Relationship between the number of load cycles and the crack lengths

5 结 论

近场动力学理论采用积分方程替代传统微分方程从而避免了在不连续处产生的奇异性问题且不存在网格依赖性，特别适用于研究材料破坏问题。本文基于Prakash 等[15]提出的PD 方法，通过引入长程力函数修正非线性损伤模型，提出了适用于含裂纹缺陷Q345 钢裂纹扩展的双参数PD 模型。通过误差分析、准静态荷载和交变荷载情形下含初始缺陷钢构件的裂纹扩展和断裂模拟分析，得出以下结论：

（1）改进的双参数PD 模型减小了原始模型的计算误差，并且发现，随着材料泊松比的增大，数值解与解析解的相对误差有增大的趋势。

（2）准静态荷载下，PD数值模拟的裂纹开裂位置、扩展方向和最终破坏路径与试验结果和其它数值方法所得模拟结果吻合较好；交变荷载下，PD 数值模拟的裂纹扩展长度与循环荷载次数的关系与试验结果和已有文献数值结果保持一致；证明了本文提出模型对含缺陷的Q345钢进行裂纹扩展分析的适用性和准确性。

（3）在一定条件下，试件的破坏形态与预制缺陷的相对位置有关，而初始裂纹缺陷的长度和角度对最终裂纹扩展路径影响虽不大，但对试件整体贯通破坏时间产生一定的影响。