基于连续介质损伤力学的钛合金耐压球壳极限强度分析

张博文，万正权，赵 青，徐 强，张爱锋

（1.中国船舶科学研究中心，江苏无锡 214082；2.深海技术科学太湖实验室，江苏无锡 214082）

0 引 言

钛合金比强度高、耐腐蚀性好，是优良的轻质高强“海洋金属”，已广泛应用于深海载人潜水器等深海装备的耐压结构中。但钛合金材料塑韧性指标相对较低，导致其对微观缺陷更加敏感。如图1所示，相同强度等级的钛合金耐压球壳[1]的破坏形式与高强钢[2]迥然不同，钛合金结构呈现明显的内溃式破碎。精准预测钛合金材料与结构的损伤、失效以及结构极限强度是开展深海载人装备结构技术研究的关键，对于指导深海装备用钛合金性能的提升与改进具有重要意义。

图1 耐压球壳失效模式[2，30]Fig.1 Failure modes of pressure hulls

自上个世纪60 年代以来，大量学者针对材料的本构关系与损伤模型展开了研究工作[3-7]，其中根据损伤是否影响材料塑性阶段的力学行为，损伤模型大致可以分为非耦合类和耦合类。非耦合类模型结构形式简单，模型参数易于确定，但由于没有考虑损伤扩展对材料力学行为的影响，导致其使用范围受限，代表模型有Johnson-Cook（J-C）模型[8]、Wierzbicki-Bao 模型[9-10]以及L-H 模型[11-13]等。耦合类损伤模型中最具影响力的代表是Gurson-Tvergaard-Needleman（GTN）模型[14-16]和连续介质力学（Continuum Damage Mechanics，CDM）模型[17]。GTN模型材料参数关系复杂，导致材料参数的确定较为困难，大多需通过人为调试，此外经典的GTN 模型中损伤的累积并不影响材料的弹性模量，没有真正做到弹塑性与损伤的强耦合。CDM模型根据连续介质力学与热力学的唯象学方法研究损伤随变形发展最后导致破坏的力学过程，通过引入损伤变量来描述含缺陷材料的力学响应及材料自身的劣化过程，并从宏观上研究损伤的发展对材料宏观力学性能的影响以及材料损伤演化过程和规律，以便预测材料的变形、破坏和使用寿命。Bonora 等[18]在Lemaitre 研究的基础上对损伤演化方程进行了改进，提出了考虑非线性的损伤势函数，并通过了实验验证，预测精度相比Lemaitre 模型有所提升。王治磊等[19]利用有限元软件研究了SUS304 不锈钢的损伤和韧性断裂行为，研究表明Lemaitre 模型比Johnson-Cook 模型具有更高的精度。Bonora等[20]与Testa等[21]深入研究了损伤起始应变（孔洞形核应变）与应力三轴度的关系，发现随着应力三轴度的增加孔洞形核塑性应变越低，并修正了形核应变与应力状态的关系，更新了非线性CDM 模型，使之物理意义更加清晰。Li等[22]考虑了应力三轴度、罗德参数以及剪切应力对损伤累积的影响，进一步修正了Lemaitre 模型，并通过有限元模拟与实验证明了修正模型对铝合金复杂成形过程损伤行为预测的准确性。张毅等[23-24]将CDM 模型应用在聚乙烯材料的断裂行为预测上，模拟结果与实验结果吻合良好。

现有深潜器耐压球壳结构极限强度分析是在板壳理论和弹塑性力学的理论框架下，随着工作潜深与壳板厚度的增加，力学模型由薄壳结构力学模型渐变为厚壳力学模型。现有潜水器规范不适用于厚球壳结构的极限强度分析[25]，经大量学者广泛研究[26-27，29]，引入了材料非线性和几何缺陷的有限元技术可以预报厚球壳结构的极限强度。然而，为了简化计算，众多学者普遍选用双线性的理想弹塑性材料本构关系模型，未充分考虑加载过程中材料力学性能硬化与软化过程。本文将在耐压球壳极限强度有限元分析技术的基础上，研究Bonora连续介质损伤力学模型[28]，模拟典型球壳结构的失效模式与破坏压力，为后续深海钛合金耐压结构精细化数值仿真技术研究提供基础。

1 损伤模型理论

材料或结构失效是由于微损伤增长所致，属于不可逆能量耗散过程。连续介质损伤力学采用损伤变量D从宏观层面描述材料的损伤演化过程。损伤变量定义为材料中存在的不可逆缺陷的比率，D=0表示无损伤的完整材料，D=Dcr表示材料完全损伤失去承载能力，Dcr表示临界损伤变量，一般认为等于1，但是学者普遍认为Dcr＜1。由于损伤变量D是一个难以直接进行实验测量的量，一般只能间接测量，目前最常用的方法是利用杨氏模量的退化来测量损伤，如式（1）所示，但由于损伤对材料特性的影响是通过微结构的变化实现的，一般情况下组织不敏感量（如材料变形特性）对损伤不敏感，而组织敏感量（如强度特性）对损伤非常敏感。

式中，ED为材料损伤后的有效弹性模量，E0为无损材料的弹性模量。

由于损伤导致材料组织结构的有效承载面积有所减少，有效应力则相应会随之增加，根据等效应变假设，作用在损伤材料上的名义应力所产生的应变等于作用在相应无损材料上有效应力所产生的应变。

式中，σeff为有效应力，σ为实际应力。根据Lemaitre实验观察，发现损伤和材料的弹性相关，于是把材料耗散势函数分为不耦合的弹性部分和塑性部分，只把损伤引入到弹性势函数（损伤耗散势函数FD）中，塑性势函数fp不反应损伤，如式（3）所示。

Bonora在Lemaitre准则的基础上提出了考虑损伤演化的损伤耗散势函数：

式中，S0是材料参数，n是材料硬化参数，α是决定损伤演化曲线形状的损伤指数，Ēp为累积等效塑性应变，Y表示应变能释放率，

式中，σeq表示等效应力，η表示应力三轴度（静水压力与等效应力之比），μ为泊松比。

根据Lemaitre准则，损伤演化的动力学规律可以描述为

在比例加载的情况下，损伤变量可以表达为

式中，εˉth为单轴拉伸损伤起始时的等效塑性应变，εˉcr为单轴拉伸失效时的等效塑性应变，pth为材料损伤起始时的等效塑性应变，为了简化计算，通常情况下认为材料损伤起始时的等效塑性应变近似等于单轴拉伸损伤起始时的等效塑性应变。从式（7）可以看出，Bonora模型通过应变能释放率引入了应力三轴度的影响，模型中的主要参数分别为εˉth、εˉcr、Dcr和α。

2 材料试验

试验材料为TA31钛合金，其主要成分如表1所示。

表1 钛合金主要化学成分（%）Tab.1 Main chemical composition of titanium alloy（%）

试样根据国家标准GB/T 228.1-2010 进行制备，形状与尺寸如图2所示。

图2 钛合金标准试样Fig.2 Sample of titanium alloy

为测量损伤参数，进行两类试验：单向拉伸试验和拉伸加载卸载试验，每类试验进行3 组重复性试验。两类试验的试验加载设备均采用UTM 5105 型电子万能试验机，试验机最大拉力为100 kN，在每个试件中部悬挂电子引伸计，标距为25 mm。试验加载均采用位移控制，加载速率设定为2 mm/min。

首先，对TA31钛合金标准试样进行单向拉伸至断裂，获得TA31钛合金载荷位移曲线；随后，将载荷位移曲线塑性段进行20 等分，分割点作为拉伸加载卸载试验时的加载位置，开始时将试样拉伸到第1 个分割点位置后进行卸载，当载荷卸载至0 后再拉伸至下个分割点位置，如此反复进行加载卸载实验，根据每个卸载段杨氏模量衰减变化规律测定式（1）中的损伤因子。

3 损伤参数分析

在拉伸过程中材料分别经历了线弹性阶段、塑性硬化阶段、颈缩阶段以及失效断裂。塑性硬化模型如Johnson-Cook（J-C）模型，本文仅考虑室温准静态过程，因此忽略应变速率和温度的影响，简化公式为

式中，A为材料的屈服极限，B和n分别为材料应变硬化模量和硬化指数。在材料进入塑性初期，材料内部孔洞缺陷形核，但所占比例较少，并不影响材料的宏观力学性能，此时J-C 硬化模型可以较好地模拟材料硬化阶段的应力应变响应。随着材料内部孔洞缺陷扩张积累到一定程度，有效承载面积逐渐减少，有效应力逐渐增加，材料宏观软化行为开始凸显，未考虑损伤因素的J-C 模型会高估材料的硬化行为。当仿真结果与试验结果出现分离时，定义此刻为损伤起始位置，截面中心位置的等效塑性应变为εˉth，如图3 所示。当材料内部的微小单元出现孔洞贯穿形成宏观裂纹时，结构承载能力丧失，在裂纹发生失稳扩展后，载荷骤降至0。

图3 TA31钛合金光滑圆棒式样载荷位移曲线Fig.3 The load-displacement curve of TA31 titanium alloy with smooth round bar sample

损伤指数α决定了损伤演化曲线的形状，对于给定的εˉcr和Dcr，如图4（a）所示，α越大损伤演化曲线越陡峭，断裂时刻引伸计位移和临界断裂载荷越小，材料软化速率越快，而当α减小时载荷位移曲线趋于平缓，α趋近于0 时，D也趋近于0，表明材料无软化行为，此时，基于Bonora 模型预测的载荷位移曲线与J-C模型一致。上述规律表明，损伤指数α与材料内部孔洞缺陷的形核速率有关：当α较大，且塑性应变超过门槛值时，孔洞缺陷扩张速率逐渐增大，材料的有效承载面积加速减少，表明材料内部孔洞较多且塑韧性能较差；当α较小时，孔洞缺陷形核速率较慢，材料力学性能变化较为平缓，材料内部孔洞较少，韧塑性能较好。

图4 载荷位移曲线Fig.4 Load-displacement curve

Dcr是临界损伤因子，取值介于[0，1]，损伤因子的理论上限是1，表示材料完全丧失承载能力，式（2）中的有效应力趋近于无限大。Dcr=0 表示材料无损伤行为，载荷位移曲线与不考虑损伤演化行为的J-C模型一致，如图4（b）所示，临界损伤因子Dcr对载荷位移曲线的影响波动较损伤指数α小。

部分学者[20-21，28]认为Dcr=1 是理论情况，实际材料失效时的损伤临界值小于1，损伤临界值与材料内部孔洞密度有关，不同材料损伤临界值差别较大。但随着外部载荷的增加，材料内部孔洞缺陷动态演化，由于孔洞分布与生长的随机性，导致很难准确地测量，不同学者利用超声与射线技术测量得到的杨氏模量与单位体积孔洞数量之间的经验公式会存在差别，针对相同材料得到的损伤临界值也会不同。当Dcr＜1 时，有效应力不会出现奇异解，在加载历程中积分点处的损伤值达到临界值而单元被删除时，积分点处的应力不会出现奇异，无法模拟因微缺陷演化而导致的应力集中现象。因此，本文认为在有限元模拟时Dcr=1 具有较明确的物理意义，一个单元为模型最小宏观尺度，当单元内部等效塑性应变达到起始值εˉth时，单元内部缺陷演化加速，表现为力学性能软化；当等效塑性应变达到临界值εˉcr时，Dcr=1，单元失去承载能力，积分点位置有效应力发生奇异，采用单元删除技术，将Dcr=1 的单元删除，可以进一步模拟裂纹扩展的过程及应力应变演化规律。

εˉcr是材料失效临界时刻的等效塑性应变，试验中得到的塑性应变是引伸计标距范围内的平均值，加载过程中试样不同截面的缺陷孔洞分布不均匀，最大塑性应变发生在断裂截面的中心位置大于0.4，最小塑性应变发生在引伸计夹持端0.02左右，根据试验推算得到的平均断裂塑性应变为0.14，如图5 所示。中心位置等效塑性应变达到失效临界值时，边缘位置尚未达到损伤起始临界值，而结构失效判据是敏感参量，因此，在Bonora 模型中εˉcr设定为最小截面中心位置的最大塑性应变。

图5 应力应变曲线Fig.5 Curve of stress-strain

4 损伤参数校准

4.1 参数校准方法

根据上述分析，本文提出了一种Bonora损伤模型参数校准方法，如图6所示。

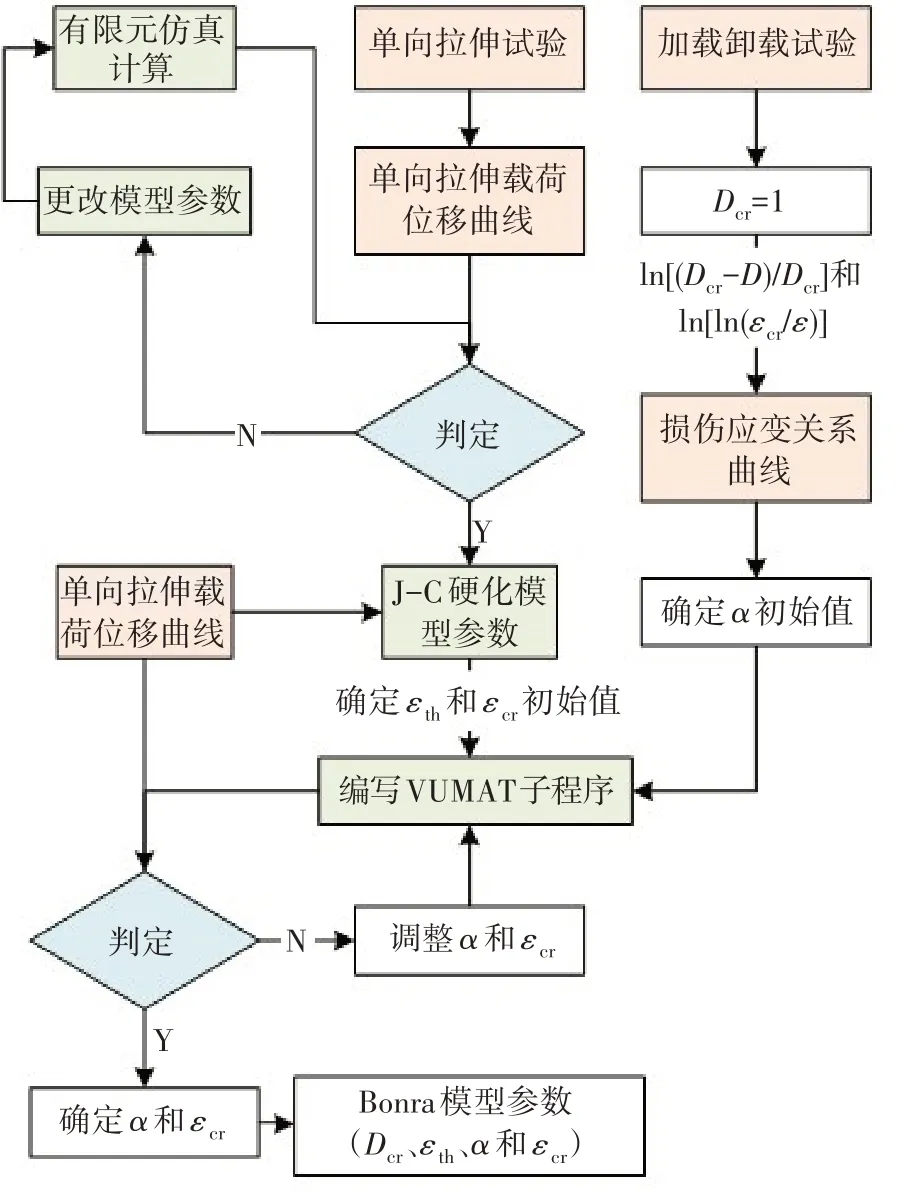
图6 模型参数校准流程图Fig.6 Flow chart of model parameter calibration

首先，基于单向拉伸试验获得的载荷位移曲线校准J-C 硬化模型，根据仿真计算得到的载荷位移曲线与试验值比对，确定损伤起始时刻等效塑性应变与损伤临界时刻等效塑性应变初始值。

然后，根据加载卸载试验获得的真实应力应变关系换算得到损伤变量与等效塑性应变关系，认定损伤临界值为1，根据损伤变量演化趋势，换算得到损伤指数初始值。

最后，将Bonora 损伤模型通过VUMAT 子程序嵌入到ABAQUS 有限元软件中，将上述初始参数代入模型，如果计算得到的载荷位移曲线和断裂失效位置与试验值相吻合，则认为上述参数为准确值，反之则修改参数重新计算，直到与试验值吻合为止。

4.2 参数校准

本文材料硬化模型选用J-C 模型（如式（8）所示），基于最小二乘法并根据颈缩以前阶段的单向拉伸试验数据（平均值）进行拟合，得到模型参数如表2所示

表2 模型参数Tab.2 Model parameters

通过试验数据处理，可以得到加载卸载状态下真实应力应变曲线，如图7 所示，在最后一次加载进入塑性后试件发生断裂，通过最后一次卸载加载杨氏模量变化得到的损伤因子最大值为0.1，表明当损伤变量超过0.1时，孔洞扩张呈现加速状态，大孔洞之间相互贯通最终导致整个截面丧失承载能力。但由于加载卸载试验测得的损伤因子是标距范围内的平均值，属于钝感参量，而在有限元计算时引入的损伤因子，表征微小单元积分点位置的材料软化特性，当损伤因子达到损伤临界值时，该单元有效应力发生奇异，单元丧失承载能力被删除，属于敏感参量。当一个单元被删除时，周围单元发生应力重分配，截面仍具有一定的承载能力。因此，基于加载卸载试验得到的杨氏模量衰减规律滞后于基于有限元方法计算得到的结果，加载卸载试验仅能反应损伤变量的演化趋势，无法准确测定最终的损伤临界值。

图7 TA31钛合金拉伸加载卸载真应力应变曲线Fig.7 True stress-strain curve of TA31 titanium alloy under tensile loading and unloading

试验所用试样为标准圆棒拉伸试样，平均应力三轴度为1/3，代入式（7），经代数变换得到如下线性表达式：

加载卸载试验测得的ε～D为平均统计值，但其相互间比例关系与有限元计算值一致，因此基于式（9），将试验值代入可以推算得到损伤指数初始值α0，如图8所示，其平均值为0.0359。

图8 塑性应变与损伤因子关系Fig.8 Relationship between plastic strain and damage factor

将损伤指数初始值代入到Bonora模型中，进行迭代运算，确定最终模型参数，如表2 所示。基于Bonora 模型仿真计算得到的载荷位移曲线与试验值对比，如图9所示，起裂点在最小截面中心位置，随着载荷增加逐渐向边缘扩展，在截面边缘形成近似45°斜切面。从图中可以看出，在J-C 塑性模型的基础上，Bonora 模型可以延伸模拟材料软化行为，有助于精准模拟结构的极限强度。

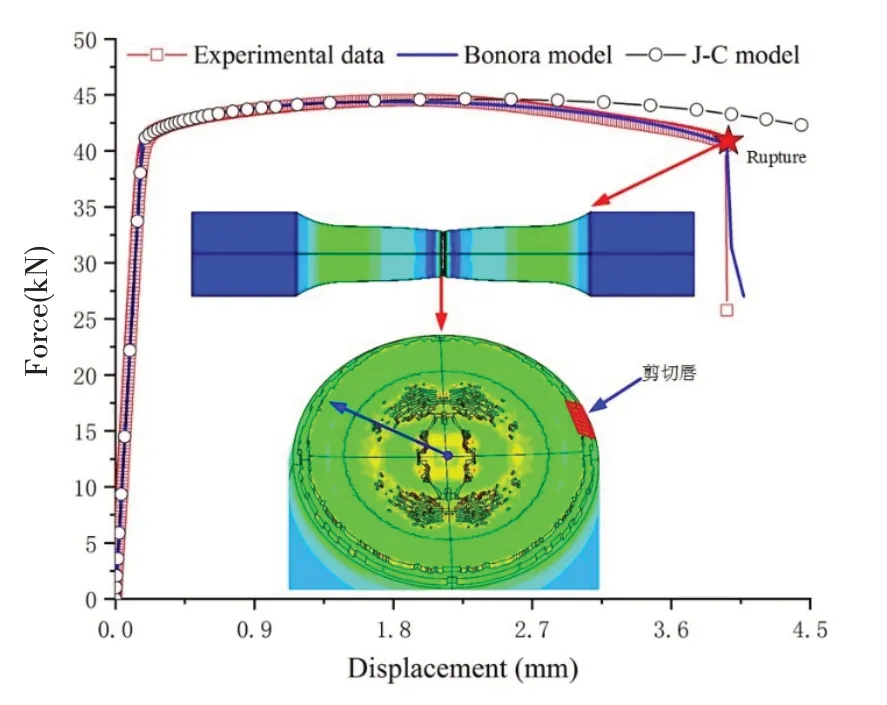
图9 仿真计算与试验值对比Fig.9 Comparison between simulation and test values

5 耐压球壳极限强度分析

刚度破坏（失稳）与强度破坏是耐压球壳结构失效的主要形式，薄球壳结构弹性失稳压力与结构厚径比（厚度t/半径R）的平方成正比[29]。厚径比较低时，球壳结构失效模式以刚度破坏为主；而当厚径比较大时，球壳结构弹性失稳压力远高于实际破坏压力，材料非线性与初始几何缺陷的影响不能忽视，强度破坏起主导作用。1996 版中国船级社《潜水系统和潜水器入级建造规范》给出了外压球壳承载能力的计算方法。在此基础上，潘彬彬[1，30]开展了钛合金球壳结构极限承载能力模型试验与仿真计算分析，基于大量有限元仿真计算，提出了以材料拉伸极限σb为材料输入的钛合金球壳结构极限承载能力计算公式，该公式经调整被接受为2018版中国船级社《潜水系统和潜水器入级规范》[31]（简称“潜规2018”）。石佳睿等[32]基于强度计算公式，提出了以材料屈服极限σs为材料输入的考虑球壳开孔和初始缺陷的极限强度计算公式。熊志鑫等[33-34]基于切线模量理论提出了一种耐压球壳极限强度的简化算法，并深入研究了初始缺陷对耐压球壳结构极限强度的影响规律。上述研究工作侧重研究球壳结构几何初挠度偏差对结构极限承载能力的影响，未在数值仿真计算模型中考虑材料强化及损伤演化带来的材料非线性影响，导致屈服强度或抗拉强度相同，但屈强比不同的材料，通过弹塑性模型计算得到的结构极限强度是相同的。尽管基于上述公式的预报误差在可接受范围内，但由于缺少考虑材料的非线性行为，无法准确指导深海装备用钛合金材料性能的优化与改进。因此，本文将Bonora模型引入到球壳结构的极限承载能力分析中，充分考虑材料强化及软化行为对结构极限承载能力的影响。

本文依据Pan 等[30]研究工作中TA31 钛合金（又名Ti80）耐压球壳缩比模型压力筒考核试验（具体模型参数详见文献[30]），开展Bonora 模型扩展应用研究，利用有限元软件ABAQUS 对典型球壳结构进行数值仿真计算，首先开展球壳结构屈曲模态分析，随后根据实测缺陷幅值将1 阶屈曲模态转换为几何缺陷引入到ABAQUS/Explicit 模块中，编写考虑Bonora 损伤模型的用户自定义子程序进行非线性有限元分析。计算结果如图10 所示，当静水外压载荷达到57.39 MPa 时，在模态缺陷凹坑边缘位置损伤因子升至临界值Dcr=1，单元被删除，凹坑中心位置单元Mises 应力达到最大值，随着载荷继续增加，凹坑中心位置单元Mises应力骤降，裂纹贯穿并快速扩展致模型破坏。

图10 基于Bonora模型的球壳结构典型位置应力应变Fig.10 Stress-strain of spherical shell based on Bonora model

为了对比分析，在ABAQUS/Riks模块中不考虑材料非线性本构关系模型，设定材料双线性各向同性硬化参数，材料极限强度分别设定为σs和σb，切线模量设定为0 MPa[35]。当耐压球壳凹坑位置大范围进入塑性时，结构丧失承载能力，达到结构极限强度，节点位移随载荷下降而持续增加。计算结果汇总于表3，结果表明，当材料极限强度增加时，结构极限承载能力提升近7.2%，而耐压球壳模型实际破坏压力介于图11所示计算区间，误差不超过5%。强度破坏是在大潜深环境下厚球壳结构的主要失效模式，材料非线性行为的影响权重随着厚径比的增加而逐渐增加。计算结果表明，基于Bonora 模型的耐压球壳结构极限承载能力计算值与文献[30]中TA31钛合金球壳模型试验值较好吻合，预报误差不到1%，预报精度有一定提升，相比于双线性弹塑性简化模型，Bonora 材料本构关系模型充分考虑了材料屈服强度、抗拉强度以及最大塑性应变的影响，结构破坏的物理意义更加明确。

表3 计算结果汇总Tab.3 Calculation results

图11 基于理想弹塑性模型的球壳结构载荷位移曲线Fig.11 The load-displacement curve of spherical shell based on ideal elastic-plastic model

6 结 论

本文基于连续介质损伤力学理论框架，针对TA31 钛合金开展了Bonora 模型适用性研究，分析了典型耐压球壳结构的失效模式和极限承载能力，得出如下结论：

（1）本文设计并开展了钛合金标准试样的加载卸载试验，获得了材料损伤因子随塑性应变的变化规律，但试验测得的塑性应变与损伤因子均是标距范围内的平均值，不同截面的损伤缺陷分布是不均匀的，最小截面中心位置的塑性应变是试验平均值的2.8 倍，表明基于杨氏模量衰减的试验方法测得的损伤因子演化规律滞后于有限元方法计算得到的结果，加载卸载试验仅能反应损伤变量的演化趋势，无法准确测定最终的损伤临界值。

（2）未考虑损伤因素的J-C 塑性硬化模型在模拟标准试样单向拉伸时，会高估材料的硬化行为，无法准确模拟材料颈缩后的应力应变响应。Bonora损伤模型可以较准确地模拟材料软化行为和失效模式，模型中的主要参数分别为损伤起始塑性应变εˉth、临界失效塑性应变εˉcr、临界损伤因子Dcr和损伤指数α，基于本文提出的校准方法，在加载卸载试验的基础上，可以准确地获得上述模型参数。损伤指数α与材料内部孔洞缺陷的形核速率有关，α越大，材料内部孔洞扩张速率越快，材料塑韧性能越差；临界损伤因子Dcr=1 在数值仿真分析中具有明确物理意义，单元损伤因子趋近1 时，单元积分点有效应力趋于无穷大，能够模拟因缺陷演化而导致的应力集中现象。

（3）本文首次在耐压球壳极限强度分析中，引入了考虑损伤演化的Bonora 模型，可以准确模拟耐压球壳结构的失效模式和破坏压力，预报误差不足1%。该模型在材料本构关系中考虑了屈服强度、抗拉强度以及最大塑性应变的影响，对指导材料性能的优化与提升具有借鉴意义。但由于现阶段在公开发表的论文中，基于TA31 钛合金的球壳模型试验结果较少，单一模型不足以定量说明Bonora 模型的预报精度，后续工作会在此基础上针对性地开展重复试验，进一步消除试验分散度，提升Bonora模型的可靠性。

尽管Bonora 模型在应变能释放率中考虑了应力三轴度的影响，但本文尚未深入研究应力状态对损伤指数、损伤起始应变以及损伤临界应变的影响规律，因此下一步研究重点是考虑裂纹闭合效应和应力状态的Bonora模型适用性研究。